leetcode刷题---递归思想

1.1 递归介绍

如果在函数中存在着调用函数本身的情况，这种现象就叫递归。

递归的思想就是，将大问题分解为小问题来求解，然后再将小问题分解为更小的问题。这样一层层地分解，直到问题规模被分解得足够小，不用继续分解，可以直接计算结果为止。

如果把这个一层层分解的过程画成图，它其实就是一颗树，叫做递归树。以斐波那契数列为例子：

    def fib(n):if n <= 1:return 1return fib(n - 1 ) + fib(n - 2)

递归树如下图所示：

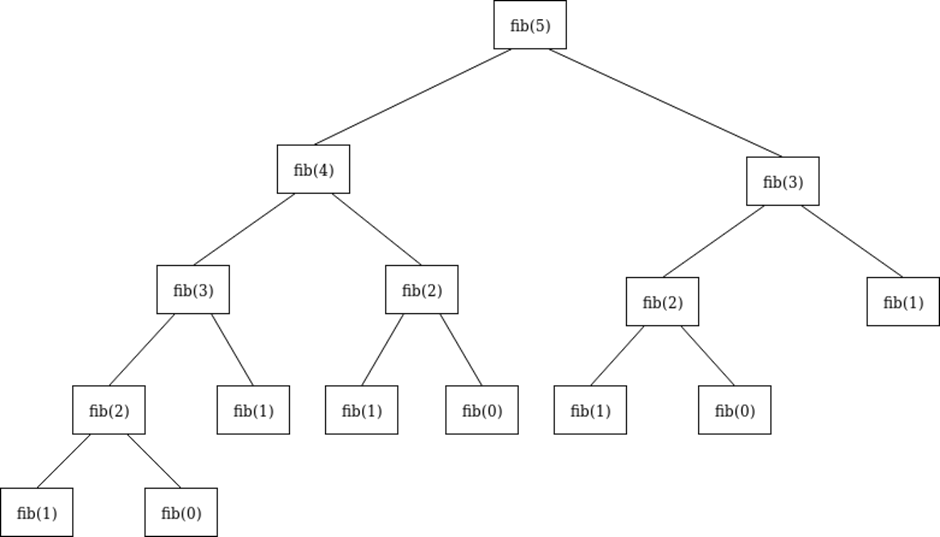
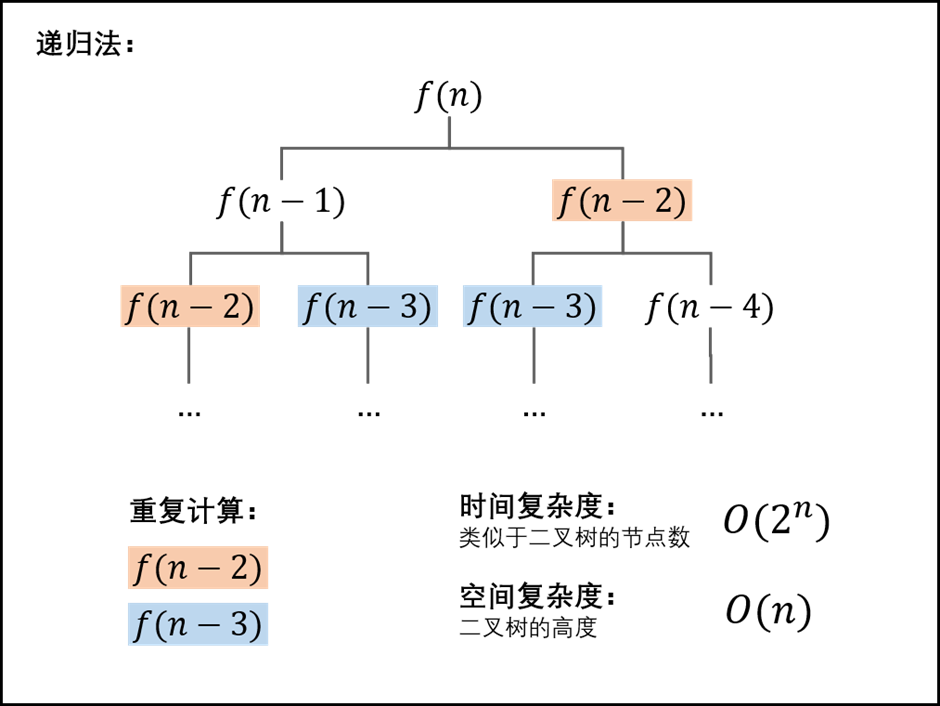
递归在“归”的过程中，符合后进先出的规则，所以需要用一个堆栈的数据结构。递归过程中函数调用会自动产生栈帧，当函数帧栈的深度越来越大的时候，栈也越来越大，如果递归没有终止条件，就会爆栈。所有基于递归思想实现的算法，第一步要思考的就是递归的终止条件。

进一步剖析「递归」，先有「递」再有「归」，「递」的意思是将问题拆解成子问题来解决， 子问题再拆解成子子问题，…，直到被拆解的子问题无需再拆分成更细的子问题（即可以求解），「归」是说最小的子问题解决了，那么它的上一层子问题也就解决了，上一层的子问题解决了，上上层子问题自然也就解决了。

递归的一般结构

    def func():if (符合边界条件)：return# 某种形式的调用func（）

1.2 基本步骤

（1） 定义一个函数，明确函数功能

（2） 寻找问题与子问题之间的关系（递推公式）

（3） 将递推公式在定义的函数中实现

（4） 推导时间复杂度，判定是否可以接受，无法接受更换算法

1.3 代表题目

1.3.1 入门题—青蛙跳

一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶，例如：
跳上第 1 级台阶只有一种跳法：直接跳 1 级即可。
跳上第 2 级台阶有两种跳法：每次跳 1 级，跳两次；或者一次跳 2 级。
问要跳上第 n 级台阶有多少种跳法？：

一只青蛙只能跳一步或两步台阶，自上而下地思考，也就是说如果要跳到 n 级台阶只能从 从 n-1 或 n-2 级跳 。那么从以上分析可得 f(n) = f(n-1) + f(n-2)，显然这就是我们要找的问题与子问题的关系，而显然当 n = 0, n = 1， 即跳一二级台阶是问题的最终解 。

递归解法：

def numWays(n):if n == 0 or n == 1:return 1return numWays(n - 1) + numWays(n - 2)时间复杂度高，因为在递归过程中有大量的重复计算。

优化1：空间换时间

def numWays(n):mid = [0] * (n + 1)if n == 0 or n == 1:return 1mid[0] = mid[1] = 1for i in range(2, n + 1):mid[i] = mid[i - 1] + mid[i - 2]return mid[n]空间换时间，时间复杂度O(n),空间复杂度O(n)

优化2：自下而上的方法

def numWays(n):if n == 0 or n == 1:return 1res = 0pre = 1next = 1for i in range(2, n + 1):res = pre + nextpre = nextnext = resreturn res时间复杂度O(n),空间复杂度O(1)

简单总结一下： 分析问题我们需要采用自上而下的思维，而解决问题有时候采用自下而上的方式能让算法性能得到极大提升，思路比结论重要 。

1.3.2.1 初级题

226.翻转二叉树

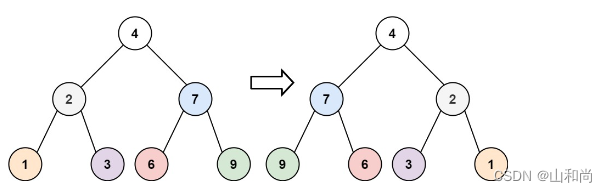
翻转(根节点) = 翻转(根节点的左节点) + 翻转(根节点的右节点) ，即 invert(root) = invert(root->left) + invert(root->right) ，递归的终止条件是当结点为叶子结点时终止（因为叶子节点没有左右结点） 。由于我们会对每一个节点都去做翻转，所以时间复杂度是 O(n)， 如果是完全二叉树，空间复杂度为树的高度O(logn) 。最坏情况，如果此二叉树只有左节点，没有右节点，则树的高度即结点的个数 n，此时空间复杂度为 O(n)，总的来看，空间复杂度为O(n) 。

def invertTree(self, root):# 叶子节点不能翻转if not root:return root# 翻转右节点下的左右节点right = self.invertTree(root.right)# 翻转左节点下的左右节点left = self.invertTree(root.left)# 左右节点下的二叉树翻转好后，翻转根节点的左右节点root.left = rightroot.right = leftreturn root

112.路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。说明: 叶子节点是指没有子节点的节点。示例: 
给定如下二叉树，以及目标和 sum = 22，5/ \4   8/   / \11  13  4/  \      \7    2      1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

是否存在一条路径，从当前节点root到叶子节点的路径和为sum，这个问题可以转化为：是否存在从当前节点的子节点到叶子的路径和为sum-子节点值。即：

hasPathSum(root,sum)=hasPathSum(root.left,sum-root.val) or hasPathSum(root.right,sum-root.val)

递归终止条件是当前节点是叶子节点，直接判断sum是否等于节点值即可。

def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:if not root:return Falseif not root.left and not root.right:return targetSum == root.valreturn self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)

1.3.3 中级题—汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。你需要原地修改栈。

将n个圆盘经由B移到C上，可以按照以下三个步骤来分析，首先将A上面的n-1个圆盘看成是一个圆盘：

1. 将A上面的n-1个圆盘经由C移到B
2. 将A底下最大的圆盘移到C
3. 再将B上的n-1个圆盘经由A移到C上

move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C)

终止条件我们很容易看出，当 A 上面的圆盘只有一个的时候。

# 将 n 个圆盘从 a 经由 b 移动到 c 上
def hanota(A, B, C):n = len(A)move(n, A, B, C)def move(n, A, B, C):if n == 1:C.append(A.pop())return# 将A上面的n-1个圆盘经由C移动到Bmove(n-1, A, C, B)# 将A底下最大的那块移动到CC.append(A.pop())# 将B上的n-1个圆盘经由A移动到Cmove(n - 1, B, A, C)

1.3.4 进阶题—细胞分裂