车道线检测-Eigenlanes 论文学习笔记
论文:《Eigenlanes: Data-Driven Lane Descriptors for Structurally Diverse Lanes》
代码:https://github.com/dongkwonjin/Eigenlanes
核心:在 Eigenlane Space 中检测车道线
创新点
- Eigenlane:数据驱动的车道描述符,在特征车道空间中紧凑地表示结构多样化的车道;
- SIIC-Net:高效地检测和回归特征车道空间中的道路车道;
- SDLane数据集:比现有数据集更真实地表示真实驾驶环境中结构多样化和复杂的车道;
0、结构

1、Eigenlanes
用车道线在训练集中的分布来表示车道线。
- 车道线:x=[x1,x2,...,xN]T\pmb{x}=[x_1,x_2,...,x_N]^Tx=[x1,x2,...,xN]T (横坐标)
- 车道线矩阵:A=[x1,x2,...,xL]\pmb{A}=[\pmb{x}_1,\pmb{x}_2,...,\pmb{x}_L]A=[x1,x2,...,xL](训练集中的所有车道线)
- 使用 Frobenius 泛数 ∣∣A−AM∣∣F||\pmb{A}-\pmb{A}_M||_F∣∣A−AM∣∣F ,其在被最小化时,A\pmb{A}A 的最佳 MMM 阶逼近为:
AM=[x~1,x~2,...,x~L]=σ1u1v1T+⋯+σMuMvMT\pmb{A}_M=[\pmb{\tilde{x}}_1,\pmb{\tilde{x}}_2,...,\pmb{\tilde{x}}_L]=\sigma_1 \pmb{u}_1 \pmb{v}^T_1+\cdots+\sigma_M \pmb{u}_M \pmb{v}^T_MAM=[x~1,x~2,...,x~L]=σ1u1v1T+⋯+σMuMvMT
其中:- UM=[u1,...,uM]\pmb{U}_M=[\pmb{u}_1,...,\pmb{u}_M]UM=[u1,...,uM] 是 U=[u1,...,uN]\pmb{U}=[\pmb{u}_1,...,\pmb{u}_N]U=[u1,...,uN] 的前 M 个左奇异向量;
- VM=[v1,...,vM]\pmb{V}_M=[\pmb{v}_1,...,\pmb{v}_M]VM=[v1,...,vM] 是 V=[v1,...,vL]\pmb{V}=[\pmb{v}_1,...,\pmb{v}_L]V=[v1,...,vL] 的前 M 个右奇异向量;
- ΣM=[σ1,...,σM]\pmb{\Sigma}_M=[\pmb{\sigma}_1,...,\pmb{\sigma}_M]ΣM=[σ1,...,σM] 是 Σ\pmb{\Sigma}Σ 的前 M 个奇异值(Σ\pmb{\Sigma}Σ 中的奇异值经过了由大到小的排序,均大于0,且最小值为 σr\sigma_rσr,r 是 A 的秩);
- U\pmb{U}U、V\pmb{V}V 以及 Σ\pmb{\Sigma}Σ 是通过奇异值分解 A=UΣV\pmb{A}=\pmb{U}\pmb{\Sigma}\pmb{V}A=UΣV 得到的。
- 由此可知:
- x~i=UMci=[u1,...,uM]ci\tilde{x}_i=\pmb{U}_M \pmb{c}_i=[\pmb{u}_1,...,\pmb{u}_M]\pmb{c}_ix~i=UMci=[u1,...,uM]ci
- 定义 Eigenlanes:u1,...,uM\pmb{u}_1,...,\pmb{u}_Mu1,...,uM
- 定义 Eigenlanes 空间:由 {u1,...,uM}\{\pmb{u}_1,...,\pmb{u}_M\}{u1,...,uM} 张成的空间
- 给定车道线 x\pmb{x}x,将其映射到 Eigenlanes 空间:x~=UMc\tilde{\pmb{x}}=\pmb{U}_M \pmb{c}x~=UMc,其中 c=UMTx\pmb{c}=\pmb{U}_M^T \pmb{x}c=UMTx
在 Eigenlanes 空间生成候选车道线
在低维空间进行聚类,效果更佳。

Algorithm 1 Lane candidate generation in eigenlane space
Input: Set of training lanes {x1,x2,...,xL}\{x_1,x_2,...,x_L\}{x1,x2,...,xL}, M=#M=\#M=# of eigenlanes, K=#K=\#K=# of lane candidates
- Construct the lane matrix A and perform SVD in A=UΣV\pmb{A}=\pmb{U}\pmb{\Sigma}\pmb{V}A=UΣV;
- Transform each lane xix_ixi to cic_ici via c=UMTx\pmb{c}=\pmb{U}_M^T \pmb{x}c=UMTx;
- Apply the K-means algorithm to {c1,c2,...,cL}\{c_1,c_2,...,c_L\}{c1,c2,...,cL} to obtain K centroids c1,c2,...,cKc^1,c^2,...,c^Kc1,c2,...,cK
- Generate the lane candidate lk=UMck\pmb{l}_k=\pmb{U}_M\pmb{c}^klk=UMck by inversely transforming each centroid ck\pmb{c}^kck
Output: Set of lane candidates {l1,...,lK}\{l_1,...,l_K\}{l1,...,lK}
在 Eigenlanes 空间上,(通过最近邻)检测到 l=UMc\pmb{l}=\pmb{U}_M\pmb{c}l=UMc 之后,再用一个回归器回归出 Δc\Delta \pmb{c}Δc,这样有:
l+Δl=UM(c+Δc)\pmb{l}+\Delta\pmb{l}=\pmb{U}_M(\pmb{c}+\Delta \pmb{c}) l+Δl=UM(c+Δc)


2、SIIC-Net
整体结构

Encoder:ResNet50
Decoder:Binary Segmentation Map
2.1、SI 模块(Self-lane Identification)
预测:车道线概率、位置偏移、最顶处点的高度
输入:Squeezed Feature Map XsX_sXs、候选车道线 lkl_klk
输出:P=σ(f1(Y)),H=σ(f2(Y)),O=f3(Y)P=\sigma(f_1(Y)),\ H=\sigma(f_2(Y)),\ O=f_3(Y)P=σ(f1(Y)), H=σ(f2(Y)), O=f3(Y)
其中,Ys=[Ys1,Ys2,...,YsC2]∈RK×C2Y_s=[Y^1_s,Y^2_s,...,Y^{C_2}_s]\in \mathbb{R}^{K\times C_2}Ys=[Ys1,Ys2,...,YsC2]∈RK×C2 是沿着候选车道线 lk\pmb{l}_klk 做均值:
Ysc=1∣lk∣Σp∈lkXsc(p)Y_s^c=\frac{1}{|\pmb{l}_k|}\Sigma_{p\in \pmb{l}_k}X^c_s(p) Ysc=∣lk∣1Σp∈lkXsc(p)
fif_ifi 分别是 C2×2C_2\times 2C2×2、C2×RC_2\times RC2×R、C2×MC_2\times MC2×M 的全连接层。OkO_kOk 就是前面提到的偏移量 Δck\Delta c_kΔck
SI 模块之后,应用 NMS T 次,以选出 T 条有价值的车道线。
2.2、IC 模块(Inter-lane Correlation)
利用了车道线之间的 相关性:
- 相邻车道等间距
- 透视变换下,车道线交于 Vanishing Point
输入:Aggregated Feature Map XaX_aXa、候选车道线 lkl_klk、前段 NMS 输出的 T 条车道线;
输出:相应两条车道线对的匹配度 R=ϕ1(Ya)×ϕ2(Ya)TR=\phi_1(Y_a)\times\phi_2(Y_a)^TR=ϕ1(Ya)×ϕ2(Ya)T
其中,
- YaY_aYa 使用 XaX_aXa 计算得到,计算方式与 YsY_sYs 类似,它是 T×C1T\times C_1T×C1 的矩阵
- RRR 是 T×TT\times TT×T 的矩阵,Rij∈[−1,1]R_{ij}\in [-1,1]Rij∈[−1,1]
- ϕ1\phi_1ϕ1 与 ϕ2\phi_2ϕ2 是用卷积与 l2l_2l2 泛数实现的特征变换。
2.3、MWCS 模块
这是一种图优化技术,可见论文:《Harmonious Semantic Line Detection via Maximal Weight Clique Selection》
主要有两步操作:
- 寻找可以修正的最佳车道线 clique;
- 通过删除 y 坐标比 HviH_{v_i}Hvi 大的点,修正了每条车道线的高度;(后面不再赘述)
寻找可以修正的最佳车道线 clique
构建完全图
- G=(V,E)G=(\mathcal{V},\mathcal{E})G=(V,E)
- V={v1,v2,...,vT}\mathcal{V}=\{v_1,v_2,...,v_T\}V={v1,v2,...,vT} 是 NMS 输出的车道线
- E={(vi,vj):i≠j}\mathcal{E}=\{(v_i,v_j):i\ne j\}E={(vi,vj):i=j},每条边上有个权重 w(vi,vj)=12(Rij+Rji)w(v_i,v_j)=\frac{1}{2}(R_{ij}+R_{ji})w(vi,vj)=21(Rij+Rji)
定义匹配度
- 记 θ\thetaθ 为车道线 clique,由图节点的序号构成;
- θ\thetaθ 上的匹配度 Ecompatible(θ)E_{compatible}(\theta)Ecompatible(θ):
Ecompatible(θ)=Σi∈θΣj∈θ,j>iw(vi,vj)E_{compatible}(\theta)=\Sigma_{i\in\theta}\Sigma_{j\in\theta,j>i}w(v_i,v_j) Ecompatible(θ)=Σi∈θΣj∈θ,j>iw(vi,vj)
选 clique θ∗\theta^*θ∗
θ∗=argmaxθEcompatible(θ)\theta^*=\arg\max_\theta E_{compatible}(\theta) θ∗=argθmaxEcompatible(θ)
其中,限定 w(vi,vj)>κw(v_i,v_j)>\kappaw(vi,vj)>κ。
如果没有满足约束的 clique,则选择最大的单节点 clique:θ∗={i∗}\theta^*=\{i^*\}θ∗={i∗},其中 i∗=argmaxiPvii^*=\arg\max_i P_{v_i}i∗=argmaxiPvi
调整候选车道线
使用 U(cvi+Δcvi)\pmb{U}(\pmb{c_{v_i}}+\Delta\pmb{c_{v_i}})U(cvi+Δcvi) 调整 θ∗\theta^*θ∗ 中的车道线,其中 Δcvi\Delta\pmb{c_{v_i}}Δcvi 是 SI 模块的输出。
相关文章:

车道线检测-Eigenlanes 论文学习笔记
论文:《Eigenlanes: Data-Driven Lane Descriptors for Structurally Diverse Lanes》 代码:https://github.com/dongkwonjin/Eigenlanes 核心:在 Eigenlane Space 中检测车道线 创新点 Eigenlane:数据驱动的车道描述符ÿ…...

docker run mysql -e 的环境变量 Environment Variables
例子 sudo docker run -itd --name DockerMysqlLatest3307 -p 3307:3306 -e MYSQL_ROOT_PASSWORDroot的密码 mysql:latest### root无密码 sudo docker run -itd --name Mysql57 -p 57:3306 -e MYSQL_ALLOW_EMPTY_PASSWORDroot mysql:5.7https://hub.docker.com/_/mysql?tabde…...

第17章 MongoDB 条件操作符教程
第17章 MongoDB 条件操作符教程 描述 条件操作符用于比较两个表达式并从mongoDB集合中获取数据。 在本章节中,咱们将讨论如何在MongoDB中使用条件操作符。 MongoDB中条件操作符有: (>) 大于 - $gt(<) 小于 - $lt(>) 大于等于 - $gte(< …...
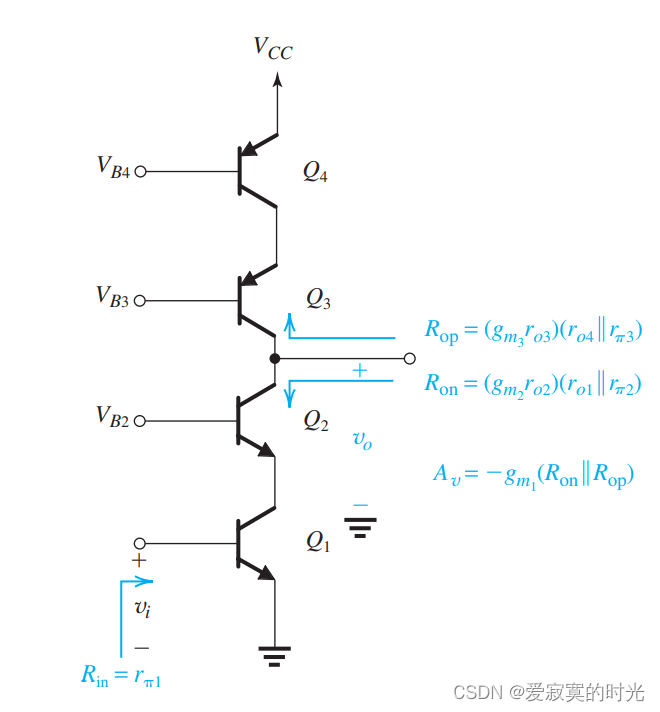
电子技术——共源共栅放大器
电子技术——共源共栅放大器 之前我们提到过,提高基础增益单元(共源放大器)的一种方法是提高其 ror_oro 的阻值,之后我们学过共栅放大器作为电流缓冲器可以做到这一点,自然地我们就得到了终极解决方案,也…...
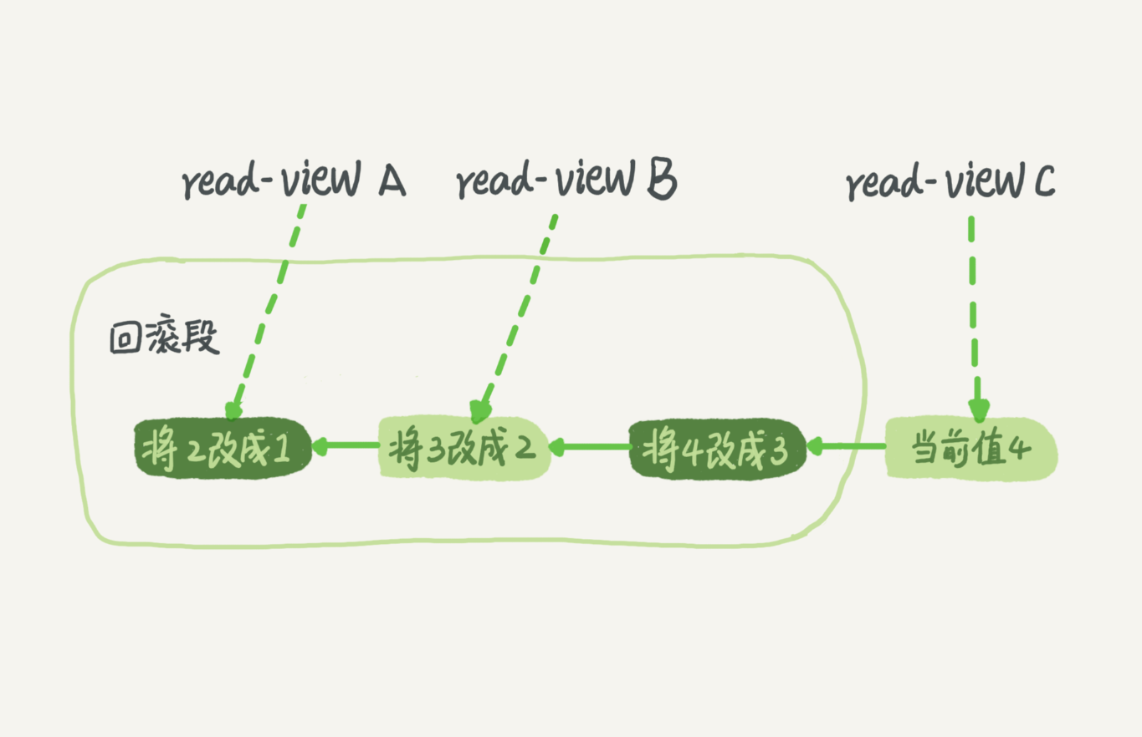
《MySQL学习》 事务隔离 与 MVCC
《MySQL学习》 事务隔离 一.事务的概念 事务保证一组数据要么全部成功要么全部失败,MySQL的事务基于引擎(如InnoDB)实现。 二.事务的隔离性与隔离级别 MySQL的标准隔离级别: 读未提交 : 一个事务还没提交时&#…...
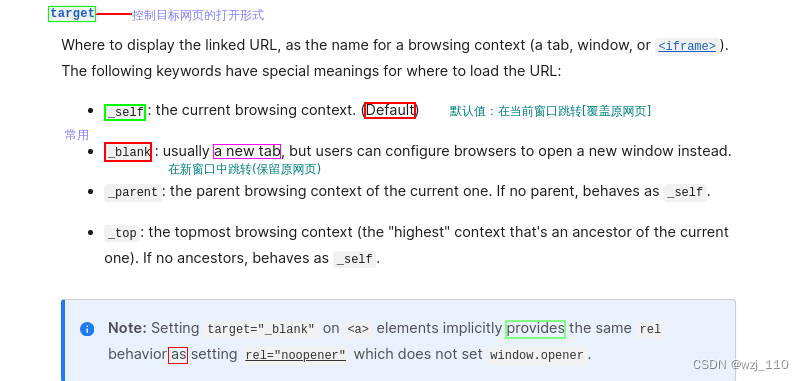
html(二)基础标签
一 HTML中的注释 重点: 在哪写注释? 注释的形式? vs code和webstorm都可以通过 ctrl / 进行单行注释和取消注释 ① html中注释的形式 1) html文档中单行和多行注释是"<!-- -->" -->html2) 在html文档中,script标签…...
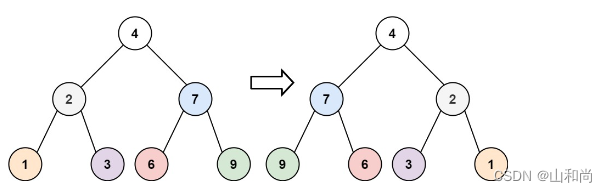
leetcode刷题---递归思想
leetcode刷题---递归思想)1.1 递归介绍1.2 基本步骤1.3 代表题目1.3.1 入门题---青蛙跳1.3.2.1 初级题226.翻转二叉树112.路径总和1.3.3 中级题---汉诺塔问题1.3.4 进阶题---细胞分裂1.1 递归介绍 如果在函数中存在着调用函数本身的情况,这种现象就叫递…...
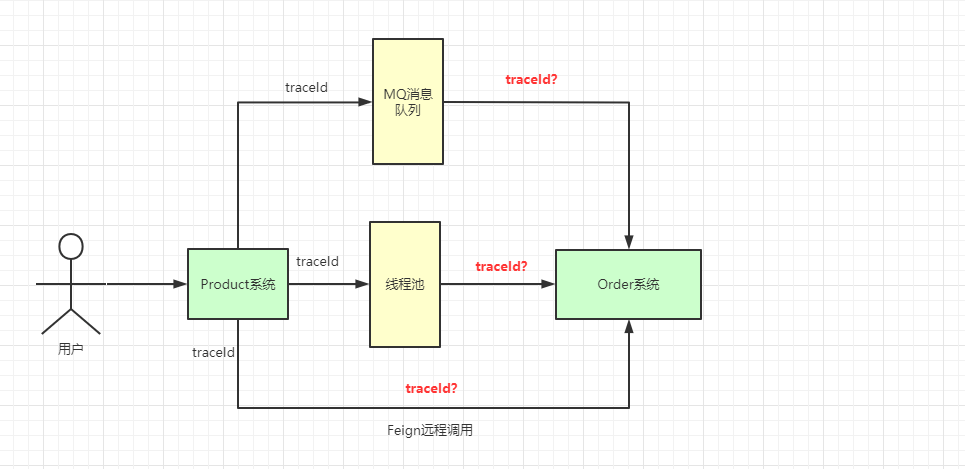
ThreadLocal 源码级别详解
ThreadLocal简介 稍微翻译一下: ThreadLocal提供线程局部变量。这些变量与正常的变量不同,因为每一个线程在访问ThreadLocal实例的时候(通过其get或set方法)都有自己的、独立初始化的变量副本。ThreadLocal实例通常是类中的私有静…...

训练营day17
110.平衡二叉树 力扣题目链接 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。 示例 1: 给定二叉树 [3,9,20,null,null,15,7] 返回 true 。 示…...
Nodejs原型链污染
Nodejs与JavaScript和JSON 有一些人在学习JavaScript时会分不清Nodejs和JavaScript之间的区别,如果没有node,那么我们的JavaScript代码则由浏览器中的JavaScript解析器进行解析。几乎所有的浏览器都配备了JavaScript的解析功能(最出名的就是…...

【Vue3】element-plus中el-tree的递归处理赋值回显问题
目录一:先获取所有权限tree二:在获取所有该角色能有的权限tree三:递归处理勾选tree节点由于项目是从0-1开始构建的 rbac都需要重新构建对接 所以涉及到了权限管理和菜单管理 一级菜单包含多个二级菜单 若二级不全选,则一级显示 半…...

C语言---宏
专栏:C语言 个人主页:HaiFan. 专栏简介:本专栏主要更新一些C语言的基础知识,也会实现一些小游戏和通讯录,学时管理系统之类的,有兴趣的朋友可以关注一下。 #define预处理预定义符号define#define定义标识符…...

算法导论—路径算法总结
图算法 单源最短路径 Bellman-Ford算法: 顶点为V,边为E的图 对每条边松弛|V|-1次边权可以为负值若存在一个可以从源结点到达的权值为负值的环路,算法返回False时间复杂度:O(VE) 有向无环图单源最短路径 DAG-SHORTEST-PATHS …...

程序环境--翻译+执行
ANSI C标准下,有两种程序环境。 第1种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。 翻译环境包括:预处理(预编译)编译汇编链接。四个步骤。 第2种是执行/运行环境,它用于实际执行代码。 链接…...

微信小程序内部那些事
微信小程序没有window、document,它更像是一个类似 Node.js 的宿主环境。因此在小程序内部不能使用 document.querySelector 这样的选择器,也不支持 XMLHttpRequest、location、localStorage 等浏览器 API,只能使用小程序自己提供的 API&…...

这是从零在独自开开发,将是副业赚钱最好的平台!
文章目录最重要的事情放前面1.前言2.简单介绍一下3.【独自开】介绍3.1 分层标准化平台架构3.2 集成第三方数字接口3.3 支持各个行业的系统定制开发4.如何在【独自开】赚钱获取收益?4.1 如何称为【独自开】开发者?最重要的事情放前面 通过平台的审核也可以得到相应的奖金&…...

Spring MVC 之获取参数(对象、JSON格式数据、URL地址参数、文件、Cookie)
文章目录1. 获取单个参数2. 获取多个参数3. 获取对象4. 后端参数重命名 RequestParam5. 接收 JSON 格式的数据 RequestBody6. 从 URL 地址中获取参数 PathVariable7. 上传文件 RequestPart8. 获取Cookie (CookieValue)/Session/header8.1 获取 Request 和 Response 对象8.2 获取…...

永磁同步电机中BEMF电阻的作用
一、电路原理图 二、原理分析 如图一我们测的是相电压,从理论上我们知道我们测得相电压是一个马鞍波形,马鞍波形中并没有隐含 转子的位置和速度信息。那么为什么我们还要有这样一个电路呢? 这个问题其实困惑了我好久?直到有一天…...

JAVA练习45-二叉树的层序遍历
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目二叉树的层序遍历 …...

超高精度PID调节器的特殊功能(3)——变送输出(转发)功能及其应用
摘要:变送输出是高级PID控制器的一项重要扩展功能,可用于多区控制、串级控制、比值控制和差值控制以及数据采集及记录。为展示变送输出功能的强大作用,本文主要针对超高精度VPC 2021系列PID控制器,介绍了变送输出的具体功能、参数…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
