6.开源非对称加密算法SM2实现
6.开源非对称加密算法SM2实现
前期内容导读:
- 开源加解密RSA/AES/SHA1/PGP/SM2/SM3/SM4介绍
- 开源AES/SM4/3DES对称加密算法介绍及其实现
- 开源AES/SM4/3DES对称加密算法的验证实现
- 开源非对称加密算法RSA/SM2实现及其应用
- 开源非对称加密算法RSA实现
1. 开源组件 非对称秘钥加密介绍
- 加密组件引入方法:
<dependency><groupId>com.biuqu</groupId><artifactId>bq-encryptor</artifactId><version>1.0.1</version> </dependency>
1.1 SM2的加解密实现
- 加解密核心逻辑
public byte[] doCipher(byte[] data, byte[] key, int cipherMode) {SM2Engine.Mode mode = SM2Engine.Mode.C1C2C3;if (!this.getPaddingMode().equalsIgnoreCase(String.valueOf(DEFAULT_MODE))){mode = SM2Engine.Mode.C1C3C2;}SM2Engine sm2Engine = new SM2Engine(mode);this.initSm2Engine(sm2Engine, key, cipherMode);try{return sm2Engine.processBlock(data, 0, data.length);}catch (Exception e){throw new EncryptionException("failed to do sm2 cipher.", e);} }private void initSm2Engine(SM2Engine sm2Engine, byte[] key, int cipherMode) {if (Cipher.ENCRYPT_MODE == cipherMode){ECPublicKey keyObj = (ECPublicKey)this.toPubKey(key);ECDomainParameters domainParam = this.getDomainParam(keyObj);ECKeyParameters keyParam = new ECPublicKeyParameters(keyObj.getQ(), domainParam);byte[] initKey = UUID.randomUUID().toString().getBytes(StandardCharsets.UTF_8);sm2Engine.init(true, new ParametersWithRandom(keyParam, this.createRandom(initKey)));}else{ECPrivateKey keyObj = (ECPrivateKey)this.toPriKey(key);ECDomainParameters domainParam = this.getDomainParam(keyObj);ECKeyParameters keyParam = new ECPrivateKeyParameters(keyObj.getD(), domainParam);sm2Engine.init(false, keyParam);} }说明:
- 上面的代码阐述了加解密的核心流程:根据二进制生成秘钥,再基于单独的API计算得到加解密结果,该计算逻辑完全不同于以往的加解密API;
- 通过上述核心代码逻辑,再对比上篇5.非对称加密算法RSA实现,可知SM2本身是支持分段的;
- 通过秘钥二进制反向生成秘钥对象是一个有意思且有点复杂的事情,后面再单独说明;
1.2 SM2生成秘钥及转换实现
-
秘钥生成逻辑
public KeyPair createKey(byte[] initKey) {try{ECGenParameterSpec paramSpec = new ECGenParameterSpec(SM2_VERSION);KeyPairGenerator keyGen = KeyPairGenerator.getInstance(ALGORITHM, this.getProvider());if (null == initKey){initKey = UUID.randomUUID().toString().getBytes(StandardCharsets.UTF_8);}SecureRandom random = this.createRandom(initKey);keyGen.initialize(paramSpec, random);return keyGen.generateKeyPair();}catch (Exception e){throw new EncryptionException("failed to get sm2 key.", e);} } -
公钥、私钥反向生成逻辑
public PublicKey toPubKey(byte[] pubKey) {try{String hexKey = Hex.toHexString(pubKey);KeyFactory kf = KeyFactory.getInstance(ALGORITHM, this.getProvider());if (hexKey.startsWith(STANDARD_HEX_KEY_PREFIX)){return kf.generatePublic(new X509EncodedKeySpec(pubKey));}else{// 获取SM2相关参数X9ECParameters ecParam = GMNamedCurves.getByName(SM2_VERSION);// 将公钥HEX字符串转换为椭圆曲线对应的点ECCurve ecCurve = ecParam.getCurve();ECPoint ecPoint = ecCurve.decodePoint(pubKey);// 椭圆曲线参数规格ECParameterSpec ecSpec = new ECParameterSpec(ecCurve, ecParam.getG(), ecParam.getN(), ecParam.getH());// 将椭圆曲线点转为公钥KEY对象return kf.generatePublic(new ECPublicKeySpec(ecPoint, ecSpec));}}catch (Exception e){throw new EncryptionException("failed to get sm2 pub key.", e);} }public PrivateKey toPriKey(byte[] priKey) {try{String hexKey = Hex.toHexString(priKey);KeyFactory kf = KeyFactory.getInstance(ALGORITHM, this.getProvider());if (hexKey.startsWith(STANDARD_HEX_KEY_PREFIX)){PKCS8EncodedKeySpec keySpec = new PKCS8EncodedKeySpec(priKey);return kf.generatePrivate(keySpec);}else{// 获取SM2相关参数X9ECParameters ecParam = GMNamedCurves.getByName(SM2_VERSION);ECCurve ecCurve = ecParam.getCurve();// 椭圆曲线参数规格ECParameterSpec ecSpec = new ECParameterSpec(ecCurve, ecParam.getG(), ecParam.getN(), ecParam.getH());// 将私钥HEX字符串转换为16进制的数字值BigInteger bigInteger = new BigInteger(Hex.toHexString(priKey), EncryptionConst.HEX_UNIT);// 将X值转为私钥KEY对象return kf.generatePrivate(new ECPrivateKeySpec(bigInteger, ecSpec));}}catch (Exception e){throw new EncryptionException("failed to get sm2 pri key.", e);} }说明:SM2基于椭圆的原理来加解密,其秘钥生成和解析方式也与其它方式不同。
- SM2支持标准的秘钥生成方式:
BaseSingleSignature sm2 = new Sm2Encryption(); KeyPair keyPair = sm2.createKey(UUID.randomUUID().toString().getBytes(StandardCharsets.UTF_8)); byte[] priKey0 = keyPair.getPrivate().getEncoded(); byte[] pubKey0 = keyPair.getPublic().getEncoded();- SM2支持非标准的秘钥生成方式:
BaseSingleSignature sm2 = new Sm2Encryption(); KeyPair keyPair = sm2.createKey(UUID.randomUUID().toString().getBytes(StandardCharsets.UTF_8)); byte[] priKey1 = ((BCECPrivateKey)keyPair.getPrivate()).getD().toByteArray(); byte[] pubKey1 = ((BCECPublicKey)keyPair.getPublic()).getQ().getEncoded(false); byte[] pubKey2 = ((BCECPublicKey)keyPair.getPublic()).getQ().getEncoded(true);- 上述正文部分的秘钥转换逻辑可以无感兼容上述各种秘钥场景。有兴趣可以看看此算法的单元测试类。PS:网上资料通常只描述了其中一种秘钥生成场景,但是相互间是不兼容的。
-
签名和验签判定逻辑:
public byte[] sign(byte[] data, byte[] key) {try{PrivateKey priKey = this.toPriKey(key);Signature signature = Signature.getInstance(this.getSignatureAlg(), this.getProvider());signature.initSign(priKey);signature.update(data);return signature.sign();}catch (Exception e){throw new EncryptionException("failed to signature.", e);} }public boolean verify(byte[] data, byte[] key, byte[] sign) {try{PublicKey pubKey = this.toPubKey(key);Signature signature = Signature.getInstance(this.getSignatureAlg(), this.getProvider());signature.initVerify(pubKey);signature.update(data);return signature.verify(sign);}catch (Exception e){throw new EncryptionException("failed to verify signature.", e);} } -
SM2加密批量验证逻辑
@Test public void encrypt() {int[] encLengths = {256};super.encrypt(encLengths); }@Test public void testEncryptAndSign() {String initKey = UUID.randomUUID() + new String(RandomUtils.nextBytes(5000), StandardCharsets.UTF_8);int[] encLengths = {256};BaseSingleSignature encryption = new Sm2Encryption();for (int encLen : encLengths){encryption.setEncryptLen(encLen);KeyPair keyPair = encryption.createKey(initKey.getBytes(StandardCharsets.UTF_8));super.testEncryptAndSign(encryption, keyPair.getPrivate().getEncoded(), keyPair.getPublic().getEncoded());} }说明:
- SM2可以不用设置加密长度,因为默认只有一个,同理我们也无需关心其填充算法;
- 通过单元测试对比RSA算法可知,SM2由于秘钥非常短,其秘钥生成和加解密效率明显高于RSA;
2. 总结:
- 基于
BouncyCastle的SM2由于其算法独特性,与其它的算法实现差异加大,但是在实际使用时,由于其秘钥非常短,在核心的加解密执行效率上是有一定优势的; - SM2支持多种方式的秘钥生成,本开源组件较好地解决了秘钥不同方式生成的兼容问题;
- SM2算法相对来说还比较新,在有些
秘改(国密改造)场景时,还无法做到。因为大部分开源组件只支持标准协议,一般支持p256v1非对称加密,但是不支持sm2p256v1,国人仍需努力。
相关文章:

6.开源非对称加密算法SM2实现
6.开源非对称加密算法SM2实现 前期内容导读: 开源加解密RSA/AES/SHA1/PGP/SM2/SM3/SM4介绍开源AES/SM4/3DES对称加密算法介绍及其实现开源AES/SM4/3DES对称加密算法的验证实现开源非对称加密算法RSA/SM2实现及其应用开源非对称加密算法RSA实现 1. 开源组件 非对称秘…...
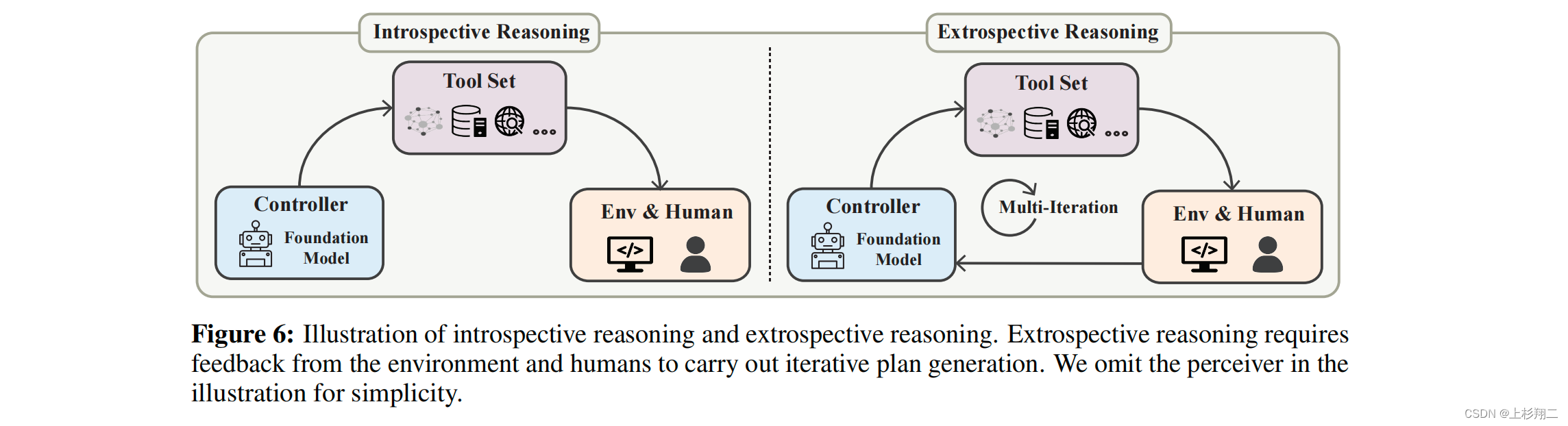
Toolformer and Tool Learning(LLMs如何使用工具)
大模型的能力让学术和工业界都对通用人工智能的未来充满幻想,在前一篇博文中已经粗略介绍, Augmented Language Models(增强语言模型) ALM的两大思路是推理和工具,本篇博文整理两篇关于Toolformer或Tool Learning的论…...

029:Mapbox GL绘制铁路黑白交替的线段
第029个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中加载数据显示铁路标识的那种黑白交替的线段。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共94行)相关API参考:专栏目标示例效果 配置方式 1)…...

结对编程 --- 大部分程序员喜欢的编程方式
一、介绍 结对编程起源时间可以追溯到 1990 年代早期。这种编程方法最初由 Jim Highsmith 和 Alistair Cockburn 等人提出。后来,Kent Beck 和 Ward Cunningham 等人将其发展成为一种敏捷开发方法,被称为“极限编程”(Extreme Programming&am…...
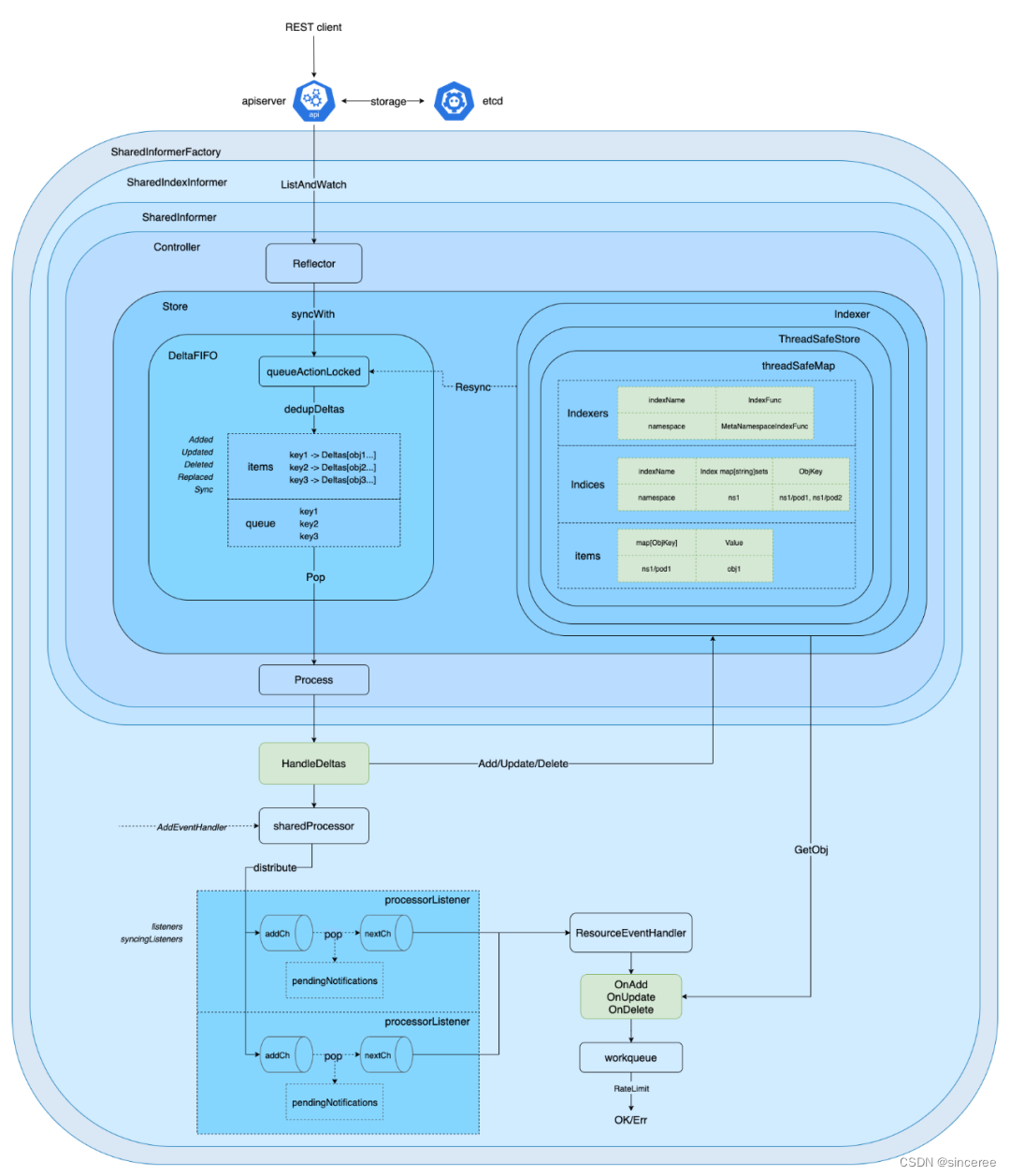
kubernetes-informer机制
一、概念 informer 是 client-go 中的核心工具包,在kubernetes中,各个组件通过HTTP协议跟 API Server 进行通信。如果各组件每次都直接和API Server 进行交互,会给API Server 和ETCD造成非常大的压力。在不依赖任何中间件的情况下࿰…...

LeetCode 2451. Odd String Difference【字符串,哈希表】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
切片工具tippecanoe的全网最详细的解释
1.下载和安装 tippecanoe工具是mapbox官方提供的一个服务端切片工具,因此它是运行在服务器上的,它比较友好的支持mac和linux机器。对于windows来讲,就比较麻烦了。 首先对于mac系统,你只需配置好自己的homebrew,保证homebrew能够正常下载东西。 然后只需要一个命令: …...
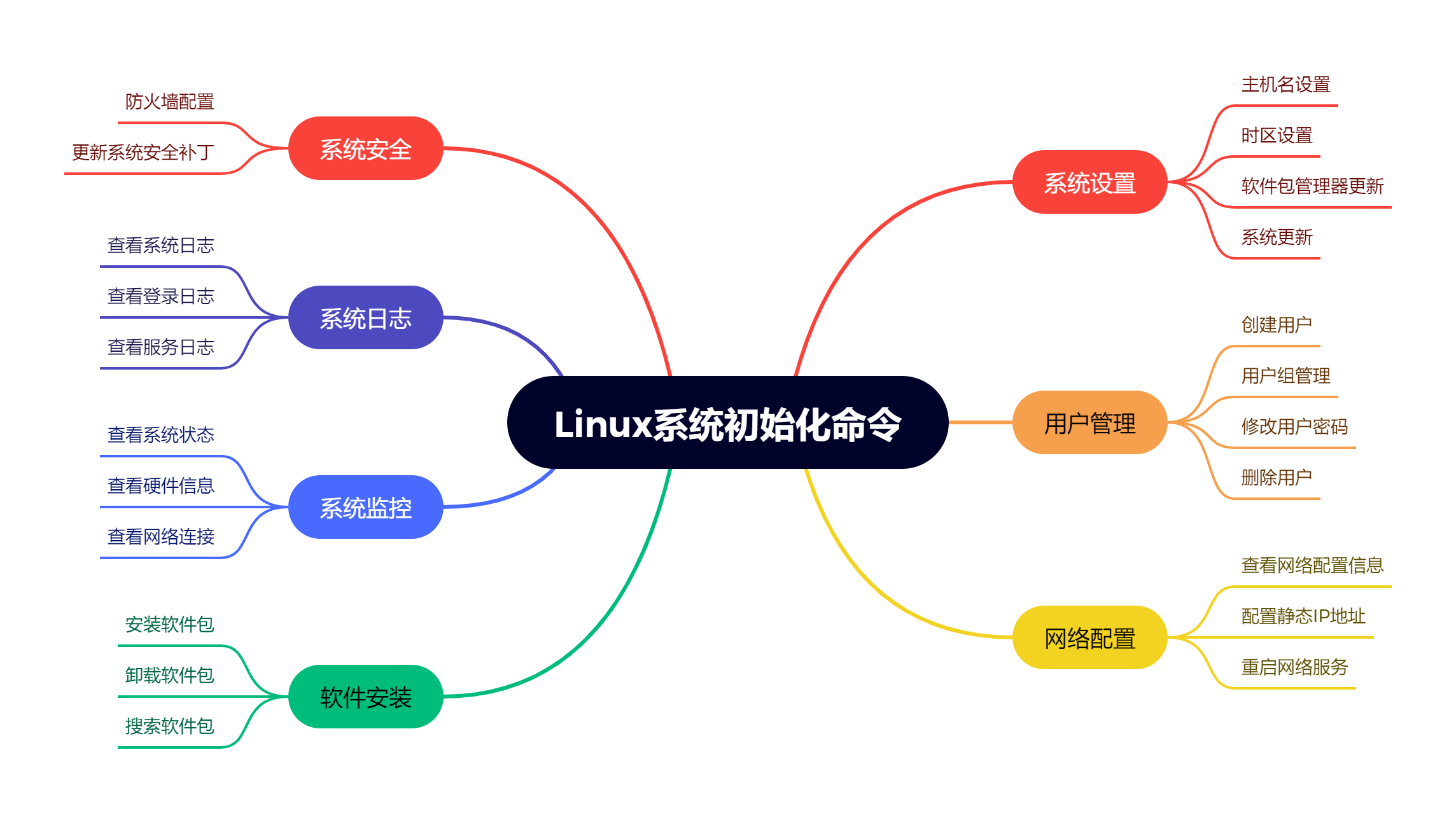
Linux系统初始化命令的备忘单,Linux运维工程师收藏!
在管理和维护Linux系统时,有一些常用的命令可以帮助您进行系统初始化和配置。这些命令涵盖了各种任务,包括系统设置、用户管理、软件安装和网络配置等。 本文将为您提供一个Linux系统初始化命令的备忘单,以便在需要时方便查阅和使用。 系统设…...

五月最近一次面试,被阿里P8测开虐惨了...
都说金三银四涨薪季,我是着急忙慌的准备简历——5年软件测试经验,可独立测试大型产品项目,熟悉项目测试流程...薪资要求?5年测试经验起码能要个20K吧 我加班肝了一页半简历,投出去一周,面试电话倒是不少&a…...
工业机器视觉缺陷检测工作小结
工业机器视觉检测工作小结 (因为网上没有很系统的讲义和文档,都是零零散散的,因此,我自己尝试着总结一下、仅供参考) 你想知道的大概率在这都可以找到、相机的了解镜头的了解光源的了解传统算法DL深度学习方法 &#…...

技术笔记:默默耕耘,赢得铁粉的秘密策略!
目录 第一步:真实实践,价值分享第二步:高质量文章的撰写第三步:积极互动,回复评论和留言第四步:定期更新和持续学习第五步:参与技术社区第六步:社区问答和问题解答总结 导语…...
回收站中怎么找回误删除的文件?这几种方法很实用
当我们在电脑上操作文件的时候,难免会有不小心删除文件的情况发生。这个时候,我们可以打开回收站来找回误删除的文件。但是,有时候我们也会误将回收站清空。那么,该怎样才能找回已经误删除的文件呢?在这里提供了回收站…...
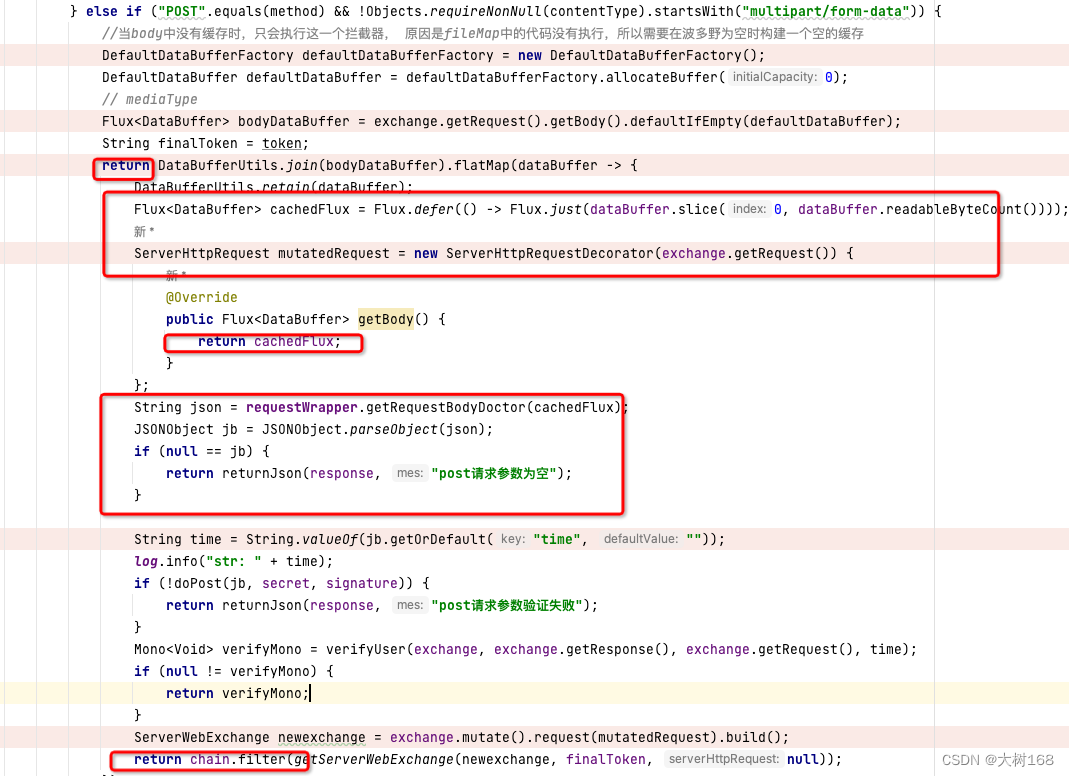
Gateway网关参数进行验签POST 包含requestbody 请求体封装
Gateway网关自定义拦截器的不可重复读取数据 特别注意一点, 因为在网关层 拿出 request 流之后,必须重写getbody()方法把所有的参数放进去,否则后面转发的请求无法接收到任何数据, 坑,巨坑,因为版本问题网上很多都不能兼容, 我的springboot环境 依赖包 <parent><gr…...
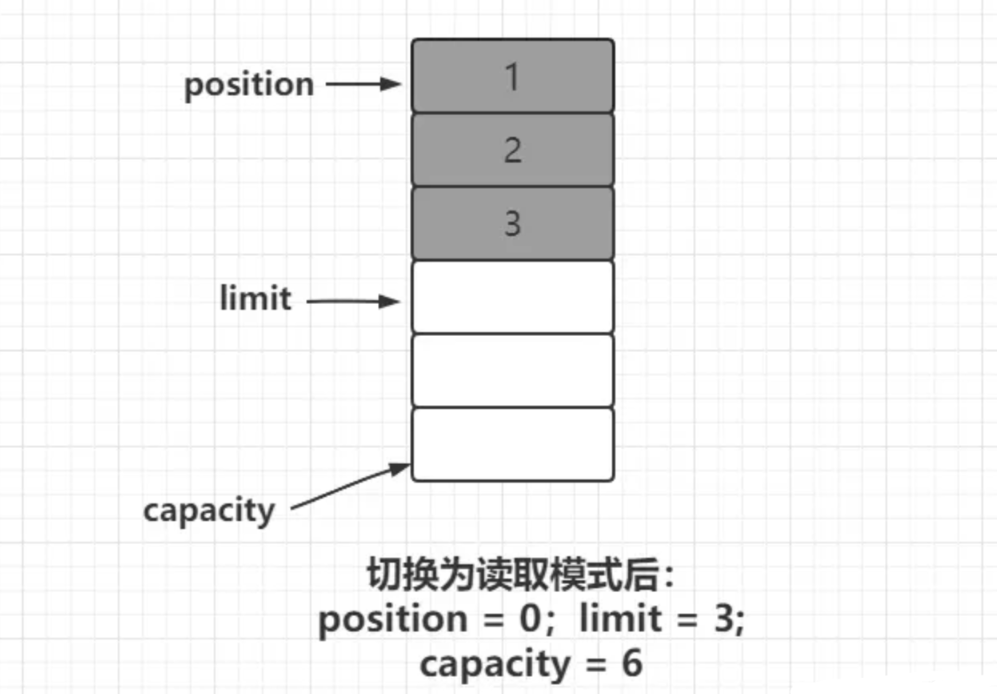
【Netty】字节缓冲区 ByteBuf (六)(上)
文章目录 前言一、ByteBuf类二、ByteBuffer 实现原理2.1 ByteBuffer 写入模式2.2 ByteBuffer 读取模式2.3 ByteBuffer 写入模式切换为读取模式2.4 clear() 与 compact() 方法2.5 ByteBuffer 使用案例 总结 前言 回顾Netty系列文章: Netty 概述(一&…...
Python - 面向对象编程 - 实例方法、静态方法、类方法
实例方法 在类中定义的方法默认都是实例方法,前面几篇文章已经大量使用到实例方法 实例方法栗子 class PoloBlog:def __init__(self, name, age):print("自动调用构造方法")self.name nameself.age agedef test(self):print("一个实例方法&…...
性能测试——基本性能监控系统使用
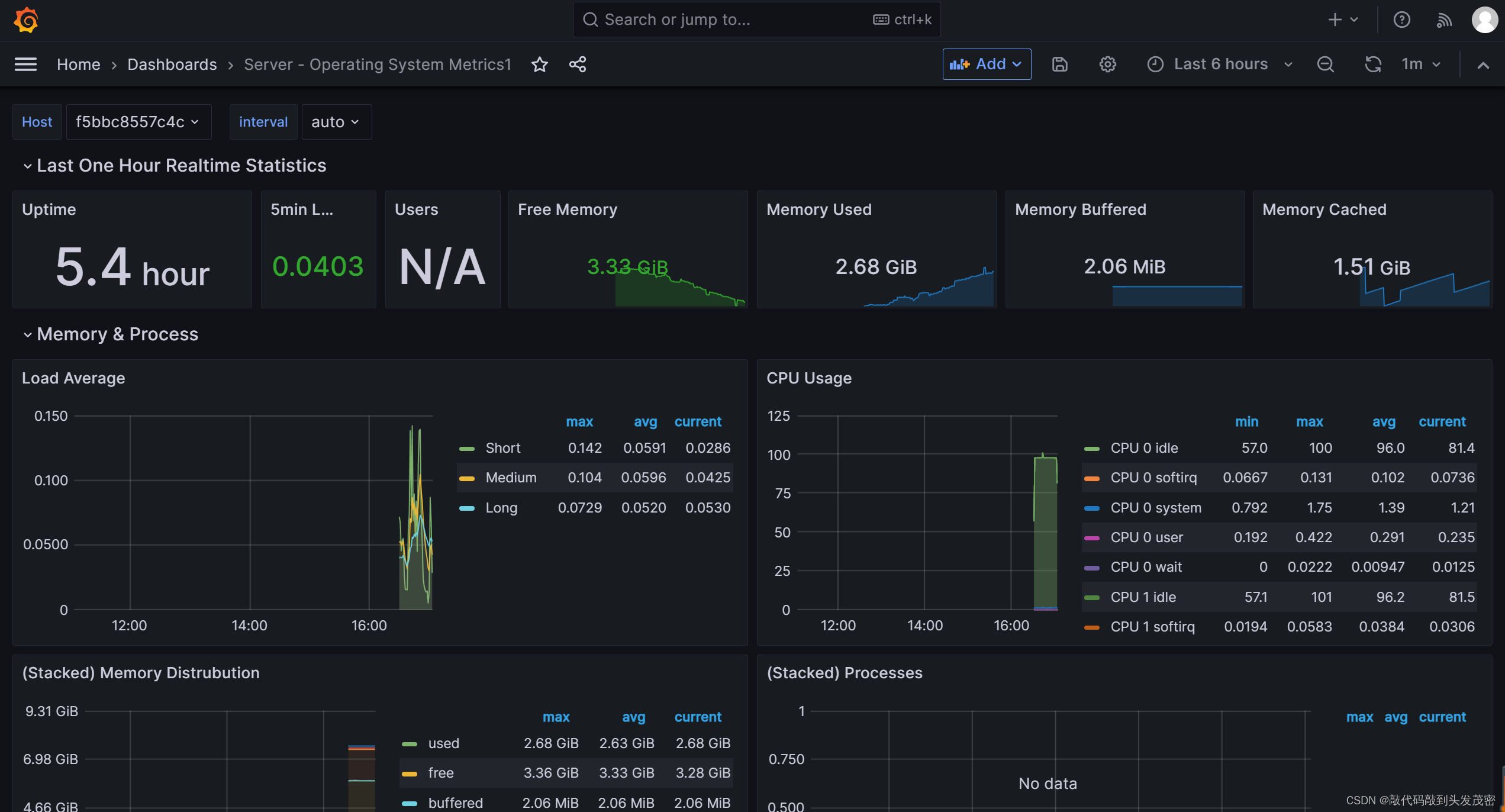
这里写目录标题 一、基本性能监控系统组成二、环境搭建1、准备数据文件 type.db collectd.conf2、启动InfluxDB3、启动grafana4、启动collectd5、Grafana中配置数据源 一、基本性能监控系统组成 Collectd InfluxdDB Grafana Collectd 是一个守护(daemon)进程,用来…...

JavaCollection集合
5 Collection集合 5.1 Collection集合概述 是单列集合的顶层接口,它表示一组对象,这些对象也称Collection元素JDK不提供此接口的直接实现,它提供更具体的子接口(Set 和 List)实现package ceshi;import java.util.AbstractCollection; import java.util.ArrayList; import…...

C++中string的用法
博主简介:Hello大家好呀,我是陈童学,一个与你一样正在慢慢前行的人。 博主主页:陈童学哦 所属专栏:CSTL 前言:Hello各位小伙伴们好!欢迎来到本专栏CSTL的学习,本专栏旨在帮助大家了解…...

目标检测YOLO实战应用案例100讲-基于深度学习的交通场景多尺度目标检测算法研究与应用
目录 基于深度学习的交通目标检测算法研究 传统的目标检测算法 基于深度学习的目标检测算法 </...

面试:vue事件绑定修饰符
stop - 调用 event.stopPropagation()。 prevent - 调用 event.preventDefault()。 trim 自动过滤用户输入的首尾空格 number 将输出字符串转为Number类型 enter 回车键 capture - 添加事件侦听器时使用 capture 模式。 self - 只当事件是从侦听器绑定的元素本身触发时才触发…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
