代码随想录算法训练营第四十五天 | 力扣 70. 爬楼梯(进阶), 322. 零钱兑换, 279.完全平方数
70. 爬楼梯(进阶)
题目
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
改为:一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢
解析
1阶,2阶,.... m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
1.确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
2.确定递推公式
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j]
3.dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
4.确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
5.举例来推导dp数组
略
Java代码实现
public int climbNStairs(int n,int m){int[] dp = new int[n + 1];dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (i - j > 0) {dp[i] += dp[i - j];}}}return dp[n];
}322. 零钱兑换
题目
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
解析
1.确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2.确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3.dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
4.确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
本题并不强调集合是组合还是排列。
采用coins放在外循环,target在内循环的方式。
遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
5.举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例
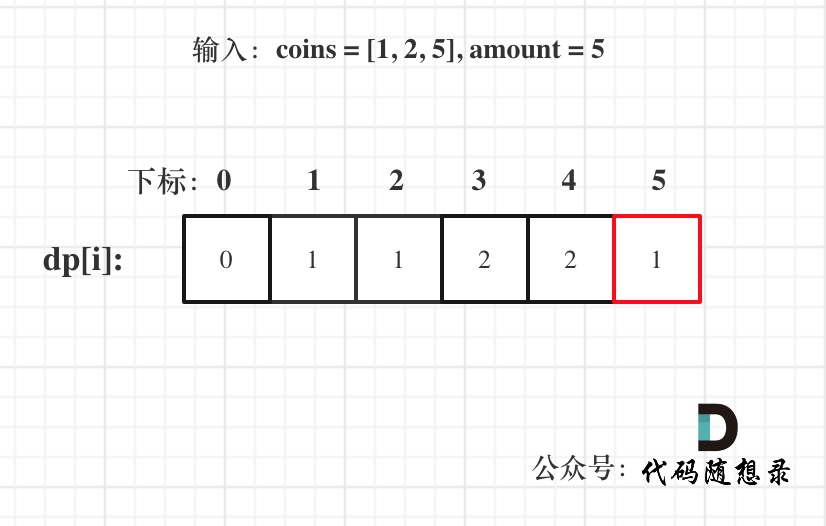
Java代码实现
public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];Arrays.fill(dp, max);dp[0] = 0;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {if (dp[j - coins[i]] != max) {dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];
}279.完全平方数
题目
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
解析
1.确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
2.确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
3.dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
4.确定遍历顺序
我们知道这是完全背包,
本题是求最小数!
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
5.举例推导dp数组
已输入n为5例,dp状态图如下:

Java代码实现
public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];for (int i = 0; i < dp.length; i++) {dp[i] = max;}dp[0] = 0;for (int i = 1; i * i <= n; i++) {for (int j = i * i; j <= n; j++) {if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}}return dp[n] == max ? -1 : dp[n];
}相关文章:

代码随想录算法训练营第四十五天 | 力扣 70. 爬楼梯(进阶), 322. 零钱兑换, 279.完全平方数
70. 爬楼梯(进阶) 题目 70. 爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 改为:一步一个台阶,两个台阶,三个台阶ÿ…...
dvwa靶场通关(三)
第三关:CSRF(跨站请求伪造) csrf跨站请求伪造:是一种对网站的恶意利用。尽管听起来像跨站脚本,但它与xss非常不同,xss利用站点内受信任用户,而csrf则通过伪造来自受信任用户的请求来利用受信任…...

【计算机图形学】理论考核回顾
写在前面: 1:题型主要是单选题多选题判断题计算题,题目量居多,一定要合理安排时间。 2:小题由于太琐碎了,遂不回顾,大致都是课件上做过的小题,嗯。 3:后续有时间更新期…...

一文了解国内外电子后视镜(CMS)现行法规标准
摘要: 本文小编分享一篇整合了国内外对CMS的安装及功能性做出要求的相关标准与法规。感兴趣的朋友可以专门去搜索学习。 前言:随着GB15084-2022的即将正式实施,以摄像头屏幕组合取代传统光学后视镜的新一代电子后视镜CMS相关车型将被允许上路…...
LabVIEWCompactRIO 开发指南36 确定“Clock Ticks”或模拟时间
LabVIEWCompactRIO 开发指南36 确定“Clock Ticks”或模拟时间 桌面执行节点可以控制模拟时间,因此开发人员可以使用模拟I/O在开发计算机上执行期间更改关键点的激励。要成功使用此功能,需要测量FPGA VI完成所需的时间,或者需要以直观地知道…...

ESP32 :项目的创建及项目架构解析
一、项目的创建 方式一:基于IDF示例创建 在ESP-IDF中有example示例库,以其中的一个示例为模板创建项目。 1、打开示例库 查看 - 命令面板(也可以按住CtrlShiftP 或 F1) 输入 show examples projects 2…...

TI EDI 项目数据库方案开源介绍
TI EDI 工作流简介 TI EDI到SQL Server示例流具有预配置的端口,用于从TI的EDI集成规范转换以下交易集: 850 采购订单,企业 -> TI855 采购订单确认,TI -> 企业860 采购订单变更,企业 -> TI865 采购订单变更确认,TI -> 企业856 发货通知,TI …...

报表控件FastReport使用指南——使用NuGet包创建PDF文档
FastReport 是功能齐全的报表控件,可以帮助开发者可以快速并高效地为.NET,VCL,COM,ActiveX应用程序添加报表支持,由于其独特的编程原则,现在已经成为了Delphi平台最优秀的报表控件,支持将编程开…...
策略模式-类型统计
文章目录 前言一、策略模式是什么?二、策略模式应用场景三、策略模式优点四、策略模式缺点五、场景案例:类型统计1.项目结构2.UML图解3.代码实现3.1 指标枚举3.2 请求体3.3 响应体3.4.分析统计指标策略3.5.接口3.6.扩展接口3.7.接口实现3.8.控制层 六、P…...

android 12.0app应用安装白名单
1.概述 在12.0定制化开发中,客户需求要实现应用安装白名单功能,在白名单之中的应用可以安装,其他的app不准安装,实现一个 控制app安装的功能,这需要从app安装流程入手就可以实现功能 PMS就是负责管理app安装的,功能就添加在这里就可以了, 2.app应用安装白名单核心代码 …...

android 12.0Launcher3禁止拖动图标到Hotseat
1.概述 在12.0系统Launcher3进行定制化开发中,对于hotseat的开发中,由功能需求要求禁止拖动图标到Hotseat的功能,而拖拽也是在workspace.java中处理的 接下来就从workspace.java 开始找解决的办法 2.Launcher3禁止拖动图标到Hotseat相关代码分析 packages/apps/Launcher3…...

Java阶段三Day03
Java阶段三Day03 文章目录 Java阶段三Day03JavaScript语言JavaScript概述什么是JavaScript语言特点一门编程语言包括哪些内容 语言基础变量JavaScript常用数据类型运算符各种语句如何在HTML页面中引入JavaScript代码方法和页面相关的方法 BOM和DOM什么是BOMwindow对象location对…...
【STM32G431RBTx】备战蓝桥杯嵌入式→决赛试题→第七届
文章目录 前言一、题目二、模块初始化三、代码实现interrupt.h:interrupt.h:main.h:main.h: 四、完成效果五、总结 前言 无 一、题目 二、模块初始化 1.LCD这里不用配置,直接使用提供的资源包就行 2.ADC:开启ADCsingle-ended 3.LED:开启PC8-15,PD2输出模式就行了…...
Java日期时间调整的几种方式
一、Calendar类 我们现在已经能够格式化并创建一个日期对象了,但是我们如何才能设置和获取日期数据的特定部分呢,比如说小时,日,或者分钟? 我们又如何在日期的这些部分加上或者减去值呢? 答案是使用Calendar 类。 Calendar类的…...
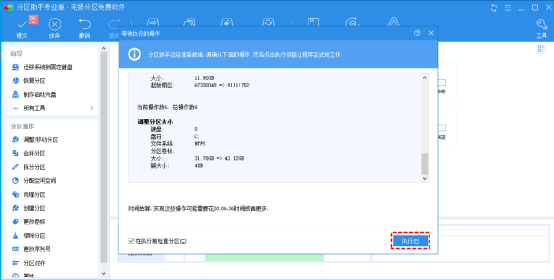
如何在Windows 11更新后解决C盘已满的问题?
Windows 11比Windows 10需要占用C盘更多的空间,在升级到Windows 11后,如果升级后出现问题,安装程序可以帮你退回到Windows 10。无论怎样,在升级到Windows 11后,系统会自动制作以前的数据的副本,这会占用大量…...
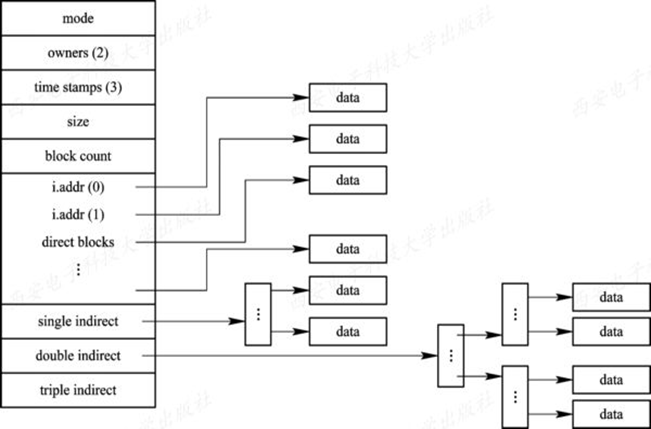
DJ6-1/2/3 文件系统
目录 6.1 文件系统概述 6.1.1 文件、记录和数据项 6.1.2 文件类型 6.1.3 文件系统模型 6.1.4 对文件的操作 6.2 文件的逻辑结构 6.2.1 文件逻辑结构的类型 6.2.2 顺序文件(Sequential File) 6.2.4 索引文件(Index File&…...

华为OD机试真题 Java 实现【打印文件】【2023Q1 100分】
一、题目描述 有 5 台打印机打印文件,每台打印机有自己的待打印队列。 因为打印的文件内容有轻重缓急之分,所以队列中的文件有1~10不同的优先级,其中数字越大优先级越高。 打印机会从自己的待打印队列中选择优先级最高的文件来打印。 如果存在两个优先级一样的文件,则选…...
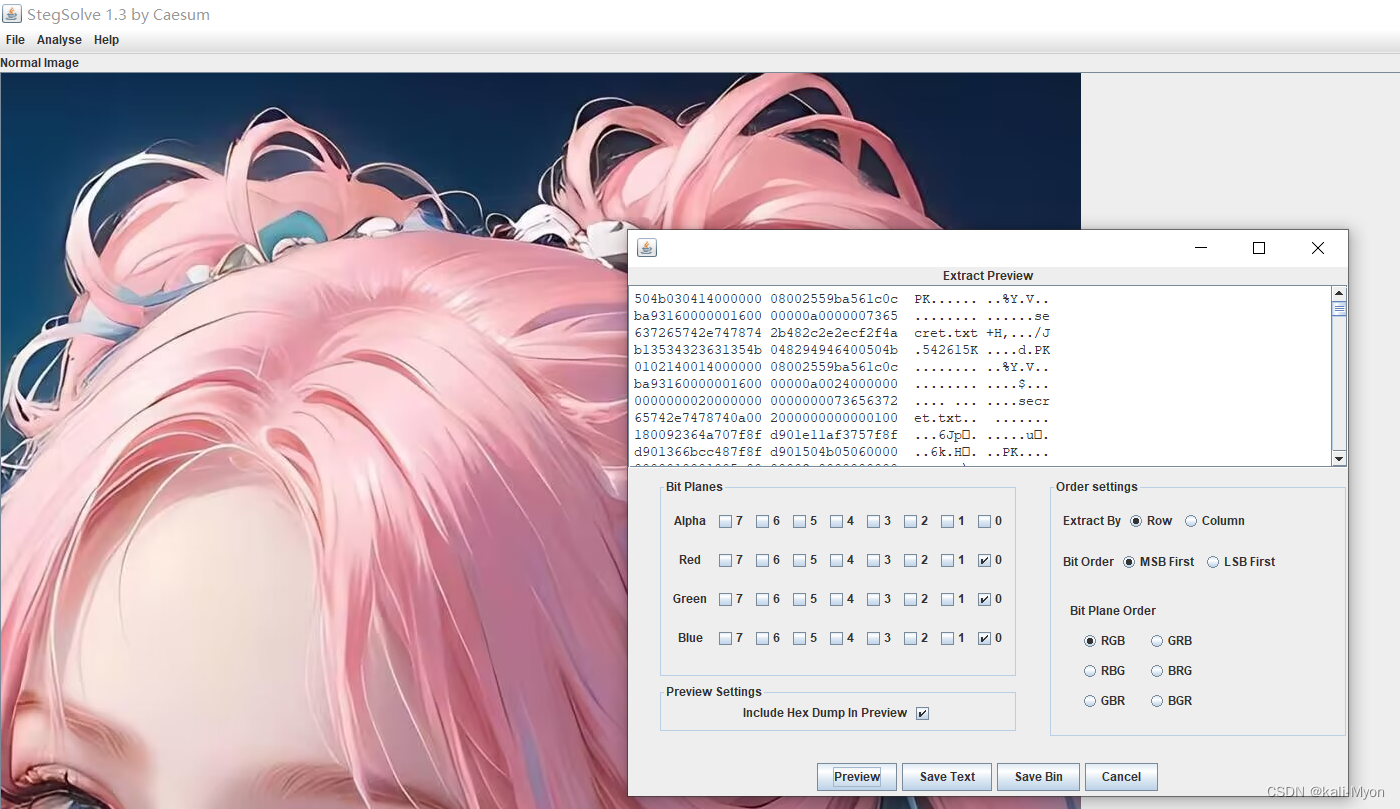
基于LSB实现文本、图片、压缩包的隐藏
关于LSB的相关介绍: LSB全称为 Least Significant Bit(最低有效位),是一种基于图片最低有效位修改储存信息的隐写方法,在CTF杂项中经常会遇到,LSB属于空域算法中的一种,是将信息嵌入到图像点中…...

(万字长文)Linux——IO之重定向+缓冲区 +重定向 +缓冲区原理实现 +带重定向的简易版shell+标准输出标准错误
索引 文件描述符分配规则重定向 缓冲区1.什么是缓冲区2.缓冲区在哪里 重定向源码模拟实现缓冲区原理带重定向的简易版Xshell标准输入和标准错误 文件描述符分配规则 文件描述符的分配规则 从头遍历数组fd_array[],找到一个最小的,没有被使用的下标,分配…...

面试:js 延迟加载方式
相关知识点: js 延迟加载,也就是等页面加载完成之后再加载 JavaScript 文件。 js 延迟加载有助于提高页面加载速度 一般有以下几种方式: defer 属性 async 属性 动态创建 DOM 方式 使用 setTimeout 延迟方法 让 JS 最后加载 js 的加载…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
