代码随想录算法训练营第四十二天 | 二维dp数组01背包, 力扣 416. 分割等和子集

背包

解析

1.确定dp数组以及下标的含义

对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

2.确定递推公式

有两个方向推出来dp[i][j]，

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3.dp数组如何初始化

dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。

一开始就统一把dp数组统一初始为0，更方便一些。

4.确定遍历顺序

先遍历 物品还是先遍历背包重量呢？

其实都可以！！ 但是先遍历物品更好理解。

5.举例推导dp数组

Java代码

public class BagProblem {public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagSize = 4;testWeightBagProblem(weight, value, bagSize);}private static void testWeightBagProblem(int[] weight, int[] value, int bagSize) {int goods = weight.length;int[][] dp = new int[weight.length][bagSize + 1];for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}for (int i = 1; i < weight.length; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}}for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}}

背包，一维dp数组（滚动数组）

解析

1.确定dp数组的定义

在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

2.一维dp数组的递推公式

dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]）

此时dp[j]有两个选择，一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，

所以递归公式为：

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3.一维dp数组如何初始化

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。

这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

4.一维dp数组遍历顺序

for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

 倒序遍历是为了保证物品i只被放入一次！

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

5.举例推导dp数组

一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下：

Java代码实现

public class BagProblem {public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagSize = 4;testWeightBagProblemScrollingArray(weight, value, bagSize);}private static void testWeightBagProblemScrollingArray(int[] weight, int[] value, int bagSize){int length = weight.length;int[] dp = new int[bagSize + 1];for (int i = 0; i < weight.length; i++) {for (int j = bagSize; j >= weight[i]; j--) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int j = 0; j <= bagSize; j++){System.out.print(dp[j] + " ");}}}

416. 分割等和子集

题目

416. 分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

解析

本题要求集合里能否出现总和为 sum / 2 的子集。

1.确定dp数组以及下标的含义

dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。

那么如果背包容量为target， dp[target]就是装满 背包之后的重量，所以 当 dp[target] == target 的时候，背包就装满了。

2.确定递推公式

本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

3.dp数组如何初始化

题目中 只包含正整数的非空数组，所以非0下标的元素初始化为0就可以了。

4.确定遍历顺序

使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

5.举例推导dp数组

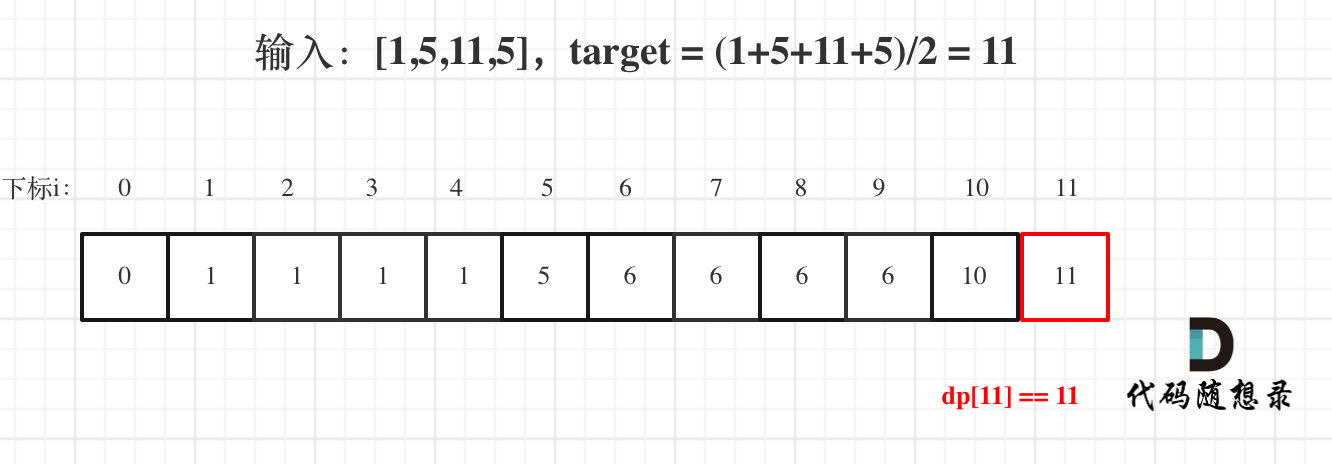
Java代码实现

public boolean canPartition(int[] nums) {if (nums == null || nums.length == 0) {return false;}int sum = 0;for (int num : nums) {sum += num;}if (sum % 2 != 0) {return false;}int target = sum / 2;int[] dp = new int[target + 1];for (int i = 0; i < nums.length; i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[target] == target;
}