算法基础学习笔记——⑫最小生成树\二分图\质数\约数
✨博主:命运之光
✨专栏:算法基础学习

目录
✨最小生成树
🍓朴素Prim
🍓Kruskal算法
✨二分图
🍓匈牙利算法
✨质数
🍓(1)质数的判定——试除法
🍓(2)分解质因数——试除法
✨约数
🍓(1)试除法求一个数的所有约数
🍓(2)约数个数
🍓(3)约数之和
🍓(4)欧几里得算法(辗转相除法)
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨最小生成树
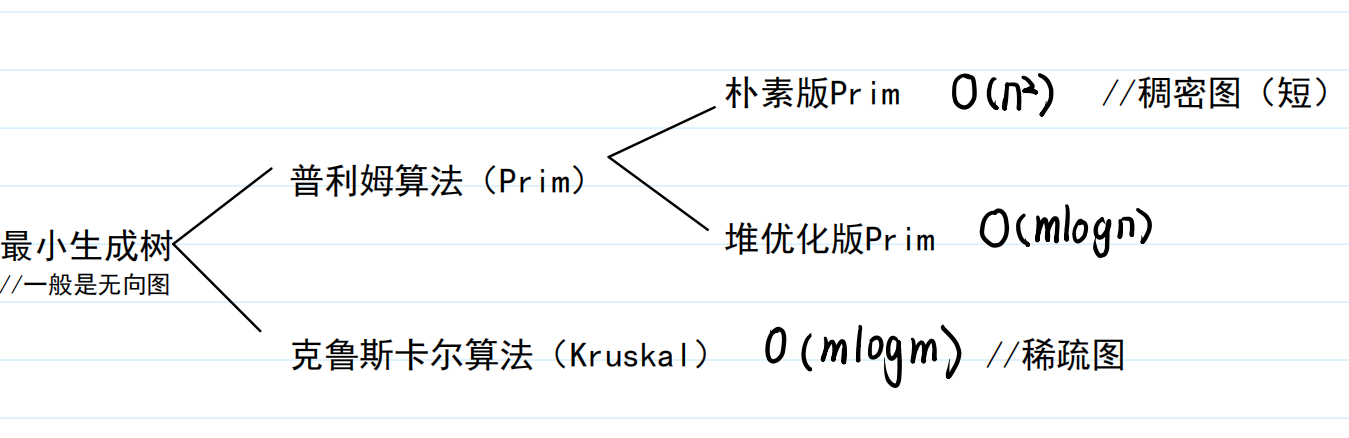
🍓朴素Prim
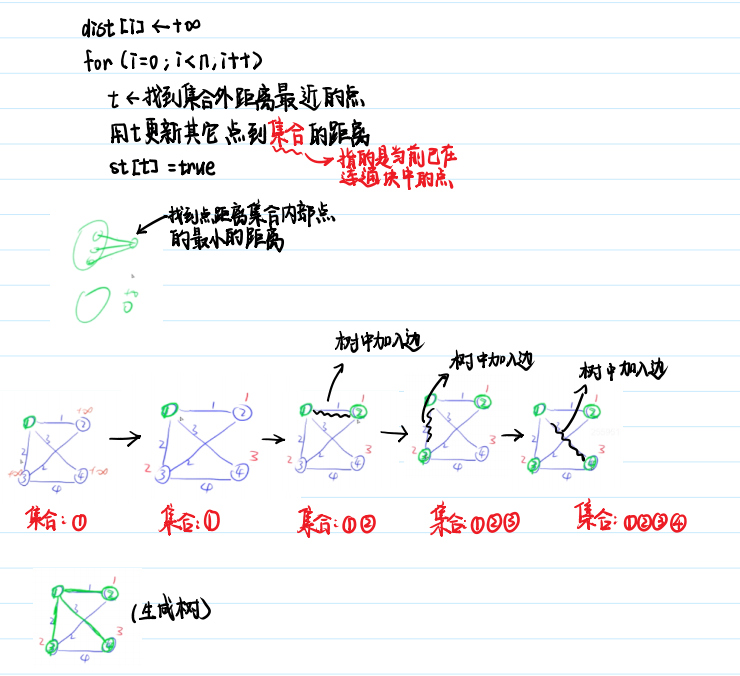
🍓朴素版prim算法:
时间复杂度是 O(n2+m)O(n2+m), nn 表示点数,mm 表示边数
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{memset(dist, 0x3f, sizeof dist);int res = 0;for (int i = 0; i < n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;if (i && dist[t] == INF) return INF;if (i) res += dist[t];st[t] = true;for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);}return res;
}🍓Kruskal算法

Kruskal算法:
时间复杂度是 O(mlogm)O(mlogm), nn 表示点数,mm 表示边数
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{int a, b, w;bool operator< (const Edge &W)const{return w < W.w;}
}edges[M];
int find(int x) // 并查集核心操作
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}
int kruskal()
{sort(edges, edges + m);for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集int res = 0, cnt = 0;for (int i = 0; i < m; i ++ ){int a = edges[i].a, b = edges[i].b, w = edges[i].w;a = find(a), b = find(b);if (a != b) // 如果两个连通块不连通,则将这两个连通块合并{p[a] = b;res += w;cnt ++ ;}}if (cnt < n - 1) return INF;return res;
}✨二分图

染色法
判断一个图是不是二分图
二分图:可以把所有点分成两边,使所有边在集合之间,集合内部没有边。
二分图当且仅当图中不含奇数环


🍓染色法判别二分图:
时间复杂度是 O(n+m)O(n+m), nn 表示点数,mm 表示边数
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{color[u] = c;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (color[j] == -1){if (!dfs(j, !c)) return false;}else if (color[j] == c) return false;}return true;
}
bool check()
{memset(color, -1, sizeof color);bool flag = true;for (int i = 1; i <= n; i ++ )if (color[i] == -1)if (!dfs(i, 0)){flag = false;break;}return flag;
}🍓匈牙利算法

🍓匈牙利算法:
时间复杂度是 O(nm)O(nm), nn 表示点数,mm 表示边数
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{memset(st, false, sizeof st);if (find(i)) res ++ ;
}✨质数
🍓所有大于1的自然数,所有<=1的数既不是质数也不是合数
定义:在大于1的整数中,如果只包含1和本身这两个约数,就被称为质数,或者叫素数
🍓(1)质数的判定——试除法
质数的一个重要性质:如果d能整除n,显然n除d也能整除n
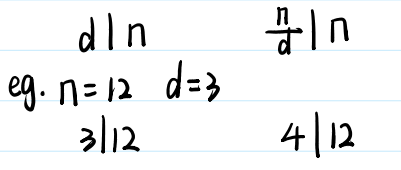
故发现n的所有的约数都是成对出现的(d与n/d都成成对出现的)
所以枚举时可以只枚举每一对当中较小的那一个,枚举:

🍓试除法判定质数:
bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i <= x / i; i ++ )if (x % i == 0)return false;return true;
}🍓(2)分解质因数——试除法

从小到大枚举所有数



🍓试除法分解质因数:
void divide(int x)
{for (int i = 2; i <= x / i; i ++ )if (x % i == 0){int s = 0;while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;}if (x > 1) cout << x << ' ' << 1 << endl;cout << endl;
}🍓筛

罗列出每个数,依次删除每个数的倍数,剩下的数就是质数,可以对此进行优化,可以不删每一个数的倍数, 可以只删质数的倍数,这样就不用重复删。
🍓质数定理:

优化完的筛法:埃氏筛法

🍓朴素筛法求素数:
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (st[i]) continue;primes[cnt ++ ] = i;for (int j = i + i; j <= n; j += i)st[j] = true;}
}
🍓线性筛法:
把每一个合数用它的某个质因子筛掉



每个数都会被其最小质因子筛掉,而且每个数只有一个最小质因子,故每个数只会被筛一次
🍓线性筛法求素数:
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}✨约数
约数
🍓(1)试除法求一个数的所有约数


🍓试除法求所有约数:
vector<int> get_divisors(int x)
{vector<int> res;for (int i = 1; i <= x / i; i ++ )if (x % i == 0){res.push_back(i);if (i != x / i) res.push_back(x / i);}sort(res.begin(), res.end());return res;
}🍓(2)约数个数
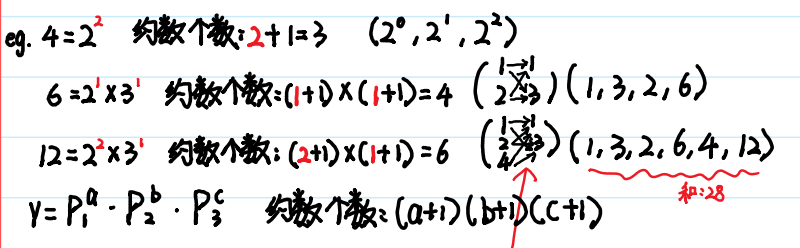
🍓(3)约数之和

约数个数和约数之和:
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
🍓(4)欧几里得算法(辗转相除法)

🍓欧几里得算法:
int gcd(int a, int b)
{return b ? gcd(b, a % b) : a; // <表达式1>?<表达式2>:<表达式3>,
} //它的意思是,如果表达式1成立,则输出表达式2的值,否则输出表达式3的值
补充小知识:
两个数的积等于它们最大公约数和它们最小公倍数的
积。公式表示为 :a×b=gcd(a,b)×lcm(a,b)
🍓最小公倍数与最大公约数模板:

相关文章:

算法基础学习笔记——⑫最小生成树\二分图\质数\约数
✨博主:命运之光 ✨专栏:算法基础学习 目录 ✨最小生成树 🍓朴素Prim 🍓Kruskal算法 ✨二分图 🍓匈牙利算法 ✨质数 🍓(1)质数的判定——试除法 🍓(2&…...

了解信号的传输方式、编码与调制、信道的极限容量
1.了解信号的传输方式、编码与调制、信道的极限容量 笔记来源: 湖科大教书匠:传输方式 声明:该学习笔记来自湖科大教书匠,笔记仅做学习参考 1.1 了解信号的传输方式 串行传输与并行传输 同步传输与异步传输 为什么需要收发双发…...

SpringBoot自动配置原理总结
1、我们需要从主启动类的SpringBootApplication注解开始分析: SpringBootApplication是一个复合注解,进入以后看到主要包括以下三个注解: SpringBootConfiguration EnableAutoConfiguration ComponentScan(excludeFilters { Filter(type …...

【LeetCode: 410. 分割数组的最大值 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

内核对象和两种同步
概念 Windows 中每个内核对象都只是一个内存块,它由操作系统内核分配,并只能由操作系统内核进 行访问 它的所有者:内核对象的所有者是操作系统内核,而非进程,也就是说当进程退出,内核对象不一定会销毁 法…...

水表远程监控系统有什么功能吗?
水表远程监控系统是通过远程传输水表数据,实现对水表的远程监控和管理的一种智能化系统。它主要具备以下功能: 1.远程抄表功能:通过远程传输技术,实现对水表的远程抄表和监控,无需人工上门抄表,节省人力成本…...
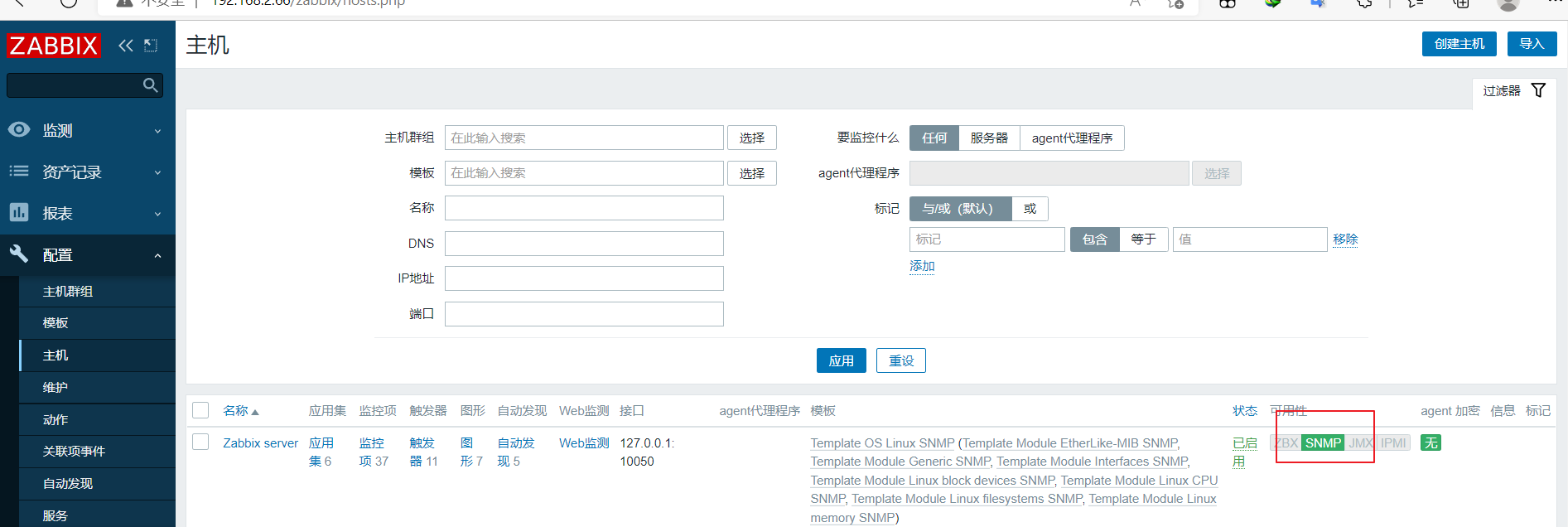
zabbix自定义监控
一、案例操作:自定义监控内容 案列:自定义监控客户端服务器登录的人数 需求:限制登录人数不超过 3 个,超过 3 个就发出报警信息 1、自定义监控内容的操作步骤 1.1 在客户端创建自定义 key 明确需要执行的 linux 命令 who | …...
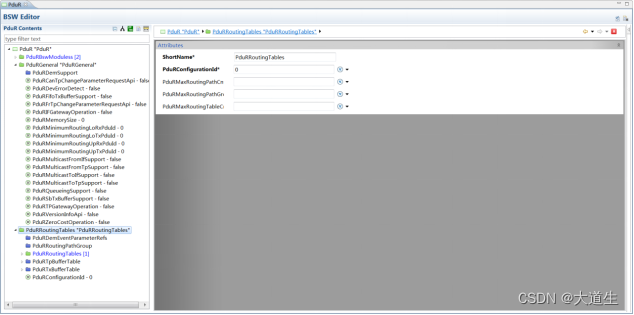
【AUTOSAR】Com通讯栈配置说明(四)---- Nm模块
Nm模块 NmGlobalConfig NmGlobalConstants NmRxIndicationCallback: callback 函数 NmCycletimeMainFunction:Nm 主函数调用周期 NmDevErrorDetect: 是否支持DET NmVersionInfoApi: 是否支持获取版本信息api PduR模块 PduRBswModules PduRBswModuleRef:关联的BS…...

IMG CXM GPU:面向复杂消费级设备的无缝视觉体验
上周我们推出了一款新的GPU,即IMG CXM。它的三种配置可扩展,为可穿戴设备和高级数字电视等多种消费设备提供无缝用户界面。 消费级设备需要GPU提供什么? 涵盖智能手表和智能眼镜的可穿戴市场为移动中的消费者提供了易于访问的信息。鉴于屏幕尺…...
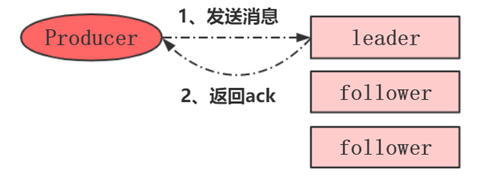
Kafka如何保证数据高可靠
Kafka它本身其实不是一个金融级别数据可靠的分布式消息系统。 虽然说它存储到某个topic里的数据会先拆分多个partition,这体现了分治的一个思想。每一个partition在最终存储的时候会保存多个副本,不同的副本存储在不同的节点。这样的话任意一个节点挂掉…...

OpenWRT 中修改SSID的文件
文件位置:/....../package/ramips/drivers/mt7628/files/mt7628.sh //---------------------------------------------文件中option ssid处修改如下: detect_mt7628() { # detect_ralink_wifi mt7628 mt7628 ssidmt7628-ifconfig eth0 | grep H…...
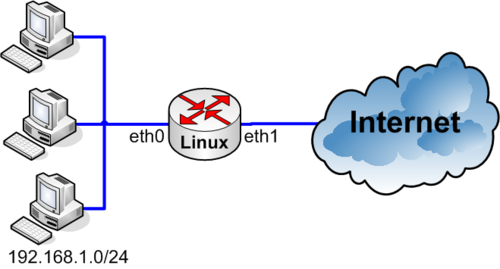
如何在 Linux 中进行网络地址转换 (NAT)?
网络地址转换(Network Address Translation,简称NAT)是一种在网络中使用的技术,它允许将私有网络中的IP地址映射到公共网络上,从而实现多个设备共享单个公共IP地址。在Linux系统中,我们可以使用一些工具和配…...

redis的使用第一章
下载地址:http://redis.io/download 安装步骤: 1.安装gcc yum install gcc2.把下载好的redis‐5.0.3.tar.gz放在/usr/local文件夹下,并解压 wget http://download.redis.io/releases/redis‐5.0.3.tar.gz tar xzf redis‐5.0.3.tar.gz cd r…...
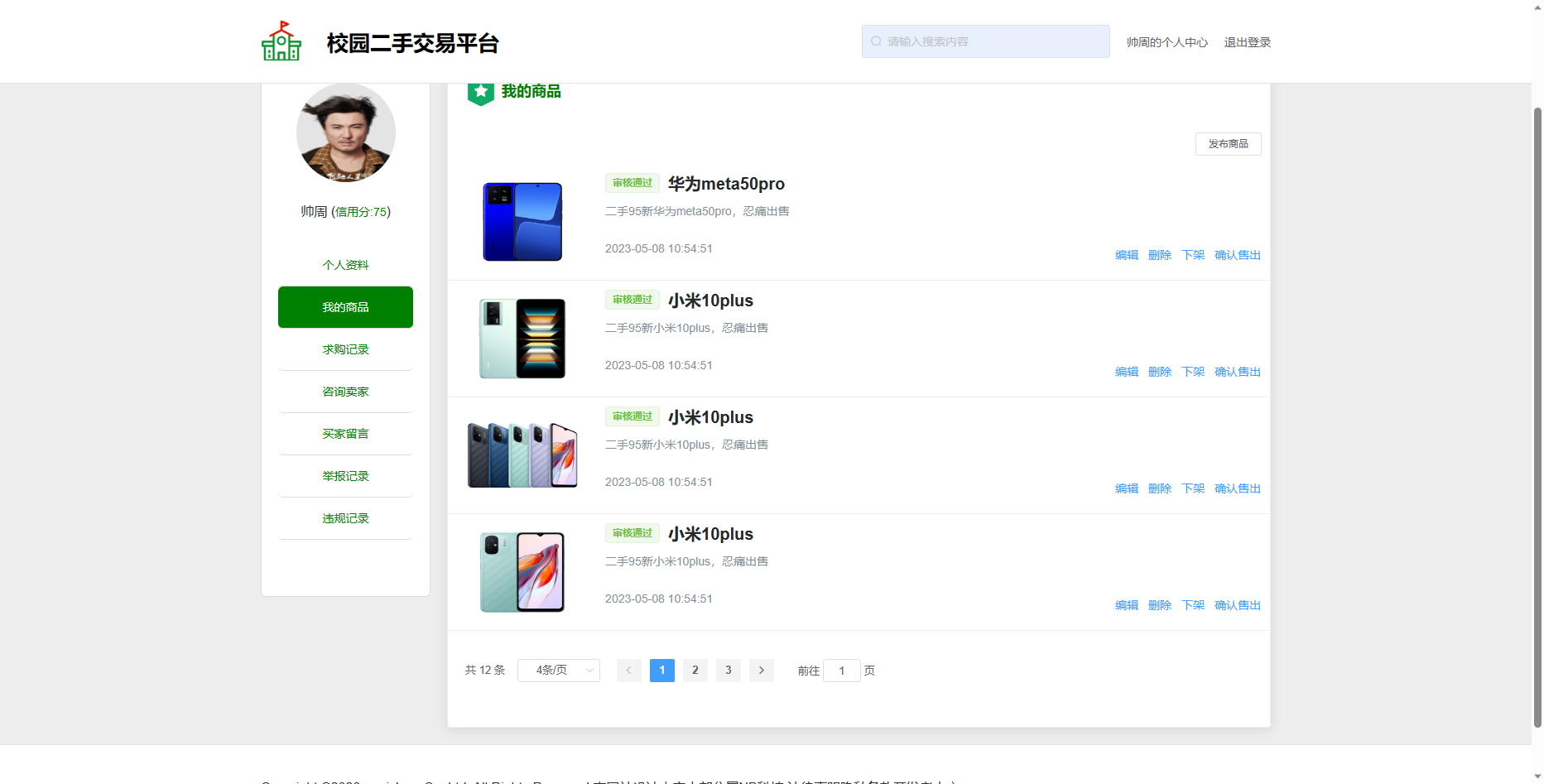
基于springboot+vue的校园二手交易市场
一、项目背景介绍: 校园二手交易市场是大学生生活中的重要组成部分,它为学生提供了一个便捷的方式来买卖物品。然而,传统的校园二手交易方式存在着信息不对称、交易风险高等问题。为了解决这些问题,基于Spring Boot和Vue的校园二手…...
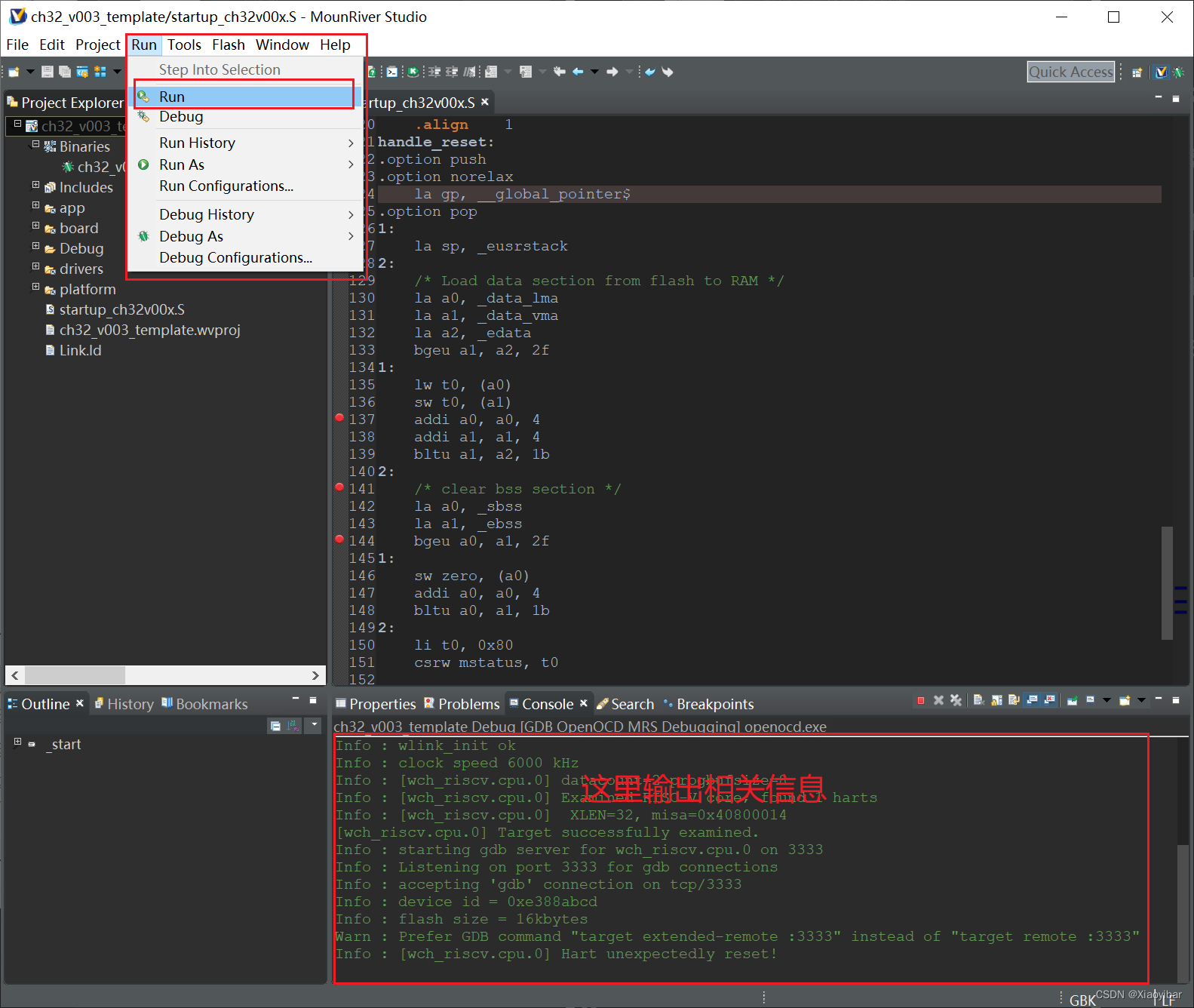
【CH32】| 01——新建工程 | 下载 | 运行 |调试
系列文章目录 【CH32】| 00——开发环境搭建 【CH32】| 01——新建工程 | 下载 | 运行 |调试 失败了也挺可爱,成功了就超帅。 文章目录 1. 新建工程1.1 基于官方IDE [MounRiver Studio]1.1.1 使用官方内置的工程模板新建1.1.2 使用自定义工程模板新建1.1.2.1 新建自…...
)
【Netty】Promise 源码分析(十七)
文章目录 前言一、Promise 接口二、Netty 的 DefaultPromise2.1、设置任务的成功或失败2.2、获取 Future 任务执行结果和添加监听事件 三、Netty 的 DefaultChannelPromise总结 前言 回顾Netty系列文章: Netty 概述(一)Netty 架构设计&…...
)
测牛学堂:2023最新自动化软件测试教程之python基础(字符串常用api总结)
python字符串常用API总结 1 count 查找某个字符在整个字符串中出现的次数 2 capitalize 将字符串的第一个字符转换为大写 3 center(width,fillchar) 返回一个指定宽度的字符串,fillchar为填充的字符,默认是空格,常用* str1 分隔线 print(st…...
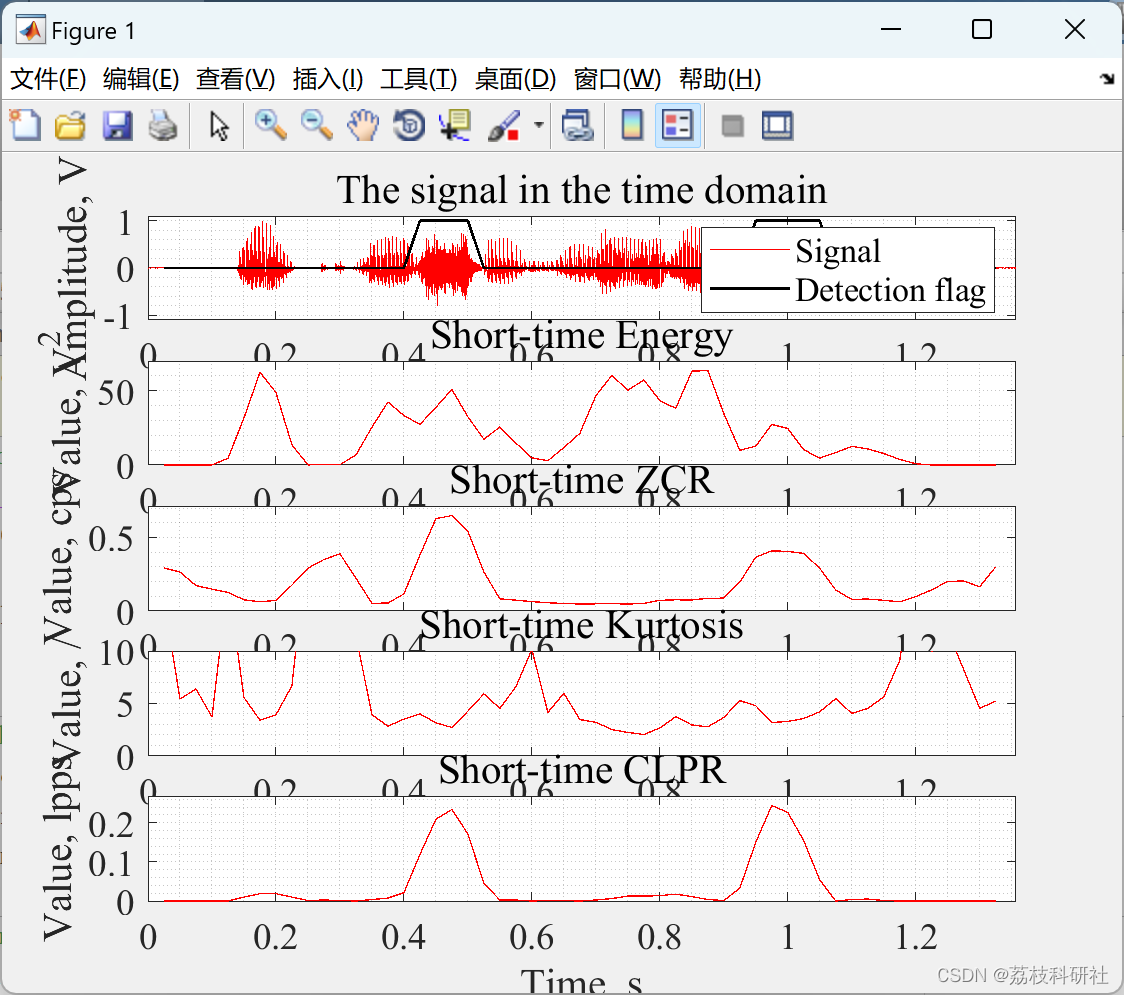
【信号变化检测】使用新颖的短时间条件局部峰值速率特征进行信号变化/事件/异常检测(Matlab代码实现)
、 💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭…...
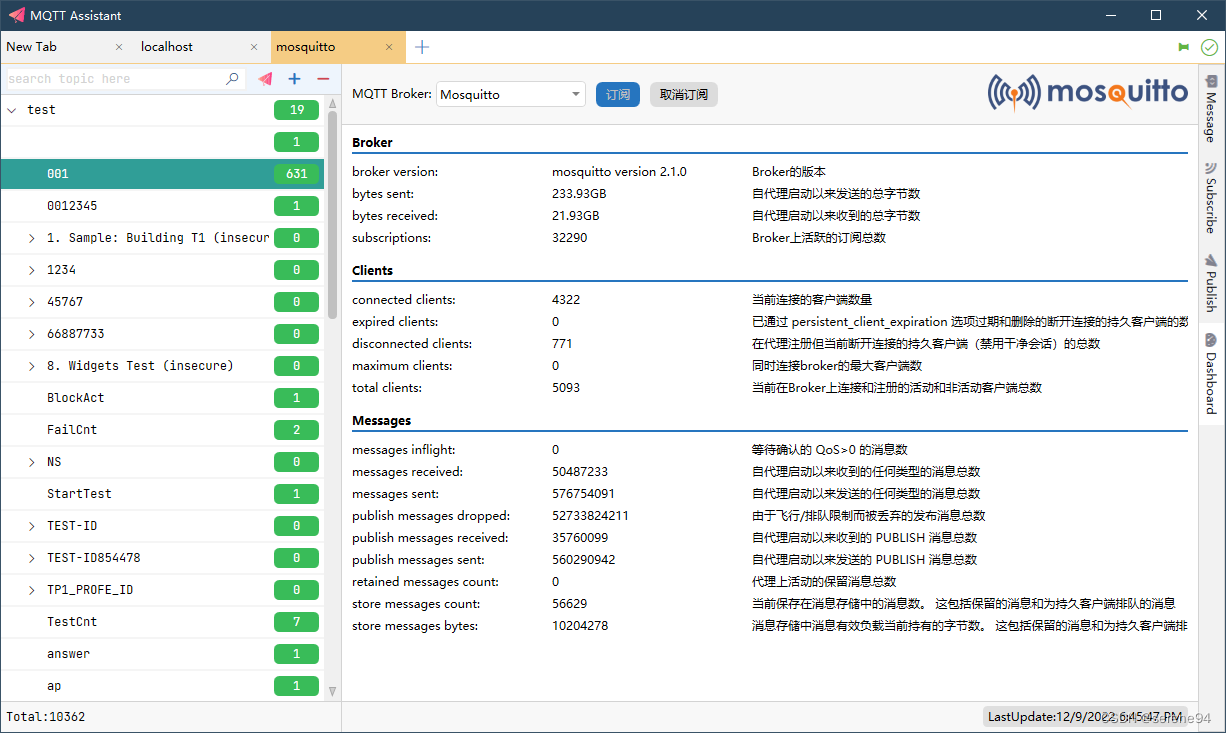
MQTT GUI 客户端 可视化管理工具
MQTT GUI 客户端 可视化管理工具 介绍 多标签页管理,同时打开多个连接提供原生性能,并且比使用 Electron 等 Web 技术开发的同等应用程序消耗的资源少得多支持 MQTT v5.0 以及 MQTT v3.1.1 协议,支持通过 WebSocket 连接至 MQTT 服务器以树…...

计算机硬件系统 — 冯诺依曼体系结构运行原理解析
目录 文章目录 目录计算机系统计算机硬件系统(冯诺依曼体系结构)PC 主机硬件CPU(中央处理器)CPU 的组成部分CPU 总线控制器单元运算器单元寄存器组超线程与多核架构三级高速缓存为什么需要缓存三级缓存结构 CPU 的指令集指令集的类…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
