【C++】二叉搜索树Binary Search Tree
Binary Search Tree
- 二叉搜索树的概念
- 二叉搜索树的操作
- 二叉搜索树的实现
- 查找
- 插入
- 删除
- 二叉搜索树的应用
- 二叉搜索树的性能分析
二叉搜索树的概念
二叉搜索树又被称为二叉排序树,顾名思义,当我们使用中序遍历时,会得到一个有序的序列。二叉搜索树有如下的性质:
1.若它的左子树不为空,则左子树上每个节点的值都小于根节点的值。
2.若它的右子树不为空,则右子树上每个节点的值都大于根节点的值。
3.左右子树也是二叉搜索树
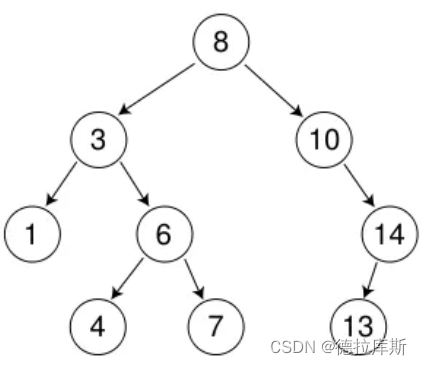
如图所示,就是一颗二叉搜索树。它的中序遍历结果为:1,3,4,6,7,8,10,13,14
二叉搜索树的操作
二叉搜索树的操作有:查找,插入,删除。
查找
1.从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找
2.最多查找高度次,走到到空,还没找到,这个值不存在
插入
分为树是否为空:
若为空树:树为空,则直接新增节点,赋值给root指针
若不为空树:按二叉搜索树性质查找插入位置,插入新节点
删除
首先要查找要删除的节点是否在二叉树中,若不存在,则直接返回,若存在,分情况进行删除。
a.要删除的节点没有孩子
b.要删除的节点只有左孩子
c.要删除的节点只有右孩子
d.要删除的节点左右孩子都有
实际上,对于删除操作来说,可以要删除没有孩子节点或删除只有一个孩子节点的情况,操作是相同的,都是直接将要删除的节点的双亲节点的指针指向当前删除节点的孩子节点。(当前节点如果没有孩子节点,实际上当前节点的孩子节点是nullptr,当前节点有孩子节点,实际上也是将双亲指向当前的孩子节点)
因此,可以将四种情况中a和b情况进行合并,那么就只有三种情况了。
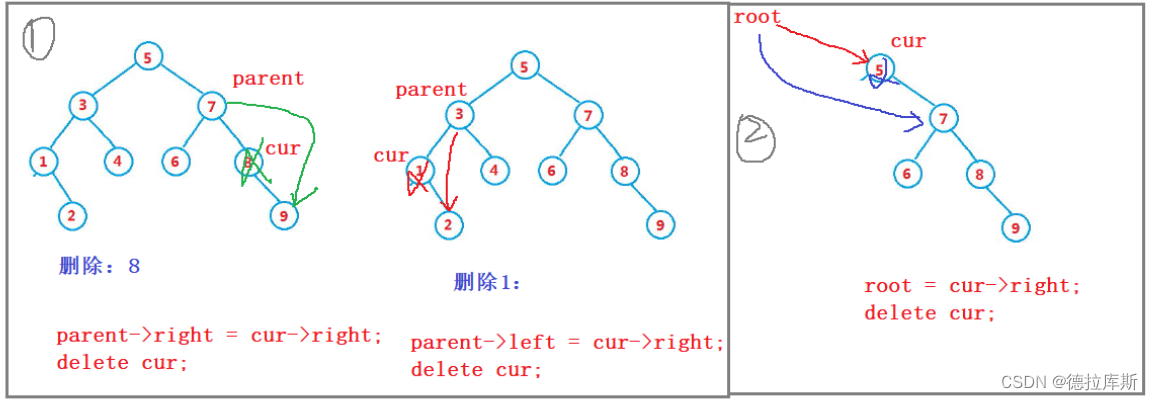
a.要删除的节点没有孩子或者只有右孩子-------将双亲节点指向当前节点的右孩子,然后直接删除当前节点
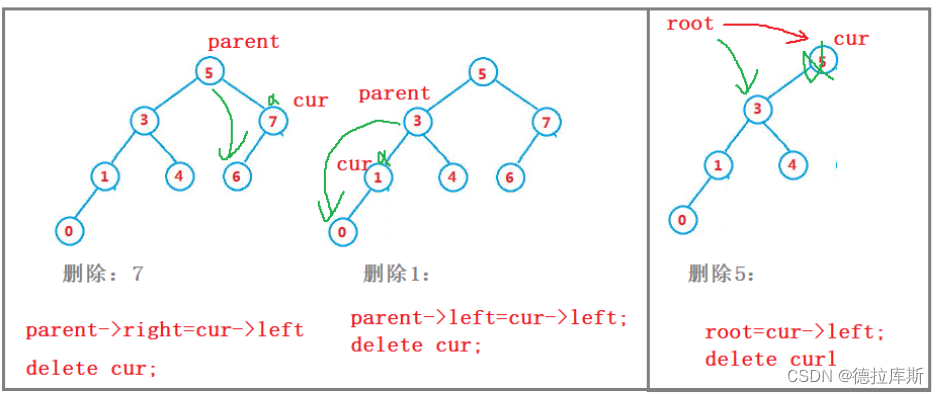
b.要删除的节点只有左孩子-------将双亲节点指向当前节点的左孩子,然后直接删除当前节点
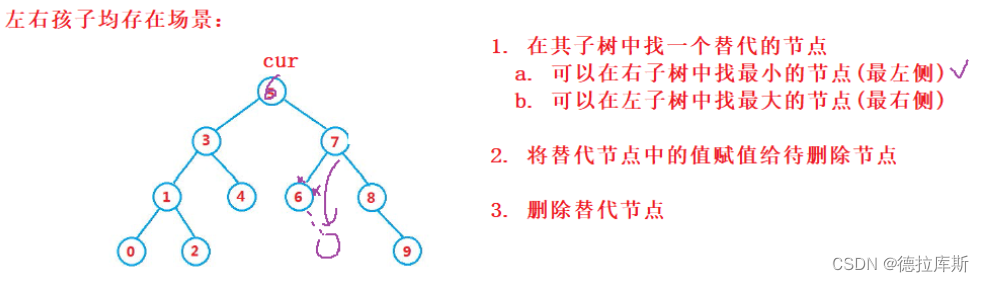
c.要删除的节点左右孩子都有------在它的右子树下找到最小的一个节点(右子树的最左侧),用它的值填补到被删除节点中,再处理该节点的删除问题
二叉搜索树的实现
查找
1.从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找
2.最多查找高度次,走到到空,还没找到,这个值不存在
Node* Find(const T& data){Node* cur = _root;while (cur){if (data > cur->_data){cur = cur->_right;}else if (data < cur->_data){cur = cur->_left;}elsereturn cur;}return nullptr;}
插入
分为树是否为空:
若为空树:树为空,则直接新增节点,赋值给root指针
若不为空树:按二叉搜索树性质查找插入位置,插入新节点
bool Insert(const T& data){//空树,插入成功后就是根节点if (_root == nullptr){_root = new Node(data);return true;}//非空就需要找到待插入的位置。Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_data > data)cur = cur->_left;else if (cur->_data < data)cur = cur->_right;elsereturn false;} cur = new Node(data);if (cur->_data > parent->_data){parent->_right = cur;}elseparent->_left = cur;return true;}
删除
首先要查找要删除的节点是否在二叉树中,若不存在,则直接返回,若存在,分情况进行删除。
a.要删除的节点没有孩子
b.要删除的节点只有左孩子
c.要删除的节点只有右孩子
d.要删除的节点左右孩子都有
实际上,对于删除操作来说,可以要删除没有孩子节点或删除只有一个孩子节点的情况,操作是相同的,都是直接将要删除的节点的双亲节点的指针指向当前删除节点的孩子节点。(当前节点如果没有孩子节点,实际上当前节点的孩子节点是nullptr,当前节点有孩子节点,实际上也是将双亲指向当前的孩子节点)
因此,可以将四种情况中a和b情况进行合并,那么就只有三种情况了。
a.要删除的节点没有孩子或者只有右孩子-------将双亲节点指向当前节点的右孩子,然后直接删除当前节点
b.要删除的节点只有左孩子-------将双亲节点指向当前节点的左孩子,然后直接删除当前节点
c.要删除的节点左右孩子都有------在它的右子树下找到最小的一个节点(右子树的最左侧),用它的值填补到被删除节点中,再处理该节点的删除问题
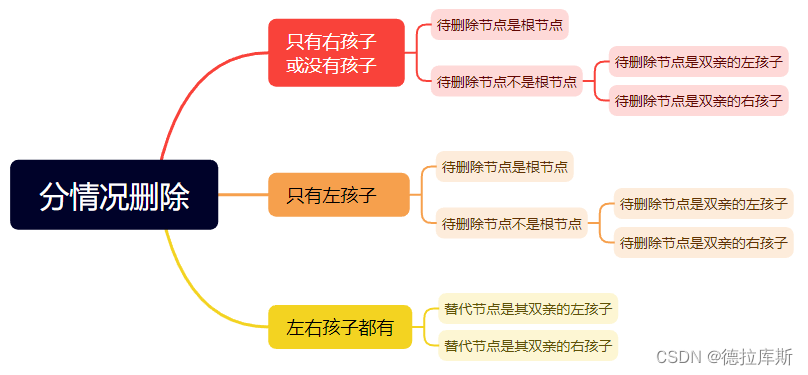
最终我们可以将情况分为上述的a b c三种情况,
对于情况a来说,其内部又可以分为两大类:要删除的是根节点要删除的不是根节点
对于情况b来说,其内部又可以分为两大类:要删除的是根节点要删除的不是根节点
对于情况c来说,我们是通过步骤:1.在待删除节点的右子树中找到最小的节点(替代节点) 2.将替代节点的值赋给待删除的节点 3.删除找到的替代节点.
而在a情况中,针对要删除的节点不是根节点,我们需要判断待删除的节点是其双亲节点的左孩子还是右孩子。因为到时候需要让双亲节点指向待删除节点的左孩子
而在b情况中,针对要删除的节点不是根节点,我们需要判断待删除的节点是其双亲节点的左孩子还是右孩子。因为到时候需要让双亲节点指向待删除节点的右孩子
而在c情况中,我们需要判断替代节点的是其双亲的左孩子还是右孩子。因为到时候需要让双亲节点指向待删除节点的右孩子
下图是上述分类情况的图示。
只有右孩子的场景
只有左孩子的场景
左右孩子均存在的场景
这个是对于删除操作需要分的情况:
针对上述分的情况,代码的实现
bool Erase(const T& data){//找待删除节点的位置,并且保存双亲Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur ;if (data == cur->_data)break;else if (data < cur->_data){parent = cur;cur = cur->_left;}else{parent = cur;cur = cur->_right;}}//值在BST中不存在值为data的节点if (cur == nullptr)return false;// 只有右孩子或者没有孩子if (cur->_left == nullptr){// 1.双亲为空,说明为根节点if (parent == nullptr)_root = cur->_right;// 2.双亲非空,说明不是根节点else{//可能是双亲的左孩子if (cur = parent->_left)parent->_left = cur->_right;//也可能是双亲的右孩子elseparent->_right = cur->_right;}delete cur;}//只有左孩子else if (cur->_right == nullptr){// 1.双亲为空,是根节点if (parent == nullptr)_root = cur->_left;// 2.双亲不为空,不是根节点else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}//左右孩子均存在,//先在其右子树中找到最左边的节点,//将替代节点中的值赋给要删除的节点,//删除替代节点else{Node* tmp = cur->_right;parent = cur;//在cur的右子树中找替代节点while (tmp->_left){parent = tmp;tmp = tmp->_left;}//用替代节点中的值替换待删除的节点cur->_data = tmp->_data;//删除替代节点if (parent->_left == tmp)parent->_left = tmp->_right;elseparent->_right = tmp->_right;delete tmp;}return true;
二叉搜索树的应用
k模型和kv模型
k模型是指:只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
例如:要查找一个单词是否拼写正确,我们可以先将所有的单词作为key构建一个二叉搜索树。在这个二叉搜索树中去查找是否有我们想找到的单词,若可以找到,则证明拼写正确,若找不到,则证明拼写错误。
kv模型是指:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
例如:英汉词典是一个典型的kv模型,通过英文可以快速找到与其对应的中文。英文和中文就构成了一对键值对
二叉搜索树的性能分析
因为对应二叉搜索树来说,插入和删除操作都要先进行查找,查找的效率高低直接决定了各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
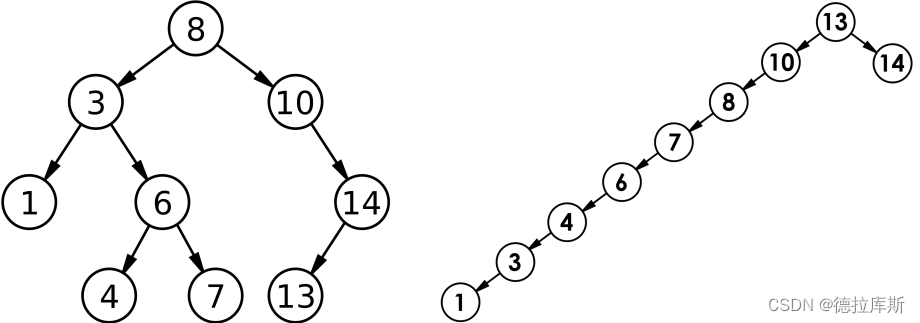
如果关键码集合,插入的次序接近于无序,则会构造出作图这样的二叉搜索树,而插入的次序如果是有序的,则会构造出右图这样的单支树。
而不同的二叉搜索树,其比较的平均次数是不同的。
最优情况下:二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:O(logN)(以2为底)
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:O(N)(以2为底)
正是由于插入的次序不同,会导致构造的二叉搜索树的结构不同,而退化成单枝时,二叉搜索树就失去了优势,因此如果需要按照任意次序插入时,都能让二叉搜索树的性能达到最优,就需要用到AVL树和红黑树了。
相关文章:

【C++】二叉搜索树Binary Search Tree
Binary Search Tree 二叉搜索树的概念二叉搜索树的操作二叉搜索树的实现查找插入删除 二叉搜索树的应用二叉搜索树的性能分析 二叉搜索树的概念 二叉搜索树又被称为二叉排序树,顾名思义,当我们使用中序遍历时,会得到一个有序的序列。二叉搜索…...

Hover.css动画库的使用
目录 1、 Hover.css是什么? 2、引入 2.1、整个文件引入 2.2、复制所需要的代码 案例: 1. 卷边效果 2. 调整大小的卷边 类别: 1、 Hover.css是什么? Hover.css是一个CSS3鼠标悬停的动画方案,里面包含了许多纯c…...
)
Baumer工业相机堡盟工业相机如何通过文件保存和导入的方式保存和载入相机的各类参数(C#)
Baumer工业相机堡盟工业相机如何通过文件保存和导入的方式使保存和载入相机的各类参数(C#) Baumer工业相机Baumer工业相机BGAPISDK中UserSet的技术背景相机配置文件代码案例分享第一步:保存相机当前参数设置doUserSetStore为文件第二步&#…...

封装设计!抽象BasePage,提升WEB自动化测试用例质量和效率
目录 前言: 一、什么是抽象BasePage 二、BasePage中的属性和方法 三、BasePage中的代码实现 四、抽象Page对象 五、测试用例 六、总结 前言: 对于测试工程师来说,WEB自动化测试是非常重要的一部分。然而,WEB自动化测试的开…...
)
c primer plus学习笔记(一)
1.int的大小恒定就是32位么? 不是的,int大小是跟着系统走的,不是在各个系统里固定不变的。 32位系统int就是32位。64位系统,int就是64位。short 和long的长度则跟着int走,一般来说int是32位,short就是16位…...
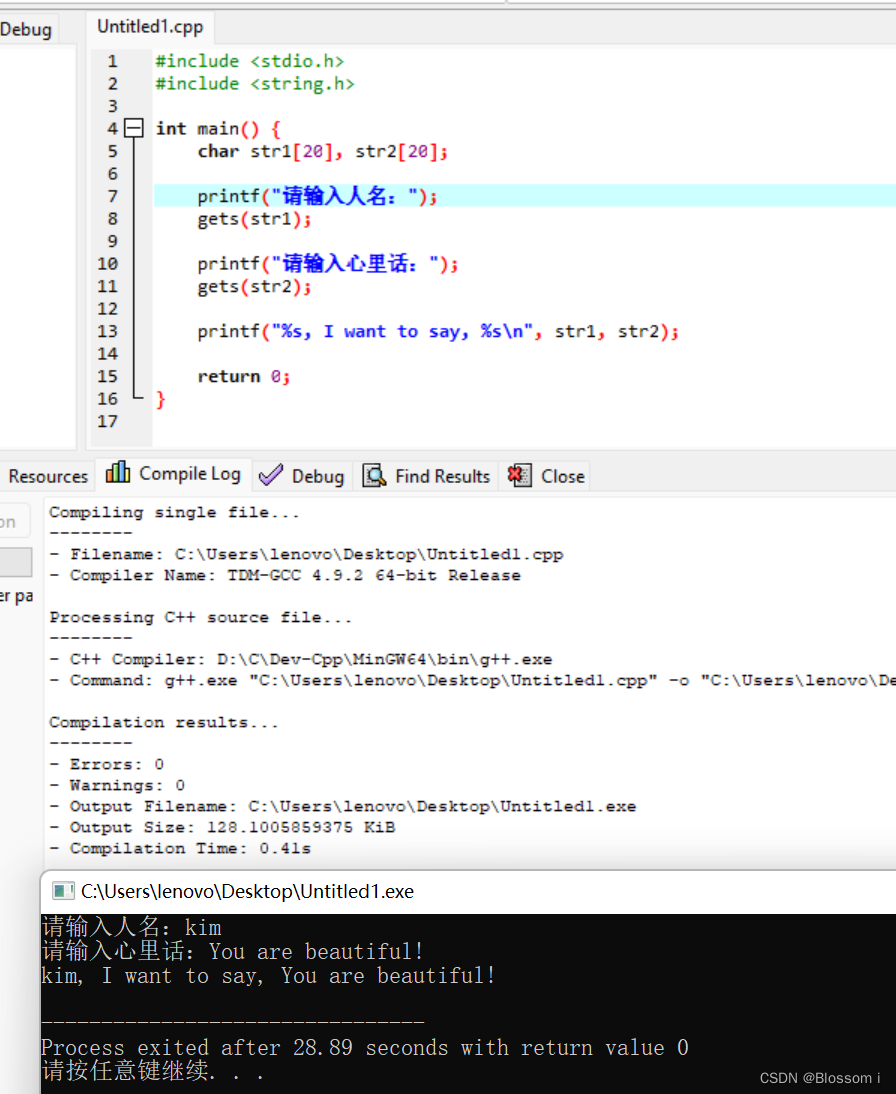
C语言2:说心里话
描述 分两次从控制台接收用户的两个输入:第一个内容为“人名”,第一个内容为“心里 话”。 然后将这两个输入内容组成如下句型并输出出来: 1.(人名),I want to say,(心里话 2. 输入输出示例: 输入ÿ…...

任务19 简单个人电话号码查询系统
系列文章 任务19 简单个人电话号码查询系统 问题描述 人们在日常生活中经常需要查找某个人或某个单位的电话号码,本实验将实现一个简单的个人电话号码查询系统,根据用户输入的信息(例如姓名等)进行快速查询。基本要求 (1) 在外存…...

day4--链表内指定区间反转
迭代方法 1. 第m个节点的前一个节点pre和第n个节点; 2. 将第m个节点到第n个节点的链表部分反转; 3. 将pre节点的next指向反转后链表的头节点,将反转后链表的尾节点的next指向n1节点。 /*** struct ListNode {* int val;* struct ListNode…...

HTTP状态码是什么?常用的状态码有什么?
HTTP(Hypertext Transfer Protocol)是一种用于传输超文本和其他内容的应用层协议。 历史: HTTP最早的版本是HTTP/0.9,它只支持简单的 GET 请求,而不支持其他操作。 HTTP/1.0 版本增加了许多新特性,如支持…...
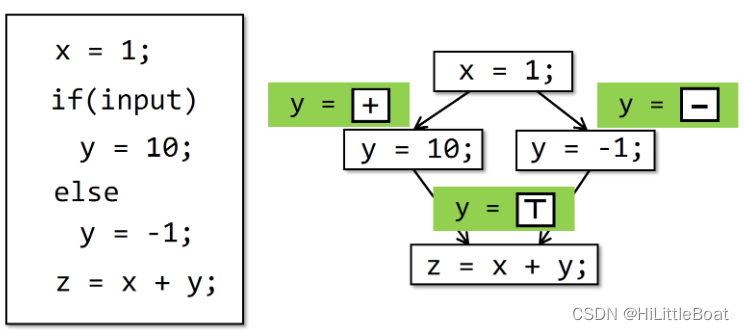
【软件分析/静态分析】学习笔记01——Introduction
🔗 课程链接:李樾老师和谭天老师的:南京大学《软件分析》课程01(Introduction)_哔哩哔哩_bilibili 目录 一、静态程序分析介绍 1.1 PL and Static Analysis 程序语言和静态分析 1.2 为什么要学 Static Analysis? …...
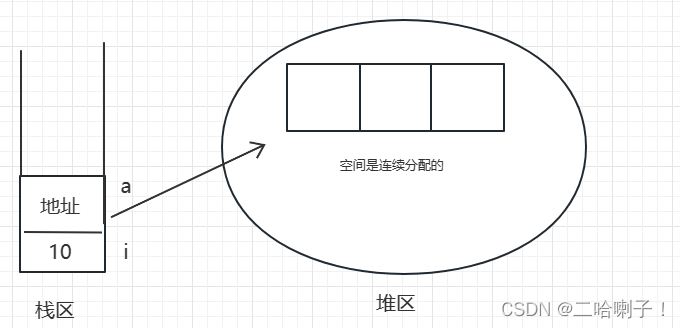
Java数组
文章目录 前言一维数组数组定义创建数组数组的内存模型数组数据初始化数组元素访问遍历数组length常见数组异常 二分查找数组的操作数组的复制数组的排序 二维数组扩展 Java中定义数组的语法如下: 数据类型[] 数组名 new 数据类型[数组长度]; 数据类型指的是数组中…...

【数据库原理入门】
数据库原理:深入探索与实践指南 引言 在我们的日常生活中,数据库无处不在,从在线购物、银行交易到社交媒体,都离不开数据库。要想成为一名出色的开发者,理解数据库原理是非常重要的。本文将以简明易懂的方式…...
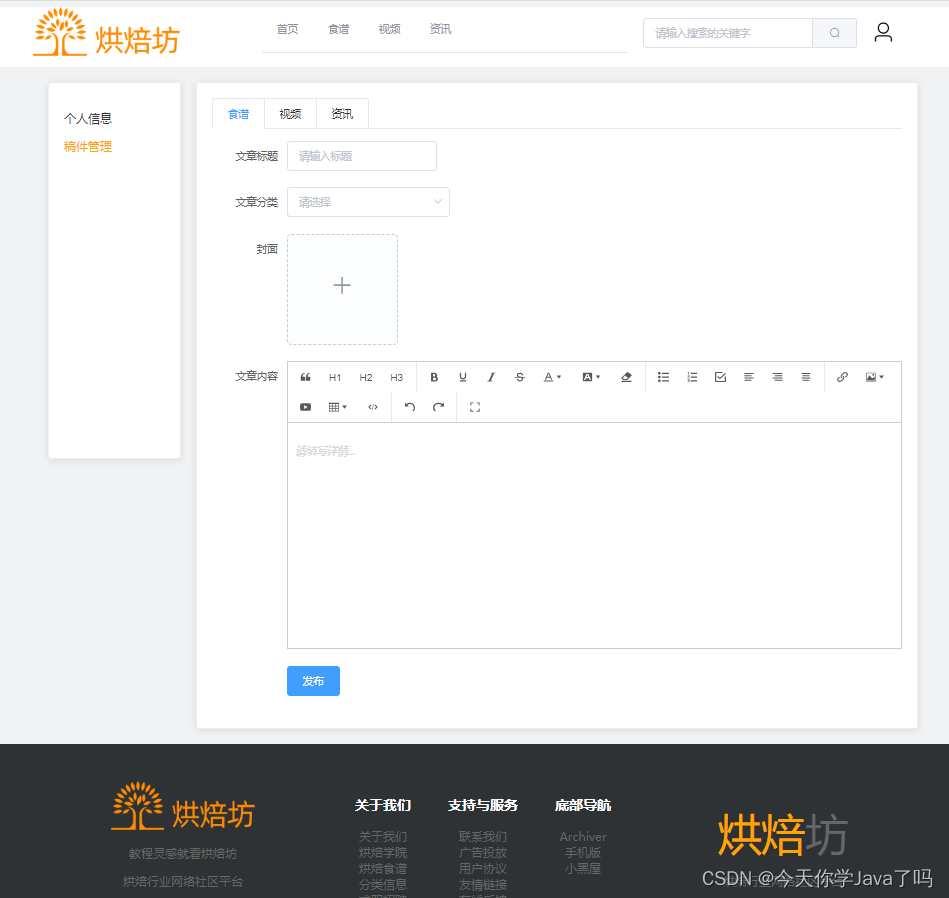
练习Vue烘培坊项目
烘培坊项目 文章目录 烘培坊项目项目概述项目页面展示后台管理页面登录页面文章详情页面稿件发布页面 项目关键代码实现后台管理页面稿件管理页面内容列表页面文章详情页面烘培坊主页面注册页面登录页面个人信息页面稿件发布页面 项目概述 烘培坊(Bakery࿰…...
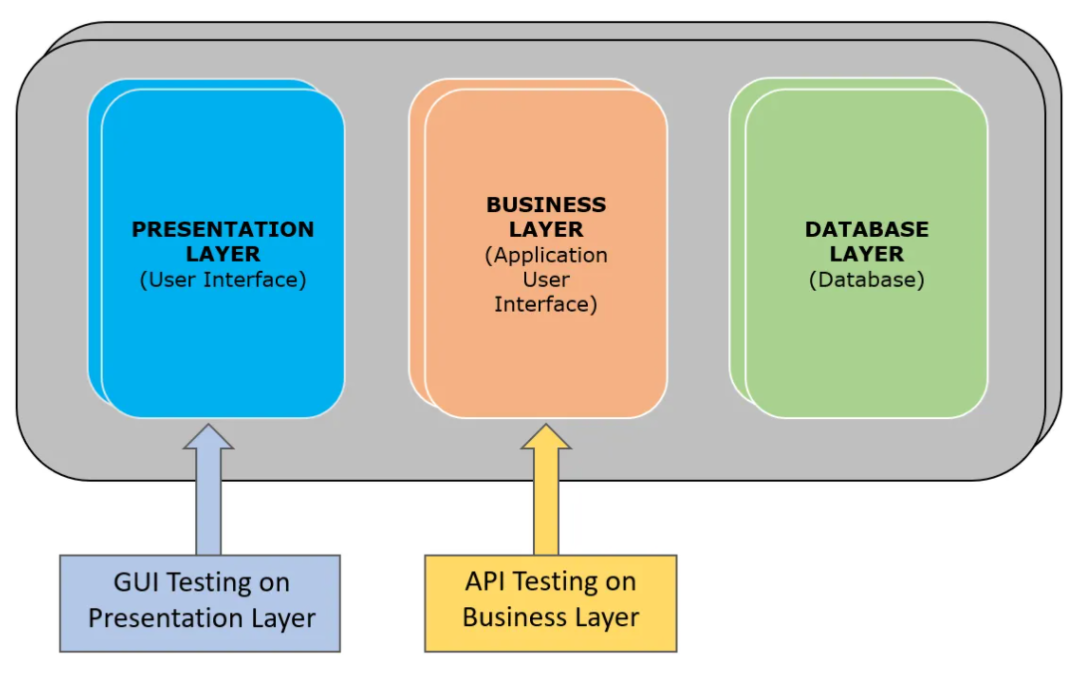
API测试| 了解API接口测试| API接口测试指南
什么是API? API是一个缩写,它代表了一个 pplication P AGC软件覆盖整个房间。API是用于构建软件应用程序的一组例程,协议和工具。API指定一个软件程序应如何与其他软件程序进行交互。 例行程序:执行特定任务的程序。例程也称为过…...

使用canvas给图片添加水印
上接文章“图片处理” canvas元素其实就是一个画布,我们可以很方便地绘制一些文字、线条、图形等,它也可以将一个img标签里渲染的图片画在画布上。 我们在上传文件到后端的时候,使用input标签读取用户本地文件后得到的其实是一个Blob对象&a…...
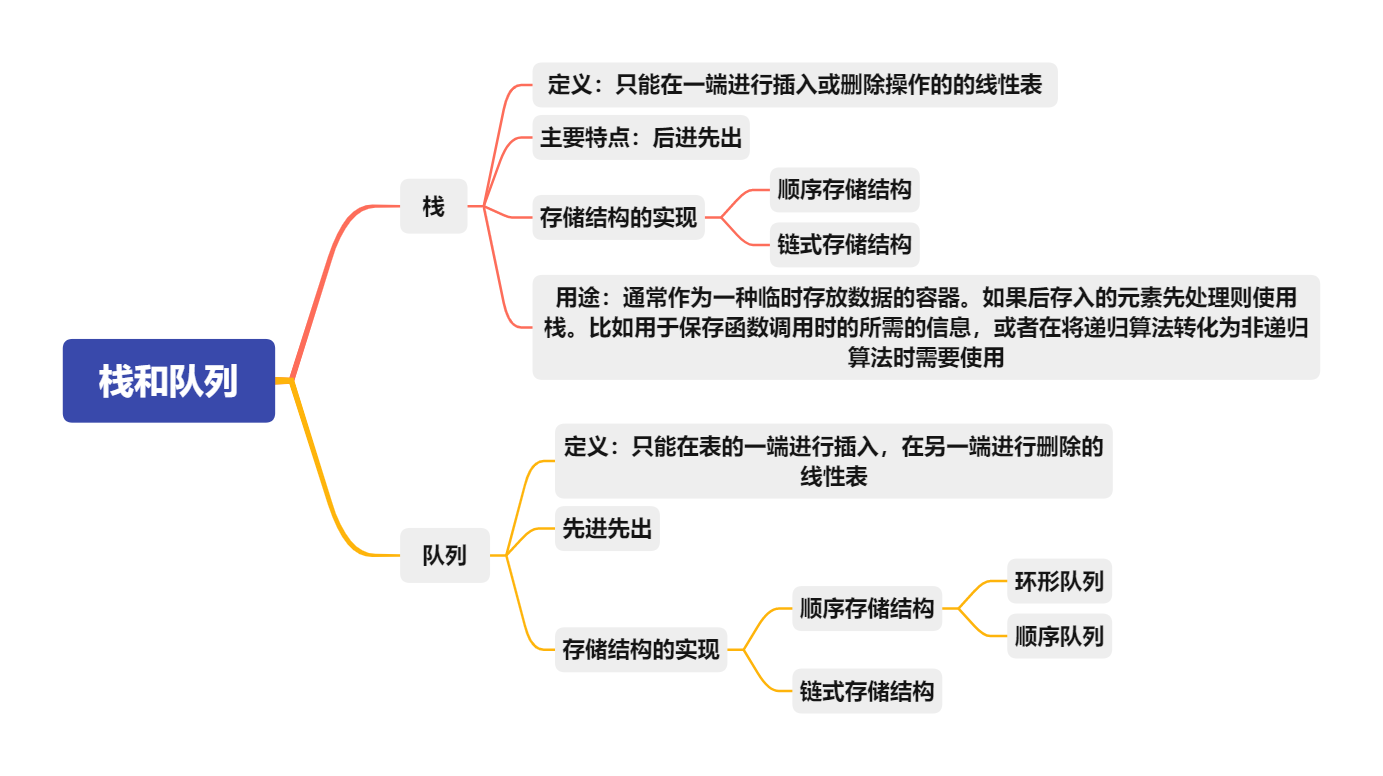
栈和队列的概念和实现
栈 栈 定义:只能在一端进行插入或删除操作的的线性表 主要特点:后进先出 存储结构的实现 顺序存储结构 链式存储结构 用途:通常作为一种临时存放数据的容器。如果后存入的元素先处理则使用栈。比如用于保存函…...
PostgreSQL 源码部署
文章目录 说明1. 准备工作1.1 源码包下载1.2 解压安装目录1.3 安装依赖包1.4 添加用户1.5 创建数据目录 2. 编译安装2.1 源码编译2.2 配置环境变量2.3 初始化数据库2.4 启动数据库2.5 连接数据库 3. 参数调整3.1 配置 pg_hba3.2 监听相关2.4 日志文件2.5 内存参数 说明 本篇文…...

医疗IT系统安科瑞隔离电源装置在医院的应用
【摘要】介绍该三级综合医院采用安科瑞隔离电源系统5件套,使用落地式配电柜安装方式,从而实现将TN系统转化为IT系统,以及系统绝缘情况监测。 【关键词】医用隔离电源系统;IT系统;绝缘情况监测;三级综合医院…...

高压放大器在3D打印中的应用
随着3D打印技术的快速发展,高压放大器在3D打印中的应用越来越受到人们的关注。高压放大器在3D打印中扮演着非常重要的角色,可以提高3D打印的效率和精度,从而实现更高的打印质量。本文将详细介绍高压放大器在3D打印中的应用及其原理。 高压放…...

chatgpt赋能python:Python中的三角函数介绍
Python中的三角函数介绍 Python作为一种高级编程语言,可以处理基础算术运算、三角函数等高等数学的操作。其中,三角函数是常用的数学函数之一,Pyhon中的三角函数包括正弦函数、余弦函数、正切函数等。 正弦函数 正弦函数在三角学中是最基本…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...