算法Day15 | 层序遍历,102,107,199,637,429,515,116,117,104,111,226,101
Day15
- 层序遍历
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历 II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
- 226.翻转二叉树
- 101.对称二叉树
层序遍历
层序遍历就相当于图论中的广度优先搜索。
递归遍历就相当于图论中的深度优先搜索。
只使用二叉树结构,无法层序遍历。因为当你遍历到一个某个节点左节点时,无法遍历到其右节点。需要一个其他结构来辅助。选择使用队列queue保存每一层待遍历的元素。
102.二叉树的层序遍历
题目链接:102.二叉树的层序遍历
迭代
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;//记录每层节点vector<vector<int>> res;if (root) que.push(root);while (!que.empty()) {vector<int> res1;int size = que.size();//用于记录弹出节点个数,就是每层节点个数while (size--) {TreeNode* cur = que.front();que.pop();res1.push_back(cur->val);//记录节点数值if (cur->left) que.push(cur->left);//左节点入队列if (cur->right) que.push(cur->right);//右节点入队列}res.push_back(res1);}return res;}
};
递归
class Solution {
public:void recursive(TreeNode* cur, vector<vector<int>>& res, int depth) {if (!cur) return;//返回条件if (res.size() == depth) res.push_back(vector<int>());//开辟一个空的vector<int>
// if (res.size() == depth) res.emplace_back();等价于上一行res[depth].push_back(cur->val);recursive(cur->left, res, depth + 1);//depth+1是回溯recursive(cur->right, res, depth + 1);//depth+1是回溯}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;int depth = 0;//给res二维数组,用来赋外层索引recursive(root, res, depth);return res;}
};
107.二叉树的层次遍历 II
题目链接:107.二叉树的层次遍历 II
因为节点遍历只能从根节点开始。所以就正常层序遍历,最后结果反转一下。
迭代
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> res;queue<TreeNode*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();vector<int> res1;while (size--) {TreeNode* cur = que.front();que.pop();res1.push_back(cur->val);if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}res.push_back(res1);}reverse(res.begin(), res.end());return res;}
};
递归
class Solution {
public:void recursion(TreeNode* root, vector<vector<int>>& res, int depth) {if (!root) return;if (res.size() == depth) res.emplace_back();res[depth].emplace_back(root->val);recursion(root->left, res, depth + 1);//depth+1是回溯recursion(root->right, res, depth + 1);//depth+1是回溯}vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> res;int depth = 0;recursion(root, res, depth);reverse(res.begin(), res.end());return res;}
};
199.二叉树的右视图
题目链接:199.二叉树的右视图
迭代
class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*> que;vector<int> res;if (root) que.push(root);while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();if (!size)/*size = 0*/ res.push_back(cur->val);if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return res;}
};
递归
class Solution {
public:void recursion(TreeNode* root, vector<int>& res, int depth) {if (!root) return;if (res.size() == depth) res.emplace_back(root->val);//先加入右节点元素,因为是保存右节点recursion(root->right, res, depth + 1);//depth+1是回溯recursion(root->left, res, depth + 1);//depth+1是回溯}vector<int> rightSideView(TreeNode* root) {vector<int> res;int depth = 0;recursion(root, res, depth);return res;}
};
637.二叉树的层平均值
题目链接:637.二叉树的层平均值
class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {vector<double> res;queue<TreeNode*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();double sum = 0;int cnt = 0;while (size--) {TreeNode* cur = que.front();que.pop();sum += cur->val;++cnt;if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}res.push_back(sum / cnt);}return res;}
};
429.N叉树的层序遍历
题目链接:429.N叉树的层序遍历
class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> que;vector<vector<int>> res;if (root) que.push(root);while (!que.empty()) {int size = que.size();vector<int> res1;while (size--) {Node* cur = que.front();que.pop();res1.push_back(cur->val);for (auto& i : cur->children) {que.push(i);}}res.push_back(res1);}return res;}
};
515.在每个树行中找最大值
题目链接:515.在每个树行中找最大值
class Solution {
public:vector<int> largestValues(TreeNode* root) {vector<int> res;queue<TreeNode*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();int maxValue = INT_MIN;while (size--) {TreeNode* cur = que.front();que.pop();maxValue = max(maxValue, cur->val);if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}res.push_back(maxValue);}return res;}
};
116.填充每个节点的下一个右侧节点指针
题目链接:116.填充每个节点的下一个右侧节点指针
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();while (size--) {Node* cur = que.front();que.pop();if (size) cur->next = que.front();//如果不是最后一个,与下一个节点相连if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return root;}
};
117.填充每个节点的下一个右侧节点指针II
题目链接:117.填充每个节点的下一个右侧节点指针II
与上一道题一模一样
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();while (size--) {Node* cur = que.front();que.pop();if (size) cur->next = que.front();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return root;}
};
104.二叉树的最大深度
题目链接:104.二叉树的最大深度
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;if (root) que.push(root);int res = 0;while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}++res;}return res;}
};
111.二叉树的最小深度
题目链接:111.二叉树的最小深度
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> que;if (!root) return 0;if (root) que.push(root);int res = 1;//至少有一层while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);if (!cur->left && !cur->right) return res;}++res;}return res;}
};
226.翻转二叉树
题目链接:226.翻转二叉树
前、后序遍历很简单。
前序递归
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;swap(root->left, root->right);//中invertTree(root->left);//左invertTree(root->right);//右return root;}
};
后序递归
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;invertTree(root->left);//左invertTree(root->right);//右swap(root->left, root->right);//中return root;}
};
中序递归:代码上看是两次root->left
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;invertTree(root->left);//左swap(root->left, root->right);//中//因为上一行代码已经处理过左树,处理完换成右树//接下来要处理的是原来的右树,但是已经变成左树了invertTree(root->left);//右return root;}
};
前序迭代
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root) st.push(root);while (!st.empty()) {TreeNode* cur = st.top();if (cur) {st.pop();if (cur->right) st.push(cur->right);//右if (cur->left) st.push(cur->left);//左st.push(cur);//中st.push(nullptr);} else {st.pop();cur = st.top();st.pop();swap(cur->left, cur->right);}}return root;}
};
中序迭代
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root) st.push(root);while (!st.empty()) {TreeNode* cur = st.top();st.pop();if (cur) {if (cur->right) st.push(cur->right);//右st.push(cur);//中st.push(nullptr);if (cur->left) st.push(cur->left);//左} else {cur = st.top();st.pop();swap(cur->left, cur->right);}}return root;}
};
后序迭代
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root) st.push(root);while (!st.empty()) {TreeNode* cur = st.top();st.pop();if (cur) {st.push(cur);st.push(nullptr);if (cur->right) st.push(cur->right);if (cur->left) st.push(cur->left);} else {cur = st.top();st.pop();swap(cur->left, cur->right);}}return root;}
};
层序迭代
class Solution {
public:TreeNode* invertTree(TreeNode* root) {queue<TreeNode*> que;if (root) que.push(root);while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();swap(cur->left, cur->right);if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return root;}
};
101.对称二叉树
题目链接:101.对称二叉树
因为是先判断左右是否对称,再将结果传给中。顺序为左右中。所以是后序遍历。
递归
class Solution {
public:bool recursion(TreeNode* cur1, TreeNode* cur2) {//先排除空节点//这两个语句不能调换if (!cur1 && !cur2) return true;//非空之后,再排除值。if (!cur1 || !cur2 || cur1->val != cur2->val/*值判断一定要在非空之后*/) return false;auto outside = recursion(cur1->left, cur2->right);auto inside = recursion(cur1->right, cur2->left);return outside && inside;}bool isSymmetric(TreeNode* root) {if (!root) return true;return recursion(root->left, root->right);}
};
对于判断条件需要强调:
if (!cur1 && !cur2) return true;
if (!cur1 || !cur2) return false;
第一个if判断了同时为空的条件,满足条件,执行return。如果执行到第二条if语句,表示第一个if一定失效,即cur1和cur2不可能同时为空(有cur1为空,则cur2不为空;cur1不为空,则cur2为空),所以第二个if只需要判断cur1不为空(cur2一定为空)或者cur2不为空(cur1一定为空)即可。重要的是这两条if不能颠倒顺序。
if (!cur1 && !cur2) return true;
if (!cur1 && cur2) return false;
if (cur1 && !cur2) return false;
也就是,上面三条if可以用两条if来代替。因为第二条的if中的cur2和第三条if中的cur1一定是非空的,是多余的。
由于if后是return语句,所以可以不写else,先if( && )再写if( || )。更具一般性地,if( && ) else if ( || )。
迭代
class Solution {
public:bool isSymmetric(TreeNode* root) {if (!root) return true;stack<TreeNode*> st;st.push(root->left);st.push(root->right);while (!st.empty()) {auto leftNode = st.top();st.pop();auto rightNode = st.top();st.pop();if (!leftNode && !rightNode) continue;if (!leftNode || !rightNode || leftNode->val != rightNode->val)return false;st.push(leftNode->left);st.push(rightNode->right);st.push(leftNode->right);st.push(rightNode->left);}return true;}
};
相关文章:

算法Day15 | 层序遍历,102,107,199,637,429,515,116,117,104,111,226,101
Day15 层序遍历102.二叉树的层序遍历107.二叉树的层次遍历 II199.二叉树的右视图637.二叉树的层平均值429.N叉树的层序遍历515.在每个树行中找最大值116.填充每个节点的下一个右侧节点指针117.填充每个节点的下一个右侧节点指针II104.二叉树的最大深度111.二叉树的最小深度 226…...
Prometheus+Grafana学习(十一)安装使用pushgateway
Pushgateway允许短暂和批量作业将其指标暴露给 Prometheus。由于这些工作的生命周期可能不足够长,不能够存在足够的时间以让 Prometheus 抓取它们的指标。Pushgateway 允许它们可以将其指标推送到 Pushgateway,然后 Pushgateway 再将这些指标暴露给 Prom…...

深入理解C/C++预处理器指令#pragma once以及与ifndef的比较
#pragma once用法总结 为了防止重复引用造成二义性 在C/C中,在使用预编译指令#include的时候,为了防止重复引用造成二义性,通常有两种方式 第一种是#ifndef指令防止代码块重复引用,比如说 #ifndef _CODE_BLOCK #define _CODE_BLO…...
git 环境配置 + gitee拉取代码
好嘛 配环境的时候 老是忘记这个命令行 干脆自己写一个记录一下 也不用搜了 1.先从git官网下载git 安装 2.然后从gitee拉取代码的时候提示 这是因为换了新电脑没有加入新的公钥啦 哎 所以老是记不住命令行 first : git config --global user.name “Your Name” …...

港联证券|港股拥抱特专科技企业 内资券商“修炼内功”蓄势而为
港股市场新一轮改革举措渐次落地。特别是港交所推出特专科技公司上市机制,吸引符合资格的科技企业申请赴港上市,成为这一轮港股市场改革的“重头戏”。 作为香港资本市场的重要参与者,内资券商立足香港、背靠内地、辐射全球,走出一…...

多项创新技术加持,实现零COGS的Microsoft Editor语法检查器
编者按:Microsoft Editor 是一款人工智能写作辅助工具,其中的语法检查器(grammar checker)功能不仅可以帮助不同水平、领域的用户在写作过程中检查语法错误,还可以对错误进行解释并给出正确的修改建议。神经语法检查器…...
Python编程环境搭建:Windows中如何安装Python
在 Windows 上安装 Python 和安装普通软件一样简单,下载安装包以后猛击“下一步”即可。 Python 安装包下载地址:https://www.python.org/downloads/ 打开该链接,可以看到有两个版本的 Python,分别是 Python 3.x 和 Python 2.x&…...

Sui Builder House首尔站倒计时!
Sui主网上线后的第一场Builder House活动即将在韩国首尔举行,同期将举办首场线下面对面的黑客松。活动历时两天,将为与会者提供独特的学习、交流和娱乐的机会。活动详情请查看:Sui Builder House首尔站|主网上线后首次亮相。 Sui…...

Java设计模式-状态模式
简介 在软件开发领域,设计模式是一组经过验证的、被广泛接受的解决问题的方案。其中之一是状态模式,它提供了一种优雅的方式来管理对象的不同状态。 状态模式是一种行为型设计模式,它允许对象在内部状态发生改变时改变其行为。状态模式将对…...

智慧社区用什么技术开发
智慧社区是指利用信息技术和先进的管理理念,将社区内的各种公共服务进行整合和优化,提高社区居民的生活品质和社区管理的效率。为了实现智慧社区的建设,需要采用多种技术,包括但不限于以下几种: 1.物联网技术…...

多线程 线程池饱和策略
RejectedExecutionHandler(饱和策略):当队列和线程池都满了,说明线程池处于饱和状态,那么必须采取一种策略处理提交的新任务。 这个策略默认情况下是AbortPolicy,表示无法处理新任务时抛出异常。 在JDK 1…...

进程间通信之信号
进程间通信之信号 1. 信号2. 信号由谁产生?3. 有哪些信号4. 信号的安装5. 信号的发送1) 使用kill函数2)使用alarm函数3) 使用raise6.发送多个信号7. 信号集1. 信号 什么是信号? 信号是给程序提供一种可以处理异步事件的方法,它利用软件中断来实现。不能自定义信号,所有信号…...

二分查找三道题
二分查找 两种写法:左闭右闭[left,right]、左闭右开[left,right) 主要有几点不同:1. right是从num.length开始还是从num.length-1开始。2.left<还是<right。3.rightmid还是mid1 左闭右闭写法: public int search(int[] nums, int targ…...
MyBatis 框架
MyBatis 框架 MyBatis 简介搭建 MyBatis 开发环境核心配置文件详解mapper 映射文件(实现增删改查)MyBatis获取参数值的两种方式MyBatis的各种查询功能特殊SQL的执行自定义映射resultMapresultMap 字段和属性的映射多对一映射处理一对多映射处理 动态SQLM…...
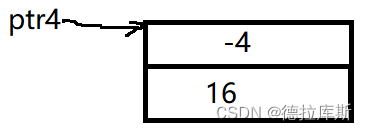
【C++】虚表和虚基表到底有哪些区别?
虚表和虚基表 虚表虚基表虚拟继承和虚函数都存在时的对象模型 虚表 我们知道,如果类中声明了的方法是用virtual进行修饰的,则说明当前这个方法要作为虚函数,而虚函数的存储和普通函数的存储是有区别的 当有虚函数声明时,编译器会…...
剑指 Offer 04. 二维数组中的查找解题思路
文章目录 标题解题思路优化 标题 在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整…...

冯诺依曼体系结构详解
一.冯诺伊曼体系结构的概念: 约翰冯诺依曼(John von Neumann,1903.1.28-1957.2.8),美籍匈牙利数学家,计算机科学家,物理学家。是20世纪最重要的数学家之一,后来被称为计算机之父。 后…...

ISO证书“带标”与“不带标”的区别是什么?
ISO9001质量管理体系认证是企业产品获得“通行绿卡”的最直接最有效的途径。 通过认证在打破贸易壁垒,提高产品知名度,降低生产成本,提高经济效益,维护消费者权益,减少重复审核负担等方面的作用越来越为企业界所共知。…...
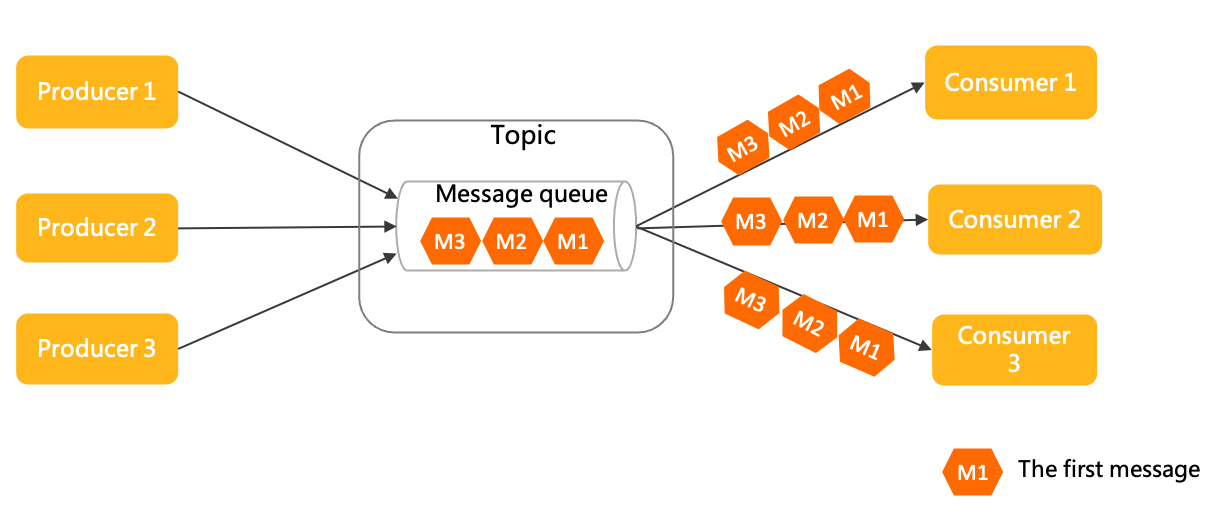
RocketMQ 领域模型概述
本文为您介绍 Apache RocketMQ 的领域模型。 Apache RocketMQ 是一款典型的分布式架构下的中间件产品,使用异步通信方式和发布订阅的消息传输模型。通信方式和传输模型的具体说明,请参见下文通信方式介绍和消息传输模型介绍。 Apache RocketMQ 产品具备…...

黄河千年清一回与人类健康
黄河千年清一回奏响一曲曲让人类走进幸福新时代的壮丽凯歌。疫情之后的首届全世界健康产业发展大会 5 月28 日上午 9 时在中国首都北京召开 The Yellow River has played a magnificent song of triumph in the millennium, ushering humanity into a new era of happiness. T…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
