第三章 向量与线性方程组
引言
- 题型总结中推荐例题有蓝皮书的题型较为重要,只有吉米多维奇的题型次之。
- 码字不易,如果这篇文章对您有帮助的话,希望您能点赞、评论、收藏,投币、转发、关注。您的鼓励就是我前进的动力!
知识点思维导图
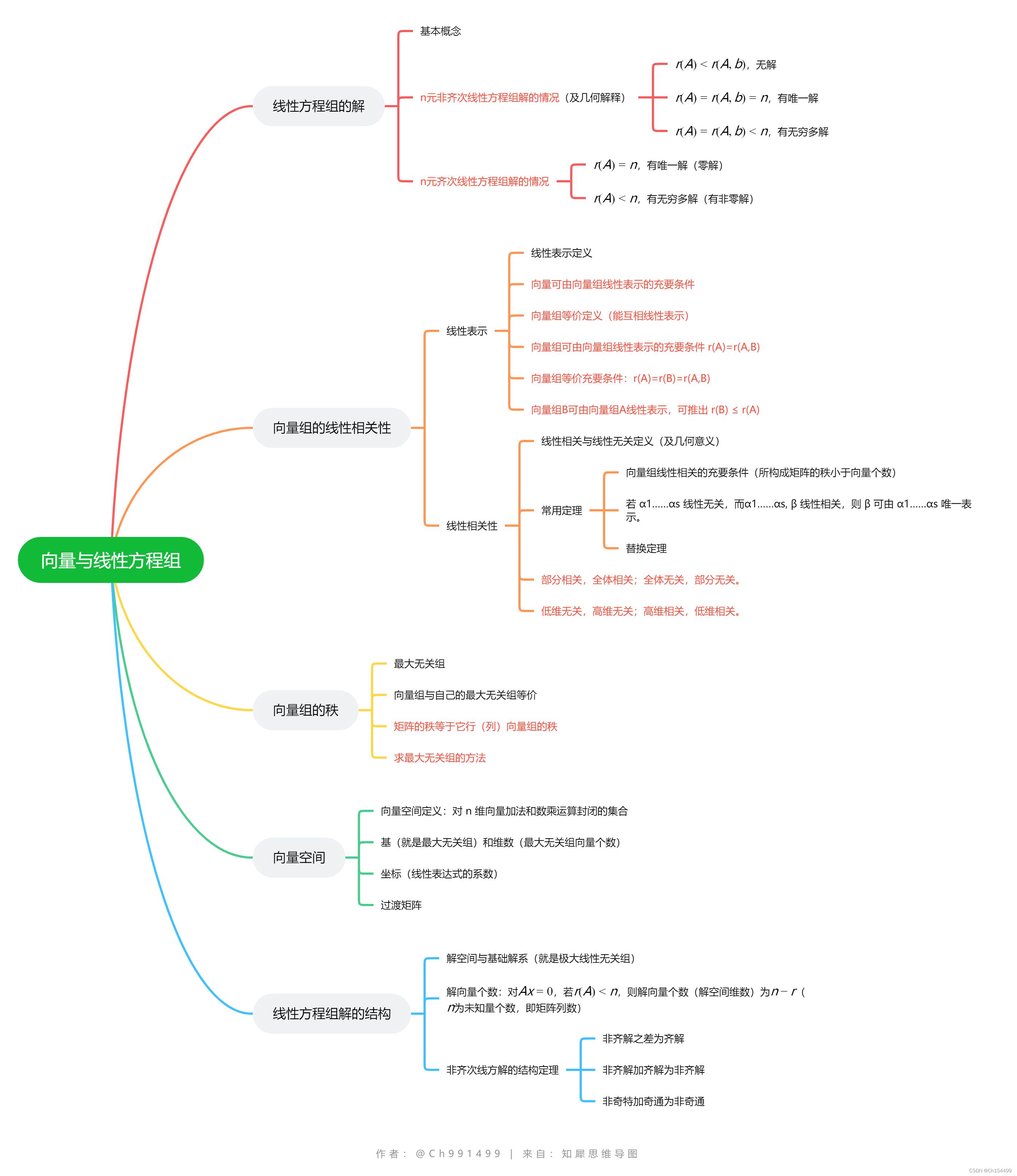
补充:
- 零向量可由任意向量表示。
- 向量组中任一向量可由向量组表示。
- 任意向量均可由向量 ( 1 , 0 , … , 0 ) , ( 0 , 1 , … , 0 ) … ( 0 , 0 , … , 1 ) … (1,0,…,0),(0,1,…,0)…(0,0,…,1)… (1,0,…,0),(0,1,…,0)…(0,0,…,1)…表示。
- 向量组中两向量成比例,线性相关。
- 含零向量的向量组必相关。
- 一个零向量必相关;一个非零向量必无关。
- “相关长,无关短”原理:
1) 增长原理(判断相关): 若 a 1 , a 2 … a n a_1,a_2…a_n a1,a2…an 线性相关,则 a 1 , a 2 … a n , a n + 1 , … a s a_1,a_2…a_n,a_{n+1},…a_s a1,a2…an,an+1,…as 也线性相关。
2) 截短原理(判断无关):若 a 1 , a 2 … a n a_1,a_2…a_n a1,a2…an 线性无关,则 a 1 , a 2 … a n − s ( 0 < s < n ) a_1,a_2…a_{n-s} (0<s<n) a1,a2…an−s(0<s<n) 也线性无关。
3)可据此记忆结论:部分相关,全体相关;全体无关,部分无关。 - 等价的线性无关组含向量的个数相同。
- 若 a 1 , a 2 … a s a_1,a_2…a_s a1,a2…as 线性无关,则 r ( A ) = s r(A)=s r(A)=s;若 a 1 , a 2 … a s a_1,a_2…a_s a1,a2…as 线性相关,则 r ( A ) < s r(A)<s r(A)<s。
- 向量空间中,零元素和负元素都是唯一的。
- 求向量在某个基中的坐标,就是求线性表达式的系数。
易错点
NULL
题型总结
一、求 A x = b Ax=b Ax=b解的情况
- 步骤:
1)写出增广矩阵。
2)用行变换,将矩阵化为阶梯形(不需要化成行最简)。
3)根据 r ( A ) , r ( A , b ) , n r(A), r(A,b), n r(A),r(A,b),n判断解的情况。
4)若为无穷多解,化为行简化阶梯形。不管零行,非零行的首非零元留在左边,其余元素挪到右边,得到一般解。 - 出题都是一般无穷多解的情况。
- 有未知量的行列式求解时,未知量不能放在分母处(可能为零)
- 齐次方程一定有解。
- 为了方便,齐次方程运算使用系数矩阵,不用增广矩阵。
二、判断向量能否由某个向量组线性表示
- 理论依据:一个向量能由某个向量组线性表示的充要条件是:向量组组成的矩阵的秩等于向量组和要线性表示的向量一起组成的矩阵的秩。
- 解题步骤:
1)不用管给的向量是行向量还是列向量,均将向量组中的向量按列作为方程组的系数,要表示的向量作为右端常数项,写出增广阵。
2)化增广阵为行阶梯形,若 r ( A ) = r ( A , b ) r(A)=r(A,b) r(A)=r(A,b)则可以线性表示。 - 判断两个向量组之间能否线性表示或等价(能互相线性表示),可扩展此方法,将要表示的向量换做要表示的向量组即可。
三、求最大无关组并用其表示其余向量
- 步骤:
1)将向量组按列构成矩阵。
2)只用行变换化为行最简阶梯形。
3)首非零元所在的列的向量就是极大无关组。
4)其余向量,其所在列的元素为线性表示的对应系数,直接对应写出即可。
四、求齐次方程的通解
- 步骤:
1)对系数阵用行变换化为行最简形。
2)非零行的首非零元的 1 1 1留在左边,其余元素挪到右边。得同解方程组。
3)令自由未知量取 ( 1 , 0 , … , 0 ) T , ( 0 , 1 , … , 0 ) T … ( 0 , 0 , … , 1 ) T … (1,0,…,0)^T,(0,1,…,0)^T…(0,0,…,1)^T… (1,0,…,0)T,(0,1,…,0)T…(0,0,…,1)T…,代入同解方程组,得基础解析。
4)基础解系乘以对应的实数(如 k 1 , k 2 ∈ R k_1,k_2∈R k1,k2∈R)之和即为通解。
五、求非其次方程通解
- 理论依据:非其次方程的通解等于非齐次方程的特解加对应的齐次方程的通解。
- 步骤:
1)写出增广阵,只用行变换化为最简形。
2)非零行的首非零元的 1 1 1留在左边,其余的挪到右边。写出非齐次的同解方程组,指出谁是自由未知量(不在左边的)。
3)令自由未知量均取零,得 A x = 0 Ax=0 Ax=0的一个特解。
4)令同解方程组右边常数项均为零,得齐次方程的同解方程组,指出谁是自由量。
5)令自由量取相应值,的得 A x = 0 Ax=0 Ax=0的基础解系。
6)非齐次方程的特解加齐次方程的通解,即为非齐次方程的通解。
其余题型
NULL
方法心得
- 根据方程组 A x = b Ax=b Ax=b 的增广矩阵(行阶梯形)判断解的情况或秩的情况技巧:在行阶梯矩阵下方非零数与零之间画分界线,若该线条在解向量与右端向量之间不拐弯(一条直线过去),则有解( r ( A ) = r ( A , b ) r(A)=r(A,b) r(A)=r(A,b));若拐弯了(先竖再横),则无解( r ( A ) < r ( A , b ) r(A)<r(A,b) r(A)<r(A,b))。
参考资料:
[1]安徽理工大学数学系. 线性代数(第三版修订). 天津:天津科学技术出版社, 2019.
[2]安徽理工大学数学系. 线性代数、概率论与数理统计同步辅导习题(第二版). 天津:天津科学技术出版社, 2016.
[3]张天德. 线性代数习题精选精解. 山东:山东科学技术出版社, 2009.
[4]《线性代数》高清教学视频 “惊叹号”系列 宋浩老师
相关文章:

第三章 向量与线性方程组
引言 题型总结中推荐例题有蓝皮书的题型较为重要,只有吉米多维奇的题型次之。码字不易,如果这篇文章对您有帮助的话,希望您能点赞、评论、收藏,投币、转发、关注。您的鼓励就是我前进的动力! 知识点思维导图 补充&…...
数组题目总结 -- 花式遍历
目录 一. 反转字符串中的单词思路和代码:I. 博主的做法II. 东哥的做法III. 其他做法1补充知识点: IV. 其他做法2 二. 旋转图像思路和代码:I. 博主的做法II. 东哥的做法 三. 旋转图像(逆时针旋转90)思路和代码ÿ…...
)
Android 12.0开机过滤部分通知声音(莫名其妙的通知声音)
1.概述 在12.0的开发产品的时候,有时候在开机的时候会有一些通知的声音,但是由于系统模块太多,也搞不清楚到底是哪个模块发出的通知声音,所以就需要从通知的流程来屏蔽这些通知声音 2.开机过滤部分通知声音(莫名其妙的通知声音)核心代码 frameworks/base/core/java/androi…...

LeetCode-0525
102. 二叉树的层序遍历(中等) 思路:使用hash记录深度 class Solution {public List<List<Integer>> levelOrder(TreeNode root) {if(rootnull)return new ArrayList<>();Map<TreeNode,Integer> deep new HashMap&…...

【Linux 】scp命令
前言 Linux scp 命令用于 Linux 之间复制文件和目录。 scp 是 secure copy 的缩写, scp 是 linux 系统下基于 ssh 登陆进行安全的远程文件拷贝命令。 scp 是加密的,rcp 是不加密的,scp 是 rcp 的加强版。 scp命令 前言一、示例1. 从本地复制到远程2. 从…...

Docker部署yolov5
目录 环境下载源码构建Docker镜像运行docker镜像运行目标检测出现partially initialized module cv2 has no attribute _registerMatType错误出现ImportError: libSM.so.6: cannot open shared object file: No such file or directory错误出现AttributeError: Upsample object…...

如何在 Axios 中去控制 Loading?大有学问!
目录 前言 按钮loading 局部loading 全局loading 前言 loading 的展示和取消可以说是每个前端对接口的时候都要关心的一个问题。这篇文章将要帮你解决的就是如何结合axios更加简洁的处理loading展示与取消的逻辑。 首先在我们平时处理业务的时候loading一般分为三种&#x…...

充电桩检测设备厂家TK4860C交流充电桩检定装置
TK4860系列是专门针对现有交流充电桩现场检测过程中接线复杂、负载笨重、现场检测效率低等问题而研制的一系列高效检测仪器,旨在更好的开展充电桩的强制检定工作。 充电桩检测设备是一款在交流充电桩充电过程中实时检测充电电量的标准仪器,仪器以新能源…...

一文3000字实现基于Selenium+Python的web自动化测试框架
一、什么是Selenium? Selenium是一个基于浏览器的自动化测试工具,它提供了一种跨平台、跨浏览器的端到端的web自动化解决方案。Selenium主要包括三部分:Selenium IDE、Selenium WebDriver 和Selenium Grid。 Selenium IDE:Firefo…...
Android 12系统源码_窗口管理(二)WindowManager对窗口的管理过程
前言 上一篇我们具体分析了窗口管理者WindowManagerService的启动流程,对于WindowManagerService有了一个初步的认识。在此基础上,我本打算应该进一步分析WindowManagerService是如何管理系统中的各种窗口的,然而由于Android系统的架构设计,在分析WindowManagerService之前…...
python3.8,torch1.10.2+cu113、torch-geometric 安装
【1】conda create -n name python=3.8 【2】安装 torch 注意先看可适应的最高cuda版本 https://data.pyg.org/whl/ 版本对应 【3】按照顺序安装torch-geometric: torch-sparse、torch-scatter、torch-cluster、 torch-spline-conv \torch-geometric pip install torc…...
、栈(stack))
堆(heap)、栈(stack)
在程序中,栈和堆是两种非常重要的数据结构。它们都用来存储数据,但是它们的定义略有不同。 栈Stack: 栈是一种线性的数据结构,它以 “后进先出”(LIFO)的方式存储数据。栈中的内存空间在编译时就已经确定,大…...

企业级API网关之典型应用场景
目 录 01 企业面对API与网关的现状 02 APIGW介绍及企业应用场景 03 总结 01 企业面对API与网关的现状 在企业中,进行新的系统/应用/产品开发时,具有周密的流程:从需求分析、设计、开发、测试、发布与验收。所以,一…...

【2023年4月美赛加赛】Z题:The future of Olympics 25页完整论文
【2023年4月美赛加赛】Z题:The future of Olympics 25页完整论文 1 题目 背景 国际奥委会(IOC)正面临着夏季奥运会和冬季奥运会申办数量的减少**[1]**。在过去,举办奥运会的竞争非常激烈,声望也很高。然而,最近,主办…...

Rocket重试机制,消息模式,刷盘方式
一、Consumer 批量消费(推模式) Consumer端先启动 Consumer端后启动. 正常情况下:应该是Consumer需要先启动 consumer.setConsumeMessageBatchMaxSize(10);//每次拉取10条 package quickstart; import java.util.List; import co…...
linux+onenet可视化(图形化步骤)
文章目录 一、ONENET项目搭建1.1 ONENET注册1.2 创建产品与设备1.3 添加数据流 二、可视化配置 OneNET是由中国移动打造的PaaS物联网开放平台。平台能够帮助开发者轻松实现设备接入与设备连接,快速完成产品开发部署,为智能硬件、智能家居产品提供完善的物…...

汇编的基础
原视频 基础篇:1.1编程环境的安装 打开DOSBox 0.74-3 Options.bat调整窗口大小 windowresolution1200x640 outputddrawmount c D:\masm c: debugDEBUG 用Debug的R命令查看、改变CPU寄存器的内容: 用Debug的D命令查看内存中的内容: 用Debu…...
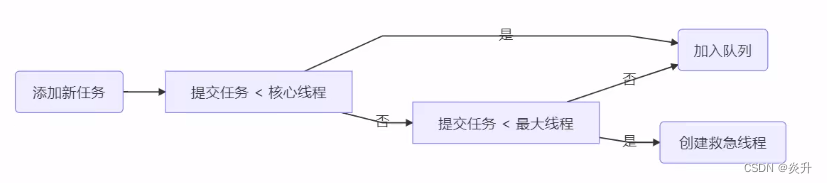
并发编程学习(十四):tomcat线程池
1、Tomcat 功能组件结构 Tomcat 的核心功能有两个,分别是负责接收和反馈外部请求的连接器 Connector,和负责处理请求的容器 Container。 其中连接器和容器相辅相成,一起构成了基本的 web 服务 Service。每个 Tomcat 服务器可以管理多个 Servi…...

简洁灵活工单管理系统,支持工单模版字段、工单状态自定义
一、开源项目简介 本项目为FeelDesk工单管理系统的开源版(OS),是基于开发者版(DEV)分离的标准版;支持工单模版字段、工单状态等自定义,可为不同的模版设置不同的路由规则;对工单需求…...
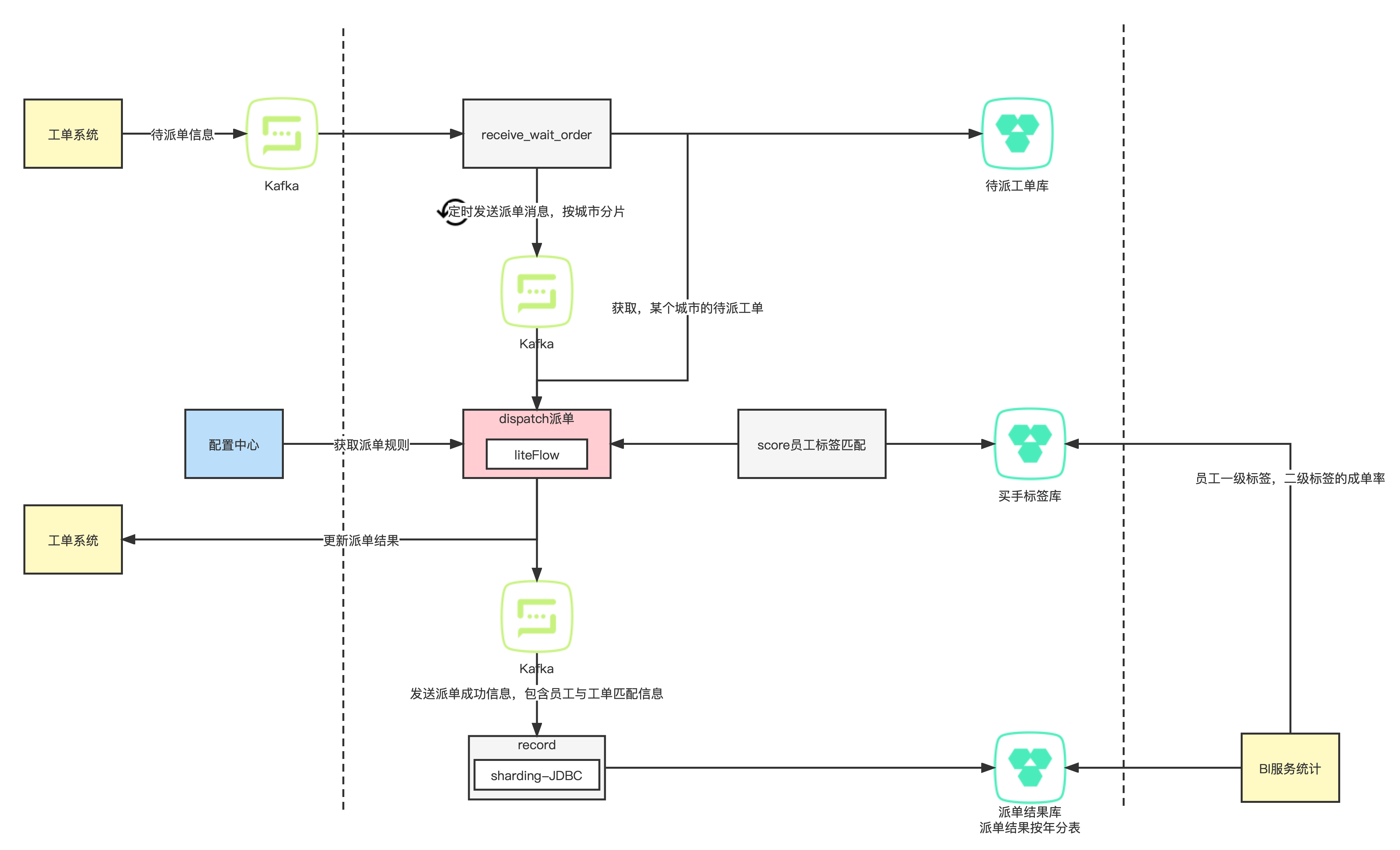
标签派单系统架构设计
需求描述 项目背景 根据员工历史成单情况,计算员工对不同类型工单的转化能力。根据员工和工单标签匹配进行派单。 业务流程图 规则描述 每10分钟,分城进行一次派单,派单规则可能会动态删减,需要支持动态配置 工单标签说明 一…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
