Tree 底层源码实现(二叉树、递归、迭代)
树(Tree)是一种非线性数据结构,由一组节点和它们之间的边组成。在树中,每个节点都有零个或多个子节点,除了根节点外,每个节点都有且仅有一个父节点。树可以被用于许多应用程序,如文件系统、XML文档、数据库索引和编译器语法树等。
二叉树
Java中的树可以通过节点类(Node Class)来实现,这个类通常包含节点的值、指向子节点的指针以及其他一些属性。
下面是一个示例代码,它实现了一个二叉树(Binary Tree):
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }
}
在这个示例中,TreeNode类包含一个整数值(val),以及左右子树的指针(left和right)。为了实现不同类型的树,可以在节点类中添加其他属性。
下面是一个示例代码,它实现了一个二叉搜索树(Binary Search Tree):
class BSTNode {int val;BSTNode left;BSTNode right;BSTNode(int x) { val = x; }
}class BinarySearchTree {BSTNode root;public BinarySearchTree() {root = null;}public void insert(int value) {root = insert(root, value);}private BSTNode insert(BSTNode node, int value) {if (node == null) {return new BSTNode(value);}if (value < node.val) {node.left = insert(node.left, value);} else if (value > node.val) {node.right = insert(node.right, value);}return node;}
}
在这个示例中,BinarySearchTree类是一个包含BSTNode节点的根节点的类。insert方法用于将值插入到树中。在这个实现中,如果要插入的值小于节点的值,则将值插入左子树中;如果要插入的值大于节点的值,则将值插入右子树中。如果节点为空,则将新值插入该位置。
递归方法
在Java中,树的实现可以使用递归方法(Recursion)或者迭代方法(Iteration)。下面是一些关于树的递归方法的示例代码:
前序遍历(Preorder Traversal)
public void preOrderTraversal(TreeNode root) {if (root != null) {System.out.print(root.val + " ");preOrderTraversal(root.left);preOrderTraversal(root.right);}
}
中序遍历(Inorder Traversal)
public void inOrderTraversal(TreeNode root) {if (root != null) {inOrderTraversal(root.left);System.out.print(root.val + " ");inOrderTraversal(root.right);}
}
后序遍历(Postorder Traversal)
public void postOrderTraversal(TreeNode root) {if (root != null) {postOrderTraversal(root.left);postOrderTraversal(root.right);System.out.print(root.val + " ");}
}
以上方法都是通过递归实现的,它们在遍历树时将节点的值打印到控制台。在这些示例代码中,如果节点为空,则返回。
迭代方法
除了递归方法之外,Java中还可以使用迭代方法实现树的遍历。下面是一个示例代码,它实现了二叉树的中序遍历(Inorder Traversal):
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {while (curr != null) {stack.push(curr);curr = curr.left;}curr = stack.pop();res.add(curr.val);curr = curr.right;}return res;
}
在这个示例中,我们使用一个栈(Stack)来保存节点。当当前节点不为空时,将其压入栈中,并将当前节点更新为其左子节点。当当前节点为空时,弹出栈顶元素并将其值添加到结果列表中,然后将当前节点更新为其右子节点。通过不断重复这个过程,我们可以得到二叉树的中序遍历。
相关文章:
)
Tree 底层源码实现(二叉树、递归、迭代)
树(Tree)是一种非线性数据结构,由一组节点和它们之间的边组成。在树中,每个节点都有零个或多个子节点,除了根节点外,每个节点都有且仅有一个父节点。树可以被用于许多应用程序,如文件系统、XML文…...
家政服务小程序实战教程13-接入客服
小程序在微信里使用,以其无需安装随用随走为特点。但是有个问题是,如果提供商品或者服务的,用户如果有问题往往希望平台的运营方给出专业的解答。为了满足这类需求,就需要我们提供客服接入的功能,用户可以点击客服图标…...
大白话高并发(三)
背景 高并发得第三篇,讲一讲压测吧,因为我的目的是模拟100万人同时来秒杀。 是不是真的要找100万个人 没必要 ,你就算100万人掐着表在同一毫秒内把请求请求某一台机器,服务器也不可能在同一时间处理那么多请求,因为…...

vue全家桶(四)前端工程化
vue全家桶(四)前端工程化1.模块化的相关规范1.1模块化概述1.2模块化的分类A.浏览器端的模块化B.服务器端的模块化C.ES6模块化1.2.1 Node.js中通过bable体验ES6模块化1.2.2 ES6模块化的基本语法1.2.2.1 默认导出与默认导入1.2.2.2 按需导出与按需导入1.2.…...
)
超螺旋滑模控制(STA)
超螺旋滑模控制(Super Twisting Algorithm, STA) 超螺旋滑模控制又称超扭滑模控制,可以说是二阶系统中最好用的滑模控制方法。 系统模型 对于二阶系统可以建立具有标准柯西形式的微分方程组 {x˙1x2x˙2fg⋅u\begin{cases} \dot x_1 x_2 \\ \dot x_2 f g \cdo…...

NX二次开发编译时dll自动数字签名及拷贝
前言 在UG5.0开始,所有基于UG二次开发的DLL都要“签名”后才能被客户端上正版的NX调用。 一、基于C# 开发签名 1、添加资源文件 (1)项目类库上右键–>属性–>资源–>添加资源右边小三角–>添加现有文件–>切换到UG安装目录下…...

教你如何搭建人事OA-薪资管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建人事OA-薪资管理。1.2、应用场景根据设置薪资基础及考勤和绩效的数据计算得到各个员工工资详情。2、设置方法2.1、表单搭建1)新建表单【工资表】,字段设置如下;名称类型名称类型人员资料分…...
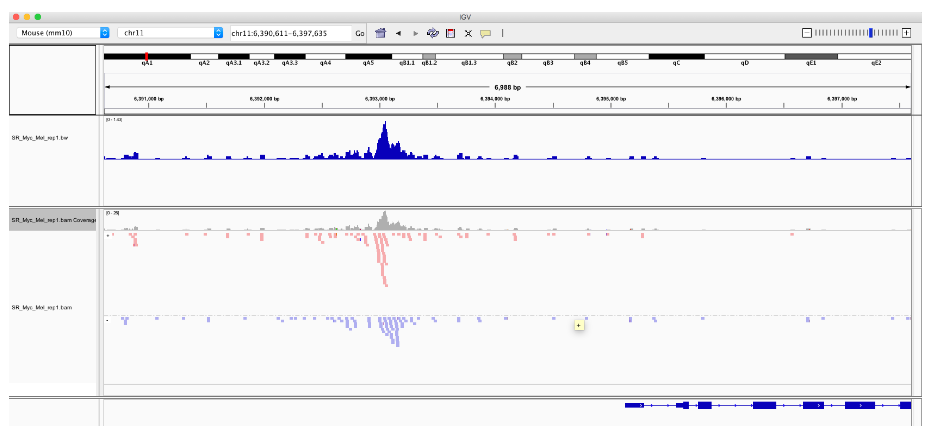
ChIP-seq 分析:Mapped 数据可视化(4)
1. Mapped reads 现在我们有了 BAM 文件的索引,我们可以使用 idxstatsBam() 函数检索和绘制映射读取的数量。 mappedReads <- idxstatsBam("SR_Myc_Mel_rep1.bam")TotalMapped <- sum(mappedReads[, "mapped"])ggplot(mappedReads, aes(x…...
Jenkins 基于Kubernetes 弹性构建池
流程:创建Jenkins Agent;获取Jenkins Agent的参数;渲染yaml模板;调用K8s API在固定的NS中创建一个Pod;运行Jenkins pipeline到agent;创建Agentimport hudson.model.Node.Mode import hudson.slaves.* impor…...

经典算法题---链表奇偶重排(好题)双指针系列
我听别人说这世界上有一种鸟是没有脚的,它只能够一直的飞呀飞呀,飞累了就在风里面睡觉,这种鸟一辈子只能下地一次,那一次就是它死亡的时候。——《阿甘正传》这一文章讲解链表的奇偶排序问题,这是一道不难但是挺好的链…...

数据仓库实战
目录1、最佳实战1.1 表的分类1.2 ETL策略1.3 任务调度2、项目实战2.1 项目概述2.2 数据描述2.3 架构设计2.4 环境搭建2.5 项目开发1、最佳实战 1.1 表的分类 维度建模中表的类型:事实表和维度表 事实表又可以分为:事务事实表、周期快照事实表、累积快照…...

GPT系列:GPT, GPT-2, GPT-3精简总结 (模型结构+训练范式+实验)
😄 花一个小时快速跟着 人生导师-李沐 过了一遍GPT, GPT-2, GPT-3。下面精简地总结了GPT系列的模型结构训练范式实验。 文章目录1、GPT1.1、模型结构:1.2、范式:预训练 finetune1.3、实验部分:2、GPT-22.1、模型结构2.2、范式:预…...

ASE12N65SE-ASEMI高压MOS管ASE12N65SE
编辑-Z ASE12N65SE在ITO-220AB封装里的静态漏极源导通电阻(RDS(ON))为0.68Ω,是一款N沟道高压MOS管。ASE12N65SE的最大脉冲正向电流ISM为48A,零栅极电压漏极电流(IDSS)为10uA,其工作时耐温度范围为-55~150摄氏度。ASE…...
)
centos8防火墙命令配置(开放端口)
查看防火墙状态:(root用户)firewall-cmd –state启动防火墙:(root用户)systemctl start firewalld.service查看防火墙开放端口:(root用户) firewall-cmd --list-ports …...

Instagram营销教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Instagram营销初学者教程 - 从简单和简单的步骤学习Instagram营销从基本到高级概念,包括概述,业务战略,安装和注册,发布和参与,活动审查,微调内容,营销工具和应用程序,集成…...

HTTP Code含义
HTTP Code描述详细100继续100(继续)状态代码表示一个已收到请求,尚未被拒绝服务器。服务器打算在请求已完全收到并已采取行动。当请求包含 Expect 标头字段时100-continue expectation,100响应表示服务器希望接收请求有效负载主体…...
Elasticsearch:Security API 介绍
在我之前的文章 “Elasticsearch:运用 API 创建 roles 及 users” ,我展示了如何使用 Security API 来创建用户及角色来控制访问 Elasticsearch 中的索引。在今天的文章中,我将展示一个使用 Security API 来创建一个用户及角色来访问一个索引…...
springmvc考研交流平台 java ssm mysql
随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,考研交流平台当然也不能排除在外,从备考资料、课程学习的统计和分析,在过程中会产生大量的、各种各样的…...

2.15 vue3 day01 setup ref setup的参数 prop slot插槽 自定义事件通信
二、常用 Composition API 官方文档: 组合式 API 常见问答 | Vue.js 1.拉开序幕的setup 理解:Vue3.0中一个新的配置项,值为一个函数。 setup是所有Composition API(组合API)“ 表演的舞台 ”。 组件中所用到的:数据…...

CentOs7更新Yum源
1.安装wget yum install -y wget 2.备份配置文件 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak 3.下载国内yum源文件(centOs7,比如阿里) wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.al…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
