经典文献阅读之--PIBT(基于可见树的实时规划方案)
0. 简介
作为路径规划而言,不单单有单个机器人自主路径规划,近年来随着机器人行业的兴起,多机器人自主路径规划也越来越受到关注,对于多智能体寻路(MAPF)。一般的操作会给定一个地图、机器人集群、以及它们的初始位置和目的地,MAPF会最终输出一组没有碰撞的路径,用于控制机器人集群完成运动。《Iterative Refinement for Real-Time Multi-Robot Path Planning》文中认为迭代细化MAPF是可取的,原因有三:1)多智能体优化是棘手的,2)次优解可以立即获得,3)在线场景中需要考虑的时间有限,所以要求MAPF是实时规划的。
文中的方案使用次优MAPF求解器来快速获得初始解,然后迭代两个过程:1)选择代理子集,2)使用最优MAPF求解器来优化所选代理的路径,同时保持其他路径不变。由于单个最优求解器只会优化所选代理机器人的路径,因此该方案可以快速生成足够有效的解决方案,同时提供高可伸缩性。相应的代码也在Github上开源了,可以这么说,这套方法还是很有意义的,
1. 文章贡献
- 文中提出了一个通用的框架,基于现有求解器的有效组合可以快速的提供anytimeMAPF求解。 文中的框架首先使用次优MAPF求解器快速获得初始可行解,然后使用最优MAPF求解器找到良好的邻域解。精确地说,该框架通过选择一组代理并使用最优求解器来细化它们的路径,同时保持其他路径固定,迭代地细化解决方案。尽管在细化过程使用了最优求解器,但是每次细化都能快速完成,因为它解决的是一个子问题,其大小取决于选择的代理机器人数量,通常比原问题小得多。我们还提出了合理的候选人,用于选择代理子集。
- 文中研究了在各种基准测试中该方法的有效性,并经验地发现,在小型实例中,该框架在短时间内几乎收敛到最优,并且即使对于非常大的实例(即大环境和/或许多代理)也保持着高效响应。换句话说,它比先前的技术带来了许多实际优势。
- 从更广泛的角度来看,我们的研究也可以被看作是解决一个非常大规模的邻域搜索[24]。更接近我们的概念,Balyo等人[25]研究了针对独立于领域的规划问题的局部重新规划,以优化最长时间。它重复以下操作:创建一个子问题,通过基于SAT的技术获得一个最优子解,并用新的解决方案替换原来的部分解决方案。
2. 主要框架
该框架首先使用次优MAPF求解器获得初始解决方案,然后迭代地细化解决方案的选定部分,即选定代理子集的路径,使用最优MAPF求解器。我们在算法1中给出了伪代码

下面我们来详细的看一下,第1行输入的是次优求解器快速获得初始可行解决方案。在第二行中,我们称所用的次优MAPF求解器为初始求解器。如果初始求解器未能获得解决方案,则框架以失败告终;否则,开始细化,也就是3-6行里面的内容。细化重复以下两个过程,直到中断:
- 使用当前解决方案π [第4行]创建修改集M ⊆ A。
- 使用最优MAPF求解器[第5行]改变M中代理的路径来细化当前解决方案π。我们称这个求解器为细化求解器。细化求解器只改变M中代理的路径;M中代理以外的路径不变。细化继续进行直到中断,例如超时、达到预定迭代次数、不再有改进时、用户中断等。
最终,框架返回最终解决方案[第7行]。
上文中提到的初始求解器可以是任何次优MAPF求解器,只要它能提供可行解即可。作为细化求解器,最好使用从最优求解器改编的版本。改编很简单;让它为M中的代理规划路径,并将其他代理视为动态障碍。例如,对于CBS算法,只为M中的代理求解MAPF,同时禁止低级别搜索使用M中代理以外的所有空间时间对。确切地说,细化求解器并不局限于最优MAPF求解器(可以使用单机器人的求解器)。要求是细化解决方案从原始解决方案不变差。考虑到M中代理以外的路径成本不变,要求是M中代理的路径成本在细化之前和之后都不会增加。
3. 细化求解器性质与要求
下面有一些性质显然是由对细化求解器的要求所设定的。
3.1 定理1(单调性):
对于算法1中的每次迭代,解决方案成本都是不增加的。
一个关键点是细化求解器重新计算所选子集M(一部分机器人)中代理的路径,而不是所有代理的集合A(所有机器人)。与直接使用最优求解器解决原问题相比,细化求解器在每次迭代中解决的问题明显小得多,确保框架即使对于大量代理也是可扩展的。同时下面有几种方法来有效的降低计算的时间。
A.提前终止(早停)
即使细化求解器解决的子问题与原问题相比计算量已经是较小的了,但是如果本身的 ∣ M ∣ |M| ∣M∣仍然太大,细化仍然可能需要很长时间。在这种情况下,最好通过返回当前解决方案来中止当前细化,然后使用新的集合 M M M开始新的迭代。标准可以是超时或使用细化求解器中搜索树大小的阈值。
B.局限性
作为一个限制,该框架可能具有局部最小值,并且没有来自最优解的次优性界限。
命题1(没有次优性界限):考虑最优成本 c ∗ c^* c∗。在算法1中,总是 c ≤ w c ∗ c≤wc^* c≤wc∗,除非将 A A A本身选为修改集 M M M,其中 c c c是每次迭代中的解决方案成本。
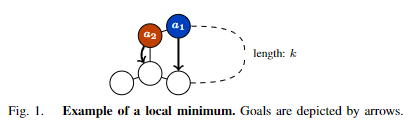
证明:考虑图1中的一个例子。假设初始解决方案将 a 1 a_1 a1分配给顺时针路径(成本: k k k)和 a 2 a_2 a2分配给逆时针路径(成本:1)。当k≥6时,这就不是最优的模型了,因为 a 1 a_1 a1可以采取逆时针路径,并经过 a 2 a_2 a2来移动到目标处(总成本:6)。除非 M ≠ A M ≠ A M=A,否则细化的解决方案不变。假设 w ≥ 1 w≥1 w≥1,使得 c ≤ w c ∗ c≤wc^* c≤wc∗。我们可以取任意 k k k,与 w w w的存在相矛盾。
3.2 定理2(局部最小值存在)
根据初始解决方案,除非将A本身选为M,否则可能无法达到最优解。
注意,当 M = A M = A M=A时,细化求解器必须能够解决原始MAPF问题。
4. 修改集选择
我们从上面可以看到在优化的时候,修改集的选择会影响到整个系统的性能,而如何有效的选择修改集这个就非常重要了。修改集是框架的重要组成部分,其设计会影响计算时间和解决方案质量等性能。本节定义了几个选择规则,以提供合理的候选修改集。
4.1 随机的
一个天真的方法是随机挑选一个代理子集。然后,修改集的大小 M M M就是一个用户指定的参数。需要注意的是,大的 M M M修改有机会在一次迭代中很大程度上降低成本,但由于子问题变得具有挑战性,因此需要花费时间进行细化。
4.2 单一代理
这个规则总是选择一个单一的代理,因为 M M M可以被视为前一个规则(随机)的一个特例。即使只有一个代理,成本也可能因细化而降低。在这种情况下,细化只是一个单一代理的路径寻找问题,可以在没有 M A P F MAPF MAPF求解器的情况下有效地计算出来,例如,通过 A ∗ A^∗ A∗来计算即可,可以简化为一个机器人在其余障碍物(机器人)中规划出来的最优路径。
4.3 着重目标
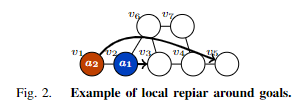
考虑图2中的一个例子。假设当前的解决方案是 π 1 = ( v 2 , v 3 , v 6 , v 3 , v 3 ) π1 = (v2, v3, v6, v3, v3) π1=(v2,v3,v6,v3,v3) 和 π 2 = ( v 1 , v 2 , v 3 , v 4 , v 5 ) π2 = (v1, v2, v3, v4, v5) π2=(v1,v2,v3,v4,v5) 。代理人 a 1 a_1 a1不能实现更短的路径,因为代理人 a 2 a_2 a2在第2个时间步长(第三个值)使用了 a 1 a_1 a1的目标(即v3)。一般来说,对于 a i a_i ai来说,理想成本 d i s t ( π i [ 0 ] , g i ) dist(π_i[0], g_i) dist(πi[0],gi)和实际成本成本 ( a i , π ) (a_i, π) (ai,π)之间存在差距的一个原因可能是另一个代理人 a j a_j aj在时间步骤 t ≥ d i s t ( π i [ 0 ] , g i ) t≥dist(π_i[0], g_i) t≥dist(πi[0],gi)时使用了 a i a_i ai的目标(即 g i g_i gi)。至少在 t t t之前, a i a_i ai不能到达 g i g_i gi并留在那里。在这种情况下,需要联合完善 a i a_i ai和 a j a_j aj的路径。这一观察促使我们创建了一个简单的规则,将当前的解决方案 π π π和一个代理 a i a_i ai作为输入。
4.4 围绕目标的局部修复
这是上一条规则(关注目标)的一个特例。再次假设图2的例子; π 1 = ( v 2 , v 3 , v 6 , v 3 , v 3 ) π1=(v2, v3, v6, v3, v3) π1=(v2,v3,v6,v3,v3), π 2 = ( v 1 , v 2 , v 3 , v 4 , v 5 ) π2 = (v1, v2, v3, v4, v5) π2=(v1,v2,v3,v4,v5)。在聚焦目标(focus-at-goals)中, a 1 a_1 a1的 M M M是 { a 1 , a 2 } \{a_1, a_2\} {a1,a2},因此,细化求解器必须用两个代理解决一个子问题;然而,这种努力可以减少。考虑为 a 1 a_1 a1获得一个更好的路径,忽略 π 2 π_2 π2。在这个例子中,通过目标周围的局部修复获得一条新的路径,不需要搜索; ( v 2 , v 3 , v 3 , v 3 , v 3 ) (v2, v3, v3, v3, v3) (v2,v3,v3,v3,v3)。接下来,为 a 2 a_2 a2计算一条路径,同时避免与这条新路径和其他代理的路径发生碰撞。如果两条新路径的成本之和小于原始路径,就用新路径替换 π 1 π_1 π1和 π 2 π_2 π2。由于搜索工作量减少,预计细化工作会更快完成。一般来说,当 π i = ( . . . , g i , v , g i , . . . , g i ) π_i=(...,g_i,v,g_i,...,g_i) πi=(...,gi,v,gi,...,gi),其中 v ≠ g i v ≠ g_i v=gi,而另一个代理 a j a_j aj在该时间步长使用 g i g_i gi时,可以应用这一规则。
4.5 使用MDD
给定一个单一的路径成本 c c c,从 π i [ 0 ] π_i[0] πi[0]到 g i g_i gi的一组路径可以紧凑地表示为一个多值决策图(MMDD)[35];一个有向无环图,其中一个顶点是一对位置 v ∈ V v∈V v∈V和一个时间步长 t ∈ N t∈N t∈N。
- 在该时间段从起点出发的可达位置;
- 从该时间段到目标的可达位置。
让MDDc i是一个成本为 c c c的 a i a_i ai的MDD,图3显示了两个例子。 M D D 1 2 MDD^2_1 MDD12和 M D D 1 3 MDD^3_1 MDD13。MDD在MAPF求解器中经常使用[28], [36]。
…详情请参照古月居
相关文章:

经典文献阅读之--PIBT(基于可见树的实时规划方案)
0. 简介 作为路径规划而言,不单单有单个机器人自主路径规划,近年来随着机器人行业的兴起,多机器人自主路径规划也越来越受到关注,对于多智能体寻路(MAPF)。一般的操作会给定一个地图、机器人集群、以及它们的初始位置和目的地&am…...

SAP-MM-计算方案字段解析
01、 “步骤”:标识此条件类型在计算方案中的顺序编号,此编号会影响到后续业务中条件类型的排序,不同条件类型之间的编号最好间隔大一些,这样设置便于以后对计算方案进行扩展; 02、 “计数器”࿱…...

go-gf框架两个表以事务方式写入示例
下面是对每一行代码的中文解释: // 创建数据库连接对象 var tx gdb.TX这行代码声明了一个名为tx的变量,类型为gdb.TX,表示数据库事务对象。 // 开启事务 if tx, err g.DB().Ctx(ctx).Begin(ctx); err nil {这行代码通过在数据库连接&…...

2023-5-31第三十一天
conform顺从,遵从,一致 squeeze挤压 proprietary专卖权,专利的,所有的 endeavor努力,尽力 comprise由...组成,包含 compose组成,写作 compact小型的 consult咨询,查阅 expan…...
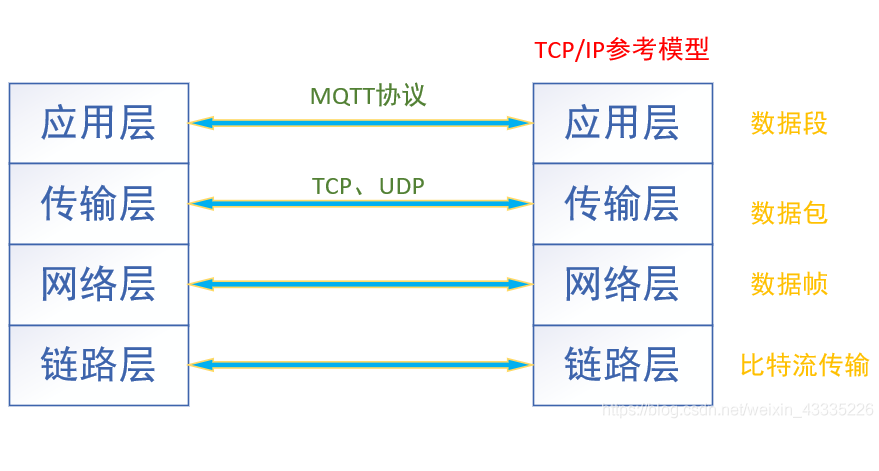
什么是MQTT?mqtt协议和http协议区别
摘要: 什么是MQTT?MQTT(Message Queuing Telemetry Transport)译为:消息队列遥测传输,是一种轻量级的通讯协议,用于在网络上传输消息。MQTT 最初由 IBM 发布,后来成为 OASIS…...
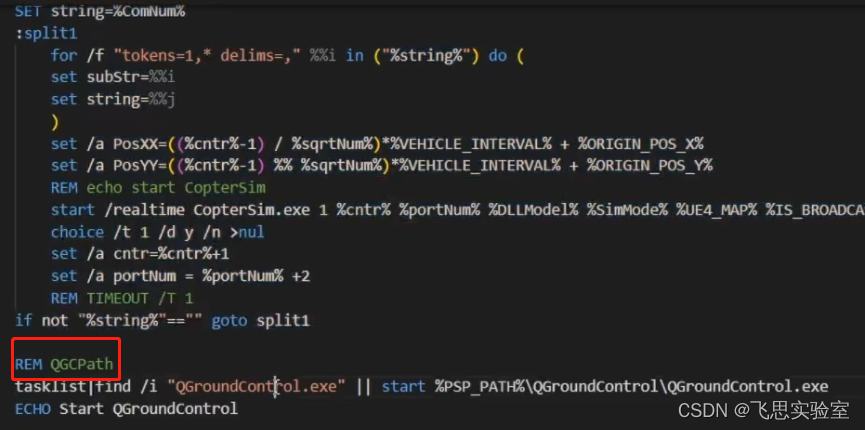
平台使用篇 | 批处理(bat)脚本使用教程(四)
导读 一个开启多机软件在环仿真的批处理文件 (对应卓面RflyTools文件夹中SITLRun快捷方式),双击它,输入想要生成的飞机数量,即可生成多机软件在环仿真,等待RflySim3D显示3DFixed 4/4,然后可通过QGC控制飞机起飞。运行…...

接口的讲解
在这里之前我想童鞋们都学习过了springmvc。mybatis-plus。Springboot等一些框架 那么下面我们就整合这些框架 我们通过写crud这些接口 写接口的第一步就是引入pom文件 在pom文件里引入一下几种依赖 引入父级工程 thymeleaf导入模版工具类 SpringMVCjar包文件 热部署工具 l…...
G0第21章 :gin框架介绍、RESTful API、Gin渲染
G0第21章 :gin框架 01 内容介绍 https://gin-gonic.com/zh-cn/docs/ web本质 Web是基于HTTP协议进行交互的应用网络Web就是通过使用浏览器/APP访问的各种资源 package mainimport ("fmt""net/http" )func sayHello(w http.ResponseWriter, r…...

python list,dict操作
一、list 操作 Python中的列表是一种有序、可变的数据类型,可以存储任意类型的数据。以下是Python中常用的列表操作: 创建列表:使用[]或list()函数创建一个空列表,或者使用[value1, value2, ...]创建一个包含初始值的列表。 访问…...

我有一个页面a,在页面a中调用了一个组件,然后组件中要切换页面a的一块区域,该怎么实现?
你可以在组件中使用路由的编程式导航,通过访问路由实例来切换页面a的对应区域。具体来说,你可以先在页面a中设置一个具有唯一标识的占位符元素,然后在组件中通过路由实例访问这个元素并修改其内容或样式来实现区域切换。路由的编程式导航可以…...

ChatGPT唤醒AI游戏:AIGC持续走深,游戏或成AI最佳抓手
随着人工智能技术的不断发展,AI在游戏行业的应用日益深入。本文将详细探讨ChatGPT在AI游戏领域的应用,以及游戏如何成为AI技术的最佳抓手。让我们一起探讨这个有趣且充满潜力的领域。 一、引言 人工智能在各行各业都取得了巨大的成功,而游戏…...

远程服务和web服务和前端,三方通过socket和websocket进行双向通信传输数据
1. 什么是socket? 在计算机通信领域,socket 被翻译为“套接字”,它是计算机之间进行通信的一种约定或一种方式。通过 socket 这种约定,一台计算机可以接收其他计算机的数据,也可以向其他计算机发送数据。 2. 什么是websocket?…...
Linux 网络基础(2)应用层(http/https协议、请求格式、响应格式、session、cookie、加密传输)
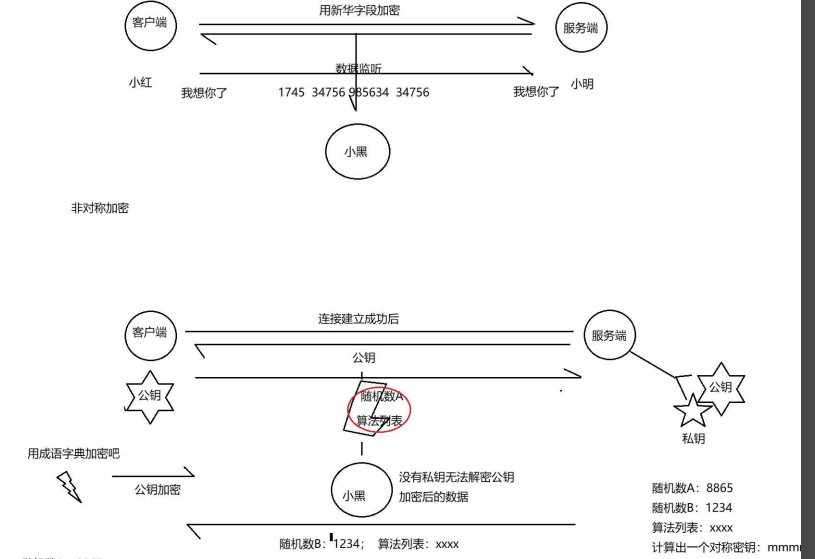
说明:网络基础2讲解的是应用层的典型协议, 通过对于典型协议的理解,来体会数据的网络传输的软件层面的流程与原理。 面试中网络通信相关问题占了很大的比重,而网络通信相关的问题大多都集中在网络基础2这个单元中 下面是应用层的位…...

解决sshfs挂载报错
使用ssh命令和sshfs命令报错 read: Connection reset by peer rootjiangcheng01:~/common/remote# sshfs -o allow_other htrdxxx.xxx.xxx.xxx:/home/htrd /root/common/remote/dev01 read: Connection reset by peer 报错问题排查,追加命令 -o debug -o sshf s_d…...

由于过多的连接错误而被 MySQL服务器 阻止
Caused by: com.mysql.cj.exceptions.CJException: null, message from server: "Host 10.105.***.** is blocked because of many connection errors; unblock with mysqladmin flush-hosts" 这个错误可能表示当您尝试使用 IP 地址为 "10.105.***.**" 的…...

Go语言实现JDBC
Go语言操作数据库 Go语言提供了关于数据库的操作,包下有sql/driver 该包用来定义操作数据库的接口,这保证了无论使用哪种数据库,操作方式都是相同的; 准备工作: 下载驱动 需要在代码所在文件夹下执行相应的命令 go get github.com/go-sql-driver/mys…...

ubuntu修改环境变量的几种方法
ubuntu修改环境变量的几种方法 有多种方法可以修改Ubuntu系统的环境变量,包括: 临时修改环境变量:在终端中使用export命令可以临时修改环境变量。例如,要将PATH环境变量添加到新目录,可以运行以下命令: …...

基于html+css的图展示95
准备项目 项目开发工具 Visual Studio Code 1.44.2 版本: 1.44.2 提交: ff915844119ce9485abfe8aa9076ec76b5300ddd 日期: 2020-04-16T16:36:23.138Z Electron: 7.1.11 Chrome: 78.0.3904.130 Node.js: 12.8.1 V8: 7.8.279.23-electron.0 OS: Windows_NT x64 10.0.19044 项目…...

数据库基础——5.运算符
这篇文章我们来讲一下SQL语句中的运算符操作。 说点题外话:SQL本质上也是一种计算机语言,和C,java一样的,只不过SQL是用来操作数据库的。在C,java中也有运算符,这两种语言中的运算符和数学中的运算符差距不…...
JMeter 性能测试基本过程及示例
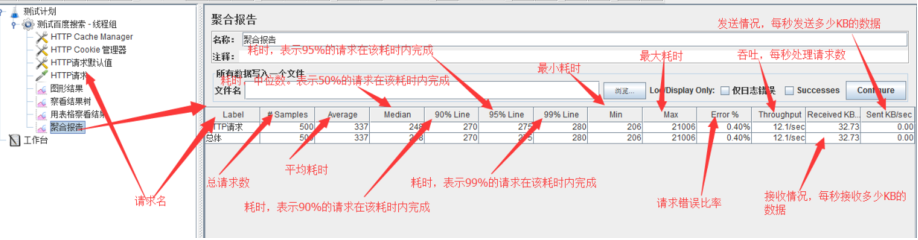
jmeter 为性能测试提供了一下特色: 2023年最新出炉性能测试教程,真实企业性能压测全流程项目实战训练大合集!_哔哩哔哩_bilibili2023年最新出炉性能测试教程,真实企业性能压测全流程项目实战训练大合集!共计11条视频&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
