回溯递归的剪枝模版
题目传送门
主要看灵神的二分模版,如何使用递归实现在 O ( m k ) O(mk) O(mk)时间内,实现对于二分中每个条件的判断。
一般套路:
dfs函数返回值为布尔类型
循环中使用一个dfs,如果其返回true,那么直接这个dfs返回true
技巧:
一个引用类型的值作为终止条件的判断,所有的dfs共享这个变量。
灵神代码:
class Solution {// 返回是否找到 k 个子数组和bool dfs(vector<vector<int>> &mat, int &left_k, int i, int s) {if (i < 0) // 能递归到这里,说明数组和不超过二分的 midreturn --left_k == 0; // 是否找到 k 个for (int x: mat[i]) { // 「枚举选哪个」,注意 mat[i] 是有序的if (x - mat[i][0] > s) // 选 x 不选 mat[i][0]break; // 剪枝:后面的元素更大,无需枚举if (dfs(mat, left_k, i - 1, s - (x - mat[i][0]))) // 选 x 不选 mat[i][0]return true; // 找到 k 个就一直返回 true,不再递归}return false;}public:int kthSmallest(vector<vector<int>> &mat, int k) {int sl = 0, sr = 0;for (auto &row: mat) {sl += row[0];sr += row.back();}// 二分模板 https://www.bilibili.com/video/BV1AP41137w7/int left = sl - 1, right = sr; // 开区间 (sl-1,sr)while (left + 1 < right) { // 开区间不为空// 循环不变量:// f(left) < k// f(right) >= kint mid = left + (right - left) / 2;int left_k = k;if (dfs(mat, left_k, mat.size() - 1, mid - sl)) // 先把第一列的所有数都选上right = mid; // 二分范围缩小至开区间 (left, mid)else // f(mid) < kleft = mid; // 二分范围缩小至开区间 (mid, right)}return right;}
};作者:灵茶山艾府
链接:https://leetcode.cn/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/solutions/2286593/san-chong-suan-fa-bao-li-er-fen-da-an-du-k1vd/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度思考:
为什么回溯的时间复杂度为 O ( m k ) O(mk) O(mk),dfs递归的过程是一棵树从顶到底,本题中如果能够递归到 i < 0 i<0 i<0,那么就是走完了一条路径,该路径花费时间 O ( m k ) O(mk) O(mk)。如果能够成功走完k条路径,那么就直接所有的dfs开始统一返回true,在此之前所有的dfs返回的都是false。
这样做的好处是,虽然每个dfs中的for循环还没结束,但是由于出现了一个true,提前终止了循环,所有就可以保证递归树中每一层的节点个数最多为k个。着实神奇,而且写法十分优雅!
相关文章:

回溯递归的剪枝模版
题目传送门 主要看灵神的二分模版,如何使用递归实现在 O ( m k ) O(mk) O(mk)时间内,实现对于二分中每个条件的判断。 一般套路: dfs函数返回值为布尔类型 循环中使用一个dfs,如果其返回true,那么直接这个dfs返回tru…...

2023-5-30第三十天
effort力气,精力,努力 affect影响,改变,感动 effect结果,效果,影响 worker ampersand &号 asterrisk *号 deal difficulty lose magic proprientary专卖的,所有权 property vow…...

我国中央商务区(CBD)的空间重构及发展模式
中央商务区(Central Business District,简称为CBD),原始意义为“商业会聚之地”是指一个国家或城市商务活动的主要集中的区域,是汇聚商务服务、金融服务、科技服务、咨询服务、会展服务、文化服务等服务业的集聚区域&a…...

Shell脚本的基本例子
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 大数据系列文章目录 目录 定义变量,输出变量输盘输入,执行Lunix命令变量禁止修改变量删除获取传递的变量字符串拼接&…...

C++设计模式介绍与分类
目录 一、设计模式定义 二、设计模式的优点 三、设计模式缺点 四、设计模式中的抽象思维 五、抽象的方法 六、设计模式应用场景 七、设计模式分类 附加知识 (1)C面向对象三种访问修饰符 (2)父类析构函数必须为虚函数 &…...
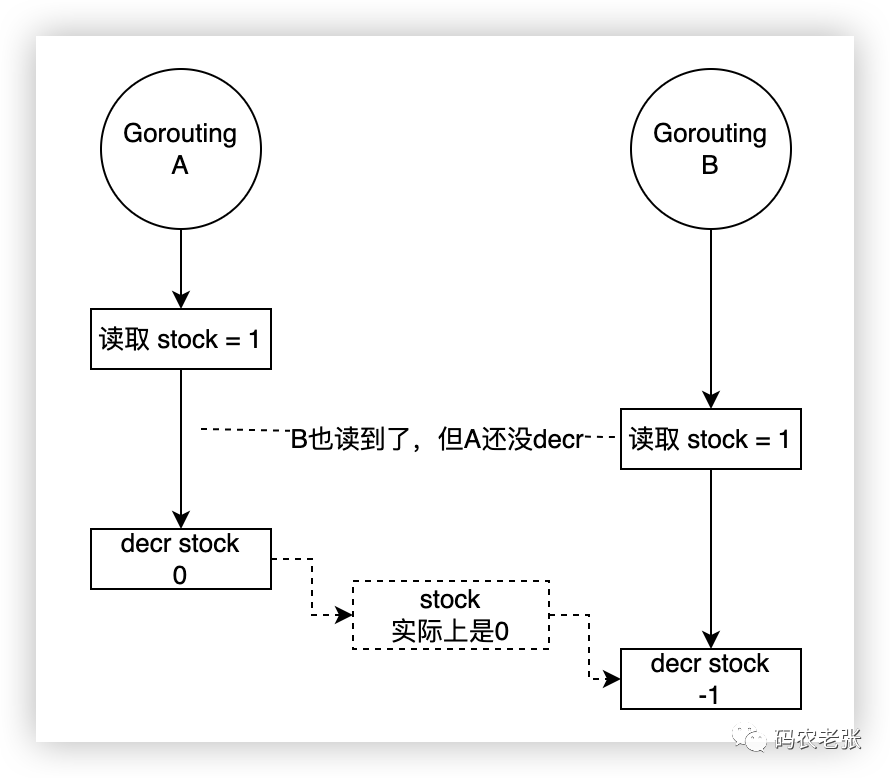
【Redis25】Redis进阶:分布式锁实现
Redis进阶:分布式锁实现 锁这个概念,不知道大家掌握的怎么样。我是先通过 Java ,知道在编程语言中是如何使用锁的。一般 Java 的例子会是操作一个相同的文件,但其实我们知道,不管是文件,还是数据库中的一条…...

【蓝桥杯算法题】输入输出流问题
【蓝桥杯算法题】输入输出流问题 题目:对文本文件进行带缓存的读写操作,可以读取文件不同位置的信息,可以进行对象序列化和对象反序列化。解释:总结: 题目:对文本文件进行带缓存的读写操作,可以…...

BUG提交单模版一
提交人员 XX 提交时间 2005-06-16 产品名称...

Android 12.0系统默认授予读写权限给第三方app
1.概述 在12.0的系统rom定制化开发中, 在6.0以前读写权限是默认授予的,app不需要申请权限 在10.0之前需要android.permission.WRITE_EXTERNAL_STORAGE和android.permission.READ_EXTERNAL_STORAGE 权限就可以了而在安卓11的时候继续强化对SD卡读写的管理,引入了MANAGE_EXTER…...
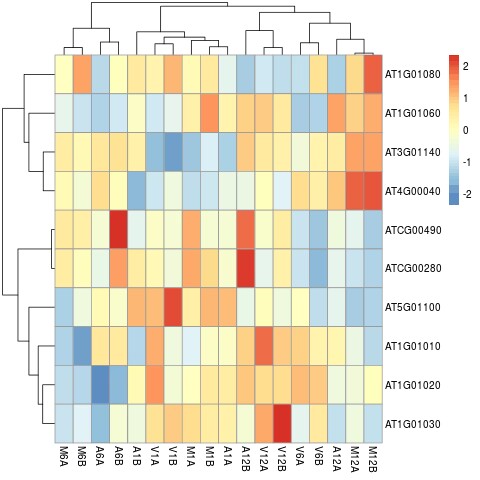
【生信】R语言在RNA-seq中的应用
R语言在RNA-seq中的应用 文章目录 R语言在RNA-seq中的应用生成工作流环境读取和处理数据由targets文件提供实验定义对实验数据进行质量过滤和修剪生成FASTQ质量报告 比对建立HISAT2索引并比对 读长量化读段计数样本间的相关性分析 差异表达分析运行edgeR可视化差异表达结果计算…...
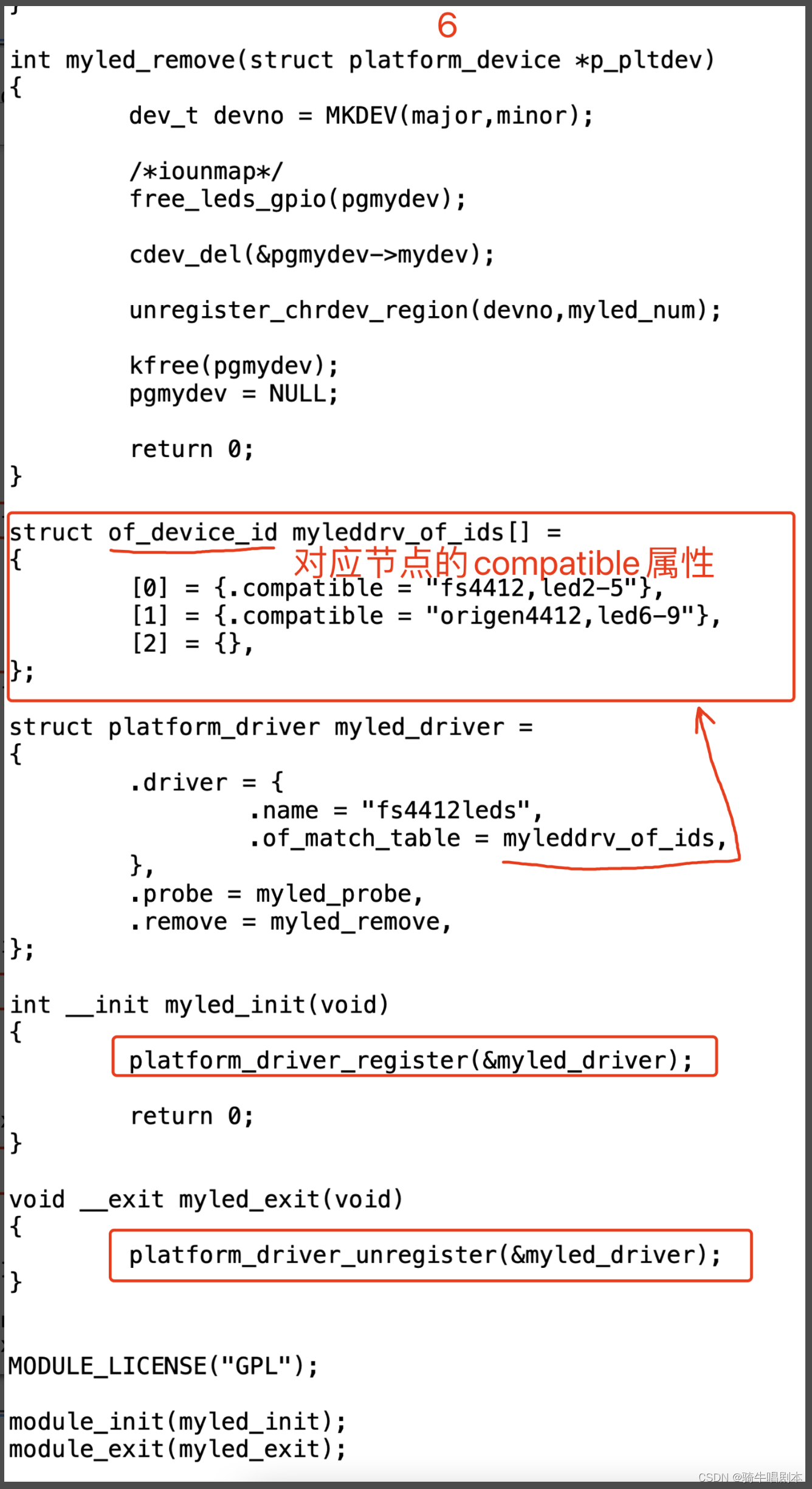
【嵌入式环境下linux内核及驱动学习笔记-(14)linux总线、设备、驱动模型之platform】
目录 1、新驱动架构的导入1.1 传统驱动方式的痛点1.2 总线设备驱动架构 2、platform 设备驱动2.1 platform总线式驱动的架构思想2.2 platform _device相关的数据类型2.2.1 struct platform_device2.2.2 struct platform_device_id2.2.3 struct resource2.2.4 struct device 2.3…...

绝地求生 压q python版
仅做学习交流,非盈利,侵联删(狗头保命) 一、概述 1.1 效果 总的来说,这种方式是通过图像识别来完成的,不侵入游戏,不读取内存,安全不被检测。 1.2 前置知识 游戏中有各种不同的q械…...

云原生技术中的容器技术有哪些?
文章目录 云原生技术中的容器技术有哪些1、云原生的含义2、容器的含义3、云原生的技术的基石:容器技术4、容器技术有哪些? 结语 云原生技术中的容器技术有哪些 在现今的安全行业中云原生安全技术中的容器安全技术有哪些呢,很多用户都不知道具体的含义以…...

Gin中间件的详解 ,用Jwt-go 和 Gin 的安全的登陆的中间件
学习目标: Gin 在不同的group 设置不同的中间件或者过滤器 Gin 的group下的路由上中间件或过滤器 用Jwt-go 和 Gin 的安全的登陆的中间件 JWT 类,它基本有所有基本功能,包括:GenerateToken,GenerateRefreshToken, ValidateToken, ParseToken 学习内容: 1. Gin 在不同的g…...
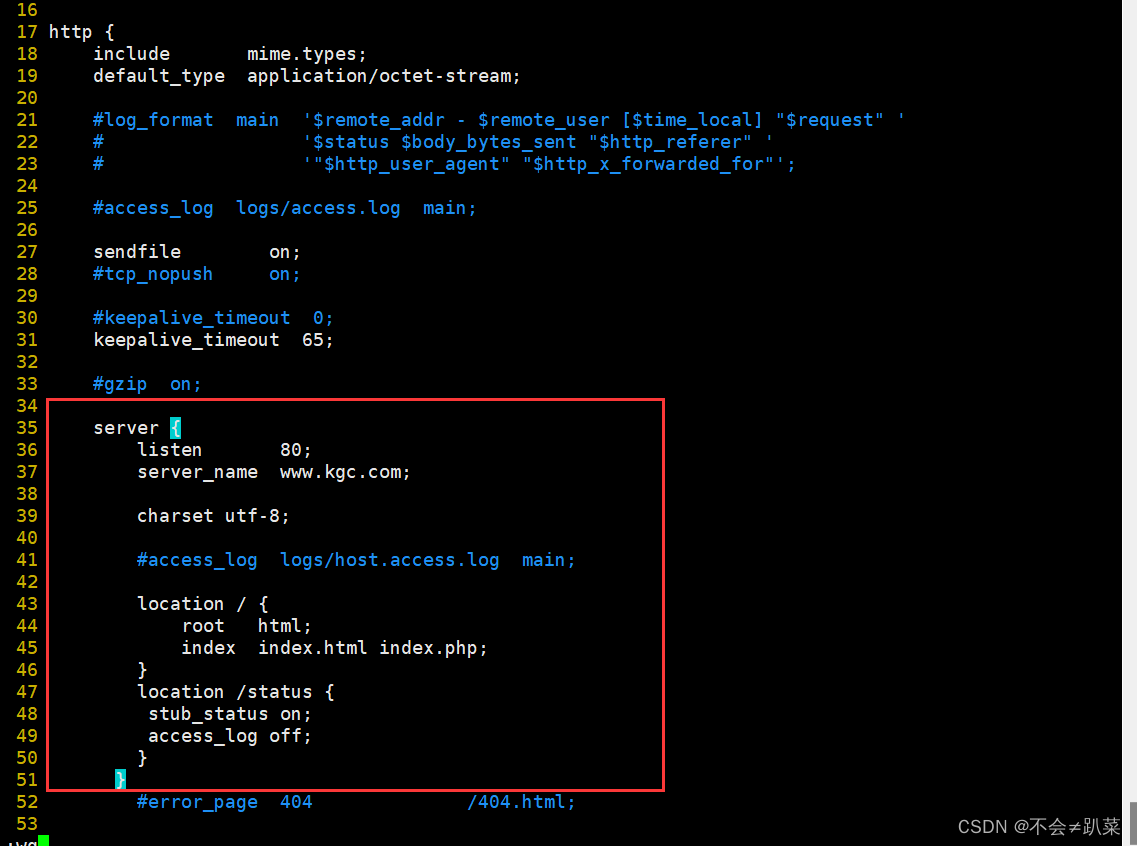
Nginx网站部署
Nginx网站部署 一、访问状态统计配置二、基于授权的访问控制三、基于客户端的访问控制四、基于域名的 Nginx 虚拟主机五、基于IP 的 Nginx 虚拟主机六、基于端口的 Nginx 虚拟主机 一、访问状态统计配置 1.先使用命令/usr/local/nginx/sbin/nginx -V 查看已安装的 Nginx 是否包…...

Hadoop优化
1.小文件 影响: 元数据的瓶颈在于文件的数量,无论单个文件的大小 资源大材小用 优化 计算:使用combininputformat提前合并小文件 JVM重用 存储:归档 2.map端 环形缓冲区-区域大小、溢写比列 提前combinerÿ…...
)
FPGA设计的指导性原则 (中)
1.6基本设计思想与技巧之二:串并转换 串并转换是FPGA设计的一个重要技巧,从小的着眼点讲,它是数据流处理的常用手 段,从大的着眼点将它是面积与速度互换思想的直接体现。串并转换的实现方法多种多样, 根据数据的排序和数量的要求,可以选用寄存器、RAM等实现。前面在乒乓…...

开源创新 协同融合|2023 开放原子全球开源峰会开源协作平台分论坛即将启幕
由开放原子开源基金会主办,阿里云、CSDN 等单位共同承办的开源协作平台分论坛即将于 6 月 12 日上午在北京经开区北人亦创国际会展中心隆重召开。作为 2023 开放原子全球开源峰会的重要组成部分,开源协作平台分论坛将聚焦于开源代码平台的创新功能、用户…...

第四章 相似矩阵与矩阵对角化
引言 题型总结中推荐例题有蓝皮书的题型较为重要,只有吉米多维奇的题型次之。码字不易,如果这篇文章对您有帮助的话,希望您能点赞、评论、收藏,投币、转发、关注。您的鼓励就是我前进的动力! 知识点思维导图 补充&…...

课程11:仓储层Repository实现、AutoMapper自动映射
课程简介目录 🚀前言一、Repository项目1.1创建Repository项目1.2 添加类1.2.1、添加类 RolePermissionRepositiory1.2.2、添加项目引用1.2.3、注入数据库上下文1.3 RolePermissionRepositiory接口的实现二、Repository注入2.1 提取接口2.2 添加项目依赖2.3 项目入口添加依赖…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
