图灵完备游戏：信号计数 解法记录

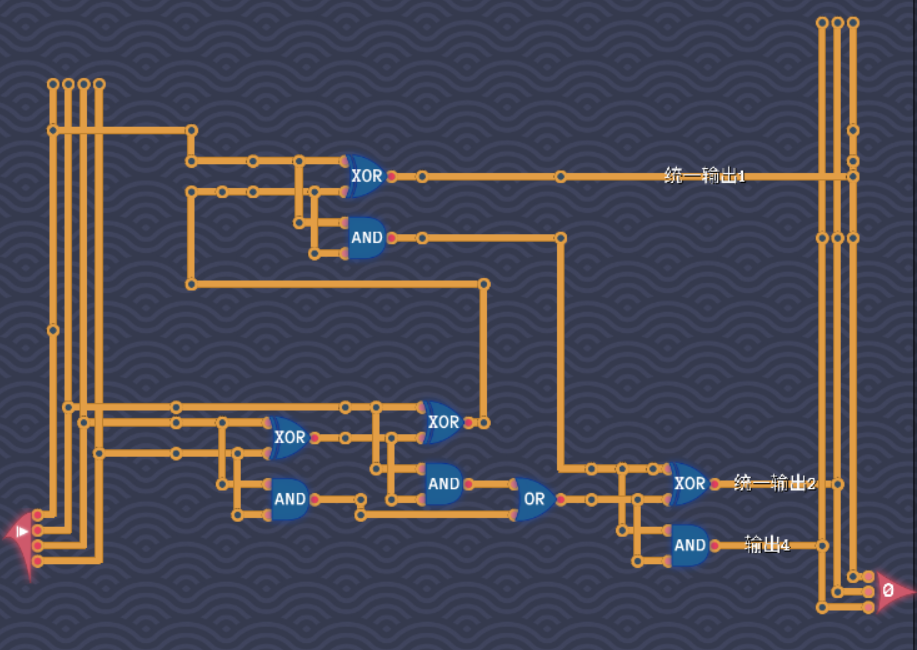
使用1个全加器 + 2个半加器完成。这关的思想主旨在于如何把输出4，输出2，输出1的情况统一在一根导线上。

首先用一个全加器来完成输入2-4这三个引脚的计数，因为全加器输出范围二进制是00 - 11，而输入正好有两个引脚数位是2和1，刚好满足3个输入计数的所有情况。

剩下一个输入需要做分组判断，分为输入1亮的情况和输入1不亮的情况，按计数量分类：

**计数0的情况：**整个电路没有非门，没输入就没有输出，不用管。

**计数1的情况：**分为【输入1亮】和【输入1不亮，输入2-4其中一个亮】的情形。将一个半加器的输入a和电源输入1对接，输入b和下面全加器的s端连接，这样对于情形2，下面全加器的输出端就成为上面半加器的输入了，半加器s端输出1；对于情形1，半加器s端同样输出1，两个情形统一，于是半加器s端正好和终点数位为1的引脚绑定。

**计数2的情况：**分为【输入1亮，输入2-4其中一个亮】和【输入1不亮，输入2-4其中两个亮】的情形，前者有3种情况，后者有C2 3 = 6种情况, 由于我们的全加器s端是上面半加器b端的输入，于是情形1的三种情况全部可以统一为半加器s端输出0，c端输出1, 意思表示就是二进制10 = 2，于是半加器c端和终点数为2的引脚绑定。对于情形2，正好落在全加器的计数范围内，统一为全加器c端输出1，s端输出0，于是全加器c端也可以和终点数为2的引脚绑定，但两个c端都绑定同一个终点就会短路，怎么办呢？这时候第三个半加器就出来了，为方便区分，我们称上方半加器和新加入的半加器分别为半加器1，半加器2，下方全加器称全加器1。

半加器1c端和全加器1c端分别绑定半加器2输入a和输入b，由于计数2情况下，半加器1c端输出1和半加器2c段输出1不可能同时存在，两种情况最终统一为半加器2的s端输出1, 半加器2s端于是可以和终点数位为2的引脚绑定。

计数3的情况： 分为【输入1亮，输入2-4其中两个亮】和【输入1不亮，输入2-4全亮】的情形，情形1是C2 3 = 6种情况，情形2只有1种情况，共7种情况，实际上这里的逻辑是计数1和计数2两个情况的叠加。由于之前计数2和计数1的输出已经被统一了，于是不管那种情况，最终都统一为半加器1s端输出1，c端输出0和半加器2s端输出1，c端输出0的情况。

为什么会这样呢？可以看看，不管是情形1还是情形2，由于输入2-4的输入情况都在两个亮及以上，全加器1的c端输出一定为1，由于全加器1的c端输出是半加器2的b端输入，因此可转化为半加器2的s端输出一定为1，而这个输出正好和数位2引脚绑定。由于全加器1的s端输出又是半加器1b端的输入，因此输入1能够通过半加器1的s端输出来控制终点数位为1引脚的亮暗，

对于情形1，输入1亮，半加器1s端输出1，半加器2的s端输出1，分别点亮数位1和数位2两个引脚，输出3。

对于情形2，全加器s端和c端都输出1，s端输入给半加器1，c端输入给半加器2，于是半加器1s端和半加器2都输出1，分别点亮数位1和数位2两个引脚，输出3。

**计数4的情况：**全加器1s端和c端都输出1，由于全加器1的s端输出是半加器1b端的输入，于是半加器1s端输出0，c端输出1, 半加器1c端输出和全加器1c端输出分别成为半加器2a端和b端的输入，于是半加器2 s端输出0， c端输出1，正好对应计数4的情况，和引脚为4的终点绑定。

码了一个小时的字真不容易。。。。。看看youtube那个硬编码式的解答方案，有点计算机基础真好。。