R7-19 天梯赛团队总分
“天梯赛”的竞赛题目一共有 15 道,分为 3 个梯级:
基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;题目编号相应为L1-X,X取1,2,3,4,5,6,7,8,分别表示基础级的8道题,如L1-1表示基础级的第1题。
进阶级设 4 道题,每道题 25 分,满分为 100 分;题目编号相应为L2-X,X取1,2,3,4,分别表示进阶级的4道题,如L2-2表示进阶级的第2题。
登顶级设 3 道题,每道题 30 分,满分为 90 分。题目编号相应为L3-X,X取1,2,3,分别表示登顶级的3道题,如L3-2表示登顶级的第2题。
注:若对以上表述仍有不理解或者不清楚的,则请参考本套考题的题号与分值。
在我们校赛中,积分规则和正式天梯赛积分规则有些许不同,校赛的积分规则简化后如下:
参赛者须独立按照严格的输入输出要求提交每一题的解题程序。程序须经过若干测试用例的测试,每个测试用例分配一定分数。每题的得分为通过的测试用例得分之和;整场比赛得分为各题得分之和。程序可反复提交,取最高分,提交错误不扣分。
参赛者的个人总分由每题得分和先锋奖励组成。只有当该队员的基础题总分超过 60 分时,其进阶部分的题目分数(包括奖励)才被判为对其个人有效;当其进
阶题总分超过 25 分时,其登顶部分的题目分数(包括奖励)才被判为对其个人有效。
当一支参赛团队的基础题总分超过 300 分时,该队进阶部分的题目分数才被判为对团队有效;只有当其进阶题总分超过 125 分时,该队登顶部分的题目分数才被判为对团队有效。
校赛中每个参赛团队由5名参赛者组成。
注:基础题是默认有效的。对个人/团队无效得分的部分视为0分。
团队的基础题总分为所有队员在基础题的得分总和;
团队的进阶题总分为所有队员在进阶题的得分总和;
团队的登顶题总分为所有队员在登顶题的得分总和。
当队员在进阶题或登顶题的得分对个人来说是无效时,但是这部分仍然计入团队进阶题和登顶题得分,只有当团队基础题得分/进阶题得分达到了进阶条件,团队的进阶题得分/登顶题得分才能被判定为对团队有效。
在竞赛的过程中你和你的队友都如此沉迷,以至于你们都忘记看实时榜单,比赛结束后你们只能通过提交记录计算你们团队每个人的得分以及团队总得分。具有团队精神的你想要亲自编写程序来解决这个问题。
天梯赛是善良的,同一道题你可以多次提交,该题最终得分为多次提交的最高分(参考样例1)。
若有些题没有提交记录,即该题记做0分。
同样因为一股神秘力量(可能来自参赛团队本身 只有自己团队的提交记录),本题不考虑先锋奖励。
输入格式:
输入第一行给出一个非负整数N(0<=N<200),表示提交记录的数量。
接下来N行,每行给出一条提交记录的详细情况,其格式为:队员编号 题目编号 分数。你们队员的编号依次为1,2,3,4,5。
题目保证所有的提交记录只有你们团队的记录,不会出现其他队伍的记录;同时,同一道题可能有多次提交。
输出格式:
一共输出6行。
第1行输出团队总得分。
接下来5行输出团队5个人每个人的成绩,按总分由高到低的顺序。若总分相同,则优先输出编号较小者。
输入样例1:
5
1 L1-1 5
1 L1-1 3
1 L1-1 4
1 L1-1 2
1 L1-1 1
输出样例1:
5
1 5
2 0
3 0
4 0
5 0
输入样例2:
22
1 L1-8 20
1 L1-7 20
1 L1-6 15
1 L1-5 15
2 L1-8 20
2 L1-7 20
2 L1-6 15
2 L1-5 15
3 L1-8 20
3 L1-6 15
3 L1-5 15
4 L1-8 20
4 L1-7 20
4 L1-6 15
4 L1-5 15
4 L1-4 10
4 L1-3 10
1 L1-4 10
1 L1-3 10
1 L1-2 5
5 L2-1 25
5 L2-2 25
输出样例2:
355
1 95
4 90
2 70
3 50
5 0
样例解释2:
5号队员虽然进阶题得到50分,但是他基础题得分为0,所以,对于5号队员个人来说,他的最后总得分为0;对于整个团队来说,团队的基础题部分得分为305,达到了进阶条件;5号选手在进阶部分的得分可以计入团队的进阶部分得分,所以团队最后的总得分为355。接下来请继续你的快乐作答!
模拟题,如果用C++可以在结构体内初始化,自己另写初始化或者分开为多个全局数组也可
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <cstring>
#include <tuple>
#include <cstdlib>
#include <cmath>
#define int long long
#define IOS {std::ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);}
#define end(x) {cout<<x<<endl;return;}
#define endy {cout<<"YES\n";return ;}
#define endn {cout<<"NO\n";return ;}
using namespace std;
void solve();
inline bool cmp(int a,int b);typedef pair<int,int> PII;const int N = 2*1e5+10;
const int null = 0x3f3f3f3f;
struct node {int i;int ti[4*8+10]={0};int ji=0,jin=0,deng=0;int jiang1=0,jiang2=0;int sum=0;
};inline bool cmpnx(node a,node b);
inline bool cmpni(node a,node b);string s;char ch;int n,m,q,i,j,k,x;double d;float f;//int a[N],b[N],h[N];inline bool cmp(int a,int b){return a>b;}
inline bool cmpn(node a,node b){return a.sum>b.sum;}int sum=0;
int sum_deng=0,sum_jin=0;
void solve(){cin>>n;node a[5+1];for(i=1;i<=n;i++){int fen;cin>>x>>s>>fen;a[x].ti[(s[1]-'0')*8+s[3]-'0']=max(fen,a[x].ti[(s[1]-'0')*8+s[3]-'0']);}for(i=1;i<=5;i++){a[i].i=i;for(j=8+1;j<=8+8;j++)a[i].sum+=a[i].ti[j];sum+=a[i].sum;if(a[i].sum>60)for(j=2*8+1;j<=2*8+4;j++)a[i].sum+=a[i].ti[j],a[i].jin+=a[i].ti[j];//,sum_jin+=a[i].ti[j];for(j=2*8+1;j<=2*8+4;j++)sum_jin+=a[i].ti[j];if(a[i].jin>25)for(j=3*8+1;j<=3*8+3;j++)a[i].sum+=a[i].ti[j],a[i].deng+=a[i].ti[j];//,sum_deng+=a[i].ti[j];for(j=3*8+1;j<=3*8+3;j++)sum_deng+=a[i].ti[j];//sum_jin+=a[i].jin;//sum_deng+=a[i].deng;}int ans=sum+sum_jin+sum_deng;if(sum<=300){ans-=sum_jin;sum_jin=0;}if(sum_jin<=125)ans-=sum_deng;cout<<ans<<'\n';stable_sort(a+1,a+5+1,cmpn);for(i=1;i<=5;i++)cout<<a[i].i<<' '<<a[i].sum<<'\n';}signed main(){//IOSint _=1;//cin>>_;while(_--)solve();return 0;
}相关文章:

R7-19 天梯赛团队总分
“天梯赛”的竞赛题目一共有 15 道,分为 3 个梯级: 基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;题目编号相应为L1-X,X取1,2,3,4,5,6,7,8,分别表示基础级的8道题…...

使用 Kotlin 的 Opt-in (选择加入)功能注解API提示当前非稳定API
前言 之前在给公司项目封装库的时候,领导告诉我封装的漂亮一点,等以后公司发展起来了可能需要把这个库提供给第三方接入使用。 此时,就有这么一个问题:某些功能函数使用条件比较苛刻,直接使用可能会出现意想不到的后…...

webpack配置排除打包
webpack配置排除打包 思路 打包时,不要把类似于element-ui第三方的这些包打进来 从网络上,通过url地址直接引入这些包 操作 (1)先找到 vue.config.js, 添加 externals 项,具体如下: config…...

HNU-操作系统OS-ucoreLab系列-感悟
谨以此片篇,献给熬夜的8个晚上,以及逝去的时光。 感悟: 今天结束了所有的Lab实验(2023.6.3),感慨万千。 喜是这个实验终于结束了,悲是其实有好多地方我都没有理解。 应该指出,由于验收的助教学长学姐们的宽容,HNU实际上在验收这一块的要求还是比较低的。 但是这个…...
MySQL运维篇(三)
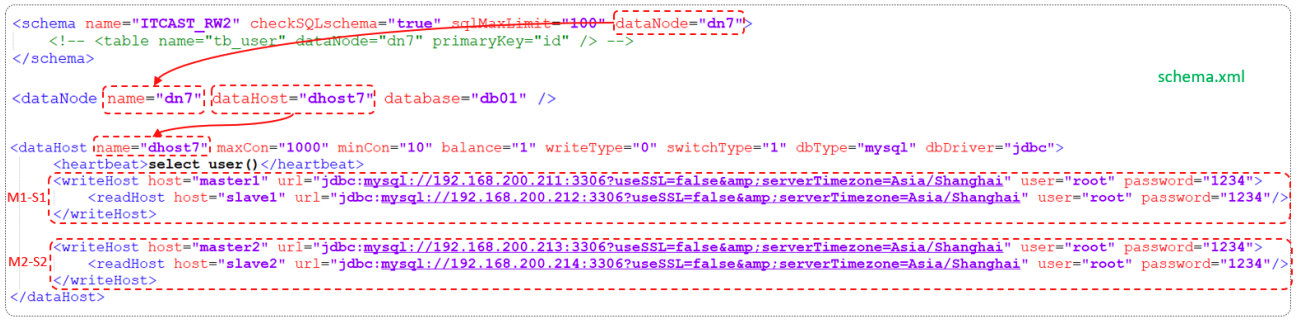
五.读写分离 5.1 介绍 读写分离,简单地说是把对数据库的读和写操作分开,以对应不同的数据库服务器。主数据库提供写操作,从数据库提供读操作,这样能有效地减轻单台数据库的压力。 通过MyCat即可轻易实现上述功能,不仅可以支持MySQL&#x…...

Lecture 2 Text Preprocessing
目录 Some DefinitionsReasons for PreprocessingPreprocessing StepsSentence Segmentation 句子分割Binary Classifier 二元分类器Word Tokenization: English 英文词元标记化Word Tokenization: Chinese 中文词元标记化Word Tokenization: German 德语词元标记化Subword Tok…...
web练习第二周
前言:(博主个人学习笔记,不用看)web练习第二周,仅做出前3题。相比于第一周,难度大幅增加,写题时就算看了wp还是像个无头苍蝇一样到处乱创,大多都是陌生知识点,工具的使用…...
)
LC-1439. 有序矩阵中的第 k 个最小数组和(二分答案、多路归并)
1439. 有序矩阵中的第 k 个最小数组和 难度困难120 给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。 你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。 示例 1:…...

一文1000字从0到1实现Jenkins+Allure+Pytest的持续集成
一、配置 allure 环境变量 1、下载 allure是一个命令行工具,可以去 github 下载最新版:https://github.com/allure-framework/allure2/releases 2、解压到本地 3、配置环境变量 复制路径如:F:\allure-2.13.7\bin 环境变量、Path、添加 F:\…...
)
给一个有序数组生成平衡搜索二叉树(java)
给一个有序数组生成平衡搜索二叉树 给一个有序数组生成平衡搜索二叉树递归生成二叉树专题 给一个有序数组生成平衡搜索二叉树 给定一个有序的数组,用这个数组生成一个平衡搜索二叉树. 这个题还是很简单的,知道什么时平衡搜索二叉树就行了, 左边值小于头节点值,头节点值小于右边…...

【JavaSE】Java基础语法(二十二):包装类
文章目录 1. 基本类型包装类2. Integer类3. 自动拆箱和自动装箱4. int和String类型的相互转换 1. 基本类型包装类 基本类型包装类的作用 将基本数据类型封装成对象的好处在于可以在对象中定义更多的功能方法操作该数据常用的操作之一:用于基本数据类型与字符串之间的…...
javascript基础十八:说说你对JavaScript中事件循环的理解
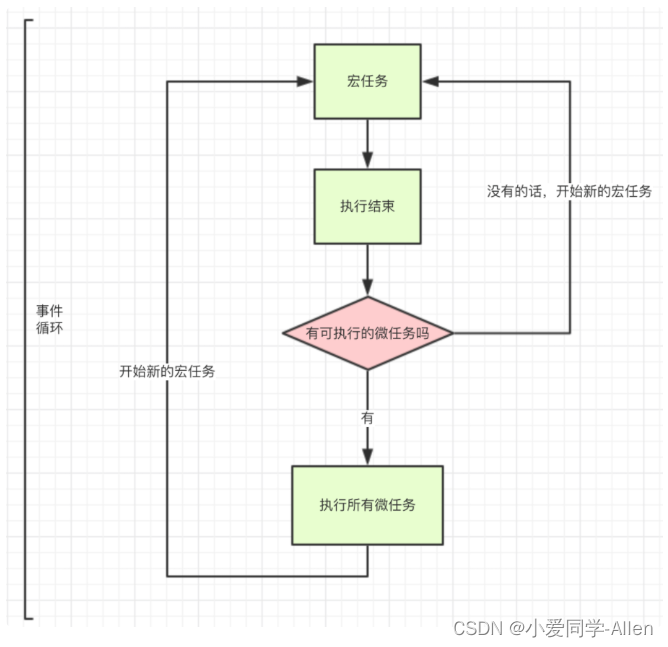
一、是什么 JavaScript 在设计之初便是单线程,即指程序运行时,只有一个线程存在,同一时间只能做一件事 为什么要这么设计,跟JavaScript的应用场景有关 JavaScript 初期作为一门浏览器脚本语言,通常用于操作 DOM &#…...

详解js中的浅拷贝与深拷贝
详解js中的浅拷贝与深拷贝 1、前言1.1 栈(stack)和堆(heap)1.2 基本数据类型和引用数据类型1.2.1 概念1.2.2 区别1.2.3 基本类型赋值方式1.2.4 引用类型赋值方式 2、浅拷贝2.1 概念2.2 常见的浅拷贝方法2.2.1 Object.assign()2.2.…...

Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试
Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试 文章目录 Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试敏捷开发的特征1、迭代式开发2、增量交付3、及时反馈4、持续集成5、自我管理敏捷开发和迭代式开发的根本区别1、性质…...

k8s 维护node与驱逐pod
1.维护node节点 设置节点状态为不可调度状态,执行以下命令后,节点状态会多出一个SchedulingDisabled的状态,即新建的pod不会往该节点上调度,本身存在node中的pod保持正常运行 kubectl cordon k8s-node01 kubectl get node 2.驱…...
SouapUI接口测试之创建性能测试
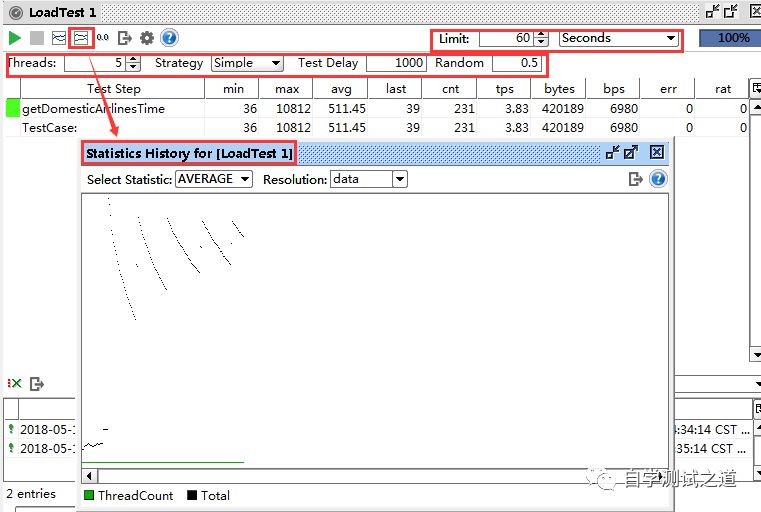
SouapUI也是一个能生动的体现一个系统(项目)性能状态的工具,本篇就来说说如何在SouapUI工具下创建性能测试 一、创建测试用例 由于在《SouapUI接口测试之使用Excel进行参数化》篇已经创建好了测试用例,本篇就不讲解如何创建测试…...
springboot整合kafka入门
kafka基本概念 producer: 生产者,负责发布消息到kafka cluster(kafka集群)中。生产者可以是web前端产生的page view,或者是服务器日志,系统CPU、memory等。 consumer: 消费者,每个consumer属于一个特定的c…...

Rust 笔记:Rust 语言中的字符串
Rust 笔记 Rust 语言中的字符串 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/detail…...

华为OD机试真题 Java 实现【将真分数分解为埃及分数】【牛客练习题】
一、题目描述 分子为1的分数称为埃及分数。现输入一个真分数(分子比分母小的分数,叫做真分数),请将该分数分解为埃及分数。如:8/11 = 1/2+1/5+1/55+1/110。 注:真分数指分子小于分母的分数,分子和分母有可能gcd不为1! 如有多个解,请输出任意一个。 二、输入描述 输…...
Zemax Lumerical | 二维光栅出瞳扩展系统优化
简介 本文提出并演示了一种以二维光栅耦出的光瞳扩展(EPE)系统优化和公差分析的仿真方法。 在这个工作流程中,我们将使用3个软件进行不同的工作 ,以实现优化系统的大目标。首先,我们使用 Lumerical 构建光栅模型并使用…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
