算法基础学习笔记——④前缀和\差分\双指针\位运算
✨博主:命运之光
✨专栏:算法基础学习

目录
✨前缀和
✨一维前缀和
🍓一维前缀和模板:
✨二维前缀和
🍓二位前缀和模板:
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨前缀和
✨一维前缀和
原i:a[1] a[2] a[3] …a[n]
前缀和:s[i]=a[1]+a[2]+…+a[i] s[0]=0(方便处理边界问题)
注:下标一定从1开始
1.如何求s[i]:
for(i=1;i<=n;j++)s[i]=s[i-1]+a[i]2.作用:(快)O(1)
快速求出原数组里一段数的和

🍓一维前缀和模板:
S[i] = a[1] + a[2] + ... a[i]a[l] + ... + a[r] = S[r] -S[l -1]✨二维前缀和


🍓二位前缀和模板:
S[i, j] = 第i行j列格子左上部分所有元素的和。
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] -S[x1 -1, y2] -S[x2, y1 -1] + S[x1 -1, y1 -1]



✨差分
差分实际是前缀和的逆运算
✨一维差分
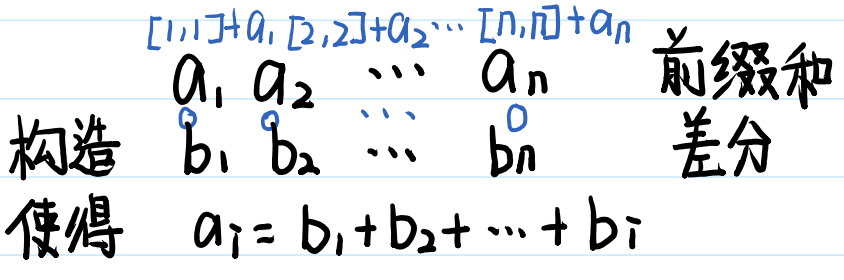

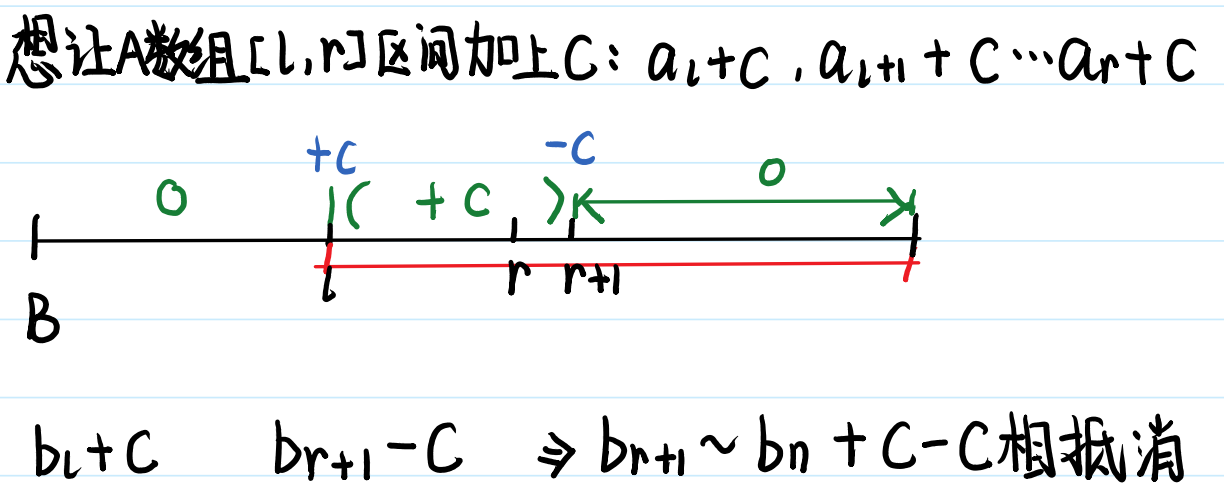
🍓一维差分模板:
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c

✨二维差分

🍓二维差分模板:
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

✨双指针
双指针算法的核心思想:
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
O(n^2)
将上面的朴素算法优化到O(n)

🍓双指针模板:
for (int i = 0, j = 0; i < n; i ++ )
{while (j < i && check(i, j)) j ++ ;// 具体问题的逻辑
}常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
🍓例题:统计日志
#include <iostream>
#include <algorithm>
using namespace std;
const int N=100000+5;
typedef struct Log{
int ts,id;
}Log;
Log logs[N];
//(tk-D,tk]
int n,d,k;
int cnt[N];//cnt[i]始终存储的是连续d分钟内id=i的帖子的点赞量
bool rt[N];
bool cmp(Log qian,Log hou){if(qian.ts<hou.ts)return true;return false;
}
int main(){scanf("%d%d%d",&n,&d,&k);int m=0;for(int i=1;i<=n;i++){scanf("%d%d",&logs[i].ts,&logs[i].id);m=max(m,logs[i].id);}sort(logs+1,logs+n+1,cmp); for(int i=1,j=1;i<=n;i++){//i和j始终维护长度小于d的区间 cnt[logs[i].id]++; while(logs[i].ts-logs[j].ts>=d){cnt[logs[j].id]--;j++;}if(cnt[logs[i].id]>=k){rt[logs[i].id]=true;}}for(int i=0;i<=m;i++){if(rt[i]==true)printf("%d\n",i);}
}🍓例题:统计子矩阵
#include <iostream>
using namespace std;
const int N=510;
int n,m,k;
int s[N][N];
int main(){cin>>n>>m>>k;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>s[i][j];s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+s[i][j];}}long long ans=0;for(int l=1;l<=m;l++){for(int r=l;r<=m;r++){for(int d=1,u=1;d<=n;d++){while(u<=d&&(s[d][r]-s[d][l-1]-s[u-1][r]+s[u-1][l-1]>k))u++;if(u<=d)ans+=d-u+1;}}}cout<<ans<<endl;
}✨位运算
✨操作一
n的二进制中第k位是几

1.先把第k位移到最后一位n>>k
2.看个位是几x&1


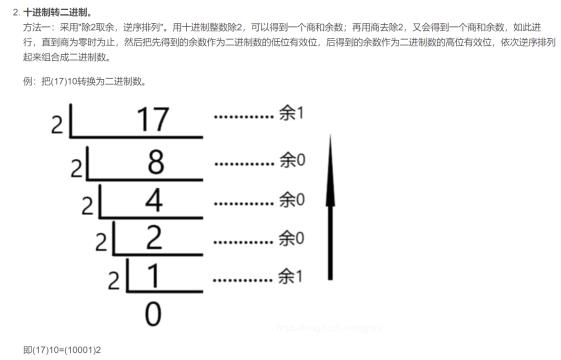
🍓十进制转化成二进制、八进制、十六进制(连除法)

🍓二进制、八进制、十六进制转化成十进制

🍓关于原码,反码,补码:
原码、反码和补码是计算机中用来表示带符号整数的三种编码方式。
1. 原码(Sign-Magnitude):
原码是最简单的表示方法,将一个整数按照正负号和数值进行编码。具体规则如下:
- 正数的原码是其二进制表示形式。
- 负数的原码是将对应的正数的原码最高位改为1。
🍓例如,假设用8位二进制表示整数,数字+3的原码是00000011,数字-3的原码是10000011。
2. 反码(One's Complement):
反码是在原码的基础上,将负数的表示方式进行改进。具体规则如下:
- 正数的反码与其原码相同。
- 负数的反码是将对应的正数的原码按位取反,即将0变为1,将1变为0。
🍓例如,数字+3的反码是00000011,数字-3的反码是11111100。
3. 补码(Two's Complement):
补码是在反码的基础上进行改进,是计算机中最常用的表示方式。具体规则如下:
- 正数的补码与其原码相同。
- 负数的补码是将对应的正数的原码按位取反,然后再加1。
🍓例如,数字+3的补码是00000011,数字-3的补码是11111101。
补码的使用在计算机中具有以下好处:
- 可以统一处理正数和负数的加减运算,无需单独处理符号位。
- 补码只有一个表示零的编码,避免了正零和负零的问题。
- 补码的表示范围比原码和反码更广,能够表示的最大正整数比较大。
🍓🍓需要注意的是,在使用补码表示的计算机系统中,最高位通常被用作符号位,即0表示正数,1表示负数。这种表示方式使得补码能够直接进行加减运算,并且可以方便地检测结果的正负。
相关文章:

算法基础学习笔记——④前缀和\差分\双指针\位运算
✨博主:命运之光 ✨专栏:算法基础学习 目录 ✨前缀和 ✨一维前缀和 🍓一维前缀和模板: ✨二维前缀和 🍓二位前缀和模板: 前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O&a…...
等详解)
【Linux系统基础快速入门详解】Linux下安装软件必知必会4种方法(yum,编译安装,rpm包,二进制方式)等详解
在 Linux 下安装软件有多种方法可供选择,常用的包括 yum、编译安装、rpm 包和二进制方式。下面对这些方法进行详细说明: 使用 yum 安装软件yum 是 Red Hat 系列 Linux 发行版中常用的软件包管理工具,通过 yum 可以方便地安装、升级和删除软件包。yum 默认从官方仓库中下载软…...

ASEMI代理长电可控硅BT136参数,BT136规格,BT136说明
编辑-Z 长电可控硅BT136参数: 型号:BT136 RMS通态电流IT(RMS):6A 非重复浪涌峰值导通电流ITSM:25A 峰值栅极电流IGM:2A 平均栅极功耗PG(AV):0.5W 存储接点温度范围Tstg:-40 to 150℃ 工…...
代码线程安全
线程生命周期 synchronized synchronized会自动释放锁 synchronized同步代码块 synchronized后面括号里obj是锁对象(保证唯一);static修饰的obj对象是自定义MyThread线程类的静态成员变量,该自定义线程类所有实例共享保证锁对象唯一性;另一…...
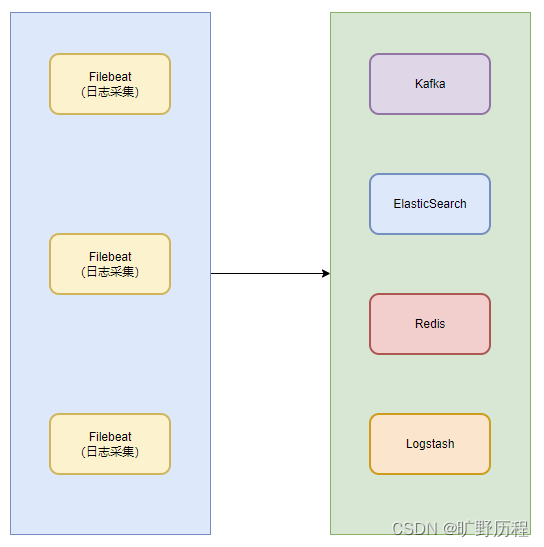
Filebeat技术栈总结
filebeat 是一个轻量型日志采集器,本质上是一个 agent 。不依赖于任何应用,可以安装在任何节点上,可单独使用 Filebeat 并根据配置读取对应位置的日志进行上报和搜集。 filebeat 内置了常用的 output 组件,例如 kafka、ElasticSe…...
健壮性测试工具——Android Monkey)
【App自动化测试】(十六)健壮性测试工具——Android Monkey
目录 1. 介绍2. 安装3. Monkey的使用4. money常用命令5. 常用事件类型参数6. Monkey使用参考 1. 介绍 Monkey是一个在模拟器或设备上运行的程序,用于生成用户事件的伪随机流。 为什么要使用Monkey这个自动化遍历工具? Monkey解决了一个测试痛点ÿ…...

实现第一个内核程序的Hello World
背景 在内核的开发中,总要先入个门。那么就要来编写第一个内核程序 入门 一个 module_init 程序是Linux内核模块的一部分,通过module_init 方法就能将程序载入内核。 module_init 方法需要以下步骤 编写module_init 的代码,并将其保存为…...
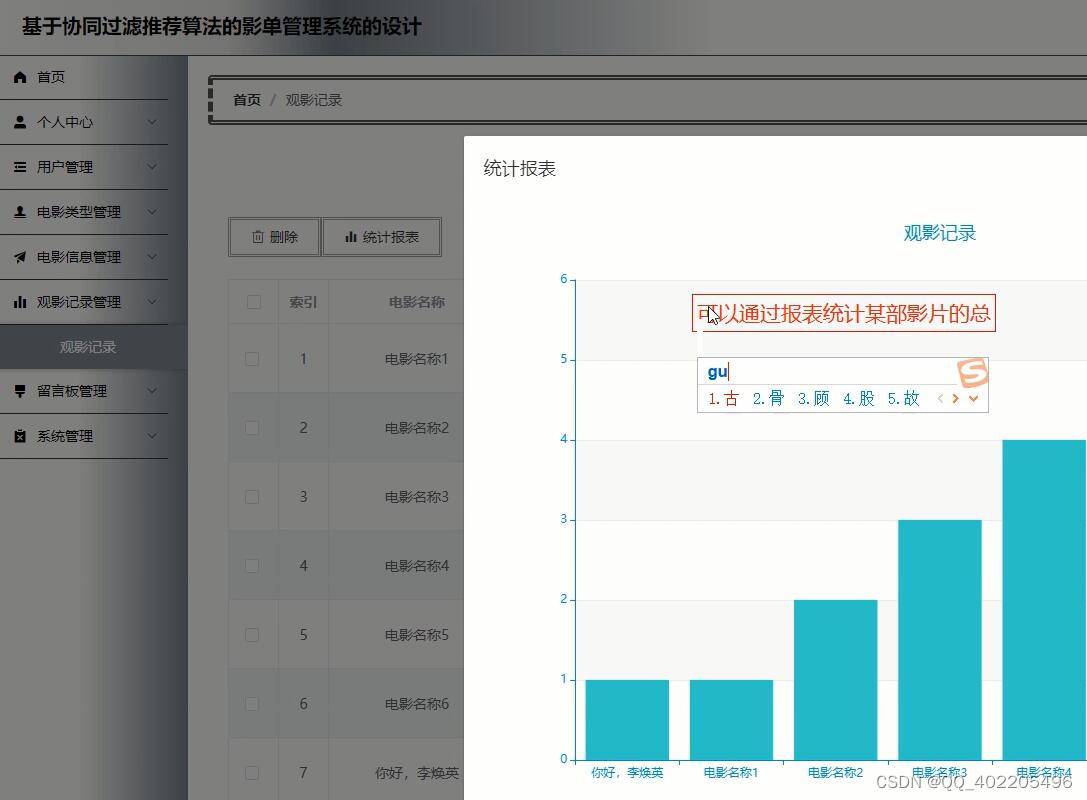
python基于协同过滤推荐算法的电影观后感推荐管理系统的设计
本课题所设计的影单管理系统,使用B/S架构,Python语言进行开发,它的优点代码不能从浏览器查看,保密性非常好,比其他的影单管理更具安全性。Python还容易修改和调试,毕竟影视是在不断发展过程中,难…...

Vue——状态管理库Pinia
写在前面:本文参考小满大牛的pinia专栏 一、Vuex与Pinia Vuex 和 Pinia 均是 Vue.js 的状态管理库,它们为 Vue 应用程序提供了一种集中式的、可预测的状态管理解决方案。 Vuex 是 Vue.js 官方推荐的状态管理库之一。它的核心概念包括 state、mutation…...
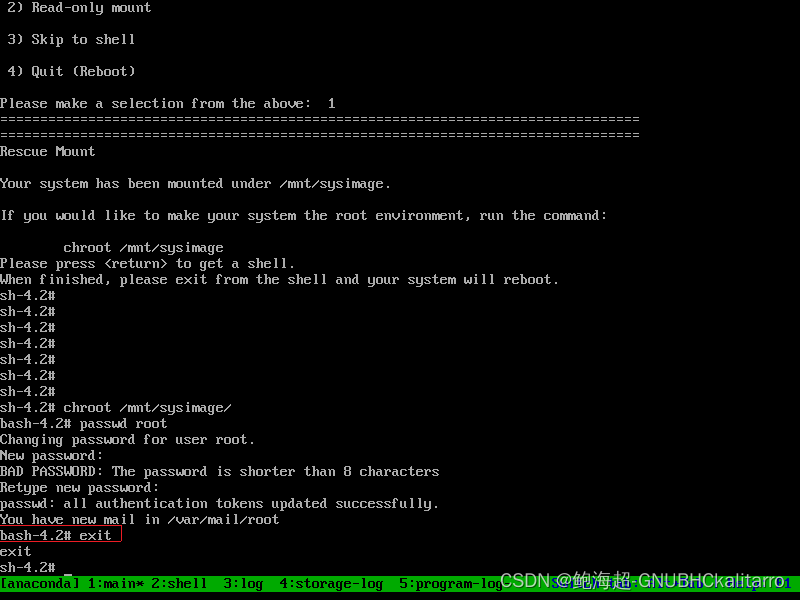
Linux:忘记root密码解决办法
如果你是虚拟机只要将光盘镜像连接到虚拟机上,以光盘iso镜像启动 如果你是真机或服务器那将实体u盘或实体光盘连接至设备并且以连接的设备启动 开机时候打断开机 使用 (u盘|光盘)引导启动 troubleshooting rescue a centos system 输入 1…...
 - RUN 指令详解)
Dockerfile(4) - RUN 指令详解
RUN 运行命令 shell 形式 命令在 shell 中运行Linux 上默认为 /bin/sh -cWindows 上 cmd /S /C RUN <command> exec 形式 RUN ["executable", "param1", "param2"] 必须双引号,不能是单引号 两种写法的实际栗子 RUN …...
一个完整的APP定制开发流程是怎样的?
随着移动互联网的发展,越来越多的 APP应用软件进入人们的生活,让我们的生活更便捷、更舒适。而随着互联网技术的进步,移动互联网应用软件开发行业也越来越成熟,为了适应市场需求,各种功能强大、性能良好的 APP应用软件…...

【数据结构】24王道考研笔记——线性表
线性表 目录 线性表定义和基本操作顺序表静态顺序表动态顺序表 链表单链表不带头结点:带头结点: 双链表循环链表循环单链表:循环双链表: 静态链表 顺序表链表比较逻辑结构:存储结构:基本操作: 定…...

【Linux C】基于树莓派/香橙派的蓝牙服务端——支持多蓝牙设备接入
一、需求 在树莓派/香橙派上利用开发板自带的蓝牙作为一个蓝牙服务端(主机),允许外来设备(从机)通过蓝牙接入进行通信,通信格式为透传方式;采用的编程语言为Linux C 二、环境准备 bluez安装 …...

鸿蒙App开发选择Java还是JavaScript?
众所周知, Java和 JavaScript是两种编程语言,这两种语言在不同的环境中都有许多用途。在鸿蒙 App开发中, Java和 JavaScript是两种常见的编程语言,它们都具有广泛的应用,并且都有其独特的优势。下面我们将就这两种编程…...

【Android】CountDownTimer的使用
android中怎么实现倒计时 在Android中,可以使用CountDownTimer类来实现倒计时。以下是一个简单的示例: javaCopy new CountDownTimer(30000, 1000) {public void onTick(long millisUntilFinished) {// 每次倒计时间隔1秒,更新UI上的倒计时剩…...
】:: ls :: 查看指定目录下的内容)
Linux :: 【基础指令篇 :: 文件及目录操作:(1)】:: ls :: 查看指定目录下的内容
前言:本篇是 Linux 基本操作篇章的内容! 笔者使用的环境是基于腾讯云服务器:CentOS 7.6 64bit。 学习集: C 入门到入土!!!学习合集Linux 从命令到网络再到内核!学习合集 目录索引&am…...

【商品详情 +关键词搜索】API 接口系列
首先,大家要到官方主页去申请一个 appkey,这个是做什么用的呢?App Key 是应用的唯一标识,TOP 通过 App Key 来鉴别应用的身份。AppSecret 是 TOP 给应用分配的密钥,开发者需要妥善保存这个密钥,这个密钥用来…...

RabbitMQ学习-发布确认高级
发布确认springboot版本 确认机制方案: 代码架构图: 配置文件: 在application.properties全局配置文件中添加spring.rabbitmq.publish-confirm-type属性,这个属性有以下几种值 none:禁用发布确认模式(默认)0 correlated:发布消…...

重载和内联函数
函数的默认参数 默认参数是指调用函数的时候,如果不写实参,那么将使用一个缺省值。 使用默认参数可以使你的函数更加灵活,同时减少了在不同上下文中为相同的参数重复编写相同的代码的需要。 return_type function_name(data_type paramete…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
