回归测试最小化(贪心算法,帕累托支配)
回归测试最小化(贪心算法,帕累托支配)
介绍
有时我们不能只是重新运行我们的测试(例如,当我们
换界面)。
回归测试可能很昂贵:
(1)一些公司通宵运行回归测试套件。
(2) 对于嵌入式系统,我们可能必须测试正在使用的软件,例如 汽车或飞机, 这可能需要几个月的时间。
(3) 自动驾驶汽车的回归测试? 模拟测试有帮助,但不是完整的解决方案。
有兴趣找到选择回归测试套件子集的好方法。
类似的问题出现在持续集成中。
我们可能会选择只运行一些测试用例:
我们最小化测试套件。通常基于标准
我们可以对测试用例进行排序(优先排序):
目的是,如果发生故障,则很可能在早期发生测试。允许开发人员更早地解决故障
测试套件最小化中的问题
(1) 我们假设我们已经得到了一个测试套件 T。
(2) 我们要找到满足某些性质(例如覆盖率)的T 的最小子集T0。
(3) 理想情况下,保证 T0 与 T 一样有效。
(4) 大多数方法提供较弱的保证
删除冗余测试用例
(1) 当我们根据系统的变化进行回归测试时,可以使用这个概念。
(2) 要求我们已经记录了每个测试用例执行了什么代码:
这些信息可以在测试用例被收集时收集
以前用过。
(3) 我们只使用执行更改(或删除)代码的测试用例。
(4) 其他测试用例应该是多余的(这些测试用例的行为应该没有变化)
测试套件最小化的一般方法
(1) 其他方法旨在保护某些属性。
(2) 大部分重点都放在代码覆盖率上(例如分支覆盖率)。
(3) 那么问题是:
找到回归测试套件 T 的最小子集 T0,使得 T0 和 T 具有相同的覆盖率。
(4) 希望保持覆盖范围可以使我们保持有效性。
注意:如果测试执行的成本不同,那么我们可能想要一个最便宜(执行)的测试套件,而不是最小的测试套件。
正式化覆盖范围的使用
假设我们有覆盖项 C = {c1,…,ck}(例如分支),测试站点 T = {t1,…,tn} 覆盖了所有这些,并且每个 ti 属于 T 覆盖了给定的覆盖项集 Cti .
优化问题是:找到 T 的最小子集 T0,使得:
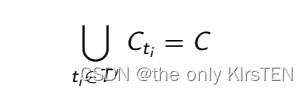
这对应于NP-complete Set Cover problem。
Set Cover 问题是计算机科学和数学中的经典计算问题。 它属于一类称为 NP-complete 问题的问题,NP-complete 问题是一组尚未找到可以在多项式时间内解决所有实例的有效算法的问题。
集合覆盖问题可以定义如下:给定一个由 n 个元素组成的宇宙集合 U 和 U 的子集 S1, S2, …, Sk 的集合,从 S 中找到并集覆盖所有元素的子集的最小数量 在美国
换句话说,我们试图从 S 中找到子集的最小可能子集,使得它们的并集包含 U 中的所有元素。S 中的每个子集可能覆盖一组不同的元素。
已知集合覆盖问题是 NP 完全问题,这意味着它不太可能有多项式时间算法来解决问题的所有实例。 这意味着随着问题规模的增加,找到最佳解决方案所需的时间呈指数增长。
精确解决方案
优化问题是 NP 完全问题。
测试套件通常很大(否则我们不需要最小化它们!)。
所以:我们的问题实例通常很大。
通常无法准确解决问题:我们只能依靠启发式方法。
一个简单的贪心算法
从空集开始。
添加一个涵盖大多数项目的测试用例 t 并从中尚未使用的集合删除 t
在每次迭代中,添加一个剩余的具有最高的覆盖率的测试用例。
当测试套件提供完全覆盖时终止。
一个简单的贪心算法并不总是一个好的方法。

更好的贪心算法
以前的贪心算法的问题在于它确实不考虑已经达到的覆盖率。
我们可以对此进行如下改进(称为 Additional Greedy
在文献中):
从空集开始并添加其中一个测试用例涵盖大部分项目。 在每次迭代中,添加一个覆盖大多数当前未发现项目的测试用例。当测试套件提供完全覆盖时终止。
已知这种贪心算法对集合覆盖问题有效(它们提供了一个很好的近似值)

贪心算法的目标是在每一步选择覆盖最大数量未覆盖元素的子集。为了获得更好的覆盖率,改进的附加贪心算法可以从子集 A 或子集 E 开始。假设它从子集 A 开始。然后,我们选择子集 C,它涵盖元素 4。接下来,我们选择子集 D,它涵盖元素 5. 子集 C 和子集 D 各有一个额外的覆盖项目,而其他子集没有。
因此,示例顺序 A、C、D 提供了更好的覆盖率,因为它在覆盖所有元素的同时选择了更少的子集。 它减少了冗余并优化了贪婪算法实现的覆盖范围。
备择方案
还有一些工作使用元启发式算法来解决优化问题。
经常使用遗传算法的形式(但也考虑过其他类型)。
多目标方法
我们可以将问题概括为:
找到一个回归测试套件 T0,使得没有更小的测试套件提供与 T0 相同的覆盖率。
这里我们正在优化两个目标函数:
最大化覆盖范围和最小化成本
我们可以包括额外的措施,例如不同形式的覆盖,使其比贪心算法更灵活。
多目标优化算法返回一组取舍。
遗传算法 (GA) 是一类受自然选择和遗传学过程启发的优化算法。 它们用于解决复杂的优化和搜索问题。 遗传算法通过维护候选解的种群并应用选择、交叉和变异等遗传算子来创建新一代解来模拟进化过程。
以下是遗传算法通常如何工作的分步概述:
- 初始化:初始化随机候选解的种群(通常称为个体或染色体)。 每个人都代表了问题的潜在解决方案。
- 评价:评价种群中每个个体的适应度。 适应度函数决定解决方案在解决问题时的表现。 它分配一个数值来表示解决方案的质量。
- 选择:根据适应度值从当前种群中选择个体。 具有更高适应性的个体更有可能被选择进行繁殖。
- 交叉:在成对的选定个体之间进行交叉或重组,产生新的后代。 交叉涉及在个体之间交换遗传信息(或构建块)以创建其特征的新组合。
- 突变:对后代的遗传信息进行随机改变或突变。 突变将遗传多样性引入种群,并有助于探索搜索空间的新区域。
- 替换:用新创建的后代替换当前种群中的一些个体。 这确保人口规模保持不变。
- 终止:重复步骤2-6,直到满足终止条件。 此条件可以是最大世代数、达到所需的适应度阈值或时间限制。
- 输出:一旦满足终止条件,算法输出找到的最佳解,通常是适应度值最高的个体。
遗传算法特别适用于解决搜索空间大且复杂的优化问题,以及传统搜索或优化方法可能效率低下的问题。 它们已成功应用于工程设计、调度、数据挖掘和机器学习等各个领域。
比较候选解决方案
比较候选人的经典方法是帕累托支配pareto Dominance。
给定两个候选解决方案 x 和 y,我们有:
如果 x 在所有方面至少与 y 一样好,则 x 帕累托支配 y
目标,并且在至少一个目标上严格优于 y,
这意味着:就优化而言,我们永远不会选择 x。
理想情况下,我们希望找到 Pareto Front:解决方案集
不是由任何其他解决方案支配的帕累托。
有许多元启发式算法:
最著名的可能是非支配排序遗传算法 II (NSGA-II); 现在有 NSGA-III
为了说明帕累托支配,让我们考虑一个具有两个目标的示例:最大化利润和最小化成本。 我们有两个解决方案,解决方案 A 和解决方案 B,具有以下目标值:
解决方案 A:利润 = 100 美元,成本 = 50 美元
解决方案 B:利润 = 120 美元,成本 = 60 美元
为了确定支配关系,我们比较了基于两个目标的解决方案。 在这种情况下,与解决方案 B 相比,解决方案 A 的利润较低,但成本也较低。因此,解决方案 A 不会被解决方案 B 所支配,因为它在成本方面更好。 另一方面,与解决方案 A 相比,解决方案 B 具有更高的利润和更高的成本。这意味着解决方案 B 在利润方面优于解决方案 A。
因此,解决方案 A 和解决方案 B 都不会相互支配。 它们都是帕累托最优的,因为在不牺牲另一个目标的性能的情况下,两种解决方案都不能在一个目标上得到改进。 这是帕累托前沿的示例,它表示多目标优化问题中所有非支配解的集合。
相关文章:

回归测试最小化(贪心算法,帕累托支配)
回归测试最小化(贪心算法,帕累托支配) 介绍 有时我们不能只是重新运行我们的测试(例如,当我们 换界面)。 回归测试可能很昂贵: (1)一些公司通宵运行回归测试套件。 (2) 对于嵌入式系统,我们可能必须测试正在使用的软件࿰…...

Python系列模块之标准库shutil详解
感谢点赞和关注 ,每天进步一点点!加油! 目录 一、shutil介绍 二 、使用详解 2.1 复制函数 2.1.1 shutil.copy 2.1.2 shutil.copy2 2.1.3 shutil.copyfile 2.1.4 shutil.copytree 2.2 移动文件 2.2.1 shutil.move 2.3 删除文件 2.3…...

pb如何播放Flash
---- Flash动画不仅包含动画,还可有声音、超文本连接,同时由于它是矢量格式文件,生成的这种包含动画、声音等的文件(*.swf)很小,非常适 合在网络上传输使用,因而在当前Web网页技术中得到很快发展。本文讨论在PowerBuilder6.5数据库编程中用Flash4提供的控件"Swflas…...
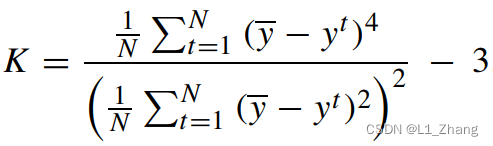
独立成分分析ICA
独立成分分析 ICA 1. 算法原理简介2.源信号与混合信号的差异2.1 独立性 Independence2.2 高斯性 Normality2.3 复杂性 Complexity 3.非高斯性的度量3.1 峭度 Kurtosis 参考文献 blind source separation (BSS) 1. 算法原理简介 mixing得到signal mixture过程: x 1…...

从零开始之如何在React Native中使用导航
好的,让我们开始学习如何在React Native中使用导航。 安装React Navigation 首先,你需要安装React Navigation库。在项目文件夹中打开终端窗口,并运行以下命令: npm install react-navigation/native 或者 yarn add react-nav…...
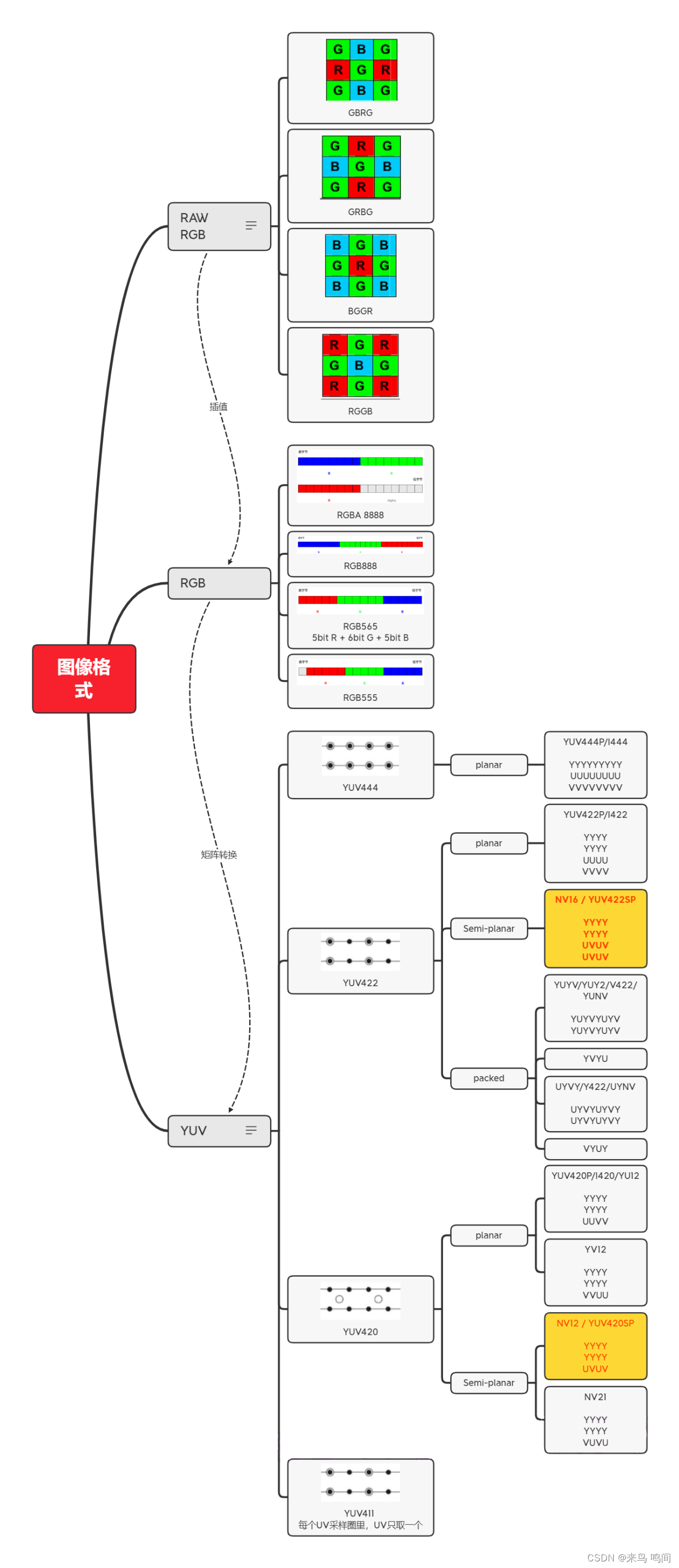
RAW、RGB 、YUV三种图像格式理解
文章目录 1. 背景2. 相关概念2.1 颜色与色彩空间2.2 RAW图像2.3 RGB图像2.4 YUV图像 3. 分类简图 RAW、RGB 、YUV三种图像格式理解 1. 背景 在工作中,经常听到用来描述图像格式的RAW,RGB与YUV,但一直没有系统的进行了解,处于局部认…...

关于对【mysql存储过程】的理解与简述
【版权声明】未经博主同意,谢绝转载!(请尊重原创,博主保留追究权) https://blog.csdn.net/m0_69908381/article/details/130857854 出自【进步*于辰的博客】 【存储过程】这个知识点,我在大二下期学习【mys…...

贪吃蛇游戏的制作记录
关于蛇的实现代码 #include "snake.h" #include "globalvar.h" #include <graphics.h> int fangXiang 1;//方向 0 右 1 上 2 左 3 下 int snakeHang[100] { 10,11,12,13,14 };//蛇 每节所在行 int snakeLie[100] { 10,10,10,10,10 };//蛇 每节所…...

Go基础入门
Go是一种现代的、高效的、开源的编程语言,由Google开发。它的语法简洁、易于学习和使用,支持并发编程,特别适合构建网络应用和分布式系统。本篇文章将介绍Go语言的基础语法和常用特性,帮助初学者快速入门。 一、Go语言的基础语法…...

JavaScript教程(二)
BOM浏览器对象模型 什么是BOM BOM(Browser Object Model)即浏览器对象模型,它提供了独立于内容而与浏览器窗口进行交互的对象,其核心对象是 window;BOM由一系列相关的对象构成,并且每个对象都提供了很多方…...

设计模式之代理模式
代理模式的定义是:为其他对象提供一种代理以控制对这个对象的访问。 因为代理类与服务类实现同样的接口,所以代理类能代替服务类提供给客户端。当客户端使用代理类时,代理类能对请求进行处理(例如增加访问控制、缓存请求结果、隐…...
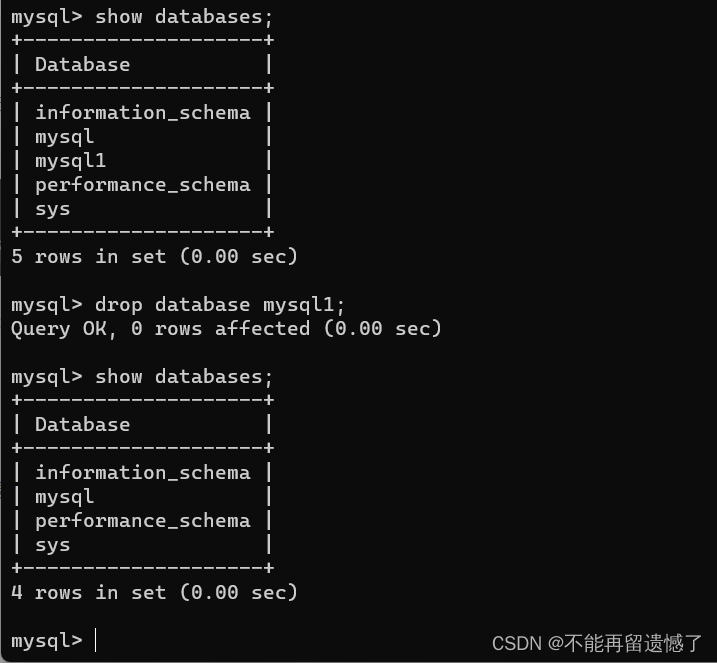
初识MySQL
💕与其抱怨生活的不公,不如积极行动改变它。💕 🐼作者:不能再留遗憾了🐼 🎆专栏:MySQL学习🎆 🚗本文章主要内容:简单了解什么是MySQL、MySQL的发展…...
之ADCS证书服务攻击)
内网渗透(八十五)之ADCS证书服务攻击
ADCS证书服务攻击 漏洞背景 2021年6月17日,国外安全研究员 Will Schroeder 和 Lee Christensen 共同发布了针对ADCS(Active Directory Certificate Service, 活动目录证书服务)的攻击手法。同年8月5日,在Black Hat 2021上 Will Schroeder 和 Lee CHristensen 对该攻击手法进…...
通过python封装1688图片搜索商品数据接口,拍立淘API接口
1688图片搜索API封装接口是一个可以帮助用户快速使用1688图片搜索API的接口封装库。该接口封装库可以帮助用户快速引入1688图片搜索API,并提供各种参数配置和封装的API调用方法,以方便用户快速实现自己的图片搜索需求。 该接口封装库将1688图片搜索API的…...
)
HashMap的源码分析(基于JDK1.8)
HashMap的源码分析(基于JDK1.8) Java中的HashMap是一种常用的数据结构,它是基于哈希表的数据结构,可以用来存储键值对。在HashMap中,每个键值对被称作一个Entry,每个Entry包含一个键和一个值。HashMap的实…...
)
算法能力-数据安全复合治理框架和模型解读(5)
数据治理,数据安全治理行业在发展,在实践,所以很多东西是实践出来的,哪有什么神仙理论指导,即使有也是一家之说,但为了提高企业投产比,必要的认知是必须的,落地数据安全治理科技水平差异直接决定产品和项目是否可持续性,当前和未来更需要专业和有效创新。数据安全治理…...

java从入门到起飞——基础概念
目录 背景注释和关键字注释关键字 常量变量数据类型计算存储单元数据类型分类 标识符小驼峰命名法(方法、变量)大驼峰命名法(类) 类型转换自动类型转换强制类型转换 计算机中的数据存储总结 背景 学编程这么长时间了,重…...

C语言判断队列满or空
1 静态数组队列 循环队列通常使用数组来实现,判别循环队列是否满或空,可以借助两个变量front和rear。 判空:当front和rear相等时,队列为空。 判满:当(front 1) % n rear时,队列为满,其中n为…...
好考吗?)
系统中级集成项目管理工程师(中项)好考吗?
软考系统集成项目管理工程师是一项非常重要的考试,对于从事信息技术和管理方面的人员来说,这是一个非常有用的证书。 对于零基础的考生来说,软考系统集成项目管理工程师是否好考,主要取决于他们的学习态度和学习方法。 一般而言…...

【Java多线程进阶】CAS机制
前言 CAS指的是Compare-And-Swap(比较与交换),它是一种多线程同步的技术,常用于实现无锁算法,从而提高多线程程序的性能和扩展性。本篇文章具体讲解如何使用 CAS 的机制以及 CAS 机制带来的问题。 目录 1. 什么是CAS&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
