LLM之高性能向量检索库
LLM向量数据库
- 高性能向量检索库
- milvus
- 简介
- 安装
- 调用
- faiss
- 简介
- 安装
- 调用
高性能向量检索库
milvus
简介
Milvus 是一个开源的向量数据库引擎,旨在提供高效的向量存储、检索和分析能力。它被设计用于处理大规模的高维向量数据,常用于机器学习、计算机视觉、自然语言处理和推荐系统等领域。
Milvus 提供了多种功能和特性,使其成为处理向量数据的理想选择。以下是一些 Milvus 的主要特点:
- 高性能:Milvus 使用了高度优化的数据结构和索引算法,以实现快速的向量检索。它支持多种索引类型,如平面索引、倒排索引和 HNSW(Hierarchical Navigable Small World)等,这些索引能够加速向量的相似度搜索。
- 可扩展性:Milvus 具备良好的可扩展性,可以轻松地扩展到大规模的向量数据集。它支持分布式部署,可以在多个节点上进行数据存储和查询操作,实现高吞吐量和低延迟。
- 多样化的向量类型:Milvus 支持多种向量类型,包括浮点型向量、二进制向量和文本向量等。这使得它可以适应不同领域和应用中的向量数据需求。
- 多语言支持:Milvus 提供了多种编程语言的 SDK(软件开发工具包),包括 Python、Java、Go 和 C++ 等,使开发者可以方便地集成 Milvus 到他们的应用程序中。
- 可视化管理界面:Milvus 提供了一个易于使用的 Web 界面,用于管理和监控向量数据库。开发者可以通过该界面进行数据导入、索引构建和查询优化等操作,同时还能够查看系统状态和性能指标。
总之,Milvus 是一个功能强大的向量数据库引擎,通过其高性能、可扩展性和多样化的特性,能够有效地存储和检索大规模的高维向量数据。它在许多领域的应用中发挥着重要作用,帮助开发者加速向量相关任务的开发和部署。
安装
-
docker 安装镜像:docker pull milvusdb/milvus:cpu-latest
-
创建工作目录:
mkdir milvus
cd milvus
mkdir congf
mkdir db
mkdir logs
mkdir wal
我的目录结构是:
milvus│├─conf //配置文件目录│ server_config.yaml //配置文件 搜索引擎配置都在这里修改│├─db //数据库存储目录 你的索引与向量存储的位置│└─logs //日志存储目录 │└─wal // 预写式日志相关配置
server_config.yaml
docker run -it milvusdb/milvus:cpu-latest bash
docker cp 74c20a680091:/var/lib/milvus/conf/server_config.yaml milvus/conf/
-
启动容器
docker run -td --name mymilvus -e "TZ=Asia/Shanghai" -p 19530:19530 -p 19121:19121 -v /work/lnn_workspace/chatgpt/search/milvus/conf:/var/lib/milvus/conf -v /work/lnn_workspace/chatgpt/search/milvus/db:/var/lib/milvus/db -v /work/lnn_workspace/chatgpt/search/milvus/logs:/var/lib/milvus/logs milvusdb/milvus:cpu-latestdocker ps | grep mymilvus
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-orhH8dlK-1685346967888)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20230519105321396.png)]
- 安装pymilvus
pip install pymilvus==1.1.2
ps:注意这里安装最新版本可以会无法正常调用,1.1.2经过测试可正常使用
调用
# -*- coding: utf-8 -*- # 导入相应的包
import numpy as np
from milvus import Milvus, MetricType # 初始化一个Milvus类,以后所有的操作都是通过milvus来的
milvus = Milvus(host='localhost', port='19530') # 向量个数
num_vec = 5000
# 向量维度
vec_dim = 768
# name
collection_name = "test_collection"
# 创建collection,可理解为mongo的collection
collection_param = { 'collection_name': collection_name, 'dimension': vec_dim, 'index_file_size': 32, 'metric_type': MetricType.IP # 使用内积作为度量值
}
milvus.create_collection(collection_param) # 随机生成一批向量数据
# 支持ndarray,也支持list
vectors_array = np.random.rand(num_vec, vec_dim) # 把向量添加到刚才建立的collection中
status, ids = milvus.insert(collection_name=collection_name, records=vectors_array) # 返回 状态和这一组向量的ID
milvus.flush([collection_name]) # 输出统计信息
print(milvus.get_collection_stats(collection_name)) # 创建查询向量
query_vec_array = np.random.rand(1, vec_dim)
# 进行查询,
status, results = milvus.search(collection_name=collection_name, query_records=query_vec_array, top_k=5)
print(status)
print(results) # 如果不用可以删掉
status = milvus.drop_collection(collection_name) # 断开、关闭连接
milvus.close()
collection_name = "test_collection"
- 定义集合名称为test_collection
collection_param = {'collection_name': collection_name,'dimension': vec_dim,'index_file_size': 32,'metric_type': MetricType.IP
}
milvus.create_collection(collection_param) - collection_name 指定集合名称为test_collection
- dimension 表示集合中向量的维度,由vec_dim变量赋值
- index_file_size 设置索引文件大小为32MB
- metric_type 设置度量类型为IP,表示使用向量内积作为相似度度量
所以,这段代码定义了集合名称和相关参数,用于在Milvus服务上创建一个新的集合。
在Milvus中,集合相当于关系数据库的表,是存储向量的基本单元。在创建集合时,我们需要指定:
1. 集合名称:唯一标识一个集合
2. 向量维度:集合中向量的特征数量
3. 度量类型:测量向量之间相似度的算法,如IP(内积)、L2(欧氏距离)等
4. 索引文件大小:用于提高搜索性能,索引文件会存储向量的索引信息
faiss
简介
Faiss是Facebook开源的一个向量检索库,用于大规模向量集合的索引和搜索。主要功能包括:
- 支持多种索引结构: IVF, IVFFlat, HNSW, etc。这些索引结构可以实现高精度和高召回的向量搜索。
- 支持多种度量方式:内积,欧氏距离,cosine 相似度等。可选择合适的度量方式对向量集合建立索引。
- 快速的索引构建与搜索:Faiss使用GPU加速,可以实现亿量级向量的索引构建和搜索。
- 降维与聚类:Faiss提供PCA,IVFFlat等算法进行向量降维,并支持Kmeans算法进行向量聚类。
- 高级特性:Faiss支持在线学习,异构向量检索,索引压缩等高级特性。
Faiss的典型应用有:
图像检索:在大规模图片数据库中找到与输入图片最相似的图片。
文本匹配:快速找到与输入文本最相近的文本内容。
推荐系统:根据用户兴趣对大量商品进行快速检索和推荐。
声纹识别:在海量语音数据中实现语音识别和检索。
Faiss提供C++, Python和Java语言接口,可以轻松构建向量检索系统。如果需要管理和搜索海量高维向量,Faiss是一个非常好的选择。
安装
install faiss-cpu
调用
# 导入库
import numpy as np
import faiss # 向量个数
num_vec = 5000
# 向量维度
vec_dim = 768
# 搜索topk
topk = 10 # 随机生成一批向量数据
vectors = np.random.rand(num_vec, vec_dim) # 创建索引
faiss_index = faiss.IndexFlatL2(vec_dim) # 使用欧式距离作为度量
# 添加数据
faiss_index.add(vectors) # 查询向量 假设有5个
query_vectors = np.random.rand(5, vec_dim)
# 搜索结果
# 分别是 每条记录对应topk的距离和索引
# ndarray类型 。shape:len(query_vectors)*topk
res_distance, res_index = faiss_index.search(query_vectors, topk)
print(res_index)
print(res_distance)
相关文章:

LLM之高性能向量检索库
LLM向量数据库 高性能向量检索库milvus简介安装调用 faiss简介安装调用 高性能向量检索库 milvus 简介 Milvus 是一个开源的向量数据库引擎,旨在提供高效的向量存储、检索和分析能力。它被设计用于处理大规模的高维向量数据,常用于机器学习、计算机视觉…...

实体类注解
目录 一、TableField注解 二、TableId注解 三、Table注解 四、TableLogic注解 五、Getter与Setter注解 六、EqualsAndHashCode注解 七、Accessors注解 一、TableField注解 Data NoArgsConstructor //空参构造方法 AllArgsConstructor //全参构造方法 TableName("t…...

常见数据结构种类
常见数据结构种类 数据存储的常用结构有:栈、队列、数组、链表和红黑树 a.队列(queue) – 先进先出,后进后出。 – 场景:各种排队。叫号系统。 – 有很多集合可以实现队列。 b.栈(stack) – …...
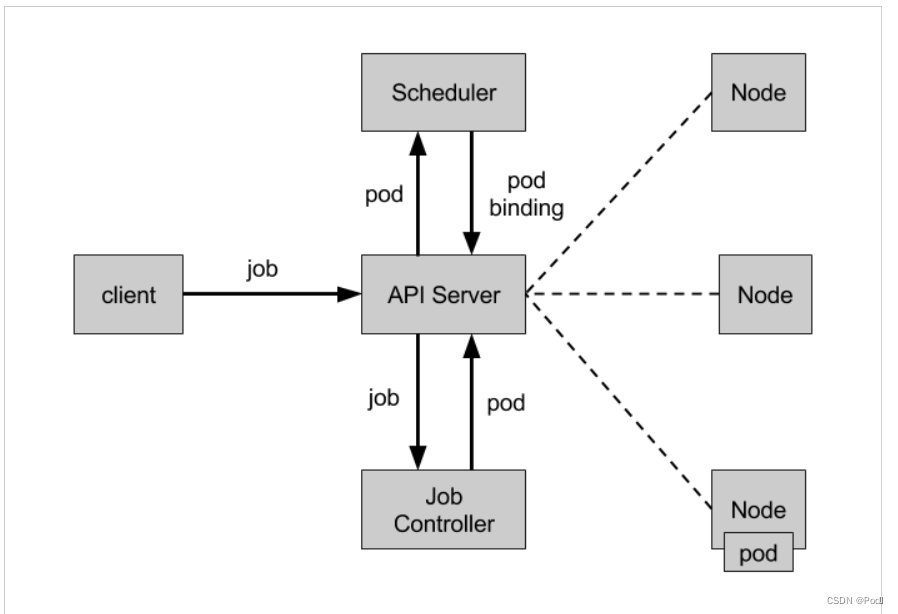
linux高级---k8s中的五种控制器
文章目录 一、k8s的控制器类型二、pod与控制器之间的关系三、状态与无状态化对特点四、Deployment1、Deployment的资源清单文件2、在配置清单中调用deployment控制器3、镜像更新4、金丝雀发布5、删除Deployment 五、Statefulset六、DaemonSet1、daemonset的资源清单文件2、在配…...
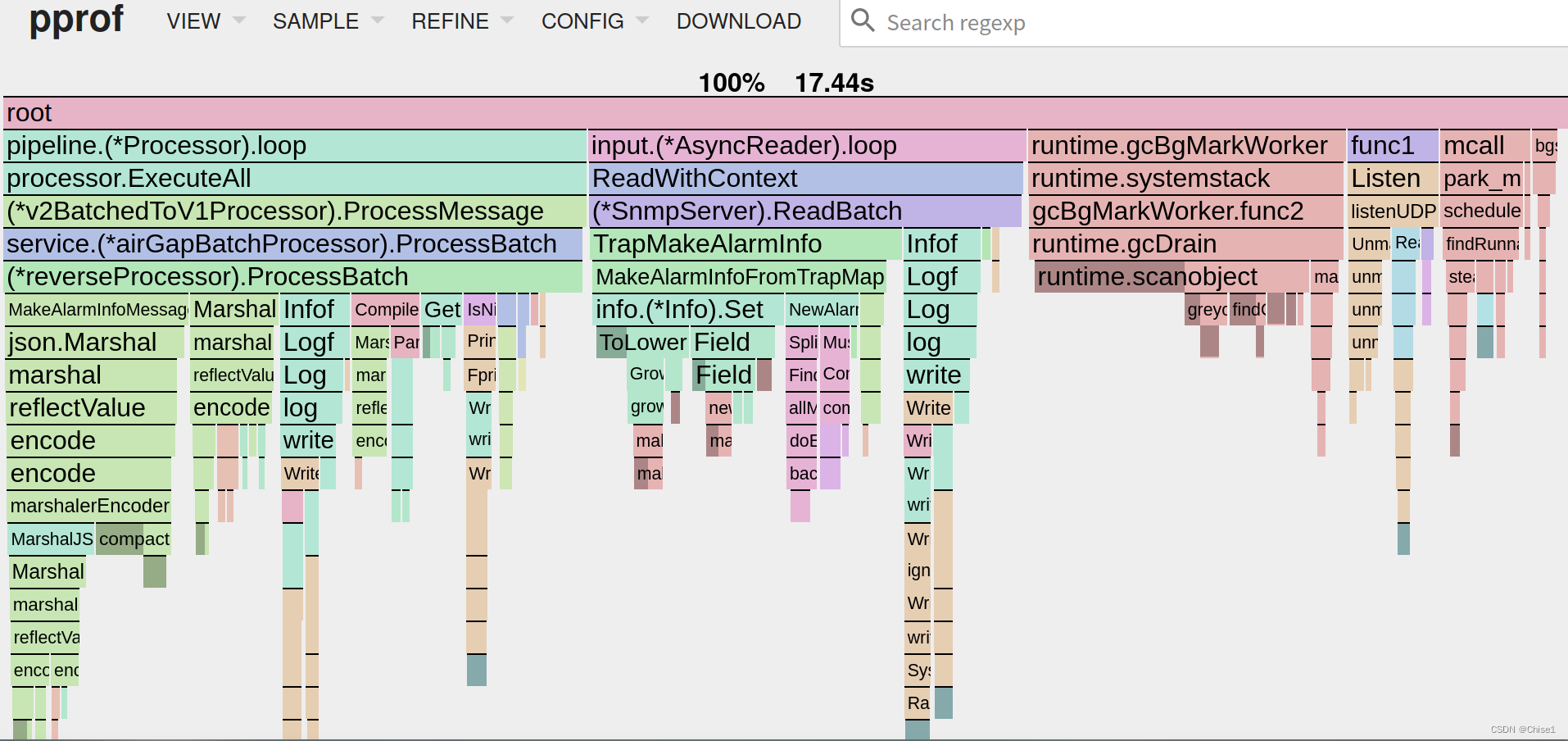
记一次udp服务性能优化经历
目录 概述磁盘io网络io减少重复计算减少内存复制减少互斥锁 概述 手上有个go项目,接收udp信息(主要是syslog和snmp trap)并查询设备信息,将信息结构化(设备ip名称,匹配了什么规则之类的)后发送…...

uniapp和VueI18n多语言H5项目语言国际化功能搭建流程
uniapp多语言项目国家化功能搭建流程 说明:uniapp多语言项目功能搭建分为应用部分和框架部分。 应用部分,即开发者自己的代码里涉及的界面部分的语言翻译。框架部分,即uni-app内置组件和API涉及界面的部分的语言翻译。 功能的搭建是需要un…...
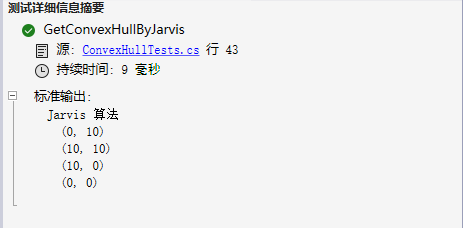
C# | 凸包算法之Jarvis,寻找一组点的边界/轮廓
C#实现凸包算法之Jarvis 文章目录 C#实现凸包算法之Jarvis前言示例代码实现思路测试结果结束语 前言 这篇关于凸包算法的文章,本文使用C#和Jarvis算法来实现凸包算法。 首先消除两个最基本的问题: 什么是凸包呢? 凸包是一个包围一组点的凸多…...
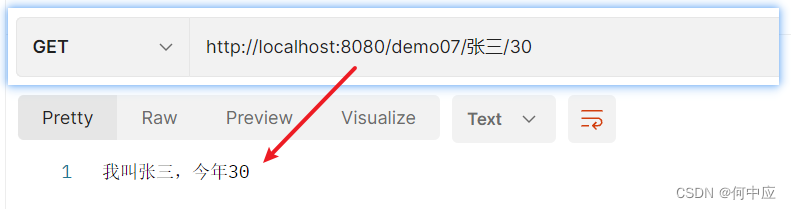
SpringBoot接收请求参数的方式
【方式一】原始方式 因为SpringBoot封装了Servlet,所以也允许使用HttpServletRequest类中的方法来获取 /*** 【方式一】原始方式*/RequestMapping("/demo01")public String demo01(HttpServletRequest request) {// 参数名要与页面提交的参数名一致Strin…...
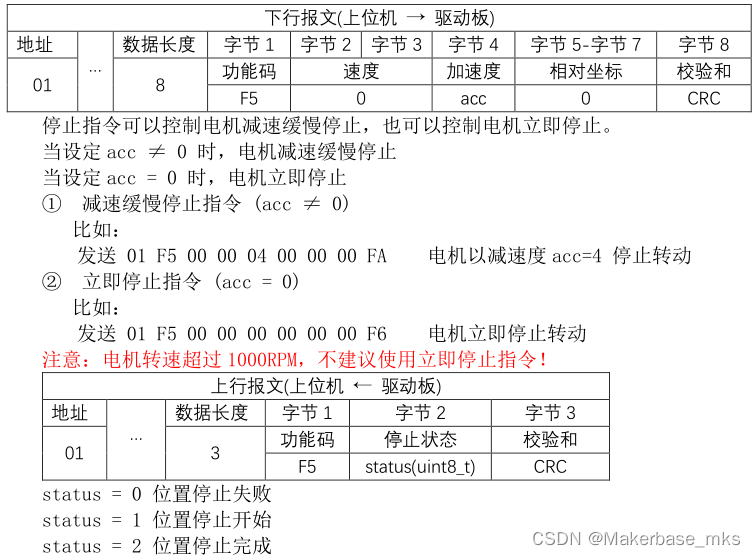
MKS SERVO4257D 闭环步进电机_系列5 CAN指令说明
第1部分 产品介绍 MKS SERVO 28D/35D/42D/57D 系列闭环步进电机是创客基地为满足市场需求而自主研发的一款产品。具备脉冲接口和RS485/CAN串行接口,支持MODBUS-RTU通讯协议,内置高效FOC矢量算法,采用高精度编码器,通过位置反馈&am…...

安捷伦E4440A(Agilent) e4440a 3HZ-26.5G频谱分析仪
Agilent E4440A、Keysight E4440A、HP E4440A频谱分析仪,3 Hz - 26.5 GHz(PSA 系列) Agilent / Keysight PSA 系列 E4440A 高性能频谱分析仪提供强大的一键式测量、多功能功能集和前沿技术,可满足您的项目和需求。选项可供您选…...

华为OD机试真题 Java 实现【最长子字符串的长度】【2022Q4 100分】,附详细解题思路
一、题目描述 给你一个字符串s,字符串s首尾相连组成一个环形,请你在环形中找出‘o’字符出现了偶数次最长子字符串的长度。 二、输入描述 输入一串小写字母组成的字符串。 三、输出描述 输出一个整数。 四、解题思路 题目要求在给定的环形字符串中找出字符’o’出现了…...

【iOS】--对象的底层结构
源码 先转一下源码 //#import <Foundation/Foundation.h> #import <objc/runtime.h>interface LGPerson : NSObject property (nonatomic, strong) NSString *KCName; endimplementation LGPersonendint main(int argc, const char * argv[]) {autoreleasepool {…...

高并发内存池设计_内存池
高并发内存池设计 1. 常用的内存操作函数2. 高性能内存池设计_弊端解决之道弊端一弊端二弊端三弊端四3. 弊端解决之道内存管理维度分析内存管理组件选型4. 高并发内存管理最佳实践内存池技术内存池如何解决弊端?高并发时内存池如何实现?5. 高效内存池设计和实现实现思路 (分而…...

给编程初学者的一封信
提醒:以下内容仅做参考,具体请自行设计。 随着信息技术的快速发展,编程已经成为一个越来越重要的技能。那么,我们该如何入门编程呢?欢迎大家积极讨论 一、自学编程需要注意什么? 要有足够的时间、精力等…...
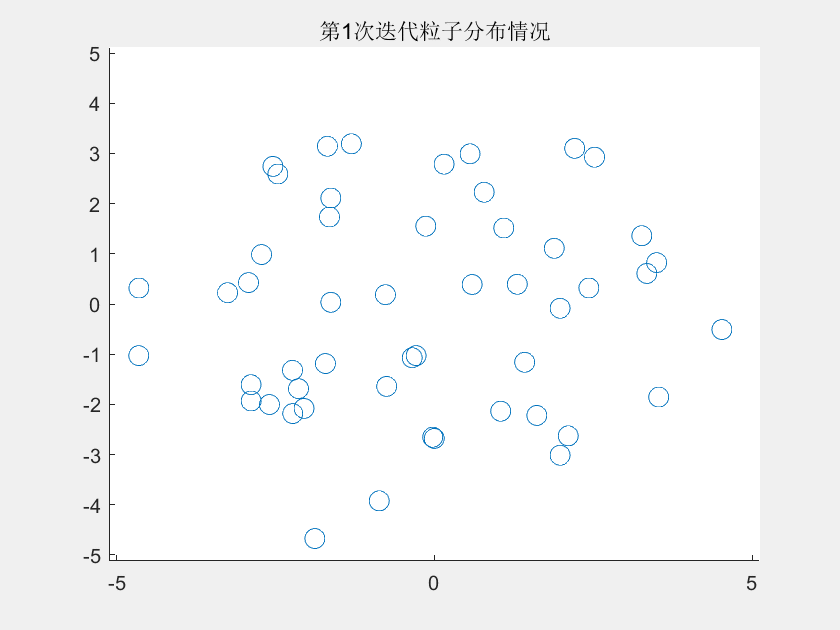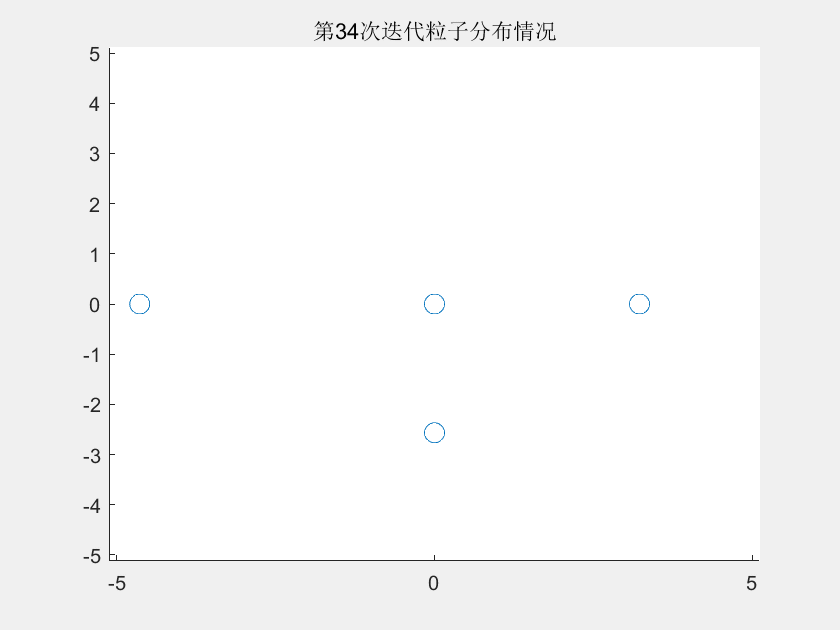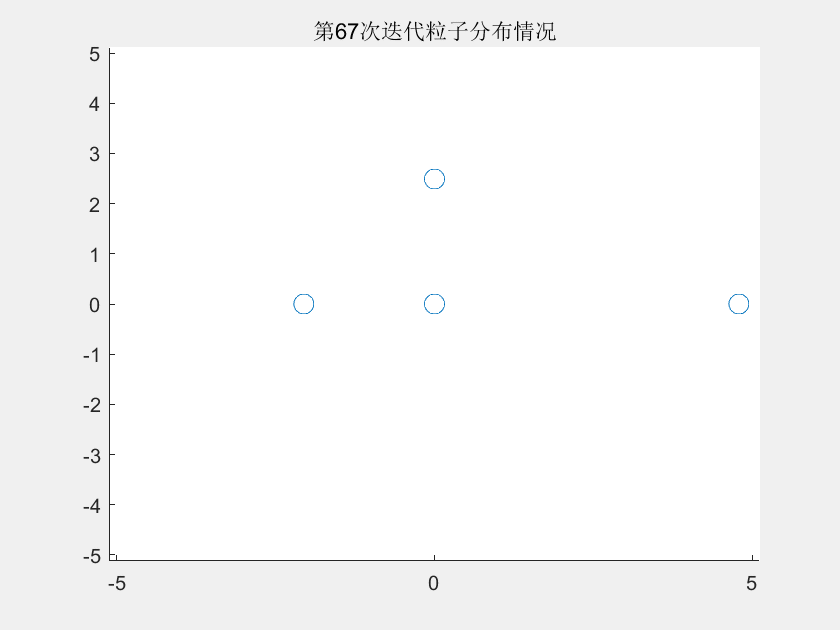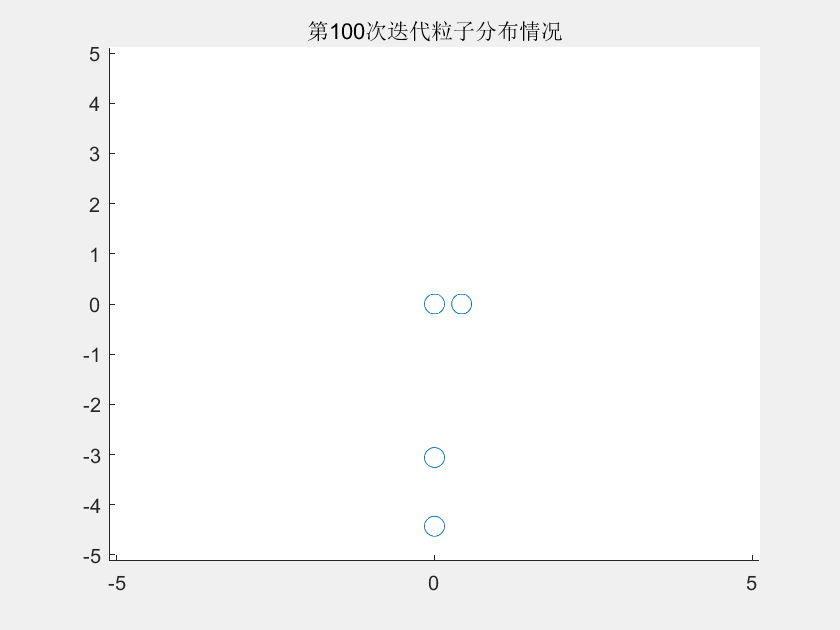
【无功优化】基于改进教与学算法的配电网无功优化【IEEE33节点】(Matlab代码时候)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

数据在内存中的存储(超详细讲解)
目录 浮点数家族 浮点数类型在内存中的存储 一.为什么说整型和浮点数在内存中存储方式不同(证明) 二.浮点数的存储规则 浮点数在计算机内部的表示方法 1.对于M的存储和取出规则 2.对于E的存储和取出时的规则 对前面代码结果进行解释: …...

log4cplus使用示例
1、l4jlog.h封装头文件 #pragma once#include <iostream> #include <log4cplus/logger.h> #include <log4cplus/loggingmacros.h> #include <log4cplus/fileappender.h> #include <log4cplus/layout.h> #include <log4cplus/configurator.h&…...
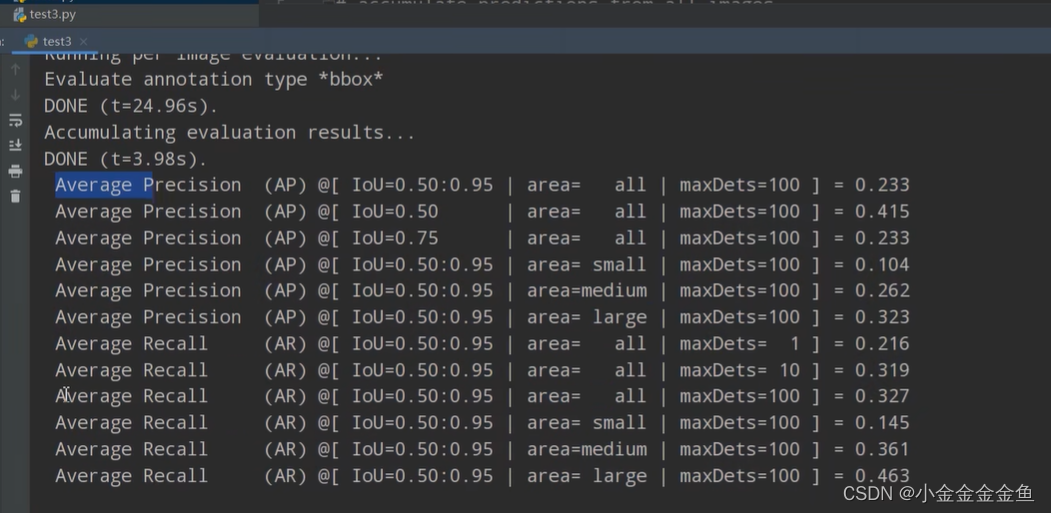
人工智能学习07--pytorch20--目标检测:COCO数据集介绍+pycocotools简单使用
如:天空 coco包含pascal voc 的所有类别,并且对每个类别的标注目标个数也比pascal voc的多。 一般使用coco数据集预训练好的权重来迁移学习。 如果仅仅针对目标检测object80类而言,有些图片并没有标注信息,或者有错误标注信息。…...

learnOpenGL-深度测试
深度测试:OpenGL将一个片段的深度值与深度缓冲的内容进行对比。执行一个深度测试,测试通过则深度缓冲将会更新为新的深度值。测试失败则片段被丢弃。 深度测试片段着色器及模版测试之后执行。 片段着色器中内置变量gl_FragCoord的z值即为深度值。 提前深…...

阿里云服务器数据盘是什么?系统盘和数据盘区别
阿里云服务器系统盘和数据盘有什么区别?系统盘类似Windows电脑的C盘,数据盘相当于其他盘符,数据盘可以有多个而系统盘只能有一个,数据盘可有可无而云服务器系统盘是必须要有的。阿里云服务器网来详细说下阿里云服务器数据盘和系统…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
