数据在内存中的存储(超详细讲解)
目录
浮点数家族
浮点数类型在内存中的存储
一.为什么说整型和浮点数在内存中存储方式不同(证明)
二.浮点数的存储规则
浮点数在计算机内部的表示方法
1.对于M的存储和取出规则
2.对于E的存储和取出时的规则
对前面代码结果进行解释:
代码:
解释如图:
浮点数家族
包括 :float,double,long double
整型家族类型,表示的范围可以在 “limits.h”里查看
浮点数家族表示的范围在 “float.h” 中定义(可以在这里面查浮点数类型表示的精度,最大最小值等...)
以查看浮点数范围为例,打开float.h文件
如:
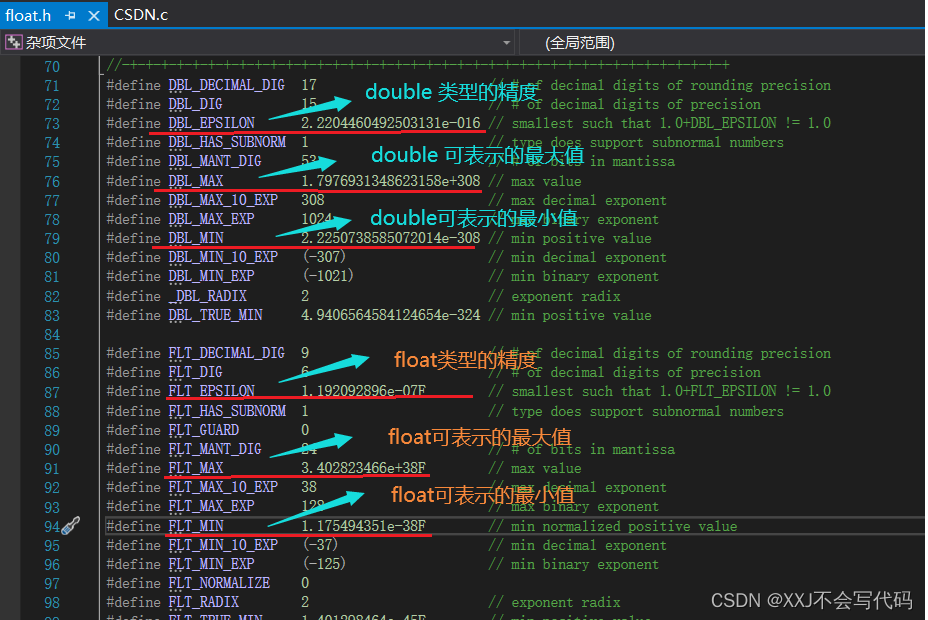
浮点数类型在内存中的存储
一.为什么说整型和浮点数在内存中存储方式不同(证明)
可以通过一个代码来解释整型和浮点数在内存中的存储方式是不同的
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n",*pFloat);return 0;
}运行结果:
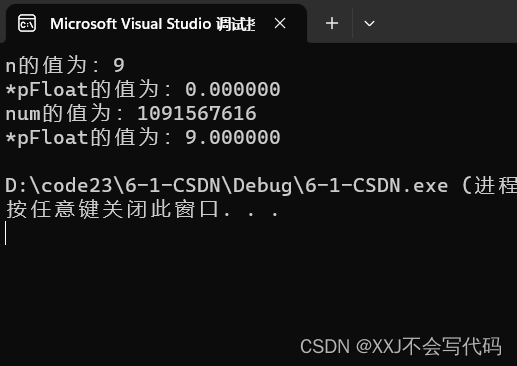
运行结果分析:如果整型类型和浮点数类型的存储的方式一样,
预期结果应该是 9 9.00000 9 9.000000
所以通过这个结果可以看出整型和浮点型在内存中存储的方式有一定的差异
二.浮点数的存储规则
浮点数在计算机内部的表示方法
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式: (-1)^S * M * 2^E (-1)^S 表示符号位,当S=0,V为正数;当S=1,V为负数。 M表示有效数字,大于等于1,小于2。 2^E表示指数位。
举例来说: 十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。 那么,按照上面V的格式,可以得出S=0,M=1.01,E=2;
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。那么,S=1,M=1.01,E=2;
并且IEEE 754规定:
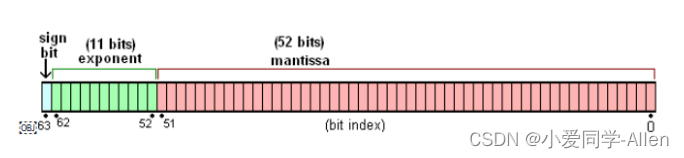
对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。

特别注意的是对M和E的存储还有特别之处
1.对于M的存储和取出规则
首先,M的范围是1<=M<2的数,都可以写成1.xxxxxxx的形式,每个M小数点前面都有1,所以存出的时候只需要把小数点后面的xxxxxxx存储起来,取出的时候再统一在小数点前面加上1;这样的好处是:以32位 浮点数为例,留给M只有23位, 将第一位的1舍去以后,等于可以保存24位有效数字。
2.对于E的存储和取出时的规则
首先,E为一个无符号整数(unsigned int)
因为无符号整数只能表示正数,但是科学计数法中E是可以为负数,所以IEEE 754规定E在存入内存中时加上一个中间值,,对于8位的E,这个中间数 是127;对于11位的E,这个中间 数是1023。
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即 10001001;又如2^-2的E是-2,所以保存成32位浮点数时,必须保存-2+127=125,即01111101,让E变为正数;
指数E从内存中取出还可以再分成三种情况:
1.不全为0和不全为1
E在存储时加了中间值 127 / 1023 ,所以E在取出时用减去 127 / 1023 ,得到真实值
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其阶码为-1+127=126,表示为 01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进 制表示形式为:0 01111110 00000000000000000000000
2.E全为0时
浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于 0的很小的数字(即为什么下图结果为0.00000)

3.E全为1
即2^E,例:E为8位时,11111111转换为十进制为255,即2^255,是个很大的数了,更不用说11位的E了;所以,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
对前面代码结果进行解释:
代码:
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}解释如图:

相关文章:

数据在内存中的存储(超详细讲解)
目录 浮点数家族 浮点数类型在内存中的存储 一.为什么说整型和浮点数在内存中存储方式不同(证明) 二.浮点数的存储规则 浮点数在计算机内部的表示方法 1.对于M的存储和取出规则 2.对于E的存储和取出时的规则 对前面代码结果进行解释: …...

log4cplus使用示例
1、l4jlog.h封装头文件 #pragma once#include <iostream> #include <log4cplus/logger.h> #include <log4cplus/loggingmacros.h> #include <log4cplus/fileappender.h> #include <log4cplus/layout.h> #include <log4cplus/configurator.h&…...
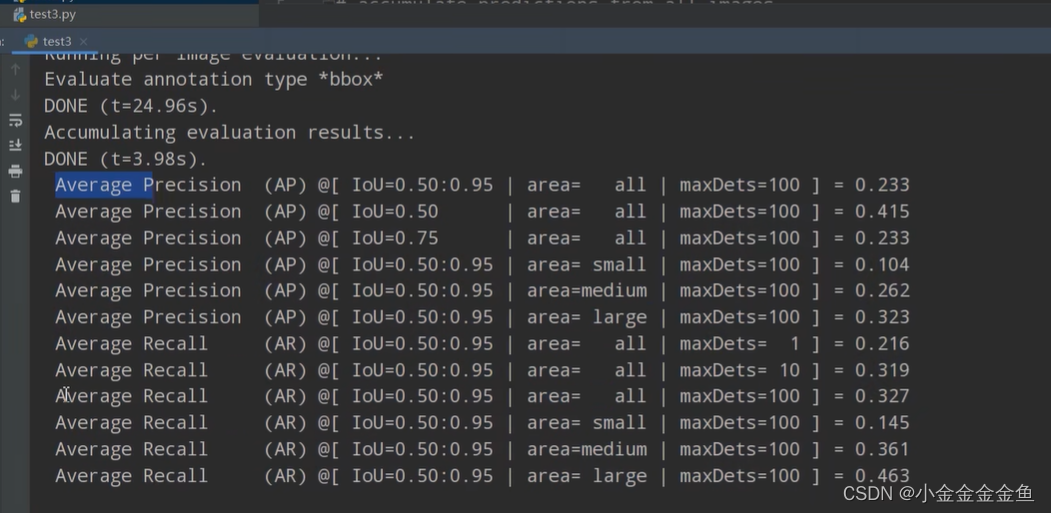
人工智能学习07--pytorch20--目标检测:COCO数据集介绍+pycocotools简单使用
如:天空 coco包含pascal voc 的所有类别,并且对每个类别的标注目标个数也比pascal voc的多。 一般使用coco数据集预训练好的权重来迁移学习。 如果仅仅针对目标检测object80类而言,有些图片并没有标注信息,或者有错误标注信息。…...

learnOpenGL-深度测试
深度测试:OpenGL将一个片段的深度值与深度缓冲的内容进行对比。执行一个深度测试,测试通过则深度缓冲将会更新为新的深度值。测试失败则片段被丢弃。 深度测试片段着色器及模版测试之后执行。 片段着色器中内置变量gl_FragCoord的z值即为深度值。 提前深…...

阿里云服务器数据盘是什么?系统盘和数据盘区别
阿里云服务器系统盘和数据盘有什么区别?系统盘类似Windows电脑的C盘,数据盘相当于其他盘符,数据盘可以有多个而系统盘只能有一个,数据盘可有可无而云服务器系统盘是必须要有的。阿里云服务器网来详细说下阿里云服务器数据盘和系统…...
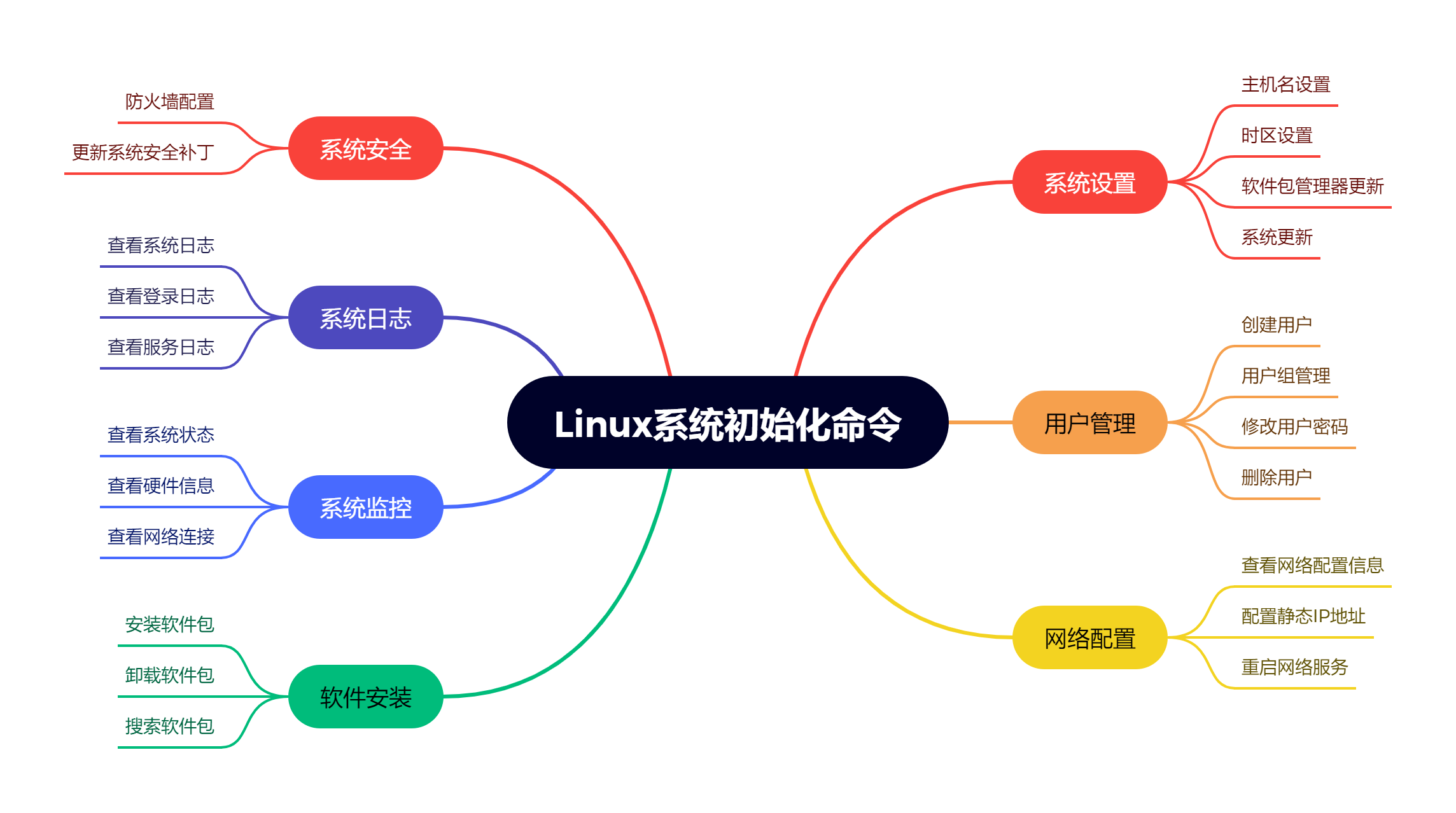
linux常用命令精选
参考文章: Top 60 Linux Interview Questions and Answers - howtouselinux 在管理和维护Linux系统时,有一些常用的命令可以帮助您进行系统初始化和配置。这些命令涵盖了各种任务,包括系统设置、用户管理、软件安装和网络配置等。 本文将为…...
人体行为足力特征分析及其应用研究_kaic
第一章 绪论 随着社会现代化的发展和科技的不断进步,我国航天事业蓬勃发展,与此同时产生了很多亟待解决的难题,康复医疗成为航天医学和康复领域的重要课题之一。载人航天实践证明,失重对航天员生理功能有很大影响,这不…...
javascript基础二十七:说说 JavaScript 数字精度丢失的问题,解决方案?
一、场景复现 一个经典的面试题 0.1 0.2 0.3 // false 为什么是false呢? 先看下面这个比喻 比如一个数 130.33333333… 这是一个除不尽的运算,3会一直无限循环,数学可以表示,但是计算机要存储,方便下次再使用,但…...
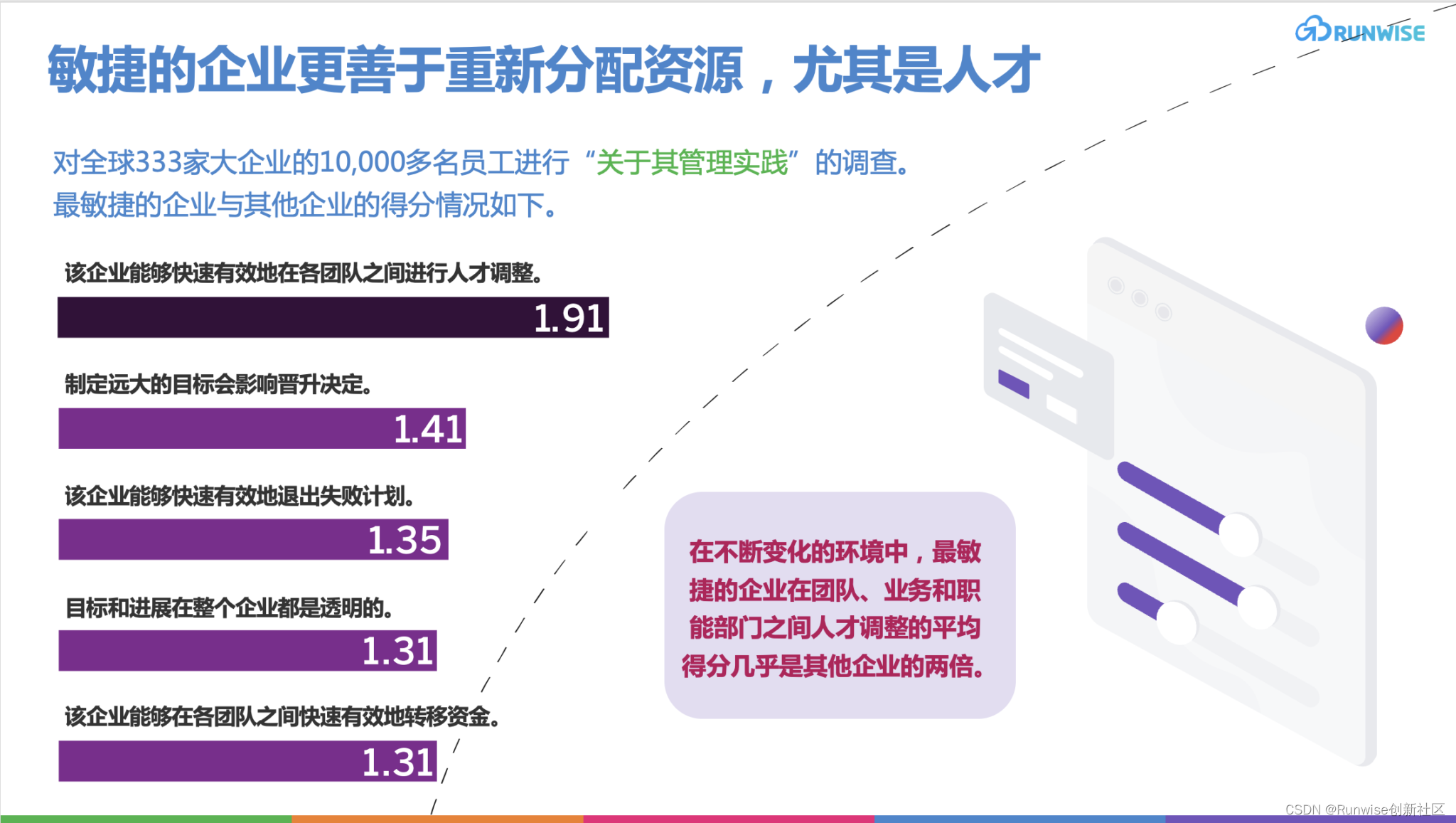
重塑工作场所:后疫情时代组织韧性的8个策略
经济寒冬来临,倒挂的收益率曲线、持续上升的利率以及层出不穷的裁员公告等等,让经济学家们得出一个结论:全球经济正在衰退。然而,经济下行周期可能是卓越公司改变其命运的最佳时机。有研究表明,相对于非经济衰退时期&a…...

TCP协议为什么要三次握手而不是两次?
TCP(Transmission Control Protocol,传输控制协议)的历史可以追溯到1970年代初期,最初的版本是RFC 793,后来经过多次更新和改进,包括RFC 1122、RFC 1323、RFC 2018、RFC 2581、RFC 2873、RFC 3168和RFC 461…...

使用Vuex进行状态管理
在Vue.js应用程序中,状态管理是一个重要的主题。当应用程序变得复杂,组件之间的状态共享和通信变得困难,这时候使用Vuex就会变得十分有用。Vuex是一个专门为Vue.js设计的状态管理库,它提供了一个集中式的状态管理方案,…...
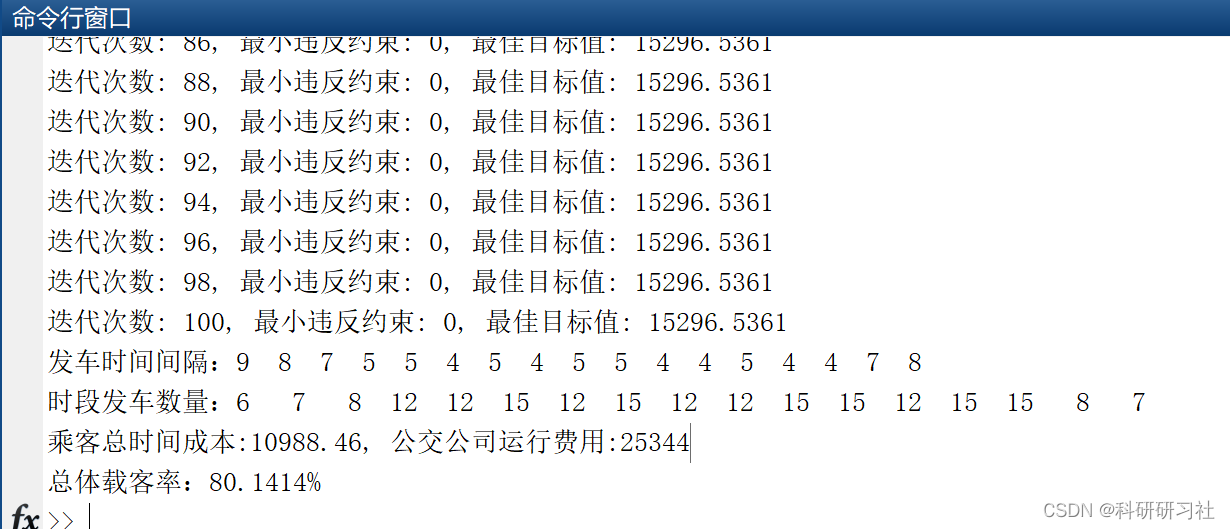
【优化调度】基于改进遗传算法的公交车调度排班优化的研究与实现(Matlab代码实现)
目录 1 概述 2 运行结果 3 参考文献 4 Matlab代码 1 概述 本文对当前公交企业调度系统进行了分析,建立了公交排班的数学模型。本文基于数据挖掘分析的结果上,使用截面客流量数据对模型进行约束,得出了公交客流出行的空间分布规律。再以…...
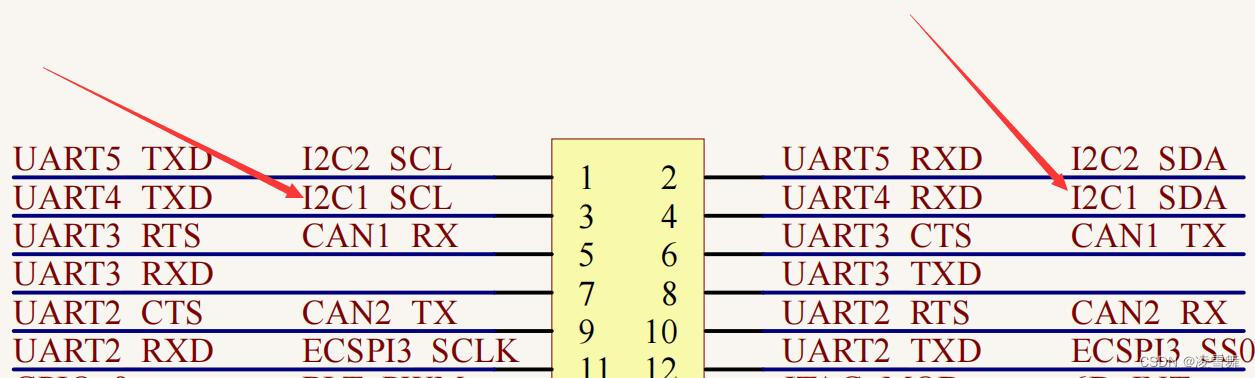
IMX6ULL裸机篇之I2C实验-硬件原理图
一. I2C 实验简介 I2C实验,我们就来学习如何使用 I.MX6U 的 I2C 接口来驱动 AP3216C,读取 AP3216C 的传感器数据。 AP3216C是一个三合一的环境光传感器,ALSPSIRLED,ALS是环境光,PS是接近传感器,IR是红外L…...

华为OD机试真题 Java 实现【获取字符串中连续出现次数第k多的字母的次数】【2023Q1 100分】,附详细解题思路
一、题目描述 给定一个字符串,只包含大写字母,求在包含同一字母的子串中,长度第 k 长的子串的长度,相同字母只取最长的那个子串。 二、输入描述 第一行有一个子串(1<长度<100),只包含大写字母;第二…...

充分统计量和因子分解定理
充分统计量 定义: 设样本 X X X的服从分布 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ,设 T T ( X ) TT(X) TT(X)为一统计量,若在已知 T T T的条件下,样本 X X X的条件分布与参数 θ \the…...

M1 PD安装arm ubuntu及Docker
M1 PD安装arm ubuntu 下载 Ubuntu 22.04.2 LTS https://cn.ubuntu.com/download/server/arm 参考视频安装 https://www.bilibili.com/video/BV1Mu4y1f74v/?spm_id_from333.999.0.0&vd_source9056c6d3c91a117baaceb663957daa08 PD Ubuntu安装docker 删除现有的docker安装…...

TCP协议的RST标志
下文中的内容多数来自【参考】中的文章,这边进行一个整理和总结,后续会慢慢增加出现各个 RST 包的测试代码,便于理解。 TCP的 “断开连接” 标志 RST 标志 Reset,复位标志,用于非正常地关闭连接。它是 TCP 协议首部里…...

【软件质量与软件测试 白盒测试与黑盒测试】
第十章 黑盒测试 10.1 等价类划分: 10.1.1 划分等价类 等价类是指所有数据中的一组,它们具有相同的测试结果或相同的响应。等价类划分是将输入数据分为多个等价类的过程。 10.1.2 划分等价类的方法 划分等价类方法主要包括以下几种: 特…...

JavaScript教程(高级)
面向对象编程介绍 两大编程思想 (1)、 面向过程编程: (缩写 POP)( Process-oriented programming)面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现&am…...
C++进阶 —— 范围for(C++11新特性)
目录 一,范围for介绍 二,范围for注意事项 一,范围for介绍 范围for(range-based for loop)是C11新引入的特性,可遍历各种序列结构的容器(如数组、vector、list等);每次循…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
