javascript基础二十七:说说 JavaScript 数字精度丢失的问题,解决方案?
一、场景复现
一个经典的面试题
0.1 + 0.2 === 0.3 // false
为什么是false呢?
先看下面这个比喻
比如一个数 1÷3=0.33333333…
这是一个除不尽的运算,3会一直无限循环,数学可以表示,但是计算机要存储,方便下次再使用,但0.333333… 这个数无限循环,再大的内存它也存不下,所以不能存储一个相对于数学来说的值,只能存储一个近似值,这么存储后再取出时自然就出现精度丢失问题
二、浮点数
“浮点数”是一种表示数字的标准,整数也可以用浮点数的格式来存储
我们也可以理解成,浮点数就是小数
在JavaScript中,现在主流的数值类型是Number,而Number采用的是IEEE754规范中64位双精度浮点数编码
这样的存储结构优点是可以归一化处理整数和小数,节省存储空间
对于一个整数,可以很轻易转化成十进制或者二进制。但是对于一个浮点数来说,因为小数点的存在,小数点的位置不是固定的。解决思路就是使用科学计数法,这样小数点位置就固定了
而计算机只能用二进制(0或1)表示,二进制转换为科学记数法的公式如下:
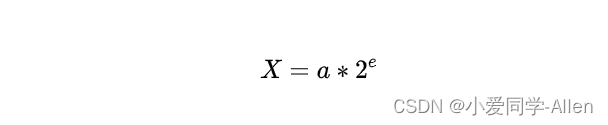
其中,a的值为0或者1,e为小数点移动的位置
举个粟子:
27.0转化成二进制为11011.0 ,科学计数法表示为:

前面讲到,javaScript存储方式是双精度浮点数,其长度为8个字节,即64位比特
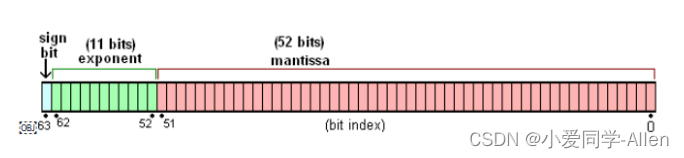
64位比特又可分为三个部分:
- 符号位S:第 1 位是正负数符号位(sign),0代表正数,1代表负数
- 指数位E:中间的 11 位存储指数(exponent),用来表示次方数,可以为正负数。在双精度浮点数中,指数的固定偏移量为1023
- 尾数位M:最后的 52 位是尾数(mantissa),超出的部分自动进一舍零
如下图:
二、问题分析
再回到问题上
0.1 + 0.2 === 0.3 // false
通过上面的学习,我们知道,在javascript语言中,0.1 和 0.2 都转化成二进制后再进行运算
// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111// 转成十进制正好是 0.30000000000000004
所以输出false
再来一个问题,那么为什么x=0.1得到0.1?
主要是存储二进制时小数点的偏移量最大为52位,最多可以表达的位数是2^53=9007199254740992,对应科学计数尾数是 9.007199254740992,这也是 JS 最多能表示的精度
它的长度是 16,所以可以使用 toPrecision(16) 来做精度运算,超过的精度会自动做凑整处理
.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000,去掉末尾的零后正好为 0.1
但看到的 0.1 实际上并不是 0.1。不信你可用更高的精度试试:
0.1.toPrecision(21) = 0.100000000000000005551
如果整数大于 9007199254740992 会出现什么情况呢?
由于指数位最大值是1023,所以最大可以表示的整数是 2^1024 - 1,这就是能表示的最大整数。但你并不能这样计算这个数字,因为从 2^1024 开始就变成了 Infinity
> Math.pow(2, 1023)
8.98846567431158e+307> Math.pow(2, 1024)
Infinity
那么对于 (2^53, 2^63) 之间的数会出现什么情况呢?
- (2^53, 2^54) 之间的数会两个选一个,只能精确表示偶数
- (2^54, 2^55) 之间的数会四个选一个,只能精确表示4个倍数
- … 依次跳过更多2的倍数
要想解决大数的问题你可以引用第三方库 bignumber.js,原理是把所有数字当作字符串,重新实现了计算逻辑,缺点是性能比原生差很多
小结
计算机存储双精度浮点数需要先把十进制数转换为二进制的科学记数法的形式,然后计算机以自己的规则{符号位+(指数位+指数偏移量的二进制)+小数部分}存储二进制的科学记数法
因为存储时有位数限制(64位),并且某些十进制的浮点数在转换为二进制数时会出现无限循环,会造成二进制的舍入操作(0舍1入),当再转换为十进制时就造成了计算误差
三、解决方案
理论上用有限的空间来存储无限的小数是不可能保证精确的,但我们可以处理一下得到我们期望的结果
当你拿到 1.4000000000000001 这样的数据要展示时,建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示,如下:
parseFloat(1.4000000000000001.toPrecision(12)) === 1.4 // True
封装成方法就是:
function strip(num, precision = 12) {
return +parseFloat(num.toPrecision(precision));
}
对于运算类操作,如 ±*/,就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。以加法为例:
/*** 精确加法*/
function add(num1, num2) {const num1Digits = (num1.toString().split('.')[1] || '').length;const num2Digits = (num2.toString().split('.')[1] || '').length;const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));return (num1 * baseNum + num2 * baseNum) / baseNum;
}
最后还可以使用第三方库,如Math.js、BigDecimal.js
也可以使用以下的方法
相关文章:

javascript基础二十七:说说 JavaScript 数字精度丢失的问题,解决方案?
一、场景复现 一个经典的面试题 0.1 0.2 0.3 // false 为什么是false呢? 先看下面这个比喻 比如一个数 130.33333333… 这是一个除不尽的运算,3会一直无限循环,数学可以表示,但是计算机要存储,方便下次再使用,但…...
重塑工作场所:后疫情时代组织韧性的8个策略
经济寒冬来临,倒挂的收益率曲线、持续上升的利率以及层出不穷的裁员公告等等,让经济学家们得出一个结论:全球经济正在衰退。然而,经济下行周期可能是卓越公司改变其命运的最佳时机。有研究表明,相对于非经济衰退时期&a…...

TCP协议为什么要三次握手而不是两次?
TCP(Transmission Control Protocol,传输控制协议)的历史可以追溯到1970年代初期,最初的版本是RFC 793,后来经过多次更新和改进,包括RFC 1122、RFC 1323、RFC 2018、RFC 2581、RFC 2873、RFC 3168和RFC 461…...

使用Vuex进行状态管理
在Vue.js应用程序中,状态管理是一个重要的主题。当应用程序变得复杂,组件之间的状态共享和通信变得困难,这时候使用Vuex就会变得十分有用。Vuex是一个专门为Vue.js设计的状态管理库,它提供了一个集中式的状态管理方案,…...
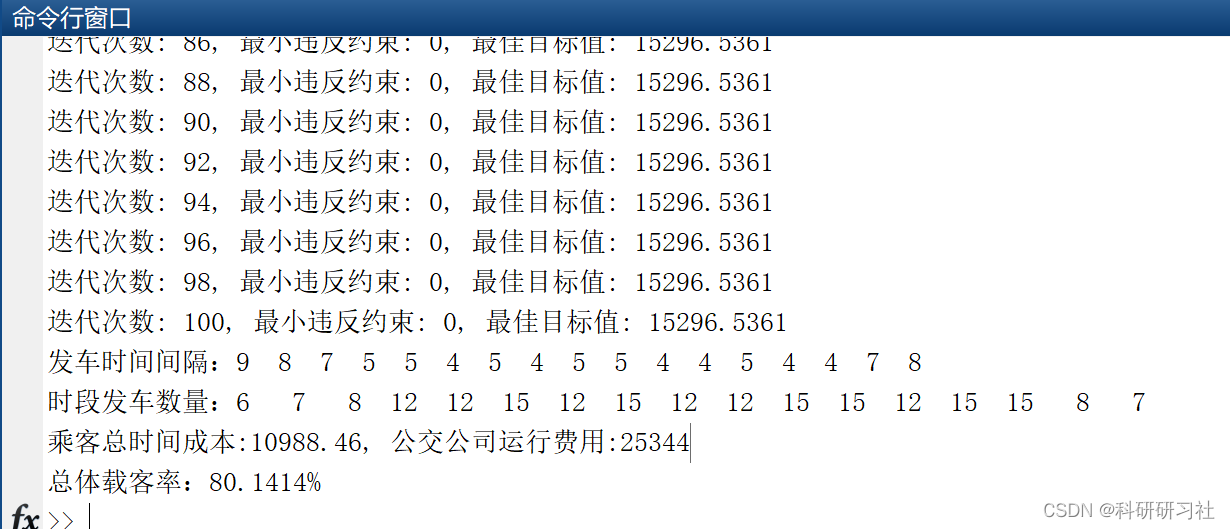
【优化调度】基于改进遗传算法的公交车调度排班优化的研究与实现(Matlab代码实现)
目录 1 概述 2 运行结果 3 参考文献 4 Matlab代码 1 概述 本文对当前公交企业调度系统进行了分析,建立了公交排班的数学模型。本文基于数据挖掘分析的结果上,使用截面客流量数据对模型进行约束,得出了公交客流出行的空间分布规律。再以…...
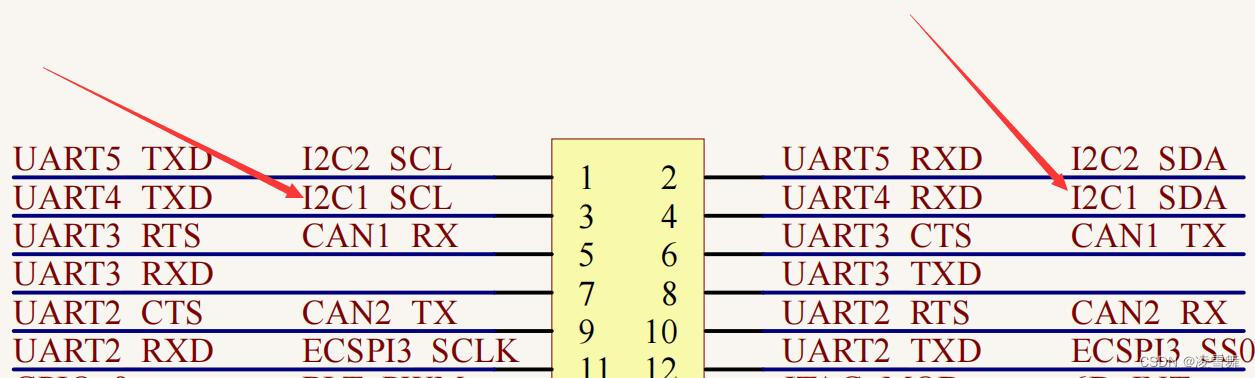
IMX6ULL裸机篇之I2C实验-硬件原理图
一. I2C 实验简介 I2C实验,我们就来学习如何使用 I.MX6U 的 I2C 接口来驱动 AP3216C,读取 AP3216C 的传感器数据。 AP3216C是一个三合一的环境光传感器,ALSPSIRLED,ALS是环境光,PS是接近传感器,IR是红外L…...

华为OD机试真题 Java 实现【获取字符串中连续出现次数第k多的字母的次数】【2023Q1 100分】,附详细解题思路
一、题目描述 给定一个字符串,只包含大写字母,求在包含同一字母的子串中,长度第 k 长的子串的长度,相同字母只取最长的那个子串。 二、输入描述 第一行有一个子串(1<长度<100),只包含大写字母;第二…...

充分统计量和因子分解定理
充分统计量 定义: 设样本 X X X的服从分布 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ,设 T T ( X ) TT(X) TT(X)为一统计量,若在已知 T T T的条件下,样本 X X X的条件分布与参数 θ \the…...

M1 PD安装arm ubuntu及Docker
M1 PD安装arm ubuntu 下载 Ubuntu 22.04.2 LTS https://cn.ubuntu.com/download/server/arm 参考视频安装 https://www.bilibili.com/video/BV1Mu4y1f74v/?spm_id_from333.999.0.0&vd_source9056c6d3c91a117baaceb663957daa08 PD Ubuntu安装docker 删除现有的docker安装…...

TCP协议的RST标志
下文中的内容多数来自【参考】中的文章,这边进行一个整理和总结,后续会慢慢增加出现各个 RST 包的测试代码,便于理解。 TCP的 “断开连接” 标志 RST 标志 Reset,复位标志,用于非正常地关闭连接。它是 TCP 协议首部里…...

【软件质量与软件测试 白盒测试与黑盒测试】
第十章 黑盒测试 10.1 等价类划分: 10.1.1 划分等价类 等价类是指所有数据中的一组,它们具有相同的测试结果或相同的响应。等价类划分是将输入数据分为多个等价类的过程。 10.1.2 划分等价类的方法 划分等价类方法主要包括以下几种: 特…...

JavaScript教程(高级)
面向对象编程介绍 两大编程思想 (1)、 面向过程编程: (缩写 POP)( Process-oriented programming)面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现&am…...
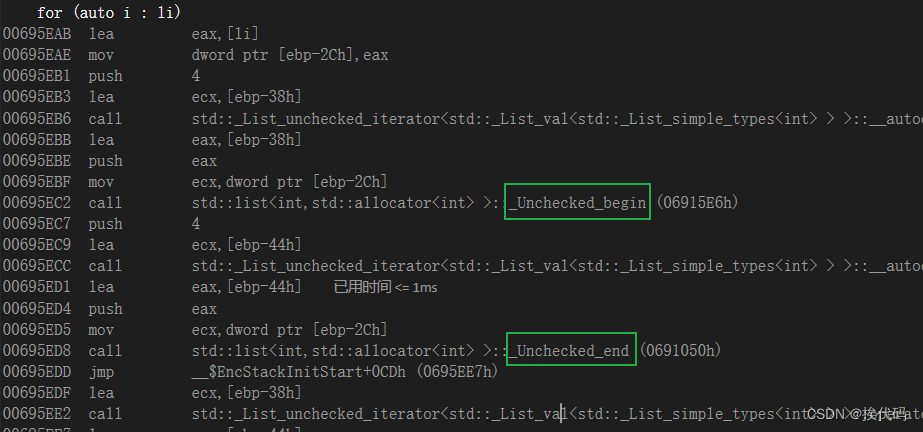
C++进阶 —— 范围for(C++11新特性)
目录 一,范围for介绍 二,范围for注意事项 一,范围for介绍 范围for(range-based for loop)是C11新引入的特性,可遍历各种序列结构的容器(如数组、vector、list等);每次循…...

ELK +Filebeat日志分析系统
一、 ELK日志分析系统概述 1、ELK简介 ELK是三个开源软件的缩写,分别表示:Elasticsearch , Logstash, Kibana , 它们都是开源软件。新增了一个FileBeat,它是一个轻量级的日志收集处理工具(Agent),Filebeat占用资源少,…...

万字解析PELT算法!
Linux是一个通用操作系统的内核,她的目标是星辰大海,上到网络服务器,下至嵌入式设备都能运行良好。做一款好的linux进程调度器是一项非常具有挑战性的任务,因为设计约束太多了: 它必须是公平的快速响应系统的throughp…...
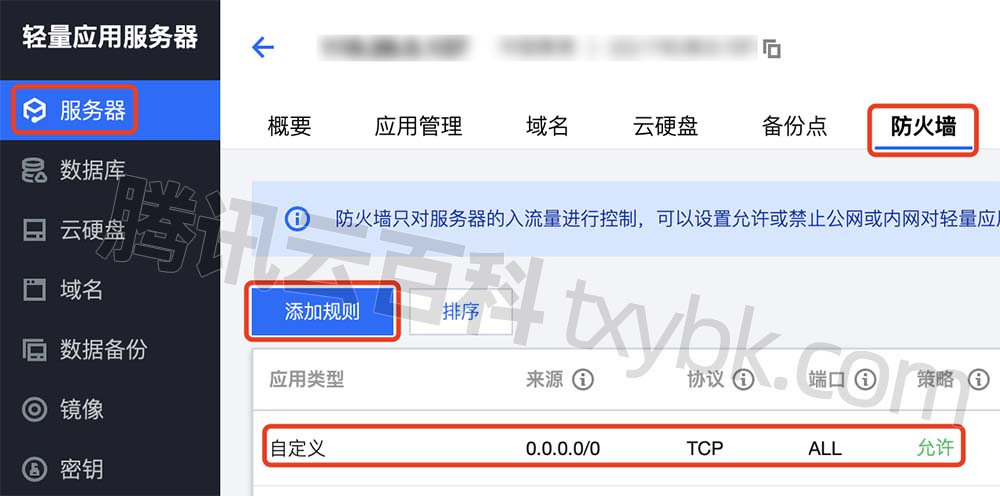
腾讯云服务器端口怎么全开?教程来了
腾讯云服务器端口怎么全开?云服务器CVM在安全组中设置开通,轻量应用服务器在防火墙中设置,腾讯云百科来详细说下腾讯云服务器端口全开放教程: 目录 腾讯云服务器端口全部开通教程 云服务器CVM端口全开放教程 轻量应用服务器开…...

深入理解Java虚拟机:JVM高级特性与最佳实践-总结-13
深入理解Java虚拟机:JVM高级特性与最佳实践-总结-13 Java内存模型与线程Java内存模型原子性、可见性与有序性先行发生原则 Java内存模型与线程 Java内存模型 原子性、可见性与有序性 Java内存模型是围绕着在并发过程中如何处理原子性、可见性和有序性这三个特征来…...

租售keysight E8257D 50G模拟信号发生器 销售/回收
是德(Keysight) E8257D 模拟信号发生器 Keysight E8257D (Agilent) PSG 模拟信号发生器提供业界领先的输出功率、电平精度和高达 67 GHz 的相位噪声性能(工作频率可达 70 GHz)。Agilent PSG 模拟信号发生器的高输出功率和卓越的电…...
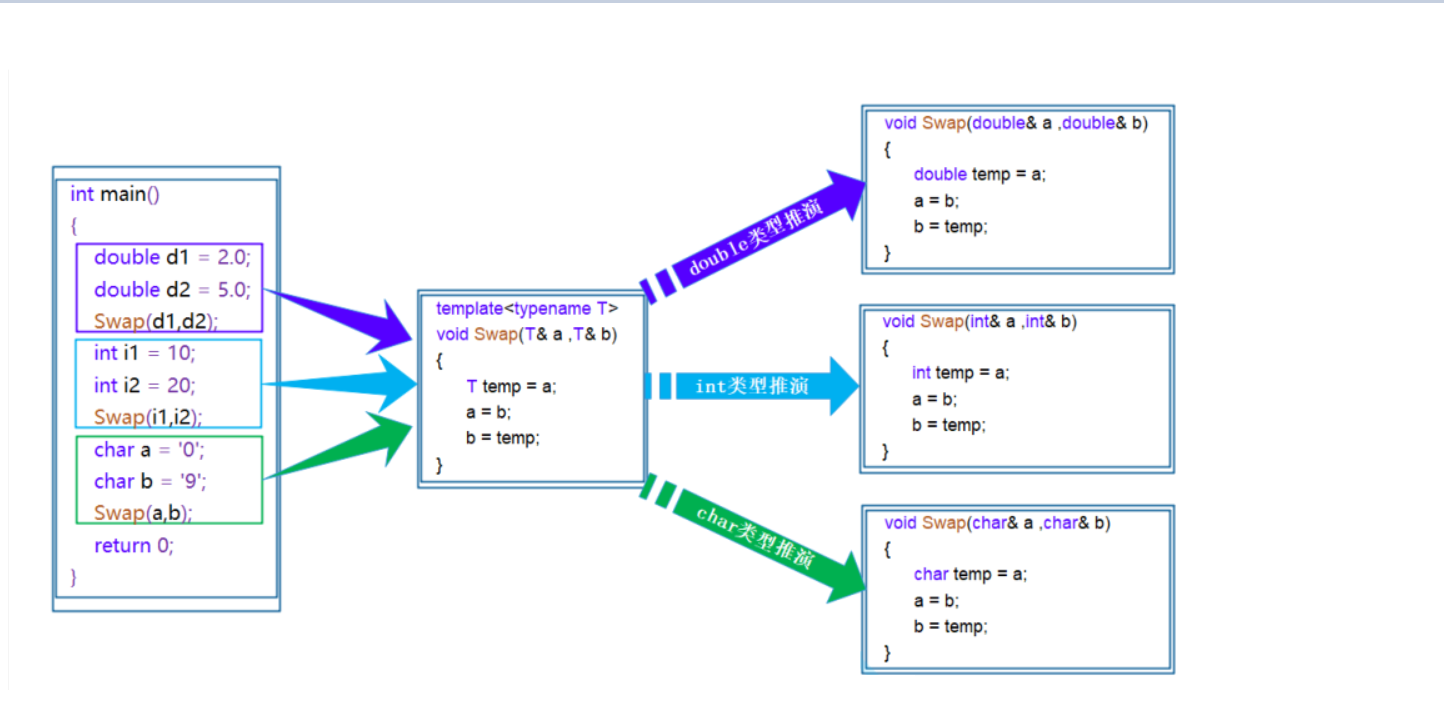
【C++】什么是函数模板/类模板?
文章目录 一、函数模板1.什么是函数模板?2.函数模板格式3.函数模板原理4.函数模板实例化(1)隐式实例化(2)显示实例化 二.类模板1.类模板定义格式2.类模板的实例化 总结 一、函数模板 1.什么是函数模板? 函…...

为什么是ChatGPT引发了AI浪潮?
目录 BERT和GPT简介 BERT和GPT核心差异 GPT的优势 GPT的劣势 总结 随着近期ChatGPT的火热,引发各行各业都开始讨论AI,以及AI可以如何应用到各个细分场景。为了不被时代“抛弃”,我也投入了相当的精力用于研究和探索。但在试验的过程中&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
