充分统计量和因子分解定理
充分统计量
-
定义: 设样本 X X X的服从分布 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ,设 T = T ( X ) T=T(X) T=T(X)为一统计量,若在已知 T T T的条件下,样本 X X X的条件分布与参数 θ \theta θ无关,则称 T = T ( X ) T=T(X) T=T(X)为 θ \theta θ的充分统计量
-
Example:
设 X = ( x 1 , x 2 , . . , x n ) X=(x_1,x_2,..,x_n) X=(x1,x2,..,xn)是从泊松分布 P ( λ ) P(\lambda) P(λ)中抽取的随机样本,下面将从定义出发证明 T ( X ) = ∑ i = 1 n x i T(X)=\sum_{i=1}^nx_i T(X)=∑i=1nxi是 θ \theta θ的充分统计量∵ x i ∼ P ( λ ) , ∴ ∑ i = 1 n x i ∼ P ( n λ ) \because x_i \sim P(\lambda),\therefore\sum_{i=1}^nx_i \sim P(n\lambda) ∵xi∼P(λ),∴∑i=1nxi∼P(nλ),我们将其记为 T ∼ P ( θ ) , θ = n λ T\sim P(\theta),\theta=n\lambda T∼P(θ),θ=nλ
由已知可得,样本的条件分布为 f ( X ∣ λ ) = ∏ i = 1 n e − λ λ x i x i ! = e − n λ λ ∑ i = 1 n x i ∏ i = 1 n x i ! = e − θ λ T ∏ i = 1 n x i ! f(X|\lambda)=\prod_{i=1}^n\frac{e^{-\lambda}\lambda^{x_i}}{x_i!}=\frac{e^{-n\lambda}\lambda^{\sum_{i=1}^nx_i}}{\prod_{i=1}^nx_i!}=\frac{e^{-\theta}\lambda^{T}}{\prod_{i=1}^nx_i!} f(X∣λ)=i=1∏nxi!e−λλxi=∏i=1nxi!e−nλλ∑i=1nxi=∏i=1nxi!e−θλT
此时样本 X X X的条件分布 f ( X ∣ λ ) f(X|\lambda) f(X∣λ)与参数 λ \lambda λ无关,因此 T ( X ) = ∑ i = 1 n x i T(X)=\sum_{i=1}^nx_i T(X)=∑i=1nxi是 θ \theta θ的充分统计量
因子分解定理
-
从定义出发证明充分统计量显得有些繁琐,因此我们引入因子分解定理
-
定义: 设样本 X = ( x 1 , x 2 , . . , x n ) X=(x_1,x_2,..,x_n) X=(x1,x2,..,xn)的条件分布为 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ, T = T ( X ) T=T(X) T=T(X)为一统计量,则 T = T ( X ) T=T(X) T=T(X)是充分统计量的充分必要条件为条件分布为 f ( X ∣ θ ) f(X|\theta) f(X∣θ)可被分解为如下形式: f ( X ∣ θ ) = g ( T ( X ) , θ ) ⋅ h ( X ) f(X|\theta)=g(T(X),\theta)·h(X) f(X∣θ)=g(T(X),θ)⋅h(X)也就是可被分解为两部分,一部分仅与 T ( X ) T(X) T(X)和 θ \theta θ有关,另一部分为一个常数或仅与样本 X X X有关。
-
重要推论: 若 T = T ( X ) T=T(X) T=T(X)是充分统计量, S = g ( T ) S=g(T) S=g(T)是 T T T一一对应的变换,则 S S S也是 θ \theta θ的充分统计量
-
Example:
证明以下命题:设 X = ( x 1 , x 2 , . . , x n ) X=(x_1,x_2,..,x_n) X=(x1,x2,..,xn)为从正态总体 N ( a , σ 2 ) N(a,\sigma^2) N(a,σ2)中抽取的随机样本,令 θ = ( a , σ 2 ) \theta=(a,\sigma^2) θ=(a,σ2),则 T ( X ) = ( ∑ x i , ∑ x i 2 ) T(X)=(\sum{x_i},\sum{x_{i}^2}) T(X)=(∑xi,∑xi2)为充分统计量,且 ( X ‾ , S 2 ) (\overline{X},S^2) (X,S2)也是充分统计量,此处 X ‾ = 1 n ∑ x i , S 2 = 1 n − 1 ∑ ( x i − X ‾ ) 2 \overline{X}=\frac{1}{n}\sum{x_i},S^2=\frac{1}{n-1}\sum{(x_i-\overline{X})^2} X=n1∑xi,S2=n−11∑(xi−X)2由已知得,样本的条件分布为
f ( x ) = ( 1 2 π σ ) n exp ( − 1 2 σ 2 ∑ ( x i − a ) 2 ) = ( 1 2 π σ ) n exp ( − 1 2 σ 2 ( ∑ x i 2 − 2 a ∑ x i + n a 2 ) ) = g ( T ( X ) , θ ) ⋅ h ( X ) \begin{aligned} f(x) &= (\frac{1}{\sqrt{2\pi}\sigma})^n\exp(-\frac{1}{2\sigma^2}\sum{(x_i-a)^2}) \\ &=(\frac{1}{\sqrt{2\pi}\sigma})^n\exp(-\frac{1}{2\sigma^2}(\sum{x_i^2}-2a\sum{x_i}+na^2)) \\ &= g(T(X),\theta)·h(X) \end{aligned} f(x)=(2πσ1)nexp(−2σ21∑(xi−a)2)=(2πσ1)nexp(−2σ21(∑xi2−2a∑xi+na2))=g(T(X),θ)⋅h(X)
此处的 h ( X ) ≡ 1 h(X)\equiv1 h(X)≡1,至此, T ( X ) = ( ∑ x i , ∑ x i 2 ) T(X)=(\sum{x_i},\sum{x_{i}^2}) T(X)=(∑xi,∑xi2)为充分统计量得证,又因为 ( X ‾ , S 2 ) (\overline{X},S^2) (X,S2)为 T ( X ) = ( ∑ x i , ∑ x i 2 ) T(X)=(\sum{x_i},\sum{x_{i}^2}) T(X)=(∑xi,∑xi2)一一对应的变换,由推论可得, ( X ‾ , S 2 ) (\overline{X},S^2) (X,S2)也是充分统计量
理解:
- 充分统计量对于简化计算是有显著的帮助的
- 一一对应的变换可理解为一个函数
- 样本的条件分布其实就是样本似然
- 无论是从定义出发证明充分统计量,还是通过因子分解定理,都需要先求出样本的条件分布,然后再选择一种方法
- 从定义出发证明需要想方设法消除式子中原来的参数
相关文章:

充分统计量和因子分解定理
充分统计量 定义: 设样本 X X X的服从分布 f ( X ∣ θ ) f(X|\theta) f(X∣θ), θ ∈ Θ \theta\in\Theta θ∈Θ,设 T T ( X ) TT(X) TT(X)为一统计量,若在已知 T T T的条件下,样本 X X X的条件分布与参数 θ \the…...

M1 PD安装arm ubuntu及Docker
M1 PD安装arm ubuntu 下载 Ubuntu 22.04.2 LTS https://cn.ubuntu.com/download/server/arm 参考视频安装 https://www.bilibili.com/video/BV1Mu4y1f74v/?spm_id_from333.999.0.0&vd_source9056c6d3c91a117baaceb663957daa08 PD Ubuntu安装docker 删除现有的docker安装…...

TCP协议的RST标志
下文中的内容多数来自【参考】中的文章,这边进行一个整理和总结,后续会慢慢增加出现各个 RST 包的测试代码,便于理解。 TCP的 “断开连接” 标志 RST 标志 Reset,复位标志,用于非正常地关闭连接。它是 TCP 协议首部里…...

【软件质量与软件测试 白盒测试与黑盒测试】
第十章 黑盒测试 10.1 等价类划分: 10.1.1 划分等价类 等价类是指所有数据中的一组,它们具有相同的测试结果或相同的响应。等价类划分是将输入数据分为多个等价类的过程。 10.1.2 划分等价类的方法 划分等价类方法主要包括以下几种: 特…...

JavaScript教程(高级)
面向对象编程介绍 两大编程思想 (1)、 面向过程编程: (缩写 POP)( Process-oriented programming)面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现&am…...
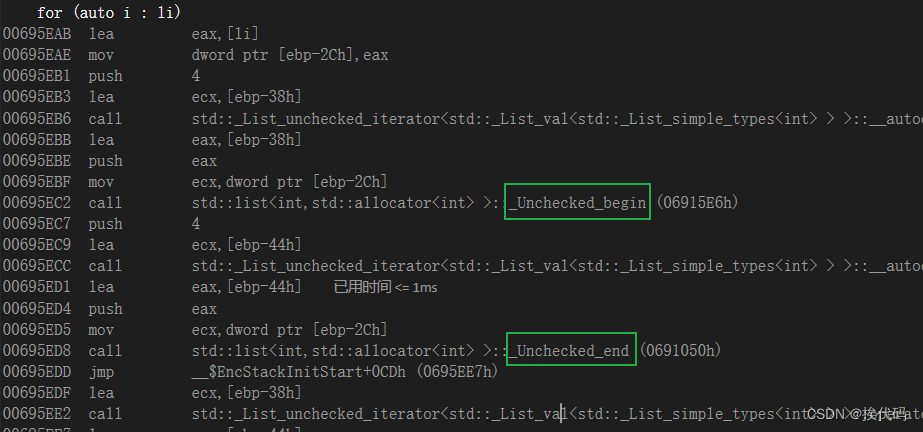
C++进阶 —— 范围for(C++11新特性)
目录 一,范围for介绍 二,范围for注意事项 一,范围for介绍 范围for(range-based for loop)是C11新引入的特性,可遍历各种序列结构的容器(如数组、vector、list等);每次循…...

ELK +Filebeat日志分析系统
一、 ELK日志分析系统概述 1、ELK简介 ELK是三个开源软件的缩写,分别表示:Elasticsearch , Logstash, Kibana , 它们都是开源软件。新增了一个FileBeat,它是一个轻量级的日志收集处理工具(Agent),Filebeat占用资源少,…...

万字解析PELT算法!
Linux是一个通用操作系统的内核,她的目标是星辰大海,上到网络服务器,下至嵌入式设备都能运行良好。做一款好的linux进程调度器是一项非常具有挑战性的任务,因为设计约束太多了: 它必须是公平的快速响应系统的throughp…...
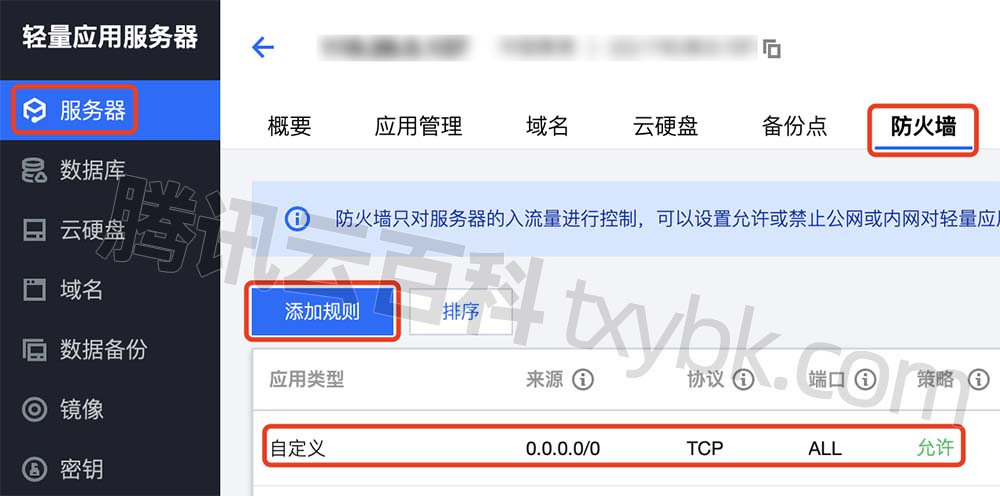
腾讯云服务器端口怎么全开?教程来了
腾讯云服务器端口怎么全开?云服务器CVM在安全组中设置开通,轻量应用服务器在防火墙中设置,腾讯云百科来详细说下腾讯云服务器端口全开放教程: 目录 腾讯云服务器端口全部开通教程 云服务器CVM端口全开放教程 轻量应用服务器开…...

深入理解Java虚拟机:JVM高级特性与最佳实践-总结-13
深入理解Java虚拟机:JVM高级特性与最佳实践-总结-13 Java内存模型与线程Java内存模型原子性、可见性与有序性先行发生原则 Java内存模型与线程 Java内存模型 原子性、可见性与有序性 Java内存模型是围绕着在并发过程中如何处理原子性、可见性和有序性这三个特征来…...

租售keysight E8257D 50G模拟信号发生器 销售/回收
是德(Keysight) E8257D 模拟信号发生器 Keysight E8257D (Agilent) PSG 模拟信号发生器提供业界领先的输出功率、电平精度和高达 67 GHz 的相位噪声性能(工作频率可达 70 GHz)。Agilent PSG 模拟信号发生器的高输出功率和卓越的电…...
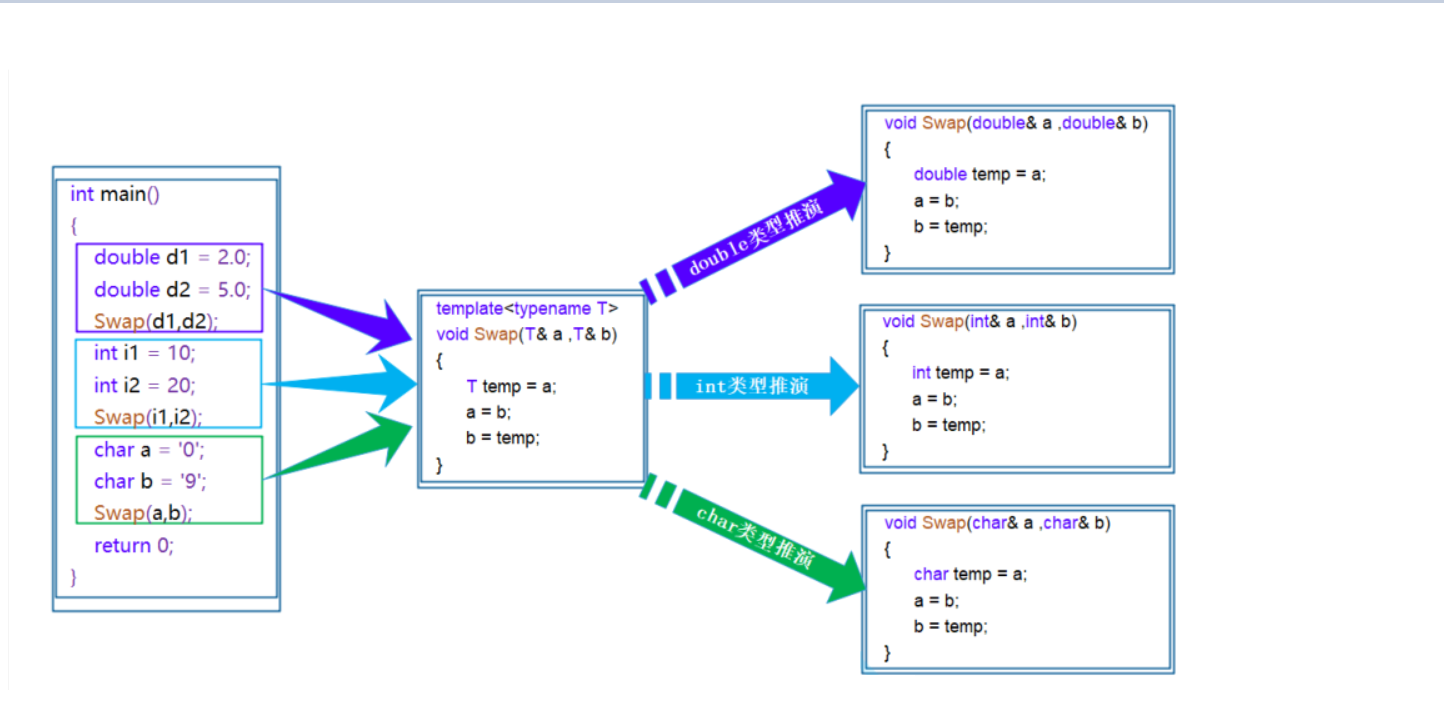
【C++】什么是函数模板/类模板?
文章目录 一、函数模板1.什么是函数模板?2.函数模板格式3.函数模板原理4.函数模板实例化(1)隐式实例化(2)显示实例化 二.类模板1.类模板定义格式2.类模板的实例化 总结 一、函数模板 1.什么是函数模板? 函…...

为什么是ChatGPT引发了AI浪潮?
目录 BERT和GPT简介 BERT和GPT核心差异 GPT的优势 GPT的劣势 总结 随着近期ChatGPT的火热,引发各行各业都开始讨论AI,以及AI可以如何应用到各个细分场景。为了不被时代“抛弃”,我也投入了相当的精力用于研究和探索。但在试验的过程中&…...
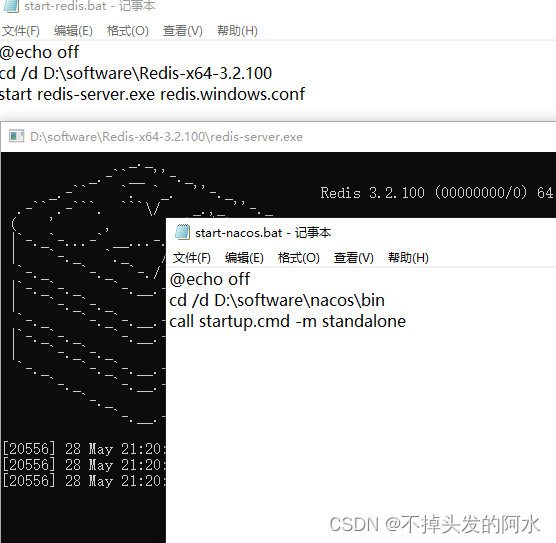
批处理文件(.bat)启动redis及任何软件(同理)
批处理文件 每次从文件根目录用配置文件格式来启动redis太麻烦了 可以在桌面上使用批处理文件(.bat)启动Redis,请按照以下步骤进行操作: 打开文本编辑器,如记事本。 在编辑器中输入以下内容: 将文件保存…...

深度学习求解稀疏最优控制问题的并行化算法
稀疏最优控制问题 问题改编自论文An FE-Inexact Heterogeneous ADMM for Elliptic Optimal Control Problems with L1-Control Cost { min y ( μ ) , u ( μ )...

牛客网项目—开发社区首页
视频连接:开发社区首页_哔哩哔哩_bilibili 代码地址:Community: msf begin 仿牛客论坛项目 (gitee.com) 本文是对仿牛客论坛项目的学习,学习本文之前需要了解Java开发的常用框架,例如SpringBoot、Mybatis等等。如果你也在学习牛…...

uniapp水文【uniapp】
文章目录 1、前言2、历史3、发展4、功能5、优缺点6、总结7、附录7.1、高频使用7.2、使用注意 1、前言 Uniapp是一种跨平台的移动应用开发框架,它允许开发者使用一套代码库,同时生成iOS、Android等多个平台的应用程序。这种技术方案可以大大降低开发成本…...

Java函数式接口
3 函数式接口 3.1 函数式接口概述 函数式接口:有且仅有一个抽象方法的接口 Java中的函数式编程体现就是Lambda表达式,所以函数式接口就是可以适用于Lambda使用的接口只有确保接口中有且仅有一个抽象方法, Java中的Lambda才能顺利地进行推导…...

安装libevent库
安装libevent库 yum install libevent libevent-devel 自动安装Memcached yum install memcached 源码安装 下载1.6.19版本 wget https://www.memcached.org/files/memcached-1.6.19.tar.gz (若证书过期yum install -y ca-certificates) 解压源码 tar -zxvf…...

vue 截取字符串的方法
vue中的字符串方法,我目前使用最多的是下面两种方法,因为 vue的字符串方法支持断言操作。 1、 vue中截取字符串的方法如下: 2、 vue中截取字符串的方法,这个方法也是需要依赖于 vue库提供的支持。 3、 vue中截取字符串的方法&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
