PriorityBlockingQueue无界阻塞优先级队列
PriorityBlockingQueue无界阻塞优先级队列
PriorityBlockingQueue 是带优先级的无界阻塞队列,每次出队都返回优先级最高的元素,是二叉树最小堆的实
现,研究过数组方式存放最小堆节点的都知道,直接遍历队列元素是无序的。
如图 PriorityBlockingQueue 内部有个数组 queue 用来存放队列元素,size 用来存放队列元素个数,allocationSpinLockOffset是用来在扩容队列时候做cas的,目的是保证只有一个线程可以进行扩容。
由于这是一个优先级队列所以有个比较器comparator用来比较元素大小。lock独占锁对象用来控制同时只能有一个线程可以进行入队出队操作。notEmpty条件变量用来实现take方法阻塞模式。这里没有notFull 条件变量是因为这里的put操作是非阻塞的,为啥要设计为非阻塞的是因为这是无界队列。
最后PriorityQueue q用来搞序列化的。
如下构造函数,默认队列容量为11,默认比较器为null;
private static final int DEFAULT_INITIAL_CAPACITY = 11;
public PriorityBlockingQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityBlockingQueue(int initialCapacity) {
this(initialCapacity, null);
}
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
this.comparator = comparator;
this.queue = new Object[initialCapacity];
}
PriorityBlockingQueue方法
✓ Offer操作
在队列插入一个元素,由于是无界队列,所以一直为成功返回true;
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
final ReentrantLock lock = this.lock;
lock.lock();
int n, cap;
Object[] array;
//如果当前元素个数>=队列容量,则扩容(1)
while ((n = size) >= (cap = (array = queue).length))
tryGrow(array, cap);
try {
Comparator<? super E> cmp = comparator;
//默认比较器为null
if (cmp == null)(2)
siftUpComparable(n, e, array);
else
//自定义比较器(3)
siftUpUsingComparator(n, e, array, cmp);
//队列元素增加1,并且激活notEmpty的条件队列里面的一个阻塞线程
size = n + 1;(9)
notEmpty.signal();
} finally {
lock.unlock();
}
return true;
}
主流程比较简单,下面看看两个主要函数
private void tryGrow(Object[] array, int oldCap) {
lock.unlock(); //must release and then re-acquire main lock Object[] newArray = null;
//cas成功则扩容(4)
if (allocationSpinLock == 0 &&
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) {
try {
//oldGap<64则扩容新增oldcap+2,否者扩容50%,并且最大为MAX_ARRAY_SIZE int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // grow faster if small
(oldCap >> 1));
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
int minCap = oldCap + 1;
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
newCap = MAX_ARRAY_SIZE;
}
if (newCap > oldCap && queue == array)
newArray = new Object[newCap];
} finally {
allocationSpinLock = 0;
}
}
//第一个线程cas成功后,第二个线程会进入这个地方,然后第二个线程让出cpu,尽量让第一个线程执行下面点获取锁,但
是这得不到肯定的保证。(5)
if (newArray == null) // back off if another thread is allocating Thread.yield();
lock.lock();(6)
if (newArray != null && queue == array) {
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
tryGrow 目的是扩容,这里要思考下为啥在扩容前要先释放锁,然后使用 cas 控制只有一个线程可以扩容成功。
我的理解是为了性能,因为扩容时候是需要花时间的,如果这些操作时候还占用锁那么其他线程在这个时候是不能进
行出队操作的,也不能进行入队操作,这大大降低了并发性。
所以在扩容前释放锁,这允许其他出队线程可以进行出队操作,但是由于释放了锁,所以也允许在扩容时候进行
入队操作,这就会导致多个线程进行扩容会出现问题,所以这里使用了一个spinlock用cas控制只有一个线程可以进
行扩容,失败的线程调用Thread.yield()让出cpu,目的意在让扩容线程扩容后优先调用lock.lock重新获取锁,但是
这得不到一定的保证,有可能调用Thread.yield()的线程先获取了锁。
那copy元素数据到新数组为啥放到获取锁后面那?原因应该是因为可见性问题,因为queue并没有被volatile修
饰。另外有可能在扩容时候进行了出队操作,如果直接拷贝可能看到的数组元素不是最新的。而通过调用Lock后,获
取的数组则是最新的,并且在释放锁前 数组内容不会变化。
具体建堆算法:
private static <T> void siftUpComparable(int k, T x, Object[] array) { Comparable<? super T> key = (Comparable<? super T>) x;
//队列元素个数>0则判断插入位置,否者直接入队(7)
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = array[parent];
if (key.compareTo((T) e) >= 0)
break;
array[k] = e;
k = parent;
}
array[k] = key;(8)
}
下面用图说话模拟下过程:
假设队列容量为2
• 第一次offer(2)时候
执行(1)为false所以执行(2),由于k=n=size=0;所以执行(8)元素入队,然执行(9)size+1;
执行(1)为false,所以执行(2)由于k=1,所以进入while循环,parent=0;e=2;key=4;key>e所以break;然后把4存到数据下标为1的地方,这时候队列状态为:
• 第三次offer(4)时候
执行(1)为true,所以调用tryGrow,由于2<64所以newCap=2 + (2+2)=6;然后创建新数组并拷贝,然后调用siftUpComparable;k=2>0进入循环 parent=0;e=2;key=6;key>e所以break;然后把6放入下标为2的地方,现在队列状态:
• 第四次offer(1)时候
执行(1)为false,所以执行(2)由于k=3,所以进入while循环,parent=0;e=2;key=1; key<e;所以把2
复制到数组下标为3的地方,然后k=0退出循环;然后把2存放到下标为0地方,现在状态:
✓ Poll操作
在队列头部获取并移除一个元素,如果队列为空,则返回null
public E poll() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return dequeue();
} finally {
lock.unlock();
}
}
主要看dequeue
private E dequeue() {
//队列为空,则返回null
int n = size - 1;
if (n < 0)
return null;
else {
//获取队头元素(1)
Object[] array = queue;
E result = (E) array[0];
//获取对尾元素,并值null(2)
E x = (E) array[n];
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)//cmp=null则调用这个,把对尾元素位置插入到0位置,并且调整堆为最小堆(3) siftDownComparable(0, x, array, n);
else
siftDownUsingComparator(0, x, array, n, cmp);
size = n;(4)
return result;
}
}
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) {
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = array[child];(5)
int right = child + 1;(6)
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)(7) c = array[child = right];
if (key.compareTo((T) c) <= 0)(8)
break;
array[k] = c;
k = child;
}
array[k] = key;(9)
}
}
下面用图说话模拟下过程:
• 第一次调用poll()
首先执行(1) result=1;然后执行(2)x=2;这时候队列状态
下面重点说说siftDownComparable这个屌屌的建立最小堆的算法:
首先说下思想,其中k一开始为0,x为数组里面最后一个元素,由于第0个元素为树根,被出队时候要被搞掉,所以建堆要从它的左右孩子节点找一个最小的值来当树根,子树根被搞掉后,会找子树的左右孩子最小的元素来代替,直到树节点为止,还不明白,没关系,看图说话:
假如当前队列元素:
然后看leftChildVal = 4;rightChildVal = 6; 4<6;所以c=4;也就是获取根节点的左右孩子值小的那一个; 然后看
11>4也就是key>c;然后把c放入树根,现在树为:
然后看根的左边孩子4为根的子树我们要为这个字树找一个根节点。
看leftChildVal = 8;rightChildVal = 10; 8<10;所以c=8;也就是获取根节点的左右孩子值小的那一个; 然后看11>8也就是key>c;然后把c放入树根,现在树为:
这时候k=3;half=3所以推出循环,执行(9)后结果为:
这时候队列为:
✓ Put操作
内部调用的offer,由于是无界队列,所以不需要阻塞
public void put(E e) {
offer(e); // never need to block
}
✓ Take操作
获取队列头元素,如果队列为空则阻塞。
public E take() throws InterruptedException {
final ReentrantLock lock = this.lock;
lock.lockInterruptibly();
E result;
try {
//如果队列为空,则阻塞,把当前线程放入notEmpty的条件队列
while ( (result = dequeue()) == null)
notEmpty.await();
} finally {
lock.unlock();
}
return result;
}
这里是阻塞实现,阻塞后直到入队操作调用notEmpty.signal 才会返回。
✓ Size操作
获取队列元个数,由于加了独占锁所以返回结果是精确的
public int size() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return size;
} finally {
lock.unlock();
}
}
PriorityBlockingQueue小结
PriorityBlockingQueue类似于ArrayBlockingQueue内部使用一个独占锁来控制同时只有一个线程可以进行入队和出队,另外前者只使用了一个 notEmpty 条件变量而没有 notFull这是因为前者是无界队列,当put 时候永远不会处于await所以也不需要被唤醒。
PriorityBlockingQueue 始终保证出队的元素是优先级最高的元素,并且可以定制优先级的规则,内部通过使用一个二叉树最小堆算法来维护内部数组,这个数组是可扩容的,当当前元素个数>=最大容量时候会通过算法扩容。
值得注意的是为了避免在扩容操作时候其他线程不能进行出队操作,实现上使用了先释放锁,然后通过 cas 保证同时只有一个线程可以扩容成功。
PriorityBlockingQueue示例
PriorityBlockingQueue类是JDK提供的优先级队列 本身是线程安全的 内部使用显示锁 保证线程安全。
PriorityBlockingQueue 存储的对象必须是实现 Comparable 接口的 因为 PriorityBlockingQueue 队列会根据内部存储的每一个元素的 compareTo 方法比较每个元素的大小。这样在 take 出来的时候会根据优先级 将优先级最小的最先取出 。
下面是示例代码
public static PriorityBlockingQueue<User> queue = new PriorityBlockingQueue<User>();
public static void main(String[] args) {
queue.add(new User(1,"wu"));
queue.add(new User(5,"wu5"));
queue.add(new User(23,"wu23"));
queue.add(new User(55,"wu55"));
queue.add(new User(9,"wu9"));
queue.add(new User(3,"wu3"));
for (User user : queue) {
try {
System.out.println(queue.take().name);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
//静态内部类
static class User implements Comparable<User>{
public User(int age,String name) {
this.age = age;
this.name = name;
}
int age;
String name;
@Override
public int compareTo(User o) {
return this.age > o.age ? -1 : 1;
}
相关文章:

PriorityBlockingQueue无界阻塞优先级队列
PriorityBlockingQueue无界阻塞优先级队列 PriorityBlockingQueue 是带优先级的无界阻塞队列,每次出队都返回优先级最高的元素,是二叉树最小堆的实 现,研究过数组方式存放最小堆节点的都知道,直接遍历队列元素是无序的。 如图 P…...

「HTML和CSS入门指南」p 标签详解
<p> 标签是什么? HTML5 中的 <p> 标签是用于定义段落的标签。它可以用来标记文章、新闻等长篇内容中的段落,并且可以与其他 HTML 元素配合使用。 <p> 标签的语法和属性 <p> 标签的语法非常简单,只需要在 HTML 文件中插入 <p> 和 </p>…...
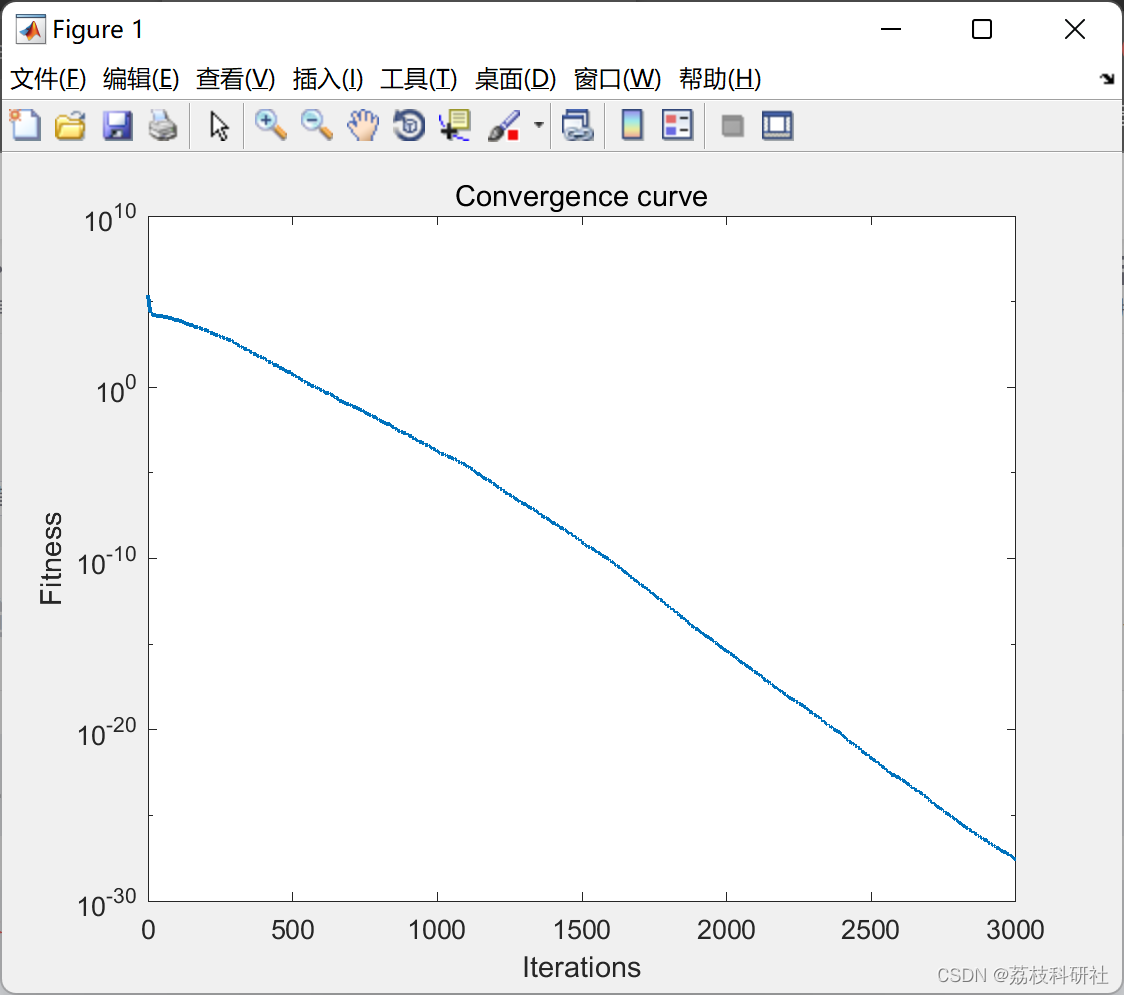
【单目标优化算法】孔雀优化算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

chatgpt赋能python:Python同一行多个语句:如何提高你的编程效率?
Python同一行多个语句:如何提高你的编程效率? Python是一种优雅的编程语言,拥有简洁易懂的语法,可以帮助你快速编写可以在各种领域使用的高级代码。其中,Python同一行多个语句,是一种可以大大提高编程效率…...
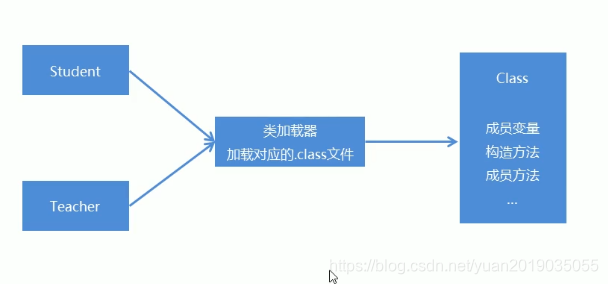
Java反射概述
2 反射 2.1 反射概述 Java反射机制:是指在运行时去获取一个类的变量和方法信息。然后通过获取到的信息来创建对象,调用方法的一种机制。由于这种动态性,可以极大的增强程序的灵活性,程序不用在编译期就完成确定,在运行期仍然可以扩展2.2 反射获取Class类的对象 我们要想通过反…...
)
《网络是怎样连接的》(一)
第一章web浏览器 简介 首先输入网址URL,浏览器进行解析,将我们需要哪些数据告诉服务器。浏览器向服务器发送消息,必须告诉操作系统的接收方的IP地址,所以浏览器先查出web服务器的IP地址,向DNS服务器查询域名对应的IP…...

Flink on yarn任务日志怎么看
1、jobmanager日志 在yarn上可以直接看 2、taskmanager日志 在flink的webui中可以看,但是flink任务失败后,webui就不存在了,那怎么看? 这是jobmanager的地址 hadoop02:19888/jobhistory/logs/hadoop02:45454/container_e03_16844…...
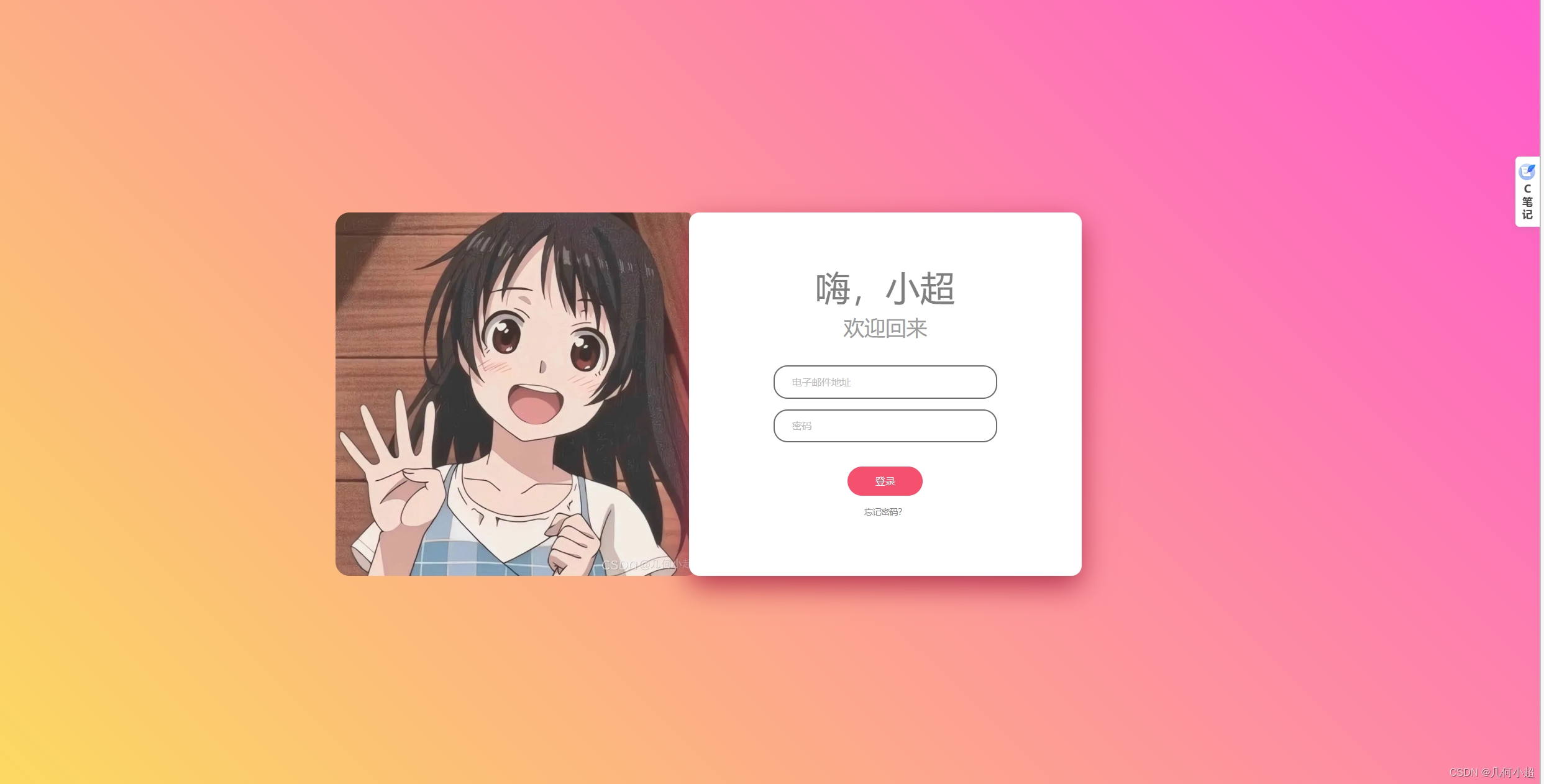
二次元的登录界面
今天还是继续坚持写博客,然后今天给大家带来比较具有二次元风格的登录界面,也只是用html和css来写的,大家可以来看看! 个人名片: 😊作者简介:一名大一在校生,web前端开发专业 &…...
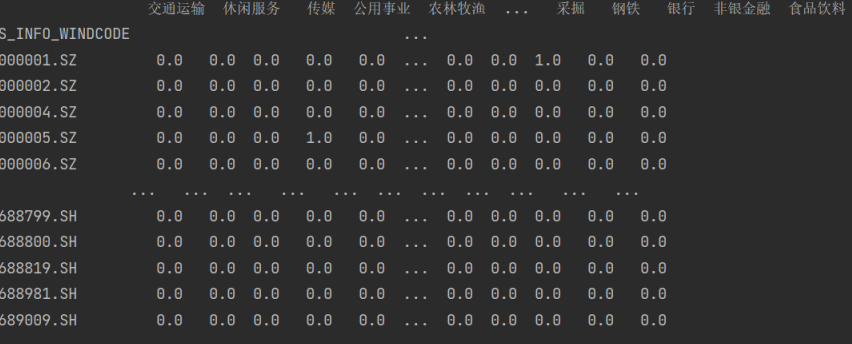
2. 量化多因子数据清洗——去极值、标准化、正交化、中性化
一、去极值 1. MAD MAD(mean absolute deviation)又称为绝对值差中位数法,是一种先需计算所有因子与平均值之间的距离总和来检测离群值的方法. def extreme_MAD(rawdata, n): median rawdata.quantile(0.5) # 找出中位数 new_median (abs(…...

皮卡丘反射型XSS
1.反射型xss(get) 进入反射型xss(get)的关卡,我们可以看到如下页面 先输入合法数据查看情况,例如输入“kobe” 再随便输入一个,比如我舍友的外号“xunlei”,“666”,嘿嘿嘿 F12查看源代码,发现你输入的数…...
巧计口诀-软件测试的生命周期,黑盒测试设计方法
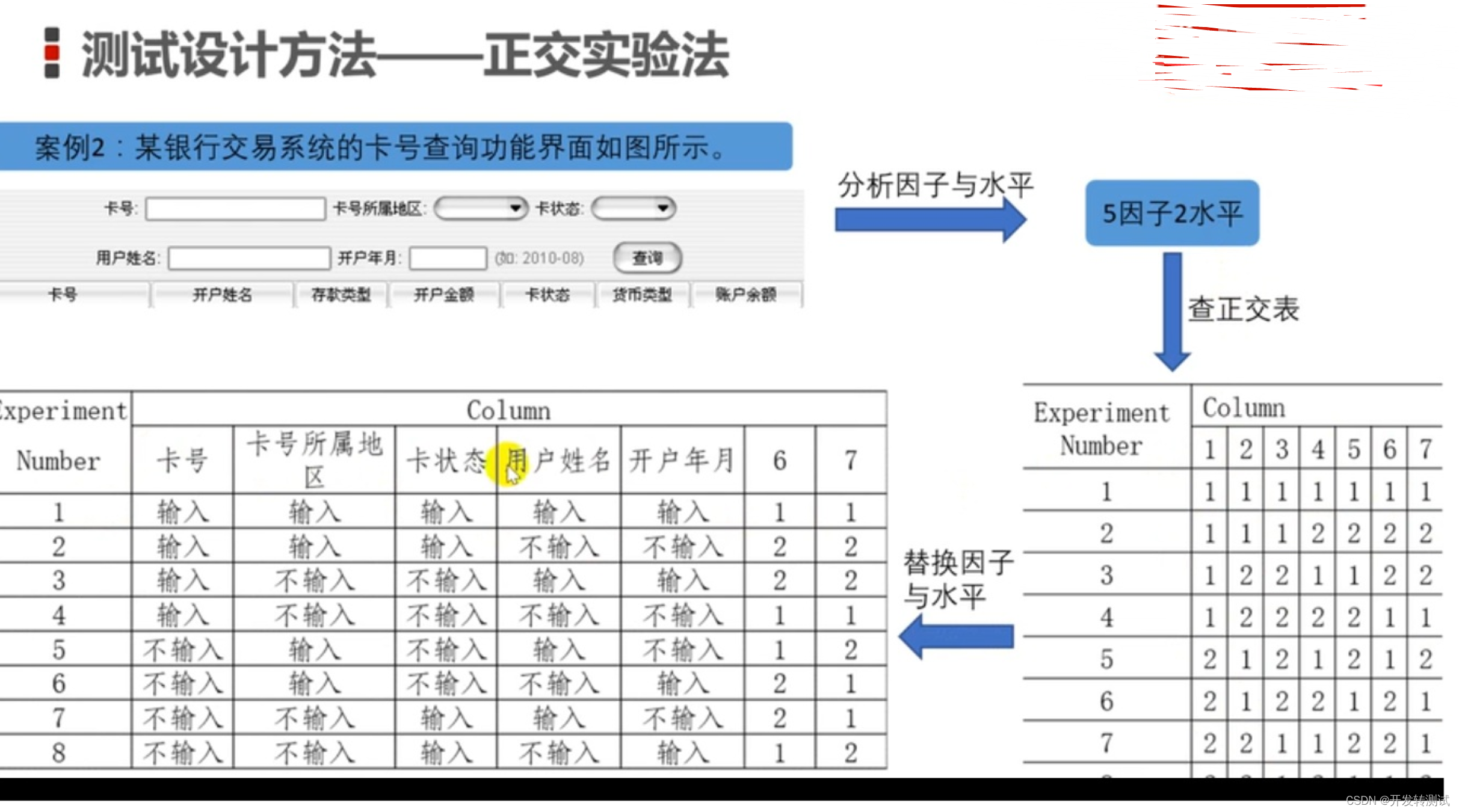
目录 1。口诀 2。黑盒设计方法适用场合 3。黑盒设计方法详解 3.1。等价类法 3.2。 边界值法 3.3。判定表法 3.4。因果表 3.5。状态迁移图 3.6。场景法 3.7。正交实验法 3.8。错误推断法 1。口诀 又到了找工作的日子,背诵这些基本知识和概念又开始了。我找…...
- Ashmem驱动)
Android系统的Ashmem匿名共享内存系统分析(1)- Ashmem驱动
声明 其实对于Android系统的Ashmem匿名共享内存系统早就有分析的想法,记得2019年6、7月份Mr.Deng离职期间约定一起对其进行研究的,但因为我个人问题没能实施这个计划,留下些许遗憾…文中参考了很多书籍及博客内容,可能涉及的比较…...

Redis 事务详细介绍
事务 注意:Redis单条命令是保证原子性的;但是事务不保证原子性! Redis事务没有隔离级别的概念,所有的命令在事务中,并没有直接被执行,只有发起执行命令时才执行 Redis事务本质:一组命令的集合&…...

2023-5-29第二十九天
consult咨询,查阅,商讨 specialize专门从事,专攻 inspect检查 pattern图案,方式 optimize使最优化 ensemble整体,全体 subscript下标 subscribe签名 sector行业,部门 precedence优先,优…...
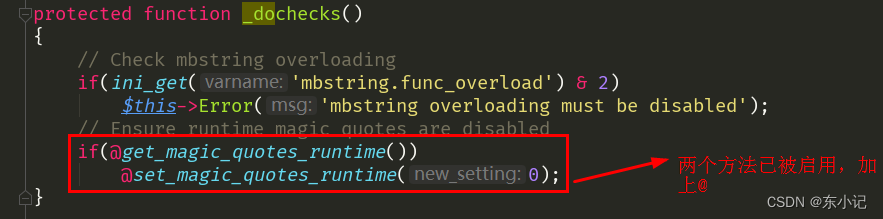
【第三方库】PHP实现创建PDF文件和编辑PDF文件
目录 引入Setasign/fpdf、Setasign/fpdi 解决写入中文时乱码问题 1.下载并放置中文语言包(他人封装):https://github.com/DCgithub21/cd_FPDF 2.编写并运行生成字体文件的程序文件(addFont.php) 中文字体举例&…...

线程的回收及内存演示
ps -elf|grep mthread 查看进程和线程 top -p 6513 查看内存 一、线程的回收 使用pthread_join 函数: #include <pthread.h> int pthread_join(pthread_t thread, void **retval); 注意:pthread_join 是阻塞函数,如果回收的线…...

高精度倾角传感器测量原理
高精度倾角传感器测量原理技术参数 1.性能参数 测量范围:0~30 测量精度:0.06 分 辨 率:0.0001 测量方向:X,Y 时间漂移:0.08/月 更新时间:30ms 上电启动时间:0.5s 2.电…...

Android 12 init流程分析
前言 刚开始接触需要了解的概念理解过程遇到了什么问题代码的位置和流程分析如何分析和调试遇到的问题 基本的概念 .rc 文件 这个文件在Android framework 中服务相关代码可以看到。类似surfaceflinger.rc 、mediaserver.rc等等。 在这些rc里面定义了某一个service࿰…...

【Python小技巧】Python操控Chrome浏览器实现网页打开、切换、关闭(送独家Chrome操作打包类源码、Chrome浏览器Cookie在哪里?)
文章目录 前言一、什么时候需要用Python控制浏览器?二、下载Chrome浏览器驱动文件1. 安装Chrome浏览器并查看版本2. 下载浏览器驱动文件3. 解压到python编译器目录(python.exe所在目录) 三、Python控制Chrome浏览器(附源代码&…...

数据在内存中的存储
目录 一、数据类型的介绍 1.C语言基本内置类型 2.类型基本归类 1.整形 2.浮点型 3.构造类型 4.指针类型 二、整形在内存中的存储 三、浮点数在内次中的存储 1.存储形式 2.对M、E的特殊规定 (1)对M的特殊规定 (2)对E的…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
