[NOIP2015 提高组] 运输计划
题目链接
给定一棵树以及树上的 m m m 条通路,我们可以在树上选取一条边,将其权重置为 0 0 0,目标是
min 将某条边权重置 0 max 通路权重 . \min_{将某条边权重置 0}\max 通路权重. 将某条边权重置0minmax通路权重.
20pts(m=1)
当 m = 1 m=1 m=1 时,我们只需要求出树上的一条链上的权重和与权重最大值即可。
50pts
考虑一种暴力的算法,枚举将哪一条边权重置 0 0 0,然后重新在树上求解 m m m 条通路的权重。这个过程可以用 LCA 优化。任选一个结点为根,预处理出每一条通路的两个端点的 LCA,则路径长度可以通过树上差分快速计算。时间复杂度为 O ( n ( n + m ) ) O(n(n+m)) O(n(n+m))。
80pts(树退化为链)
当树退化为链时,这就是一个纯粹的数据结构问题。这类最小化最大值的问题可以考虑二分答案,将其转化为判定问题。给定一个权重上界 w w w 后,我们可以 O ( m ) O(m) O(m) 算出哪些通路的权重是超过这个上界的,而这些通路全部位于一条链上,因此我们可以 O ( m ) O(m) O(m) 求出它们的交集。然后在交集中找到权重最大的一条边,如果将这条边的权重置 0 0 0 后,所有通路的权重均不超过 w w w,那么 w w w 就是一个可行的上界。
100pts
上面的二分答案方法给了我们初步的思路。现在只需考虑树上给定权重上界后如何判定:首先任取一个结点作为根结点,并将边权下推为点权。使用差分维护数组 f [ v ] f[v] f[v] 表示从 v v v 的父结点到 v v v 的这条边被经过了多少次。假设有 c n t cnt cnt 个权重超过上届的通路,那么我们只要考虑被经过 c n t cnt cnt 次的边即可。代码如下:
#include<bits/stdc++.h>
using namespace std;const int maxn = 3e5 + 10;struct edge
{int v, w;int nxt;
} e[maxn << 1];
int n, m,
ver[maxn], w[maxn], a[maxn], b[maxn], c[maxn], d[maxn], f[maxn], s[maxn], num,
top[maxn], fa[maxn], size[maxn], son[maxn], dep[maxn], dis[maxn],
l, r, mid, ans, maxw;inline void adde(int u, int v, int w)
{static int ed = 1;e[++ed] = (edge){ v, w, ver[u] };ver[u] = ed;
}inline void dfs1(int u, int f)
{s[++num] = u;size[u] = 1, fa[u] = f;for(int i = ver[u]; i; i = e[i].nxt){int v = e[i].v;if(size[v])continue;dep[v] = dep[u] + 1;w[v] = e[i].w;dis[v] = dis[u] + w[v];dfs1(v, u);size[u] += size[v];if(size[son[u]] < size[v])son[u] = v;}
}inline void dfs2(int u, int t)
{top[u] = t;if(son[u])dfs2(son[u], t);for(int i = ver[u]; i; i = e[i].nxt){int v = e[i].v;if(v == fa[u] || v == son[u])continue;dfs2(v, v);}
}inline int lca(int u, int v)
{while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]])swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}inline bool check(int k)
{memset(f, 0, sizeof f);int cnt = 0;for(int i = 1; i <= m; i++){if(d[i] <= k)continue;f[a[i]]++, f[b[i]]++, f[c[i]] -= 2;cnt++;}for(int i = n; i >= 1; i--){f[fa[s[i]]] += f[s[i]];if(w[s[i]] >= maxw - k && f[s[i]] == cnt)return true;}return false;
}inline int read()
{static int x;static char c;x = 0, c = getchar();while(!isdigit(c))c = getchar();while(isdigit(c))x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();return x;
}int main()
{n = read(), m = read();for(int i = 1; i < n; i++){int u = read(), v = read(), w = read();adde(u, v, w);adde(v, u, w);l = max(l, w);}dep[1] = 1;dfs1(1, 0);dfs2(1, 1);for(int i = 1; i <= m; i++){a[i] = read(), b[i] = read();c[i] = lca(a[i], b[i]);d[i] = dis[a[i]] + dis[b[i]] - (dis[c[i]] << 1);r = max(r, d[i]);}maxw = r, l = maxw - l, r++;while(l <= r){mid = (l + r) >> 1;if(check(mid))ans = mid, r = mid - 1;elsel = mid + 1;}printf("%d", ans);return 0;
}
相关文章:

[NOIP2015 提高组] 运输计划
题目链接 给定一棵树以及树上的 m m m 条通路,我们可以在树上选取一条边,将其权重置为 0 0 0,目标是 min 将某条边权重置 0 max 通路权重 . \min_{将某条边权重置 0}\max 通路权重. 将某条边权重置0minmax通路权重. 20pts(m1) 当…...

【GreendDao 】RxQuery根据指定条件查询,完成后处理UI逻辑
GreenDao 和 RxJava 结合使用可以更方便地处理数据查询和 UI 逻辑的交互。RxQuery 使得一次查询结果可以直接转化成 Observable,而通过 RxJava 的操作符,可以方便地完成异步查询和 UI 逻辑的交互。以下是一个根据指定条件查询数据,查询完成后…...

【C++】unordered_set 和 unordered_map 使用 | 封装
文章目录 1. 使用1. unordered_set的使用2. unordered_map的使用 2. 封装修改结构定义针对insert参数 data的两种情况复用 哈希桶的insertKeyOfT模板参数的作用 迭代器operator()beginendunordered_set对于 begin和end的复用unordered_map对于 begin和end的复用unordered_map中…...

C++环形缓冲区设计与实现:从原理到应用的全方位解析
C环形缓冲区设计与实现:从原理到应用的全方位解析 一、环形缓冲区基础理论解析(Basic Theory of Circular Buffer)1.1 环形缓冲区的定义与作用(Definition and Function of Circular Buffer)1.2 环形缓冲区的基本原理&…...

阿里云服务器部署flask简单方法
记录如何在阿里云服务器上部署flask接口并实现公网访问。 文章目录 1. 简介2. 部署python3环境3. 生成requirement.txt4. 将项目打包上传5. 安装依赖库6. 查看防火墙7. 测试能否公网访问 1. 简介 因落地通话callback服务测试,需要我写一个测试demo,用于…...

【JavaSE】Java基础语法(二十三):递归与数组的高级操作
文章目录 1. 递归1.1 递归1.2 递归求阶乘 2. 数组的高级操作2.1 二分查找2.2 冒泡排序2.3 快速排序2.4 Arrays (应用) 1. 递归 1.1 递归 递归的介绍 以编程的角度来看,递归指的是方法定义中调用方法本身的现象把一个复杂的问题层层转化为一个与原问题相似的规模较…...
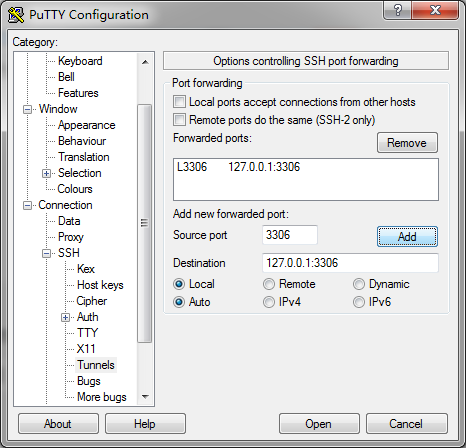
HUSTOJ使用指南
如何快速上手(了解系统的功能)? admin管理员用户登录,点击右上角管理,仔细阅读管理首页的说明。 切记:题目导入后一次只能删一题,不要导入过多你暂时用不上的题目,正确的方式是每次…...

java基础学习
一、注释 1)当行注释 // 2)多行注释 /* ... */ 3)文档注释 (java特有) /** author 张三 version v1.0 这是文档注释,需要将class用public修饰 */ 二、关键字 (1)48个关键…...
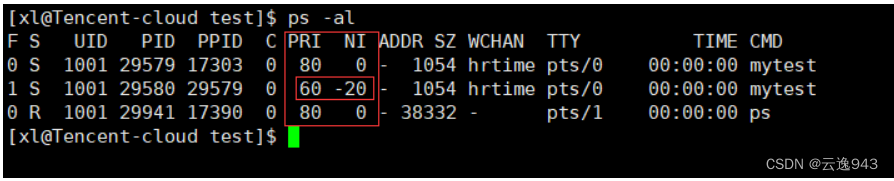
Linux——进程优先级
1.什么是优先级? 优先级和权限息息相关。权限的含义为能还是不能做这件事。而优先级则表示:你有权限去做,只不过是先去做还是后去做这件事罢了。 2.为什么会存在优先级? 优先级表明了狼多肉少的理念,举个例子ÿ…...

音频设备初始化与输出:QT与SDL策略模式的实现
音频设备初始化与输出:QT与SDL策略模式的实现 一、引言(Introduction)1.1 音频设备初始化与输出的重要性1.2 QT与SDL的音频设备处理1.3 策略模式在音频设备处理中的应用 二、深入理解音频设备初始化与输出2.1 音频设备的基本概念2.2 音频设备…...

Linux 手动部署 SpringBoot 项目
Linux 手动部署 SpringBoot 项目 1. 将项目打包成 jar 包 (1)引入插件 <build><plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId></pl…...

华为OD机试真题B卷 Java 实现【内存资源分配】
一、题目描述 有一个简易内存池,内存按照大小粒度分类,每个粒度有若干个可用内存资源,用户会进行一系列内存申请,需要按需分配内存池中的资源,返回申请结果成功失败列表。 分配规则如下: 分配的内存要大于等于内存的申请量,存在满足需求的内存就必须分配,优先分配粒度…...

深入理解ChatGPT插件:competitorppcads、seoanalysis和kraftful
1. 引言 插件,作为一种扩展功能的工具,为我们的应用程序提供了无限的可能性。在ChatGPT中,我们有许多强大的插件,如competitorppcads、seoanalysis和kraftful。这篇博客将详细介绍这三个插件的功能和使用方法。 2. competitorpp…...

通过源码编译安装LAMP平台的搭建
目录 1. 编译安装Apache httpd服务2 编写mysqld服务3 编译安装PHP 解析环境安装论坛 LAMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件,能够提供动态Web站点服务及其应用开发环境。 LAMP是一个缩写词,具体包…...
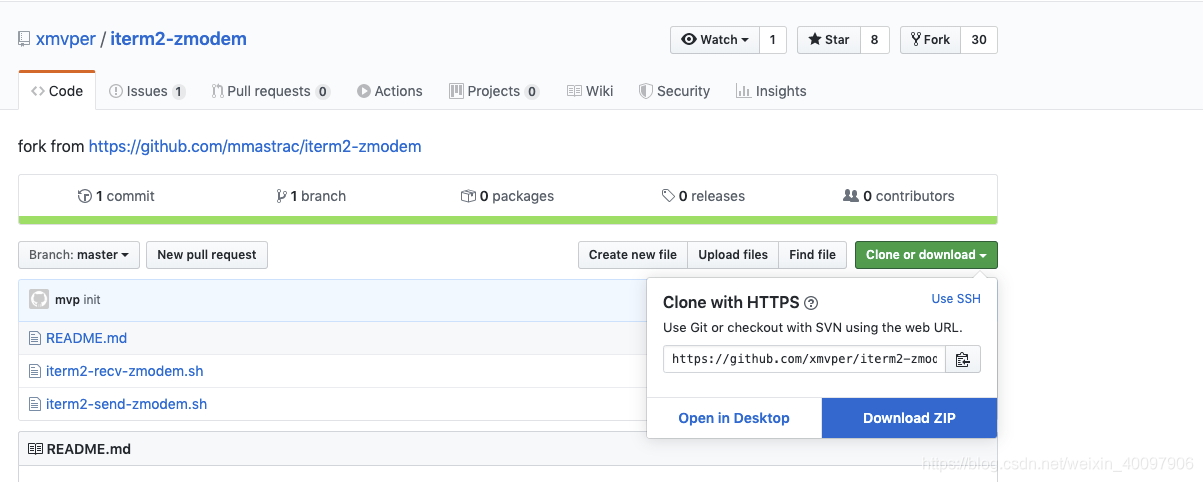
mac os 安装rz/sz
说明:使用rz sz实现终端的文件传输,该命令主要使用场景为 macos中通过堡垒机登陆后无法使用ftp工具传输文件。 工具:iTerm2、lrzsz、homebrew 以及两个脚本文件(iterm2-recv-zmodem.sh、iterm2-send-zmodem.sh) …...
 建立监听服务和开启事件循环)
Redis源码(1) 建立监听服务和开启事件循环
Redis 是cs架构(服务端-客户端),典型的一对多的服务器应用程序。多个客户通过网络与Redis服务器进行通信。那么在linux环境中是使用epoll(我们也 只讨论linux环境的,便于学习)。 通过使用I/O多路复用技术, redis 服务器使用单线程单进程的…...

c++基础概念,const与指针、引用的关系,auto,decltype关键字能干啥总得了解吧。总得按照需求自定义创建实体类,自己编写头文件吧
const限定符 有时我们希望定义这样一种变量,它的值不能被改变。例如,用一个变量来表示缓冲区的大小。使用变量的好处是当我们觉得缓冲区大小不再合适时,很容易对其进行调整。另一方面,也应随时警惕防止程序一不小心改变了这个值。…...

【数据结构】---几分钟简单几步学会手撕链式二叉树(下)
文章目录 前言🌟一、二叉树链式结构的实现🌏1.1 二叉树叶子节点个数💫代码:💫流程图: 🌏1.2 二叉树的高度💫第一种写法(不支持):📒代码:…...
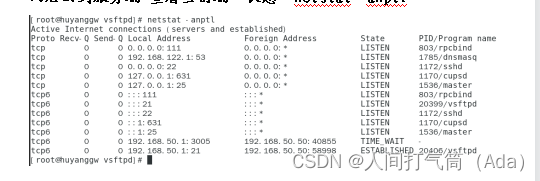
用户验证FTP实验
用户FTP实验 目录 匿名用户验证: 本地用户验证: 本地用户访问控制: 匿名用户验证: 例:(前提配置,防火墙关闭,yum安装,同模式vmware11) 现有一台计算机huy…...

App 软件开发《单选4》试卷答案及解析
App 软件开发《单选4》试卷答案及解析 注:本文章所有答案的解析来自 ChatGPT 的回答(给出正确答案让其解释原因),正确性请自行甄辨。 文章目录 App 软件开发《单选4》试卷答案及解析单选题(共计0分)1&#…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
