生成式模型的质量评估标准
Sample Quality Matrix
- 如何评价生成式模型的效果?
- IS
- FID
- sFID
- Precision & Recall
- Precison
- Recall
- 计算precision和recall
如何评价生成式模型的效果?
Quality: 真实性(逼真,狗咬有四条腿)
Diversity: 多样性(哈巴狗,金毛,吉娃娃,中华田园犬)
IS
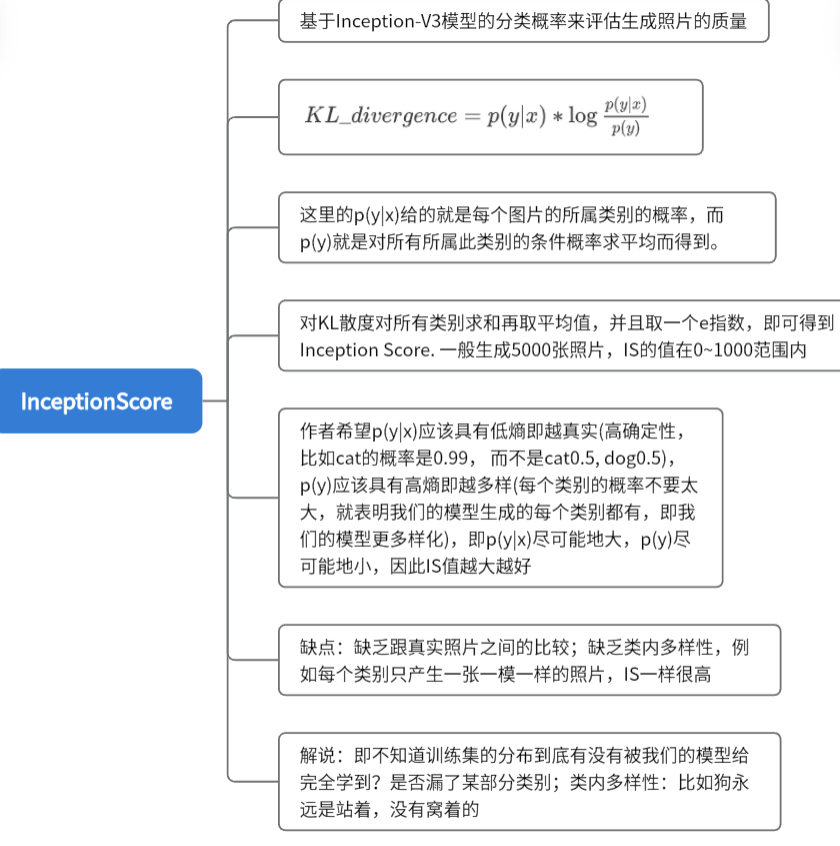
Inception Score
K L = p ( y ∣ x ) ∗ l o g p ( y ∣ x ) ) l o g ( p ( y ) KL = p(y|x)*log \frac{p(y|x))}{log(p(y)} KL=p(y∣x)∗loglog(p(y)p(y∣x))
Inception-V3是一个图像分类的模型,在imageNet上进行训练得到的预训练模型
p(y|x):即我们的模型生成的照片,它属于某个类别的概率
p(y):即边缘概率
#用代码实现IS
def calculate_inception_score(p_yx, eps=1E-16):# p_yx 即p(y|x)# calculate p(y)p_y = expand_dims(p_yx.mean(axis=0), 0)#kl divergence for each imagekl_d = p_yx * (log(p_yx + eps) - log(p_y + eps))# sum over classes sum_kl_d = kl_d.sum(axis=1)# average over images avg_kl_d = mean(sum_kl_d)# undo the logs is_score = exp(avg_kl_d)return is_score
FID
Frechlet Inception Distance(FID)
鉴于IS的缺点,就有了FID的出现,它是一个距离的量,即和真实的图片(训练集)的一个对比
FID也是用Inception-V3这个预训练好的图像分类模型,但它用的不是分类概率了,而是中间的一个feature vectors
即:把生成的照片和训练集中真实的照片同时送入到Inception-V3中,将二者经过Inception-V3模型得到的中间的特征向量拿出来,算出一个高斯分布的统计量,再去计算这两个分布之间的一个W2距离。
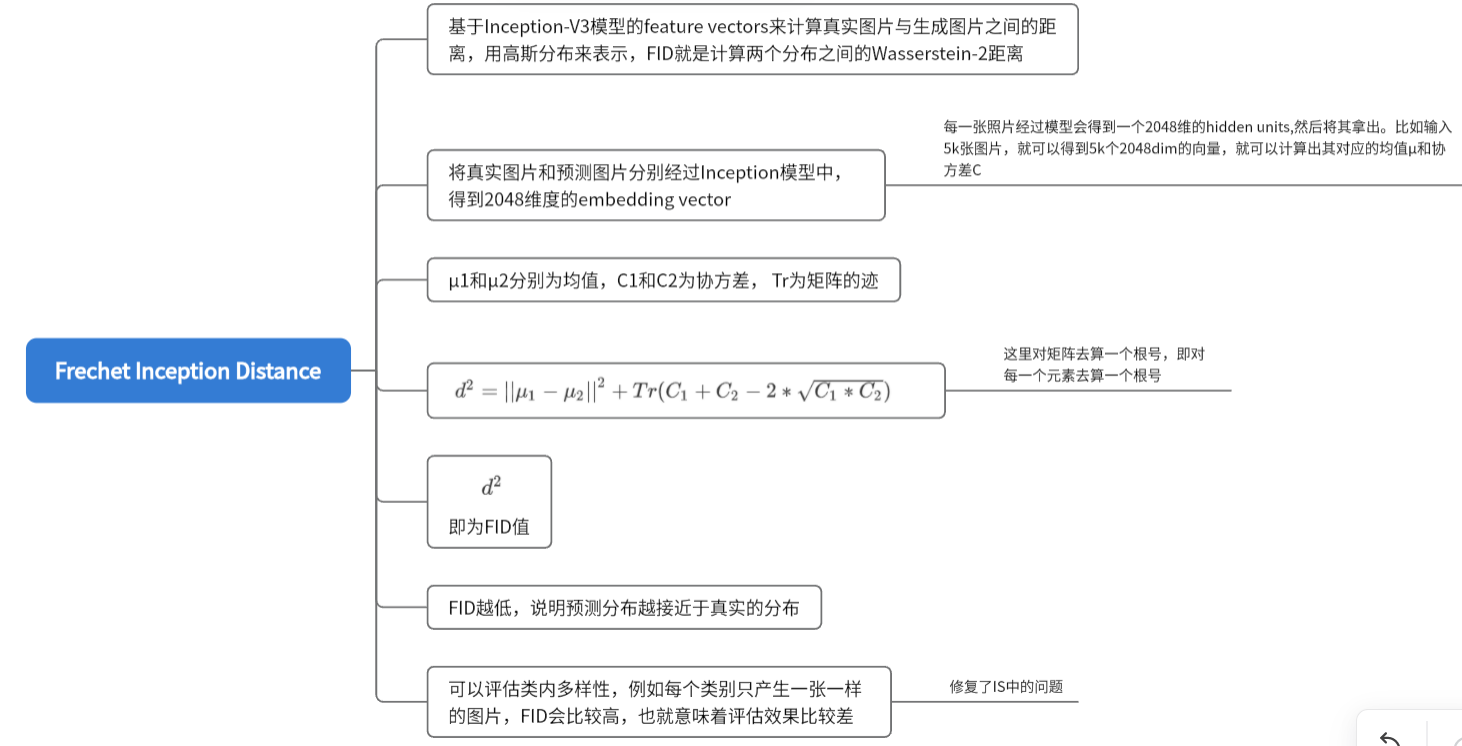
d 2 = ∣ ∣ μ 1 − μ 2 ∣ ∣ 2 + T r ( C 1 + C 2 − 2 C 1 ∗ C 2 ) d^2=||\mu_1-\mu_2||^2+Tr(C_1+C_2-2\sqrt{C_1*C_2}) d2=∣∣μ1−μ2∣∣2+Tr(C1+C2−2C1∗C2)
# 用代码实现FIDdef calculate_fid(act1, act2):'''act1:2048dim的隐变量,真实的图片送入Inception-V3中得到的act2:2048dim的隐变量,预测的图片送入Inception-V3中得到的'''# calculate mean and covariance statistics mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)# calculate sum squared difference between means ssdiff = numpy.sum((mu1 - mu2)**2.0)# calculate sqrt of product between cov covmean = sqrtm(sigma1.dot(sigma2))# check and correct imaginary numbers from sqrt if iscomplexobj(covmean):covmean = covmean.real# calculate score fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean)return fid
对于IS和FID,一般都是同时使用,而不是只使用其中一个
sFID
sliding Frechlet Inception Distance
和FID的不同就是用的隐变量不同,FID的隐变量是池化后的,sFID使用的是未经池化的隐变量
Precision & Recall
在生成式模型中,Precision(精确率)和Recall(召回率)通常用于评估生成的样本质量和多样性。以下是生成模型中计算Precision和Recall的常见方法:
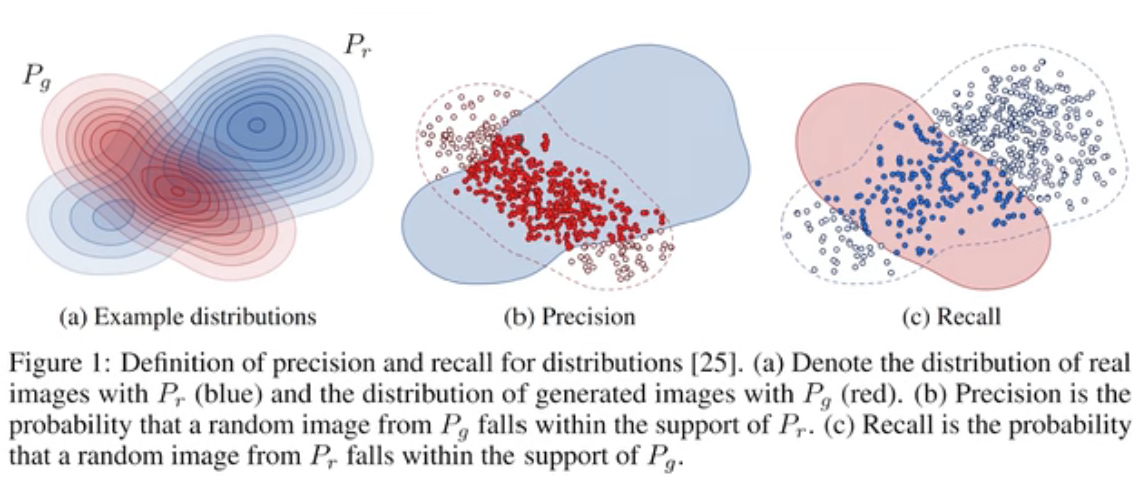
generated 分布用红色表示,real分布用蓝色表示
precision: 即红色的占蓝色分布的比例,即预测出来的样本占真实分布的比例
recall:即蓝色的点占红色的分布的比例,即真实的样本占预测分布的比例
理想情况是PR都大
Precison
Precision(精确率):Precision衡量生成的样本中有多少是真实样本的正确生成。它是通过计算生成样本中与真实样本匹配的比例来衡量的。一种常见的方法是使用K最近邻(K-nearest neighbors)来评估生成样本与真实样本之间的相似度。具体步骤如下:
对于每个生成样本,通过计算其与真实样本之间的距离(如欧氏距离或余弦相似度),找到其K个最近邻真实样本。
计算这K个最近邻中有多少真实样本,即与生成样本匹配的数量。
最后,将匹配数量除以生成样本的总数,得到Precision。
Recall
Recall(召回率):Recall衡量生成样本中成功覆盖真实样本的能力。它是通过计算真实样本中与生成样本匹配的比例来衡量的。具体步骤如下:
对于每个真实样本,通过计算其与生成样本之间的距离,找到其K个最近邻生成样本。
计算这K个最近邻中有多少是真实样本,即与真实样本匹配的数量。
最后,将匹配数量除以真实样本的总数,得到Recall。
计算precision和recall
用的是中间特征,而不是原图片本身
先把样本表示为 N × D N \times D N×D, D D D表示特征的维度, N N N表示为样本的个数
参考样本为: N 1 × D N1 \times D N1×D , 生成样本为: N 2 × D N2\times D N2×D
用KNN的方法,求出每个样本的k近邻,具体做法为:
用manifold_radii来求出每个元素的k个近邻的距离,求出radius后,
交叉去验证real分布中属于generative的样本的个数,计算得到precision
验证generative分布中属于real的样本的个数,计算得到recall
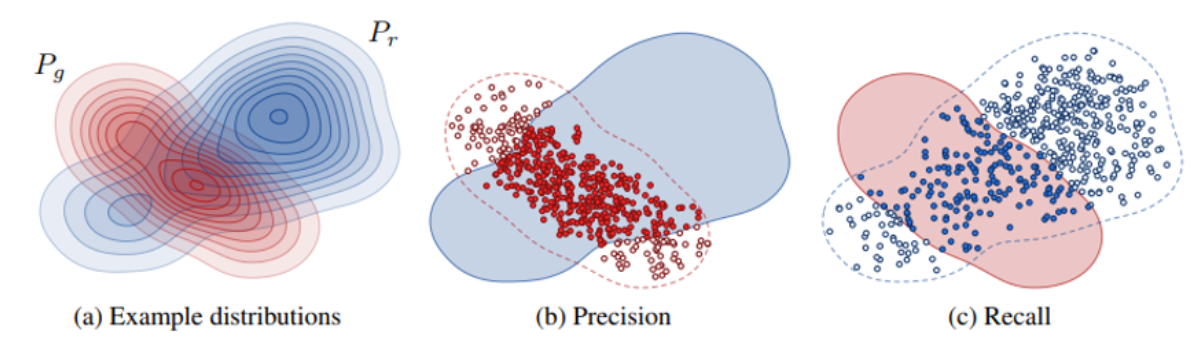
如何去获取real和generative的分布呢?
高效计算Precision和Recall。它比较两个批次的特征向量,根据流形半径判断它们是否在彼此的流形内。
将原始的N个图片 --> 表示为矩阵 N × D N\times D N×D
求得每个样本的 k 个近邻,即求得一个范围,相当于以每个样本为中心,画个圈,这样就可以表示出 real 的分布了,同理于generative分布,如下图所示。
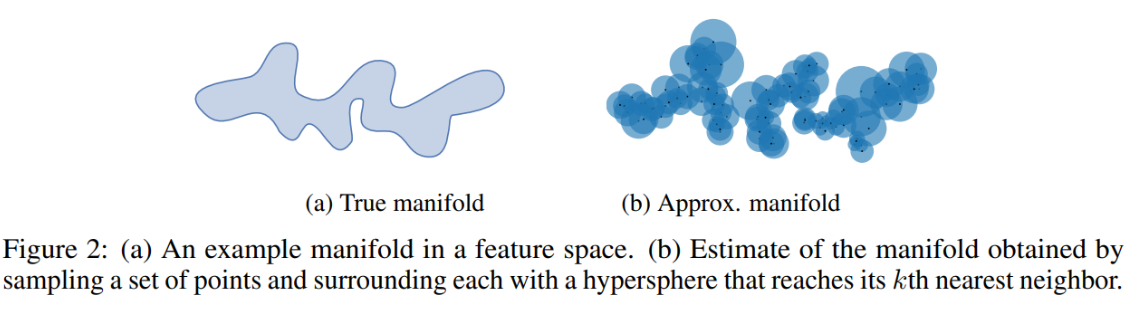
- Precision: 以real的每个样本为中心,画圈,计算real中的每个样本和generative中的每个样本的距离,如果在圈内,则说明是(b)中的红色实心部分, 红色实心部分占比与整个蓝色的部分
- Recall:以generative的每个样本为中心,画圈,计算generative中的每个样本和real中的每个样本的距离,如果在圈内,则说明是©中的蓝色实心部分,蓝色实心部分占比与整个红色部分
相关文章:

生成式模型的质量评估标准
Sample Quality Matrix 如何评价生成式模型的效果?ISFIDsFIDPrecision & RecallPrecisonRecall计算precision和recall 如何评价生成式模型的效果? Quality: 真实性(逼真,狗咬有四条腿) Diversity: 多样性&#x…...
pinpoint安装部署(相关博客合集)
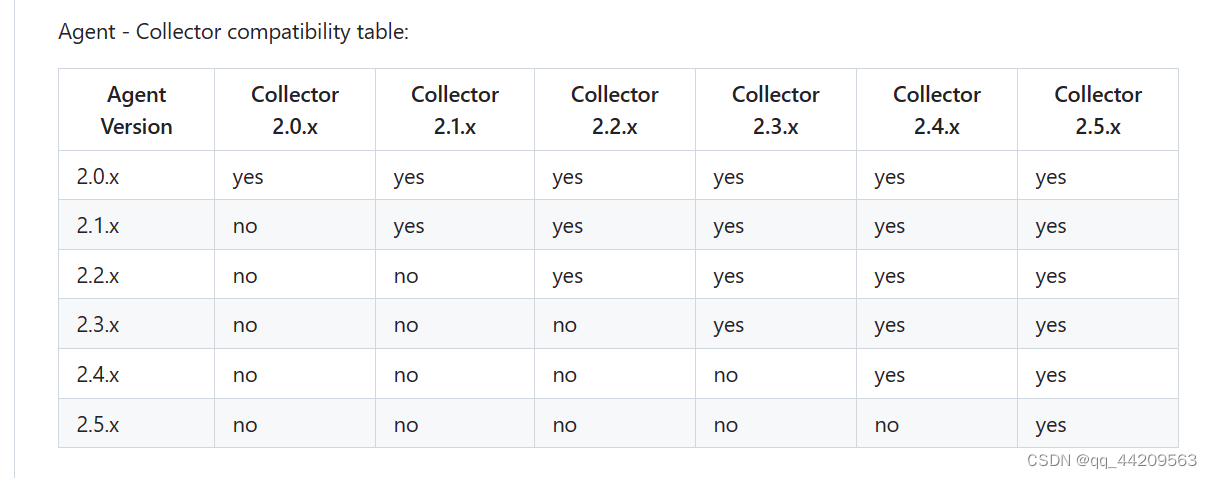
pinpoint安装部署 说明一、PinPoint介绍及工作原理1.1 确定部署的组件及服务 二、相关组件版本兼容情况2.1 确定版本 三、部署3.1 HBASE3.2 agent 说明 本博客写在搭建PinPoint之前,主要是用来记录查阅的相关博客资料,等到动手搭建完再更新实际部署操作…...
)
python-匿名函数(lambda函数)
匿名函数(lambda函数) 匿名函数(也称为lambda函数)是一种在代码中定义临时函数的方式,它没有明确的函数名称。匿名函数通常用于需要简短、一次性的函数定义,特别是在处理函数作为参数传递或函数返回的情况…...

JS逆向常见情况
分类:JS压缩混淆加密 与 URL/API参数的加密 代码压缩:去除不必要的空格换行等内容,使源码变成几行,大大降低可读性并提升网站加载速度 代码混淆:使用变量替换、字符串阵列化、控制流平坦化、多态变异、僵尸函数…...

利用matlab对滤波器频率特性分析
【设计目标】对双二阶环路滤波器进行时频域分析和处理的基本方法 【设计工具】MATLAB【设计要求】 1)分析典型的双二阶环路滤波器电路:低通、高通、带通、带阻 2)理论分析各滤波电路的系统函数 3)利用Matlab分析各滤波电路的系统函数的频率特性(幅频、相频)、零极点分…...
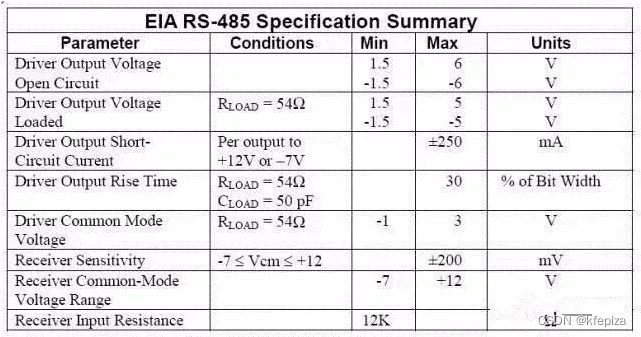
对比 RS232,RS422,RS485
对比 RS232,RS422,RS485 首先, 串口、UART口、COM口、RJ45网口、USB口是指的物理接口形式(硬件)。TTL、RS-232、RS-485、RS-422是指的电平标准(电信号)。 RS232,RS422,RS485 对比表格 通信标准RS-232RS-422RS-485工作方式单端差分差分通信线数量4 地线52 地线3节…...
python使用requests+excel进行接口自动化测试(建议收藏)
前言 在当今的互联网时代中,接口自动化测试越来越成为软件测试的重要组成部分。Python是一种简单易学,高效且可扩展的语言,自然而然地成为了开发人员的首选开发语言。而requests和xlwt这两个常用的Python标准库,能够帮助我们轻松…...

华为OD机试真题 Java 实现【食堂供餐】【2023 B卷 考生抽中题】,附详细解题思路
一、题目描述 某公司员工食堂以盒饭的方式供餐。 为将员工取餐排队时间降为0,食堂的供餐速度必须要足够快。 现在需要根据以往员工取餐的统计信息,计算出一个刚好能达到排队时间为0的最低供餐速度。 即,食堂在每个单位时间内必须至少做出多少份盒饭才能满足要求。 二、…...

一分钟学一个 Linux 命令 - cd
前言 大家好,我是 god23bin。欢迎来到这个系列,每天只需一分钟,记住一个 Linux 命令不成问题。今天让我们从 cd 命令开始,掌握在 Linux 系统中切换目录的技巧。 什么是 cd 命令? cd 命令来自这么一个词语࿰…...
常用命令汇总)
vi(vim)常用命令汇总
vim ~/.vimrc vim.vimrc 配置 set nobackup set cursorline #当前行 set cc100 #分屏线 set number set laststatus2 syntax on colorscheme delek 快速移动光标 w(e) 移动光标到下一个单词 b 移动光标到上一个单词 0 移动光标到本行最开头 ^ 移动光标到本行最开头的字符…...
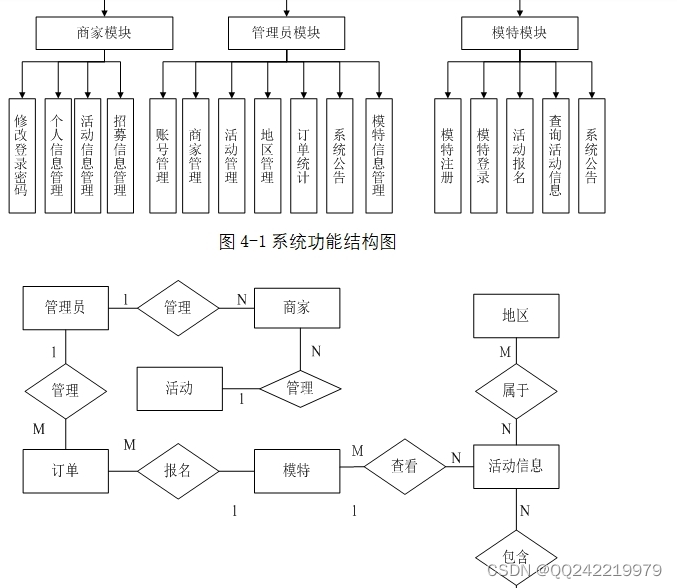
模特信息管理系统的开发与实现(ASP.NET,SQLServer)
需求分析 模特信息管理系统主要给商家和模特用户提供服务,系统分为前台和后台两部分。 本研究课题重点主要包括:活动管理,商家管理,模特管理,系统公告管理和活动报名管理。 活动管理模块主要实现活动更新、活动添加、活…...

文件上传漏洞
<1>概述 漏洞产生原因:服务端代码未对客户端上传的文件进行严格的验证和过滤,就容易造成可以上传任意文件的情况。 <2>文件上传绕过 (1)js检测绕过 1.删除js中检测文件的代码; 2.上传的文件改为允许的后缀绕过js检测后再抓包…...

前端还是后端,该怎么选择
在计算机科学领域,前端和后端是两个常见的方向,它们各自拥有独特的特点和职责。本文将对前端和后端进行比较,并总结哪些人适合前端,哪些人适合后端。 一、前端 前端开发主要涉及构建用户界面,处理用户交互和用户体验…...

【Python】Python系列教程-- Python3 循环语句(十七)
文章目录 前言while 循环无限循环while 循环使用 else 语句简单语句组for 语句for...elserange() 函数break 和 continue 语句及循环中的 else 子句pass 语句 前言 往期回顾: Python系列教程–Python3介绍(一)Python系列教程–Python3 环境…...

chatgpt赋能python:Python如何变为列表
Python如何变为列表 Python是一种高级编程语言,用于快速、轻松地编写软件。它的语法简洁、易于学习,可以用于各种领域,包括Web开发、机器学习和数据科学等。其中,列表是Python的一种基本数据类型,它用于存储一系列相关…...
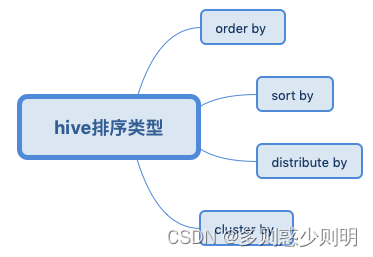
高频面试八股文用法篇(二) hive中几种排序类型区别
目录 排序函数 1、order by 2、sort by 3、distribute by 4、cluster by 总结 排序类型 1、order by order by是与关系型数据库的用法是一样的。select * from emp order by empno desc; 针对全局数据进行排序,所以最终只会有1个reduce,因…...
linuxOPS基础_linux umask
1、什么是umask umask表示创建文件时的默认权限(即创建文件时不需要设置而天生的权限) 例如: root用户下,touch a ,文件a的默认权限是644 普通用户下,touch b ,文件b的默认权限是664 644和…...

K8s基础核心
Kubernetes (K8s) 是一个用于自动化部署、扩展和管理容器化应用程序的开源平台。下面是 Kubernetes 的一些核心概念: Pod(容器组):Pod 是 Kubernetes 中最小的可调度和管理的单元 ,它可以包含一个或多个相关的容器。这…...

Web开发中的图片管理:策略与实践
前言 在Web开发中,图像是无法忽视的重要组成部分。然而,随着图片数量的增加和高清图像的普及,图片管理变得越来越复杂。在这篇文章中,我们将详细探讨Web开发中的图片管理策略和实践,包括图片优化、存储、分发和加载策…...

SNK施努卡 - 机器视食品检测 食品中视觉检查的作用是什么?
随着工业4.0时代的到来,机器视觉在工业领域的应用场景越来越广泛。在食品工业领域中,机器视觉的应用大大提高了食品生产企业的生产效率,有效的保证了产品品质的水准。 在智能工厂中,机器视觉系统能够实时监控生产工况。机器视觉系…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
