【1130. 叶值的最小代价生成树】
来源:力扣(LeetCode)
描述:
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有 0 个或是 2 个子节点。
- 数组
arr中的值与树的中序遍历中每个叶节点的值一一对应。 - 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
如果一个节点有 0 个子节点,那么该节点为叶节点。
示例 1:
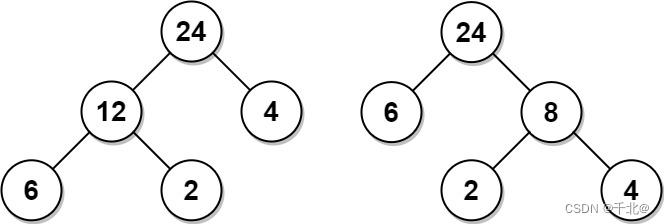
输入:arr = [6,2,4]
输出:32
解释:有两种可能的树,第一种的非叶节点的总和为 36 ,第二种非叶节点的总和为 32 。
示例 2:
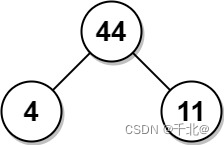
输入:arr = [4,11]
输出:44
提示:
- 2 <= arr.length <= 40
- 1 <= arr[i] <= 15
- 答案保证是一个 32 位带符号整数,即小于 231。
方法一:动态规划
已知数组 arr 与二叉树的中序遍历的所有叶子节点对应,并且二叉树的每个节点都有 0 个节点或 2 个节点。考虑数组 arr 可以生成的所有二叉树,我们可以将 arr 切分成任意两个非空子数组,分别对应左子树和右子树,然后递归地对两个非空子树组执行相同的操作,直到子数组大小等于 1,即叶子节点,那么一种切分方案对应一个合法的二叉树。
使用 dp[i][j] 表示子数组 [i, j] (i ≤ j) 对应的子树所有非叶子节点的最小总和,那么 dp[i][j] 可以通过切分子树求得,状态转移方程如下:

其中 mik 表示子数组 [i,k] 的最大值,可以预先计算并保存下来。
代码:
class Solution {
public:int mctFromLeafValues(vector<int>& arr) {int n = arr.size();vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 4)), mval(n, vector<int>(n));for (int j = 0; j < n; j++) {mval[j][j] = arr[j];dp[j][j] = 0;for (int i = j - 1; i >= 0; i--) {mval[i][j] = max(arr[i], mval[i + 1][j]);for (int k = i; k < j; k++) {dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + mval[i][k] * mval[k + 1][j]);}}}return dp[0][n - 1];}
};
执行用时:4 ms, 在所有 C++ 提交中击败了77.21%的用户
内存消耗:9 MB, 在所有 C++ 提交中击败了25.58%的用户
复杂度分析
时间复杂度:O(n3),其中 n 是数组 arr 的长度。三重循环需要 O(n3) 的空间。
空间复杂度:O(n2)。保存 dp 和 mval 需要 O(n2) 的空间。
方法二:单调栈
方法一的思路是自上而下构建二叉树,这里我们可以尝试自下而上构建二叉树:
- 选择 arr 两个相邻的值,即两个节点,将它们作为一个新节点的左子节点和右子节点;
- 将这个新节点在数组 arr 替代这两个节点;
- 如果 arr 剩余的元素数目大于 1,执行步骤 1,否则终止,那么剩余的节点就是构建的二叉树的根节点。
问题可以转化为:给定一个数组 arr,不断地合并相邻的数,合并代价为两个数的乘积,合并之后的数为两个数的最大值,直到数组只剩一个数,求最小合并代价和。
假设一个数 arr[i] (0 < i < n − 1),满足 arr[i−1] ≥ arr[i] 且 arr[i] ≤ arr[i+1],如果 arr[i−1] ≤ arr[i+1],那么优先将 arr[i] 与 arr[i−1] 合并是最优的,反之如果 arr[i−1] > arr[i+1],那么优先将 arr[i] 与 arr[i+1] 合并是最优的。
按照这种思路,套用单调栈算法(栈元素从底到顶是严格递减的),我们遍历数组 arr,记当前遍历的值为 x。
如果栈非空且栈顶元素小于等于 x,那么说明栈顶元素(类似于 arr[i])是符合前面所说的最优合并的条件,将栈顶元素 y 出栈:
- 如果栈空或栈顶元素大于 x,那么将 y 与 x 合并,合并代价为 x × y,合并之后的值为 x;
- 否则将 y 与栈顶元素合并,合并代价为 y 与栈顶元素的乘积,合并之后的值为栈顶元素。
重复以上过程直到栈空或栈顶元素大于 x,然后将 x 入栈。
经过以上合并过程后,栈中的元素从底到顶是严格递减的,因此可以不断地将栈顶的两个元素出栈,合并,再入栈,直到栈元素数目小于 2。返回最终合并代价和即可。
代码:
class Solution {
public:int mctFromLeafValues(vector<int>& arr) {int res = 0;stack<int> stk;for (int x : arr) {while (!stk.empty() && stk.top() <= x) {int y = stk.top();stk.pop();if (stk.empty() || stk.top() > x) {res += y * x;} else {res += stk.top() * y;}}stk.push(x);}while (stk.size() >= 2) {int x = stk.top();stk.pop();res += stk.top() * x;}return res;}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:8.1 MB, 在所有 C++ 提交中击败了76.28%的用户
复杂度分析
时间复杂度:O(n),其中 n 为数组 arr 的长度。每次循环都有入栈或出栈操作,总次数不超过 2 × n,因此时间复杂度为 O(n)。
空间复杂度:O(n)。栈 stk 需要 O(n) 的空间。
author:LeetCode-Solution
相关文章:

【1130. 叶值的最小代价生成树】
来源:力扣(LeetCode) 描述: 给你一个正整数数组 arr,考虑所有满足以下条件的二叉树: 每个节点都有 0 个或是 2 个子节点。数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。每个非叶节点的值等于…...

Linux各个目录的全称及含义
/ 根目录,包含整个文件系统的根节点。 /bin : Binary Directory 二进制文件目录,包含一些基本的可执行程序。 /boot : Boot Directory 包含启动系统所需的文件,如内核和引导程序。 /dev : Device Directory 设备文件目录,…...
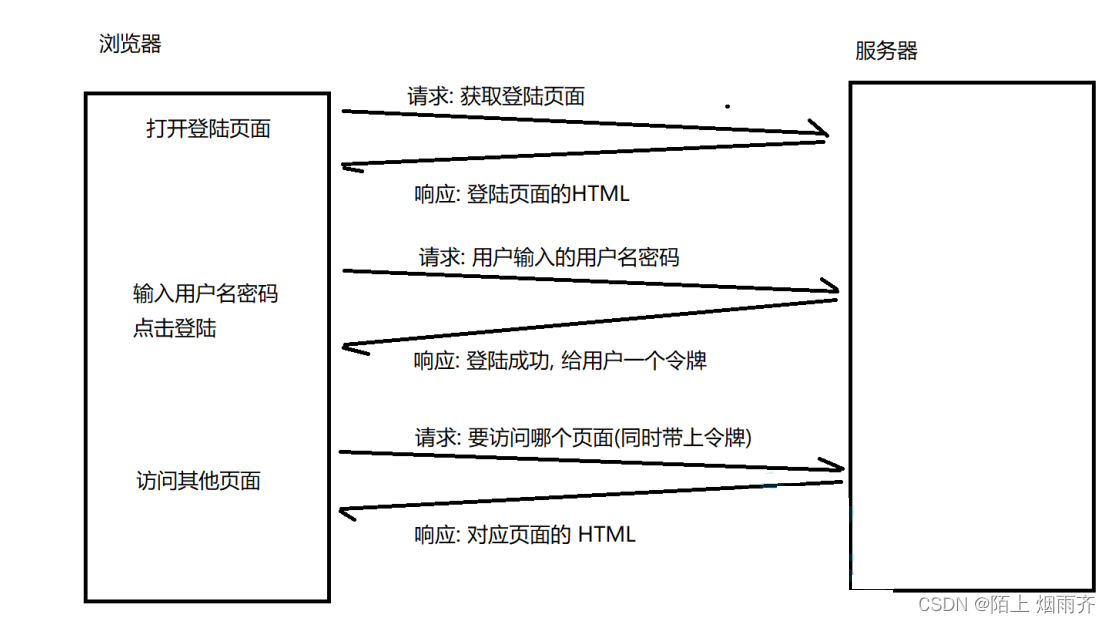
Cookie和Session原理详解
目录 前言 Cookie Session 会话机制 Cookie和Session的区别 Servlet中对Session和Cookie的封装 代码实例:实现用户登录 约定前后端交互的接口 前端页面: 后端实现 login index 总结 前言 在web的发展史中,我们知道浏览器和服务…...

小程序自动化测试
背景 近期团队打算做一个小程序自动化测试的工具,期望能够做到业务人员操作一遍小程序后,自动还原之前的操作路径,并且捕获操作过程中发生的异常,以此来判断这次发布是否会影响小程序的基础功能。 上述描述看似简单,…...

【linux系统操作】 - 技术一览
文章目录 1. 用户管理2. 文件管理3. 文件系统4. 字符处理5. 网络管理6. 进程管理7. 软件安装8. vi和vim编辑器9. 正则表达式 1. 用户管理 1.用户和用户组 2.账号管理 新增和删除用户、组;检查用户信息切换用户信息、用其他用户身份执行例行任务管理 : 周期性执行任…...

yield和sleep 区别
yield和sleep对比 sleepyieldsleep会导致当前线程暂停指定的时间,没有CPU时间片的消耗。yield只是对CPU调度器的一个提示,如果CPU调度器没有忽略这个提示,它会导致线程上下文的切换。sleep会使线程短暂block,会在给定的时间内释放…...

Redis 注册服务,自动启动
通常情况下我们可以通过 redis-server.exe 和配置文件启动redis服务 : 命令: redis-server.exe redis.windows.conf 另外开启一个命令行窗口 redis-cli.exe 即可做一些简单的操作命令行 但如果我们关闭控制台,那么Redis服务也跟随着一起关闭了&#x…...

华为OD机试真题 Java 实现【字符统计】【2023 B卷 100分】
一、题目描述 输入一个只包含小写英文字母和数字的字符串,按照不同字符统计个数由多到少输出统计结果,如果统计的个数相同,则按照ASCII码由小到大排序输出。 数据范围:字符串长度满足 1≤len(str)≤1000 。 二、输入描述 一个只包含小写英文字母和数字的字符串。 三、…...

ASP.NET Core MVC 从入门到精通之自动映射(一)
随着技术的发展,ASP.NET Core MVC也推出了好长时间,经过不断的版本更新迭代,已经越来越完善,本系列文章主要讲解ASP.NET Core MVC开发B/S系统过程中所涉及到的相关内容,适用于初学者,在校毕业生,…...

4. WebGPU 存储缓冲区 (WebGPU Storage Buffers)
这篇文章是关于存储缓冲区的,我们从上一篇文章暂停的地方继续。 存储缓冲区在许多方面类似于统一缓冲区。如果我们所做的只是将 JavaScript 中的 UNIFORM 更改为 STORAGE 并将 WGSL 中的 var 更改为 var<storage, read> ,那么上一页中的示例就可以…...

ChatGPT 插件功能深度解析:acquire、scholarai、form
引言 在我们的日常工作中,插件扮演着重要的角色,它们可以帮助我们提高工作效率,简化复杂的任务。在这篇文章中,我将详细介绍三个非常实用的插件:acquire、scholarai和form。 1、acquire 插件详解 acquire插件是一个…...

【面试集锦 - 汽车电子 - ASPICE]
ASPICE ASPICE(Automotive Software Performance Improvement and Capability dEtermination)是一种针对汽车电子行业的软件过程评估和改进模型。它是一种国际标准,旨在帮助汽车制造商和供应商评估和改进其软件开发过程的能力,以…...

深入探索Vue.js响应式原理及其实现机制
导语:Vue.js的核心特性之一是其强大的响应式系统,它使得数据和视图能够自动保持同步。在本文中,我们将深入探索Vue.js的响应式原理及其实现机制,帮助您更好地理解Vue.js的工作方式。 数据劫持:Vue.js的响应式系统通过数…...

Spark SQL概述、数据帧与数据集
文章目录 一、准备工作1、准备数据文件2、启动Spark Shell 二、加载数据为Dataset1、读文件得数据集 三、给数据集添加元数据信息1、定义学生样例类2、导入隐式转换3、将数据集转换成学生数据集4、对学生数据集进行操作(1)显示数据集内容(2&a…...

c# cad 二次开发 类库 CAD表格的操作,给CAD添加一个表格
c# cad 二次开发 类库 CAD表格的操作,给CAD添加一个表格 using Autodesk.AutoCAD.ApplicationServices; using Autodesk.AutoCAD.Colors; using Autodesk.AutoCAD.DatabaseServices; using Autodesk.AutoCAD.EditorInput; using Autodesk.AutoCAD.Geometry; using A…...

单点登录的两种实现方式,分别有啥优缺点?
单点登录(Single Sign-On,简称SSO)是指在多个应用系统中,用户只需要登录一次,就可以访问所有已授权的系统资源的一种身份认证技术。SSO可以提升用户体验,减少用户密码管理工作量,并加强安全管理…...

opencv_c++学习(二十七)
一、单目相机模型 上图为针孔相机成像原理,蓝色坐标中的O即为镜头光心。成像原理与小孔成像相同。 单目相机映射关系如下: 将上式进行变换,就可以从三位空间映射到2维平面的公式。 相机的畸变公式如下: 二、模型投影函数 vo…...

探查chatGPT插件:Outschool,resume,webhooks
引言 在我们的日常工作和学习中,插件扮演着重要的角色。它们可以帮助我们提高效率,简化复杂的任务。在这篇文章中,我将介绍三个非常有用的插件:Outschool,resume,和webhooks,并通过具体的例子来…...
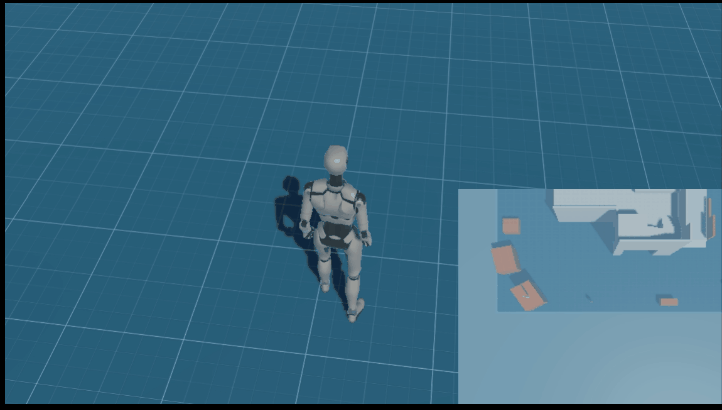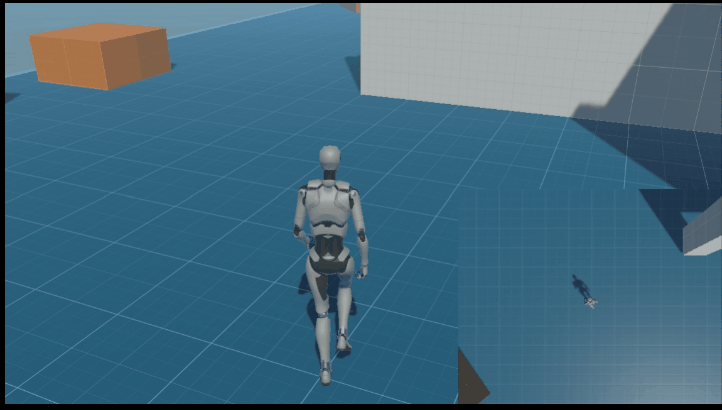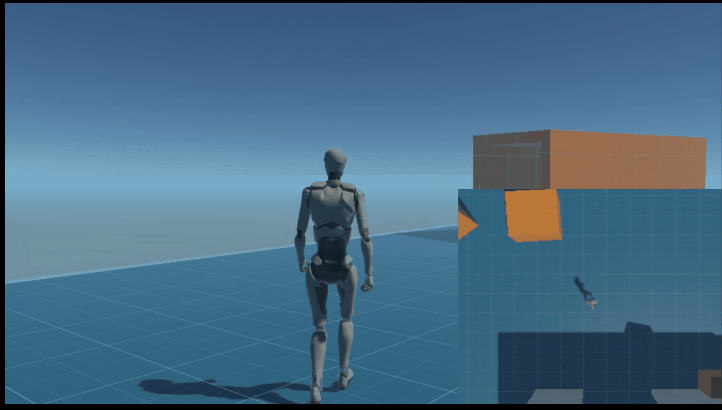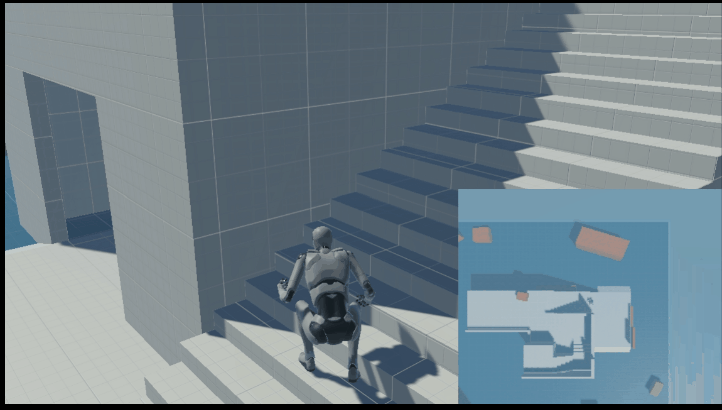
【学习笔记】Unity基础(七)【uGUI基础、利用render Texture实现小地图功能】
目录 一 Canvas1.1 三种Render Space渲染空间 screen1.2 canvas scaler画布缩放器1.3sprite1.4 sprite packer1.5 unity目录1.6 RuleTile Tilemap1.7 sprite packer1.8 sorting layer 二 rect transform2.1 pivot 中轴 中心点2.2 anchor 锚点2.3 uGUI源代码 三 EventSystem3.1 …...
yolov5配置错误记录
这里是直接没有找到数据集,说明是路径错误。经过设置yaml后, # Train/val/test sets as 1) dir: path/to/imgs, 2) file: path/to/imgs.txt, or 3) list: [path/to/imgs1, path/to/imgs2, ..] path: ../autodl-tmp/datasets/neu # dataset root dir tr…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
