华为OD机试真题 Java 实现【矩阵最大值】【2023 B卷 100分】,附详细解题思路

一、题目描述
给定一个仅包含0和1的N*N的二维矩阵,请计算二维矩阵的最大值。
计算规则如下:
1、每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行的值。矩阵各行值之和为矩阵的值。
2、允许通过向左或向右整体循环移动每行元素来改变各元素在行中的位置。
比如:
[0,1,0,0,1]向右整体循环移动1位变为[1,0,1,0,0],二进制数为10100,值为20。
[1,1,0,1,1]向右整体循环移动2位变为[1,1,1,1,0],二进制数为11110,值为30。
二、输入描述
1、第一行输入一个正整数,记录N的大小。
2、接下来的N行输入二维矩阵信息,行内元素逗号隔开。
三、输出描述
矩阵的最大值。
四、解题思路
本题的核心思路就是:
1、遍历整个二位矩阵,通过右移的方式,找到当前行的最大值;
2、通过substring拼接的方式实现右移;
详细的解题思路:
- 第一行输入一个数字N,表示N*N的二维矩阵的大小;
- 接下来的N行输入,N行输入二维矩阵信息,行内元素逗号隔开;
相关文章:

华为OD机试真题 Java 实现【矩阵最大值】【2023 B卷 100分】,附详细解题思路
一、题目描述 给定一个仅包含0和1的N*N的二维矩阵,请计算二维矩阵的最大值。 计算规则如下: 1、每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行的值。矩阵各行值之和为矩阵的值。 2、允许通过向左或向右整体循环移动每行元素来改变各元…...

ModuleNotFoundError: No module named ‘transformers_modules.chatglm-6b_v1‘的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
MMPretrain代码课
安装注意事项 训练时需要基于算法库源码进行开发,所以需要git clone mmpretrain仓库。如果只调用,则pip install 即可。 from mmpretrain import get_model, list_models,inference_model分别用于模型的获取、例举、推理 此时还没加载预训练权重 tor…...

Selenium自动化程序被检测为爬虫,怎么屏蔽和绕过
Selenium 操作被屏蔽 使用selenium自动化网页时,有一定的概率会被目标网站识别,一旦被检测到,目标网站会拦截该客户端做出的网页操作。 比如淘宝和大众点评的登录页,当手工打开浏览器,输入用户名和密码时,…...

Nvidia Jetson Orin:开发技巧
Jetson PXXX定义 P2180 -> Jetson TX1 P3310 -> Jetson TX2 P3489 -> Jetson TX2i P3448 -> Jetson Nano devkit P3448-0020 -> Jetson Nano production module P2888 -> Jetson Xavier P2888-0060 -> Jetson Xavier-8GB P3701 -> Jetson AGX Orin D…...

为什么需要 git 和 相关的小知识
为什么需要git和相关的小知识 先看一个实际需求,引出Git 问题: 公司五一活动计划 ● 先说一个最简单的情况,比如你做了公司五一活动计划书(如图) 解决方案: 版本管理工具(Git) 一句话: Git 是目前最流行的分布式版本控制软件 Git 是怎么来的? Git…...

(详解)vue中实现主题切换的三种方式
目录 一、背景 二、实现思路 方法1:定义全局的CSS变量 方法2:切换已定义好的css文件 方法3:切换顶级CSS类名 (需使用css处理器,如sass、less等) 一、背景 在我们开发中我们会遇到像是需要切换程序风格、主题切换啦这种应用场景。 参考大佬…...
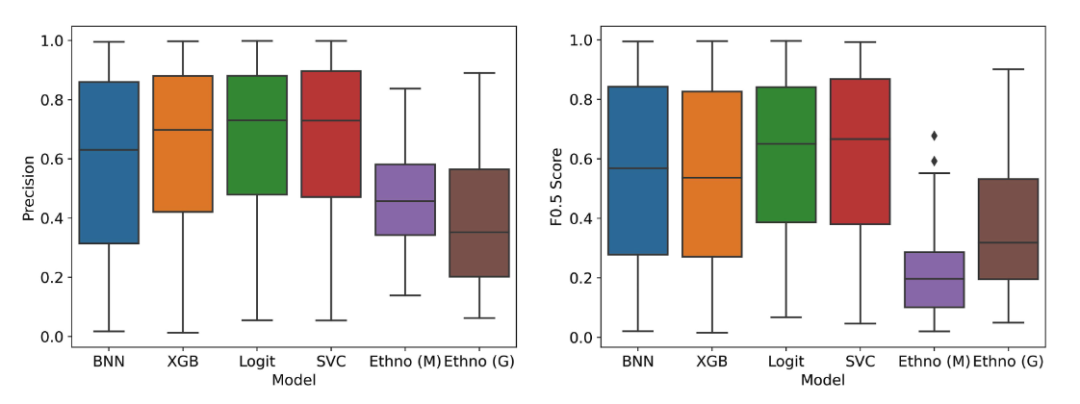
英国皇家植物园采用机器学习预测植物抗疟性,将准确率从 0.46 提升至 0.67
内容一览:疟疾是严重危害人类生命健康的重大传染病,研究人员一直在致力于寻找新的植物源性抗疟疾化合物,以研发相关药物。近期英国皇家植物园利用机器学习 算法 有效预测了植物抗疟性,该研究成果目前已发表在《Frontiers in Plant…...

基于Locust实现MQTT协议服务的压测脚本
一、背景简介 业务背景大概介绍一下,就是按照国标规定,车辆需要上传一些指定的数据到ZF的指定平台,同时车辆也会把数据传到企业云端服务上,于是乎就产生了一些性能需求。 目前我们只是先简单的进行了一个性能场景的测试…...

AURIX TC3XX Cached PFLASH与Non-Cached PFLASH的区别
Cached ? Non-Cached? 在阅读TC3XX的用户手册时,在内存映射表中,有两个segment都是Program Flash,而且大小都一样是3M,一个是segment 8 另一个是segment10 这难免让人产生疑惑,二者区别在哪? …...
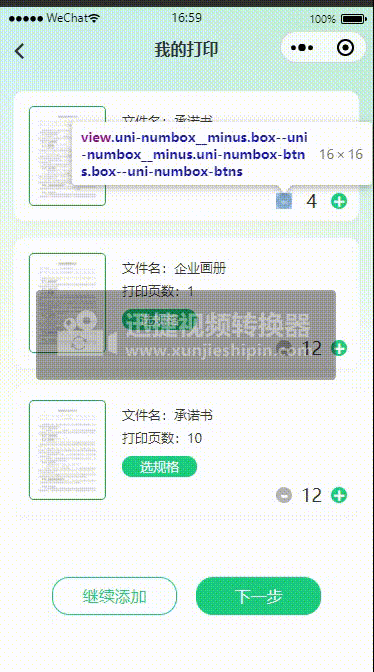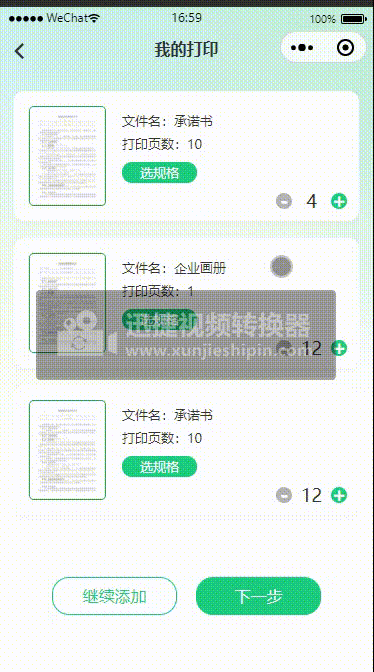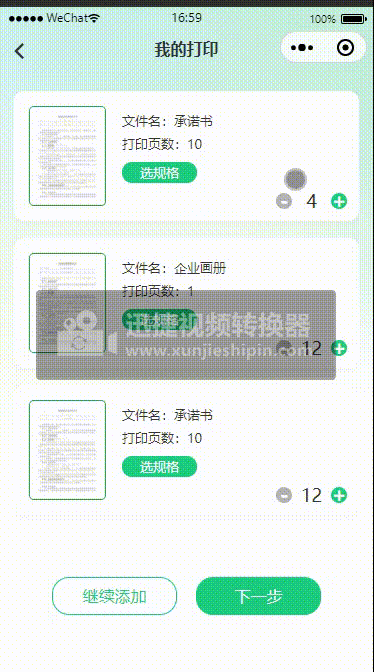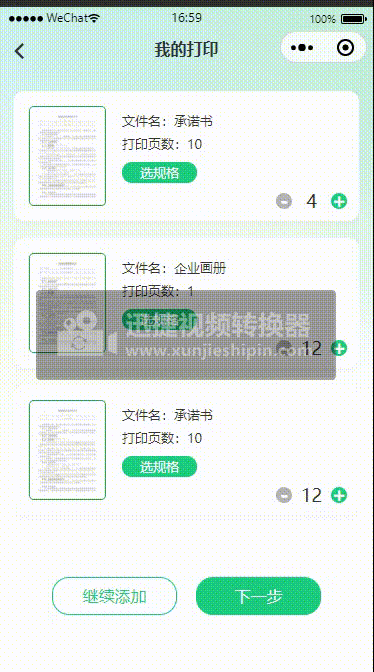
uniapp开发小程序-显示左滑删除效果
一、效果图: 二、代码实现: <template><view class"container"><view class"myorderList"><uni-swipe-action><uni-swipe-action-item class"swipe-action-item" :right-options"option…...

FPGA 的数字信号处理:Verilog 实现简单的 FIR 滤波器
该项目介绍了如何使用 Verilog 实现具有预生成系数的简单 FIR 滤波器。 绪论 不起眼的 FIR 滤波器是 FPGA 数字信号处理中最基本的模块之一,因此了解如何将具有给定抽头数及其相应系数值的基本模块组合在一起非常重要。因此,在这个关于 FPGA 上 DSP 基础…...

使用粒子群优化算法(PSO)辨识锂电池二阶RC模型参数(附MATLAB代码)
目录 一、原理部分 二、代码详解部分 三、结果及分析 一、原理部分 PSO算法由美国学者于 1995 年提出,因其算法简单、效果良好,而在很多领域得到了广泛应用。该算法的起源是模拟鸟群的觅食过程,形成一种群体智能搜索算法。 其核心是&#…...

如何利用地面控制点实现倾斜摄影三维模型数据的几何坐标变换和纠正?
如何利用地面控制点实现倾斜摄影三维模型数据的几何坐标变换和纠正? 倾斜摄影是一种在空中拍摄地表物体的技术,可以获得高分辨率、高精度的三维模型数据,广泛应用于城市规划、建筑设计、土地管理等领域。然而,由于航拍时无法避免姿…...

设计规则之里氏替换原则
tip: 作为程序员一定学习编程之道,一定要对代码的编写有追求,不能实现就完事了。我们应该让自己写的代码更加优雅,即使这会费时费力。 相关规则: 推荐:体系化学习Java(Java面试专题) 1.6大设…...

【叠高高】叠蛋糕游戏的微信小程序开发流程详解
记得小时候玩过的搭积木游戏吗,和叠高高游戏原理差不多的,与之类似的还有盖高楼游戏,就是看谁盖的(叠的)最高,这里讲一下比较基础的叠高高游戏小程序实现过程,对编程感兴趣的同学可以参考学习一…...

收集关键词的方法有哪些?(如何查找精准的行业流量关键词)
关键词的收集通常可以通过以下几种方法: 关键词收集方法 1.根据市场价值、搜索词竞争性和企业实际产品特征进行筛选:确定您的关键词列表之前,建议先进行市场分析,了解您的竞争对手、行业状况和目标受众等信息,以更好地了解所需的特…...

【GreenDao】RxQuery查询并修改GreenDao数据库,完成后更新UI
GreenDao是一个轻量级的ORM(对象关系映射)数据库,而RxJava是一个响应式编程库,可以帮助我们更轻松地处理异步事件。在 Android 应用程序中,您可以使用这两个库一起处理数据库查询和更新,并使用观察者模式来…...

Modifier ‘public‘ is redundant for interface methods错误
java中接口的方法默认是 public abstract 的 所以放心的删掉public即可,如果改为protected 或者 private还会报错 接口的方法及变量的默认修饰符 1.接口中每一个方法也是隐式抽象的,接口中的方法会被隐式的指定为 public abstract (只能是 public abst…...
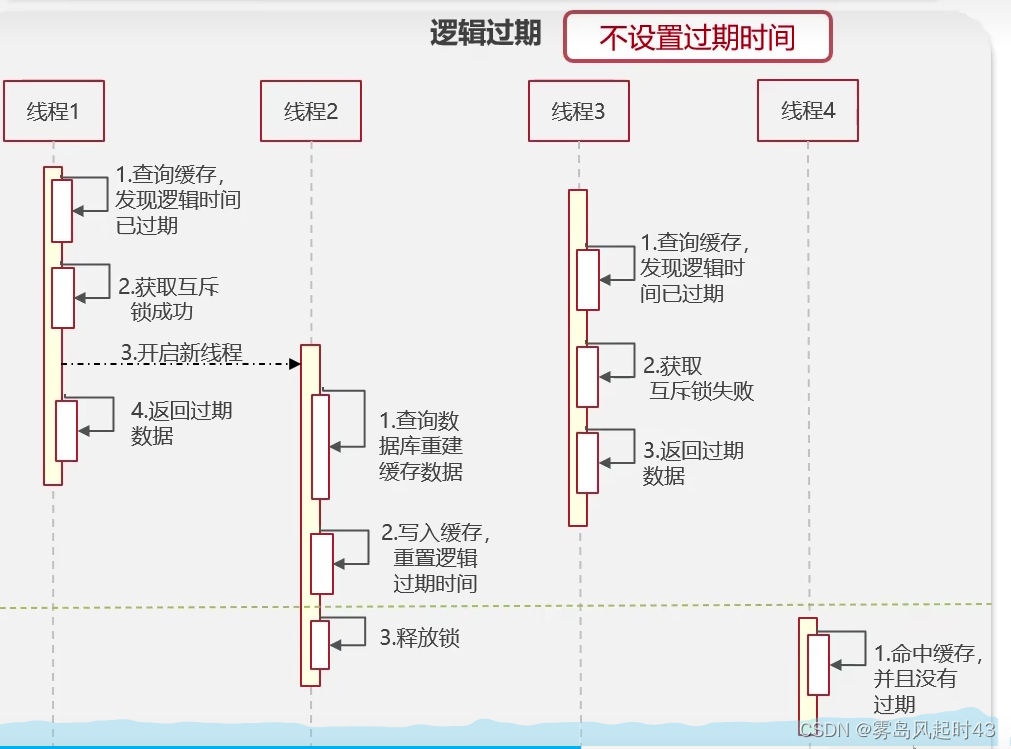
Redis缓存击穿及解决问题
缓存击穿的意思是对于设置了过期时间的key,缓存在某个时间点过期的时候,恰好这时间点对这个 Key有大量的并发请求过来,这些请求发现缓存过期- -般都会从后端DB加载数据并回设到缓存,这个时候大并发的请求可能会瞬间把DB压垮。 解决方案有两种…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
