数字图像处理实验报告
目录
实验二、图像在空间域上的处理方法
实验三、图像在频率域上的处理方法
实验二、图像在空间域上的处理方法
一、实验目的
- 了解图像亮(灰)度变换与空间滤波的意义和手段;
- 熟悉图像亮(灰)度变换与空间滤波的MATLAB函数和语法;
- 熟练掌握应用MATLAB软件编程进行图像亮(灰)度变换与空间滤波的方法;
- 完成数字图像的对比度增强和直方图均衡化,设计空间域平滑和锐化滤波器,掌握数字图像在空间域的基本处理方法。
二、实验环境
MATLAB 2014以上版本、Win 8\10\11 系统
三、实验原理
图像亮(灰)度变换与空间滤波属于在空间域内处理图像,是直接对图像的像素进行处理。有两种重要的空间域处理方法,即亮度(或灰度级)变换与空间滤波,后一种方法有时称为邻域处理或空间卷积。
图像亮(灰)度变换采用MATLAB工具箱中的亮度变换函数、直方图处理函数等函数及其相应的语法格式对实验一生成的图像进行处理;空间滤波采用MATLAB工具箱中的标准(线性和非线性)空间滤波器对图像进行空间滤波处理。
涉及函数:imread、size、figure、imshow、subplot、imadd、imsubtract 、rgb2gray、imhist、histeq、imnoise、medfilt2
四、实验内容
(1)新建一个m文件,从桌面示例图像文件夹中读取一张彩色图像,转换为灰度图,读取该图像尺寸,并在一个figure窗口同时展示,标题分别为(“原图”)及(“灰度图”)。
代码:
clc;clear;clear all;
RGB=imread('V.jpg'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
subplot(121);imshow(RGB),axis on,title("原图");
subplot(122);imshow(I),axis on,title("灰度图");
输出结果截图:
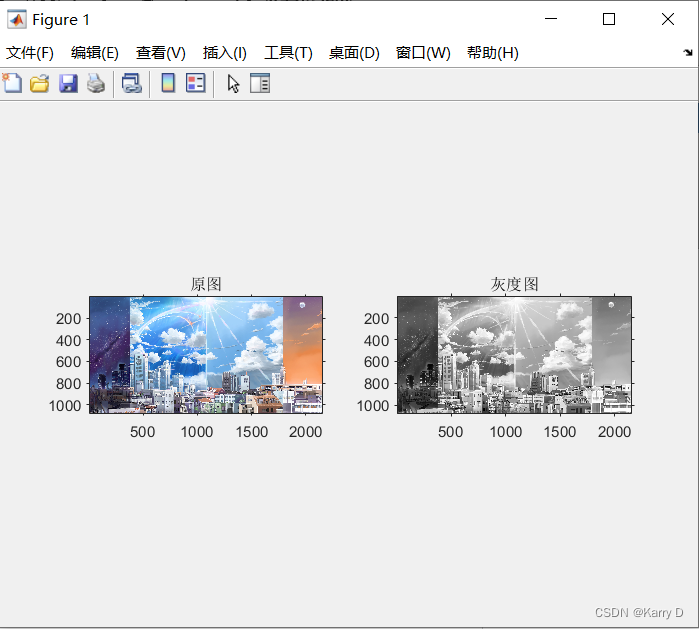
(2)读取一张彩色图像,转换为灰度图,使用imadd及imsubtract 分别对图像进行亮度增和减操作,数值为自己学号末位数×2,并在一个figure窗口同时展示,标题分别为“原图”、“灰度图”、“提亮结果”、“亮度降低结果”。点击右侧工作区中对应图像矩阵,观察亮度增减前后数值变化。
代码:
clc;clear;clear all;
RGB=imread('V.jpg'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
RGB2=imadd(RGB,20);
RGB3=imsubtract(RGB,20); %学号尾数为10
subplot(221);imshow(RGB),axis on,title("原图");
subplot(222);imshow(I),axis on,title("灰度图");
subplot(223);imshow(RGB2),axis on,title("提亮结果");
subplot(224);imshow(RGB3),axis on,title("亮度降低结果");
输出结果截图:

(3)读取两张彩色图像并转换为灰度图,使用imhist函数显示该图像的直方图,并使用histeq函数分别进行进行直方图均衡化处理。同一个figure窗口中输出,标题分别为“原图1”、“灰度图1”,“原图2”,“灰度图2”、“灰度直方图1”、“灰度直方图2”、“直方图均衡化1”、“直方图均衡化2”。
观察不同图像对应灰度直方图的特征有何差异,对比同一张图直方图均衡化前后的灰度分布差异。
代码:
clc;clear;clear all;
RGB=imread('V.jpg'); %图像读入
RGB1=imread('V1.jpg'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
I1=rgb2gray(RGB1); %把 RGB 图像转换成灰度图像
subplot(421);imshow(RGB),axis on,title("原图1");
subplot(422);imshow(I),axis on,title("灰度图1");
subplot(423);imshow(RGB1),axis on,title("原图2");
subplot(424);imshow(I1),axis on,title("灰度图2");
% 计算直方图
hist = imhist(I);
hist1 = imhist(I1);
% 对图像进行直方图均衡化处理
img_eq = histeq(I);
img_eq1 = histeq(I1);
subplot(425);bar(hist);axis on,title("灰度直方图1");
subplot(426);bar(hist1);axis on,title("灰度直方图2");
subplot(427);histeq(I),axis on,title("直方图均衡化1");
subplot(428);histeq(I1),axis on,title("直方图均衡化2");
输出结果截图:
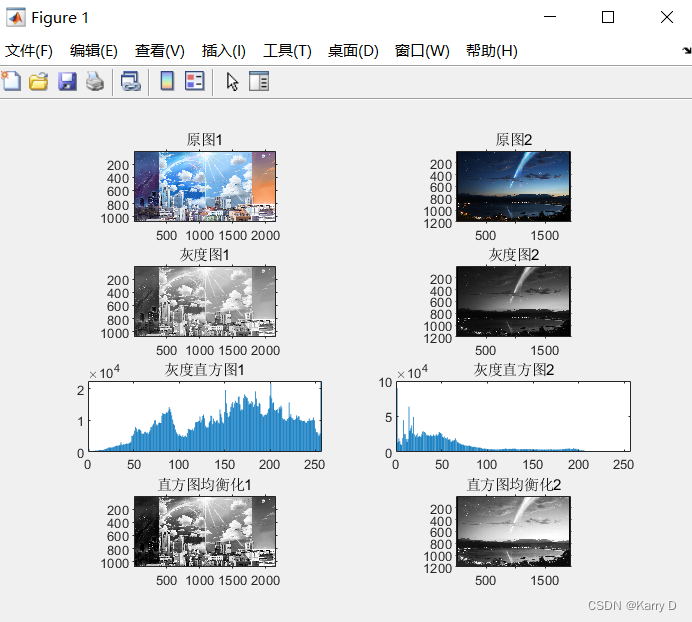
(4)读取一张彩色图像并转换为灰度图,使用imnoise添加椒盐噪声,例如I1=imnoise(I,’salt& pepper’,0.04); 分别使用3*3、5*5、7*7、9*9大小的模板进行中值滤波,在相同figure中输出,标题分别为“原图”、“添加椒盐噪声”、“x*x模板中值滤波”。
代码:
% 读取彩色图像并转换为灰度图
clc;clear;clear all;
RGB=imread('V.jpg'); %图像读入
I=rgb2gray(RGB); %把 RGB 图像转换成灰度图像
% 添加椒盐噪声
I_noise = imnoise(I, 'salt & pepper', 0.04);
% 使用不同大小的模板进行中值滤波
I_median3 = medfilt2(I_noise, [3 3]);
I_median5 = medfilt2(I_noise, [5 5]);
I_median7 = medfilt2(I_noise, [7 7]);
I_median9 = medfilt2(I_noise, [9 9]);
subplot(321);imshow(RGB),axis on,title("原图");
subplot(322);imshow(I_noise),axis on,title("添加椒盐噪声");
subplot(323);imshow(I_median3),axis on,title("3*3模板中值滤波");
subplot(324);imshow(I_median5),axis on,title("5*5模板中值滤波");
subplot(325);imshow(I_median7),axis on,title("7*7模板中值滤波");
subplot(326);imshow(I_median9),axis on,title("9*9模板中值滤波");
输出结果截图:

(5)读取一张彩色图像并转换为灰度图,利用im2bw函数转换为“二值图像”,分别使用sobel算子及Laplacian算子进行锐化,在相同figure中输出,标题分别为“原图”、“二值图像”、“sobel算子锐化”、“拉普拉斯算子锐化”。
提示:H=fspecail (‘soble’); J=filter2(H,I1);
代码:
% 读取一张彩色图像并转换为灰度图
clc;clear;clear all;
img = imread('V.jpg');
gray_img = rgb2gray(img);
% 利用im2bw函数转换为“二值图像”
bw_img = im2bw(gray_img);
% 使用sobel算子进行锐化
sobel_img = edge(bw_img, 'sobel');
% 使用Laplacian算子进行锐化
laplace_img = edge(bw_img, 'log');
% 在相同figure中输出结果
figure;
subplot(2,2,1);
imshow(img);
title('原图');
subplot(2,2,2);
imshow(gray_img);
title('灰度图');
subplot(2,2,3);
imshow(sobel_img);
title('Sobel算子锐化');
subplot(2,2,4);
imshow(laplace_img);
title('Laplacian算子锐化');
输出结果截图:

实验三、图像在频率域上的处理方法
一、实验目的
- 了解图像频域处理的意义和手段;
- 熟悉离散傅里叶变换的基本性质;
- 熟练掌握图像傅里叶变换的方法及应用;
- 通过实验了解二维频谱的分布特点;
- 通过本实验掌握利用MATLAB的工具箱实现数字图像的频域处理,构建各式常见频率域滤波器,并熟悉其特点与应用场景。
二、实验环境
MATLAB 2014以上版本、Win 8\10\11 系统
三、实验原理
图像的频率是图像在平面空间上的梯度,是表征图像中图像变化剧烈程度的指标。例如,大面积的海洋在图像中是一片图像变化缓慢的区域,对应的频率值很低;而地表属性变换剧烈的边缘区域在图像中则是一片图像变化剧烈的区域,对应的频率值较高。频域滤波增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其他空间中,然后利用该空间的特有性质方便地处理图像,最后再转换回原来的图像空间中,从而得到处理后的图像。图像的频率域处理图像处理中占有重要的地位,在图像的去噪、图像压缩、特征提取和图像识别方面发挥着重要的作用。
图像频率域采用MATLAB工具箱中的傅里叶变换函数、滤波函数等函数及其相应的语法格式图像进行处理;
在MATLAB 中,函数fft、fft2和fftn分别可以实现一维、二维和N维DFT 算法:而函数 ifft、ifft2 和 ifftn 则用来计算反 DFT。fftshift 函数可以把傅里叶操作(fft,fft2,fftn)得到的结果中的零频率成分移到矩阵的中心,这样有利于观察频谱;
涉及函数:imread、figure、imshow、subplot、rgb2gray、log、abs、fft、fft2、fftshift、ifft2
四、实验内容
(1)新建一个m文件,从桌面示例图像文件夹中读取一张彩色图像,转换为灰度图,利用傅里叶变换函数fft2与fftshift显示图像的傅里叶变换频谱图,并在一个figure窗口同时展示,标题分别为“原图”、“灰度图”、“变换频谱”。
代码:
clc;clear;clear all;
I=imread('V.jpg');
figure
subplot(311),imshow(I),title("原图像")
GrayI=rgb2gray(I);
subplot(312),imshow(GrayI),title('灰度图像')
fft2(GrayI);
S=fftshift(fft2(GrayI));
subplot(313),imshow(log(abs(S)),[]),title('频谱')
输出结果截图:
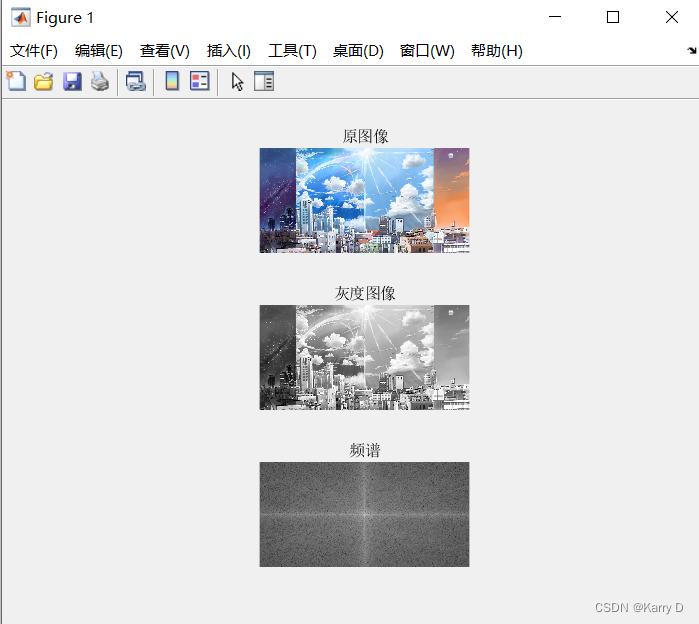
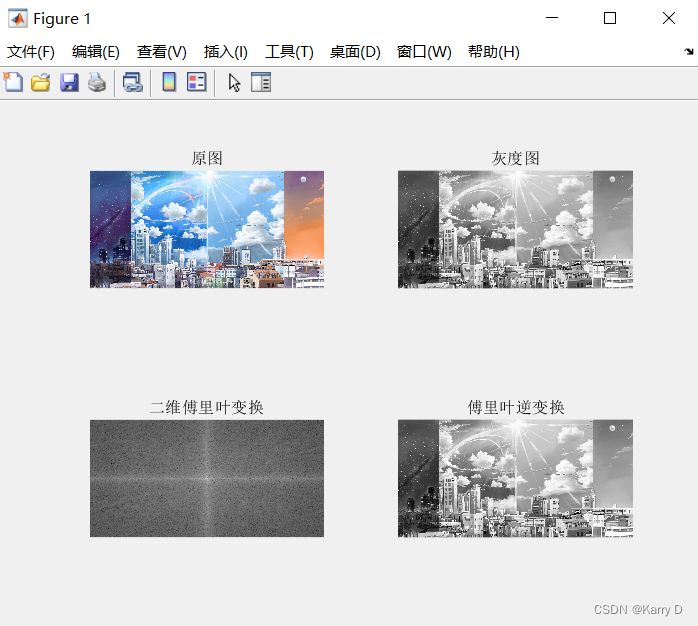
(2)读取一张彩色图像,转换为灰度图,使用fft2进行傅里叶变换,接着使用ifft2进行傅里叶逆变换,并在一个figure窗口同时展示,标题分别为“原图”、“灰度图”、“二维傅里叶变换”、“傅里叶逆变换”。观察变换前后图像,及对应图像矩阵是否与原图相同。
代码:
clc;clear;clear all;
% 读取彩色图像
rgb_img = imread('V.jpg');
% 转换为灰度图
gray_img = rgb2gray(rgb_img);
% 进行二维傅里叶变换
fft_img = fft2(gray_img);
% 进行傅里叶逆变换
ifft_img = ifft2(fft_img);
% 显示图像
figure;
subplot(2, 2, 1);
imshow(rgb_img);
title('原图');
subplot(2, 2, 2);
imshow(gray_img);
title('灰度图');
subplot(2, 2, 3);
imshow(abs(fftshift(fft_img)), []);
title('二维傅里叶变换');
subplot(2, 2, 4);
imshow(abs(ifft_img), []);
title('傅里叶逆变换');
输出结果截图:
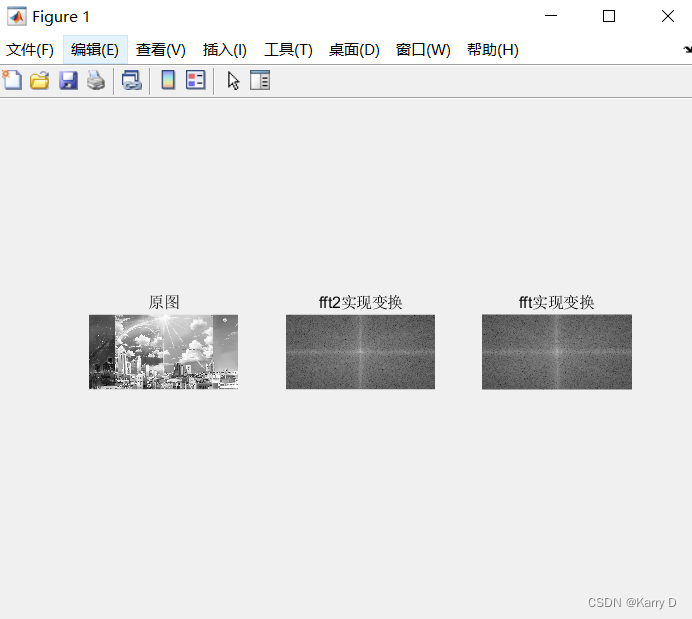
(3)读取一张彩色图像并转换为灰度图,接着对图像进行傅里叶正反变换,对比变换前后是否相同。同一个figure窗口中输出,标题分别为“原图”、“傅里叶变换”,“傅里叶反变换”。
代码:
clc;clear;clear all;
I=imread('V.jpg');
figure
subplot(311),imshow(I),title("原图像")
A=rgb2gray(I);
B=fft2(A);
C=fftshift(B);
subplot(312),imshow(log(abs(C)),[]),title('傅里叶变换')
D=ifft2(B);
subplot(313),imshow(uint8(abs(D))),title('傅里叶反变换')
输出结果截图:
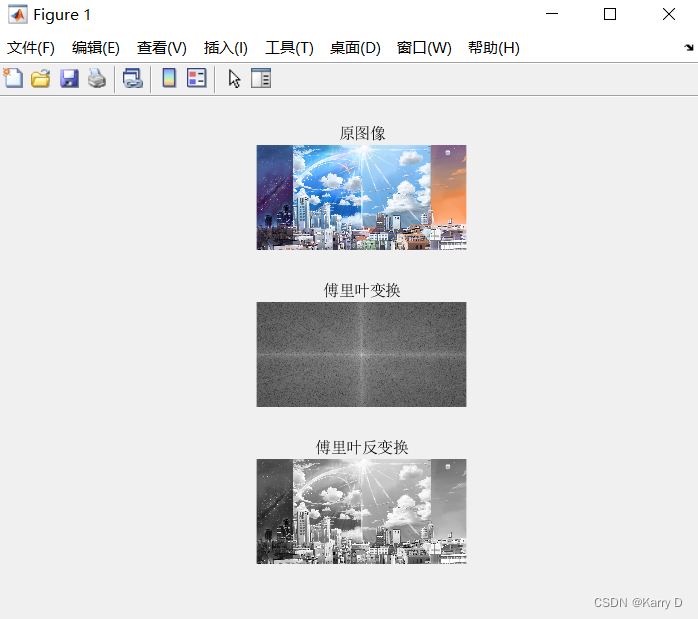
(4)读取一张彩色图像并转换为灰度图,使用fft函数及fft2函数验证二维离散傅里叶变换可分解为两个一维离散傅里叶变换(先行变换,后列变换)在相同figure中输出,标题分别为“原图”、“fft2实现变换”、“fft实现变换”。
代码:
clc;clear;clear all;
% 读取彩色图像并转换为灰度图
img = imread('V.jpg');
gray_img = rgb2gray(img);
% 在同一figure中输出原图
subplot(1,3,1);
imshow(gray_img);
title('原图');
% 使用fft2函数进行二维离散傅里叶变换
fft2_img = fft2(gray_img);
% 在同一figure中输出使用fft2函数实现的变换结果
subplot(1,3,2);
imshow(log(abs(fftshift(fft2_img))),[]);
title('fft2实现变换');
% 使用fft函数进行一维离散傅里叶变换(先行变换)
fft_row_img = fft(gray_img,[],1);
% 使用fft函数进行一维离散傅里叶变换(后列变换)
fft_col_img = fft(fft_row_img,[],2);
% 在同一figure中输出使用fft函数实现的变换结果
subplot(1,3,3);
imshow(log(abs(fftshift(fft_col_img))),[]);
title('fft实现变换');
输出结果截图:
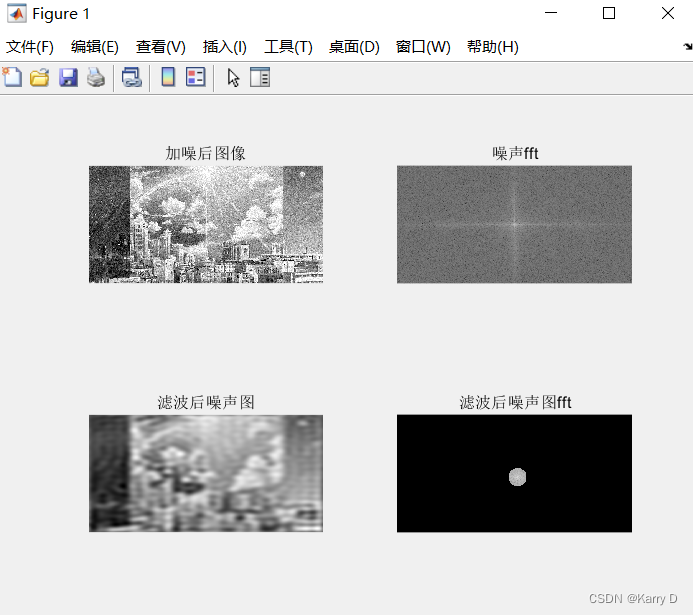
(5)读取一张彩色图像并转换为灰度图,使用imnoise函数加入高斯白噪声,绘制加噪后图像,使用fft函数绘制加噪后图像傅里叶频谱图。接着设计一个截止频率D0=M*10(其中M=学号末位数)的理想低通滤波器(ILPF)对图像进行滤波处理,绘制滤波后噪声图及滤波后的傅里叶频谱图。上述结果在同一figure中显示,标题分别为“加噪后图像”、“噪声fft”、“滤波后噪声图”、“滤波后噪声图fft”。
提示:
①对于大小为M*N的图像,频率点(u, v)与频率中心的距离为D(u, v),其表达式为:
![]()
②理想低通滤波器的产生公式为:
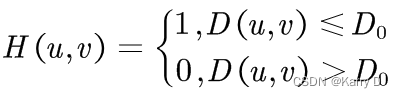
代码:
clc;clear;clear all;
% 读取彩色图像并转换为灰度图
rgb_img = imread('V.jpg');
gray_img = rgb2gray(rgb_img);
% 加入高斯白噪声
noisy_img = imnoise(gray_img, 'gaussian');
% 绘制加噪后图像
figure;
subplot(2,2,1);
imshow(noisy_img);
title('加噪后图像');
% 使用FFT函数绘制加噪后图像傅里叶频谱图
noisy_fft = fft2(noisy_img);
noisy_fft_shifted = fftshift(noisy_fft);
noisy_fft_mag = abs(noisy_fft_shifted);
subplot(2,2,2);
imshow(log(1+noisy_fft_mag), []);
title('噪声fft');
% 设计理想低通滤波器(ILPF)对图像进行滤波处理
M = 2; % 学号末位数是0(更换为2)
D0 = M*10;
[height, width] = size(noisy_img);
[x, y] = meshgrid(1:width, 1:height);
center_x = floor(width/2)+1;
center_y = floor(height/2)+1;
d = sqrt((x-center_x).^2 + (y-center_y).^2); % 欧几里得距离
H_ILPF = double(d<=D0); % 理想低通滤波器
% 对图像进行滤波处理
noisy_fft_filtered_shifted = noisy_fft_shifted .* H_ILPF;
noisy_filtered = real(ifft2(ifftshift(noisy_fft_filtered_shifted)));
% 绘制滤波后噪声图及滤波后的傅里叶频谱图
subplot(2,2,3);
imshow(noisy_filtered, []);
title('滤波后噪声图');
filtered_fft = fft2(noisy_filtered);
filtered_fft_shifted = fftshift(filtered_fft);
filtered_fft_mag = abs(filtered_fft_shifted);
subplot(2,2,4);
imshow(log(1+filtered_fft_mag), []);
title('滤波后噪声图fft');
输出结果截图:
相关文章:

数字图像处理实验报告
目录 实验二、图像在空间域上的处理方法 实验三、图像在频率域上的处理方法 实验二、图像在空间域上的处理方法 一、实验目的 了解图像亮(灰)度变换与空间滤波的意义和手段;熟悉图像亮(灰)度变换与空间滤波的MATLA…...

【C51】10-基础51单片机的小车项目(51完结)
10.1小车的安装 10.2电机模块的开发(L9110S) 接通 VCC , GND 模块电源指示灯亮, 以下资料来源官方,但是不对,根据下节课实际调试 IA1 输入高电平, IA1 输入低电平,【 OA1 OB1 】电…...

进程、线程、锁阶段总结汇总
目录 进程 线程 锁 由于进程线程和锁的方面比较陌生,并且繁杂,所以简单总结一下学习到的函数API 进程 子进程创建 fork(); 进程结束 exit(); 进程回收 wait(); 进程回收 waitpad(); //函数可以指定进程组中的任意子进程,可以设置特殊…...

Filters.jar图片转素描
链接:https://pan.baidu.com/s/1ATlC2l1I83TPYFomHiWuFg?pwd2vm5 提取码:2vm5...
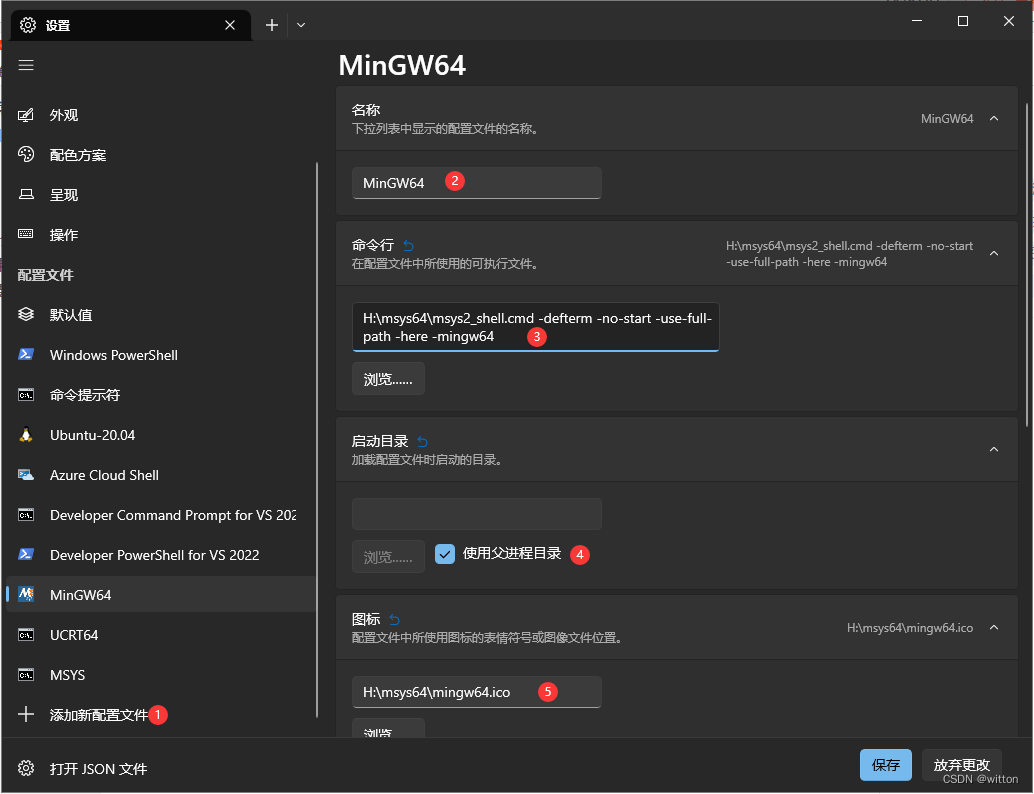
将MSYS2 MinGW集成到Windows终端
微软开发了一款Windows终端的开源软件,非常好用。安装后在Win7及以上系统会在右键菜单中添加一条“在终端中打开”的命令,非常方便。它默认配置了Windows命令行以及PowerShell,如果安装了Visual Studio 2022还会配置Visual Studio 2022的命令…...

SpringBoot项目使用slf4j的MDC日志打点功能
SpringBoot项目使用slf4j的MDC日志打点功能 物料准备: 1.自定义1个线程MDC打点工具类 2.配置logback打印MDC打点的traceId 3.配置webMVC使用MDC打点 4.配置ThreadPoolTaskExecutor使用MDC打点 5.配置HttpClient使用MDC打点 6.测试MDC日志打点效果 线程mdc打…...

宝塔修改默认端口后面板打不开
1、查看防火墙开启的端口,发现没有开启8888 [rootVM-12-12-centos ~]# firewall-cmd --list-ports 20/tcp 21/tcp 22/tcp 80/tcp 888/tcp 8081/tcp 39000-40000/tcp 8081/udp 2、防火墙开启8888端口 [rootVM-12-12-centos ~]# firewall-cmd --zonepublic --add-por…...

tinkerCAD案例:3.基本按钮
基本按钮 在本课中,您将学习制作具有圆柱形状的基本按钮。 说明 将圆柱体拖动到工作平面。 将其缩小到 2 毫米的高度。 提示: 您可以使用圆柱形状顶部的白点缩小圆柱体。 将其缩小到直径 16 毫米。 这将是按钮的主要形状。 现在我们可以创建允许将纽…...
客户线上反馈:从信息搜集到疑难 bug 排查全流程经验分享
写在前面:本文是我在前端团队的第三次分享,应该很少会有开发者写客户反馈处理流程以及 bug 排查的心得技巧,全文比较长,写了一个多星期大概1W多字(也是我曾经2年工作的总结),如果你有耐心阅读&a…...
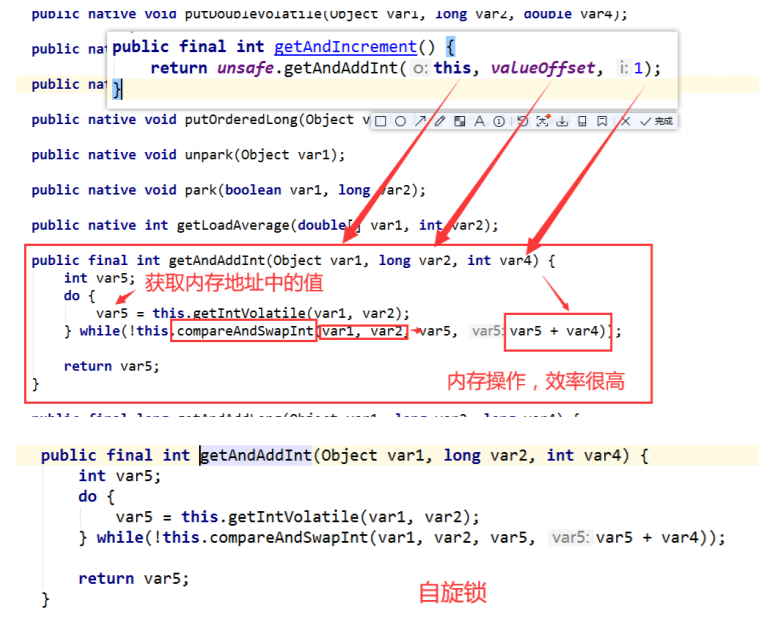
悲观锁、乐观锁、自旋锁
悲观锁、乐观锁、自旋锁 (1)乐观锁 乐观锁是一种乐观的思想,即认为读多写少,遇到并发的可能性低,每次拿数据时都认为别人不会修改,所以不会上锁,但是在更新的时候会判断一下在此期间别人有没有…...
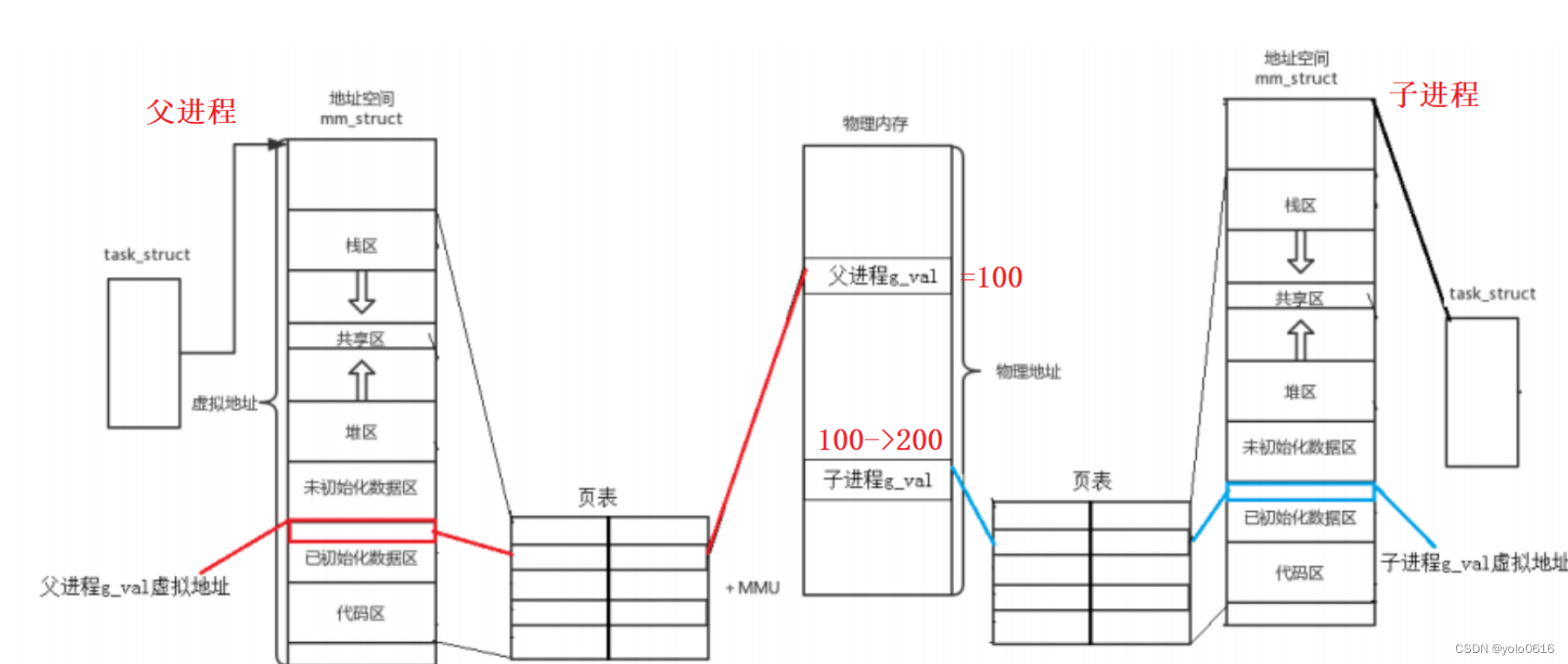
七、进程地址空间
一、环境变量 (一)概念 环境变量(environment variables):系统当中用做特殊用途的系统变量。 如:我们在编写C/C代码的时候,在链接的时候,从来不知道我们的所链接的动态静态库在哪里,但是照样可…...
浅谈智能微电网供电系统的谐波治理
摘要:智能微电网供电系统的特性容易引发谐波,而谐波导致电力损耗加大,降低供电质量。本文从谐波的产 生原因和危害做出详细阐述,并结合智能微电网提出了治 理谐波的方法和措施。 关键词:智能微电网;谐波危害…...
springboot项目的社区/博客系统
课前导读: 你学完一篇,你就多会一项技能,多多少少对你还是有点帮助的不是吗?~~~ 这是博主网页的url:优文共享社区 开发环境:JDK1.8,IDEA2021,MySQL5.7,Windows11 开发技术…...

go语言基础——函数、结构体、接口
由于go不是一门面向对象的语言,因此在有一些特性上和java是有一些区别的,比如go中就没有类这样的概念。下面来介绍一下go的一些特性。 结构体 结构体类似与java中的类,但又不完全一样。在类中,可以定义字段和方法,但…...
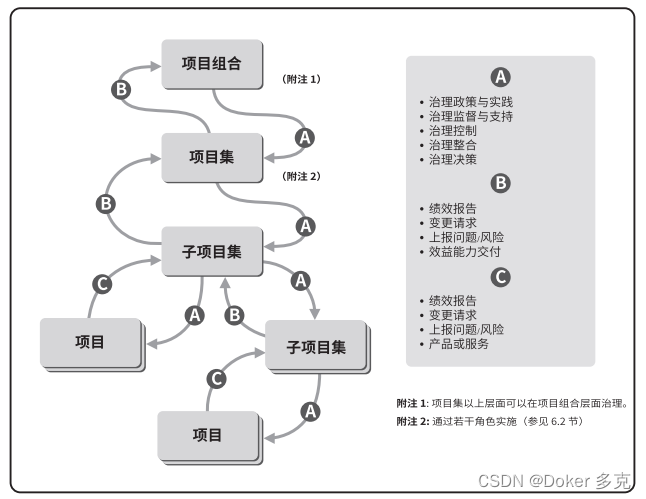
项目集管理—项目集治理
一、概述 项目集治理是实现和执行项目集决策,为支持项目集而制定实践,并维持项目集监督的绩效领域。 本章包括: 项目集治理实践项目集治理角色项目集治理设计与实施 项目集治理包括为了满足组织战略和运营目标的要求,对项目集实…...

MySQL了解之复制(一)
1.1、复制解决的问题 数据复制技术有以下一些特点: (1) 数据分布 (2) 负载平衡(load balancing) (3) 备份 (4) 高可用性(high availability)和容错 1.2、复制如何工作 从高层来看,复制分成三步: (1) master将改变记录到二进制…...

Halcon得出三角形内切圆
Halcon得出三角形内切圆 news2023/5/27 7:14: 目录 一、得出三角形的三个角点二、用类似尺规作图法得出三角形圆心 1、以三角形三角点画出圆形轮廓2、求出三角形轮廓与圆形轮廓之间的交点3、获得角平分线,三边角平分线交点为圆心三、求出圆心到边最短距离即半径 …...

2023年6月北京/广州/深圳CDGA/CDGP数据治理认证招生
DAMA认证为数据管理专业人士提供职业目标晋升规划,彰显了职业发展里程碑及发展阶梯定义,帮助数据管理从业人士获得企业数字化转型战略下的必备职业能力,促进开展工作实践应用及实际问题解决,形成企业所需的新数字经济下的核心职业…...
)
KMP 算法(Knuth-Morris-Pratt)
tip:作为程序员一定学习编程之道,一定要对代码的编写有追求,不能实现就完事了。我们应该让自己写的代码更加优雅,即使这会费时费力。 推荐:体系化学习Java(Java面试专题) 文章目录 一、什么是 …...

Java泛型详解
泛型的理解 泛型的概念 所谓泛型,就是允许在定义类、接口时通过一个标识表示类中某个属性的类型 或者是 某个方法的返回值类型及参数类型。这个类型参数将在使用时(例如,继承或实现这个接口,用这个类型声明变量、创建对象时&#…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
