搜索与图论(acwing算法基础)
文章目录
- DFS
- 排列数字
- n皇后
- BFS
- 走迷宫
- 拓扑序列
- 单链表
- 树与图的深度优先搜索
- 模拟队列
- 有向图的拓扑序列
- bellman-ford
- 有边数限制的最短路
- spfa
- spfa求最短路
- spfa判断负环
- Floyd
- Floyd求最短路
- Prim
- Prim算法求最小生成树
- Kruskal
- Kruskal算法求最小生成树
- 染色法判定二分图
- 染色法判定二分图
DFS
排列数字
#include<iostream>
using namespace std;
int n ;
int a[10];
bool s[10];
void dfs(int u)
{if(u == n){for(int i = 0 ; i <n ; i++) cout << a[i] << " " ;cout << endl ;return;}for(int i = 1; i <= n ; i++){if(!s[i]){a[u] = i;s[i] = true ;dfs(u+1);a[u] = 0 ;s[i] = false;}}}
int main()
{cin >> n ;dfs(0);return 0;
}
n皇后
#include<iostream>
using namespace std;
const int N = 20 ;
char g[N][N] ;
bool c[N], x[N] , y[N];
int n , m ;
void dfs(int u)
{if(u == n){for(int i = 0 ; i < n; i++) cout << g[i] << endl;cout << endl;return ;}for(int i = 0 ; i < n ; i++){if(!c[i] && !x[u+i] && !y[u-i+n]){c[i] = x[u+i] = y[u-i+n] = true ;g[u][i] = 'Q';dfs(u+1);g[u][i] = '.';c[i] = x[u+i] = y[u-i+n] = false ;}}
}
int main()
{cin >> n;for(int i = 0 ; i < n ; i++)for(int j = 0 ; j < n ; j++)g[i][j] = '.' ;dfs(0); return 0 ;
}
BFS
走迷宫
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int,int> PII ;
const int N = 110 ;
PII q[N * N];
int f[N][N] , d[N][N];
int n , m ;
int dx[] = {0,1,0,-1} , dy[] = {1,0,-1,0} ;
int bfs()
{memset(d , -1 , sizeof d);d[1][1] = 0 ;q[0] = {1,1};int hh = 0 , tt = 0 ;while(hh <= tt){auto t = q[hh++] ;for(int i = 0 ; i < 4 ; i++){int x = t.first + dx[i] , y = t.second + dy[i] ;if(x<=n &&x>0 && y<=m && y>0 && d[x][y] == -1 && f[x][y] == 0){q[++tt] = {x,y};d[x][y] = d[t.first][t.second] + 1 ;}}}return d[n][m];
}
int main()
{cin >> n >> m ;for(int i = 1 ; i <= n ; i++)for(int j = 1 ; j <= m ; j++)cin >> f[i][j];cout << bfs();return 0;
}
拓扑序列
单链表
点击跳转至例题

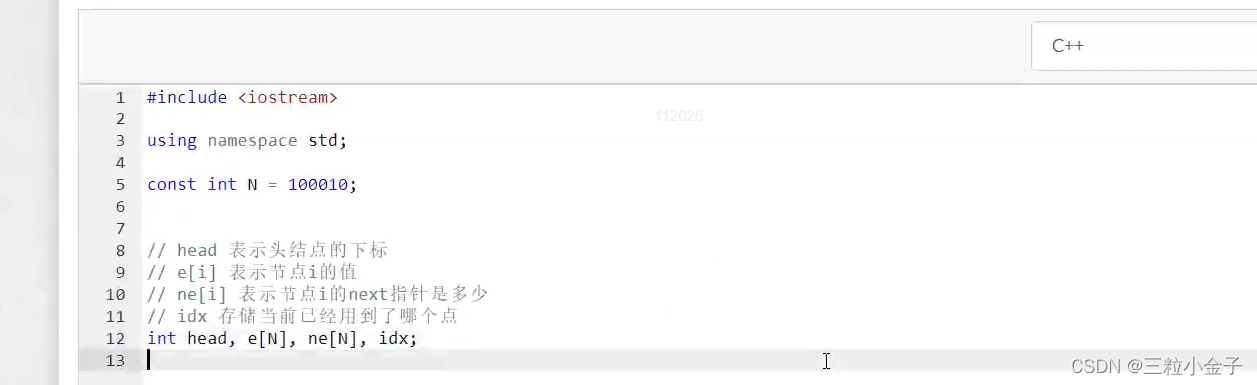
idx存的是指针
树与图的深度优先搜索
树的重心
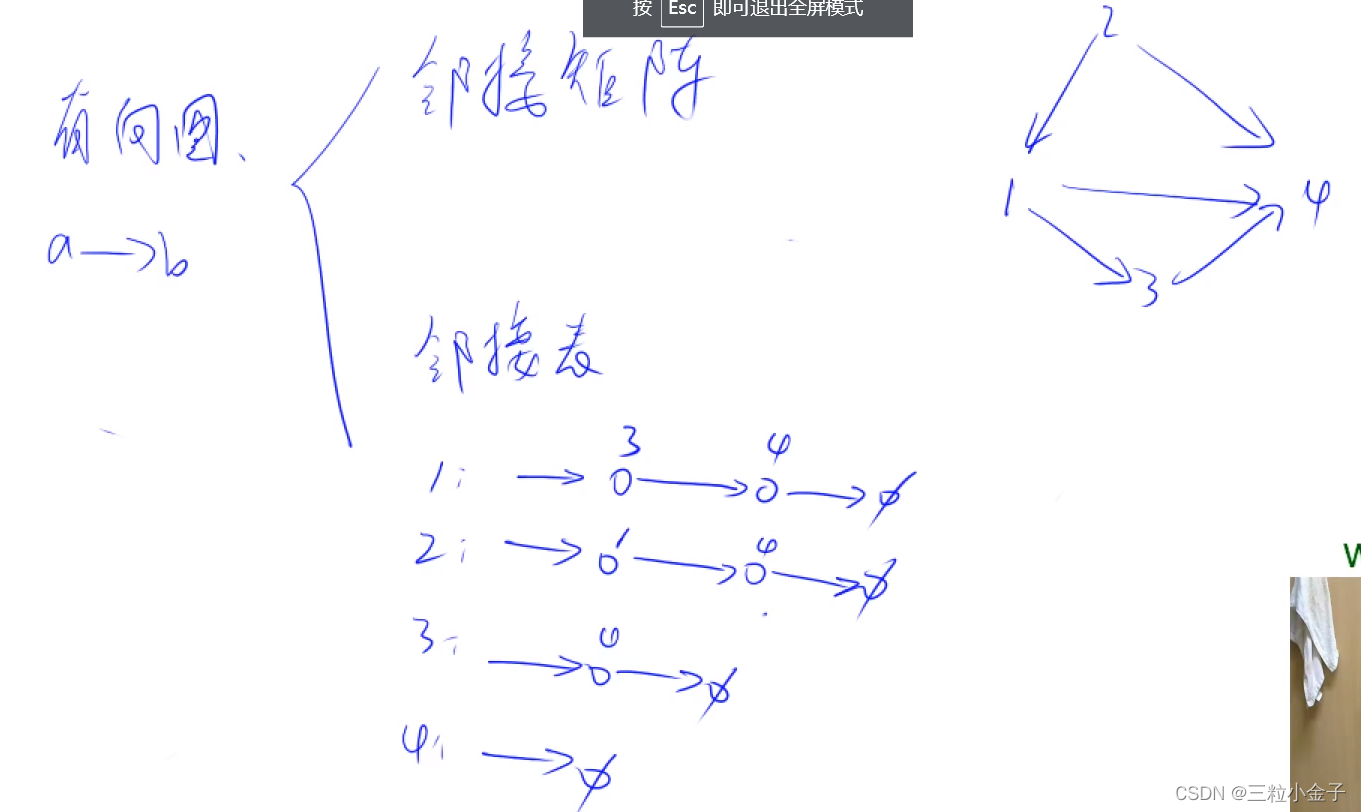
每个节点都是一个单链表
模拟队列
hh = 0 , tt = -1
有向图的拓扑序列
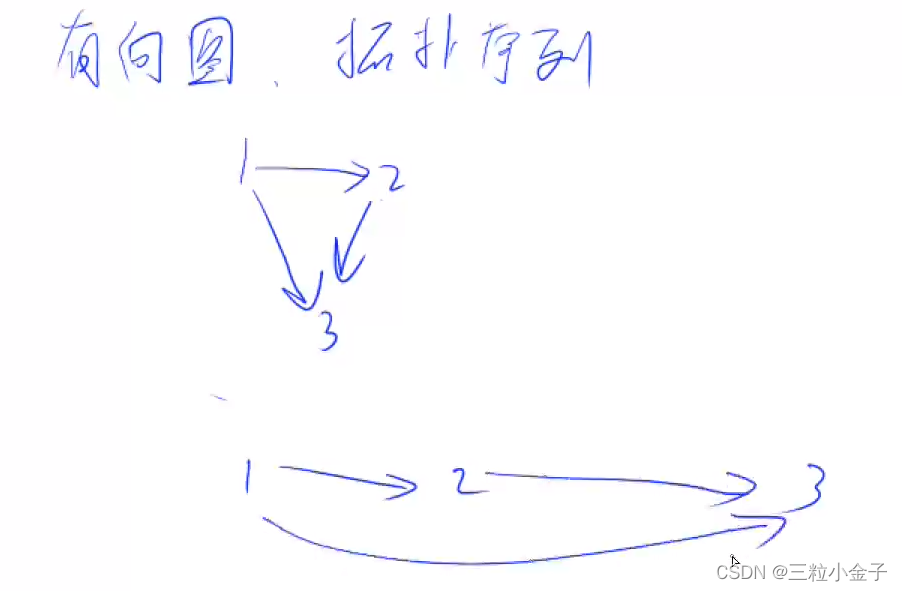
都是从前指向后,即有向无环图(不能有环)
所有入度为0的点,都能排在前面的位置

删掉t->j的边,仅仅是j的入度减一,当j的入度为0的时候,放入队列
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;
int n , m ;
int e[N] , h[N] , ne[N] , idx;
int d[N] , q[N];
void add(int a , int b)
{e[idx] = b , ne[idx] = h[a] , h[a] = idx++;
}
bool topool()
{int hh = 0 , tt = -1 ;for(int i = 1; i <= n ; i++)if(!d[i]) q[++tt] = i ;while(hh <= tt){int t = q[hh++];for(int i = h[t] ; i != -1 ; i = ne[i]){int j = e[i]; d[j] -- ;if(d[j] == 0) q[++tt] = j ;}}return tt == n - 1;
}
int main()
{cin >> n >> m ;memset(h , -1 , sizeof h) ;for(int i = 0 ; i < m ; i++){int x,y;cin >> x >> y;add(x,y);d[y]++;}if(topool()){for(int i = 0 ; i < n ; i++) cout << q[i] << " " ;}else cout << -1 ;return 0;
}
bellman-ford
有边数限制的最短路
spfa
spfa求最短路
spfa判断负环
Floyd
Floyd求最短路
Prim
Prim算法求最小生成树
Kruskal
Kruskal算法求最小生成树
染色法判定二分图
染色法判定二分图
相关文章:

搜索与图论(acwing算法基础)
文章目录 DFS排列数字n皇后 BFS走迷宫 拓扑序列单链表树与图的深度优先搜索模拟队列有向图的拓扑序列 bellman-ford有边数限制的最短路 spfaspfa求最短路spfa判断负环 FloydFloyd求最短路 PrimPrim算法求最小生成树 KruskalKruskal算法求最小生成树 染色法判定二分图染色法判定…...

【数据结构】何为数据结构。
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2022博客之星T…...

【P57】JMeter 保存响应到文件(Save Responses to a file)
文章目录 一、保存响应到文件(Save Responses to a file)参数说明二、准备工作三、测试计划设计 一、保存响应到文件(Save Responses to a file)参数说明 可以将结果树保存到文件 使用场景:当结果太大,使…...
Visual Studio 2022 v17.6 正式发布
Visual Studio 17.6 正式发布,这个最新版本提供了一系列强大的工具和功能,旨在使你能够制作出最先进的应用程序。 提高生产力 通过 Visual Studio 2022,目标是帮助你在更短的时间内完成 IDE 内的所有开发任务,在这个版本中&…...

std::chrono时间处理
std::chrono是C11引入的标准库,用于时间的计算和处理。它按照ISO8601标准定义了多个时间类,例如:duration(持续时间)、time_point(时间点)和clock(时钟)。以下是一些常见…...

ieda codeformatV2.xml
ieda codeformatV2.xml 目录概述需求: 设计思路实现思路分析1.codeformatV22.codeformatV23.codeformatV24.codeformatV25.数据处理器 拓展实现 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&…...

Hbase
java客户端 导入maven依赖 XML<dependencies> <dependency> <groupId>org.apache.zookeeper</groupId> <artifactId>zookeeper</artifactId> <version>3.4.6</version> </dependency>…...
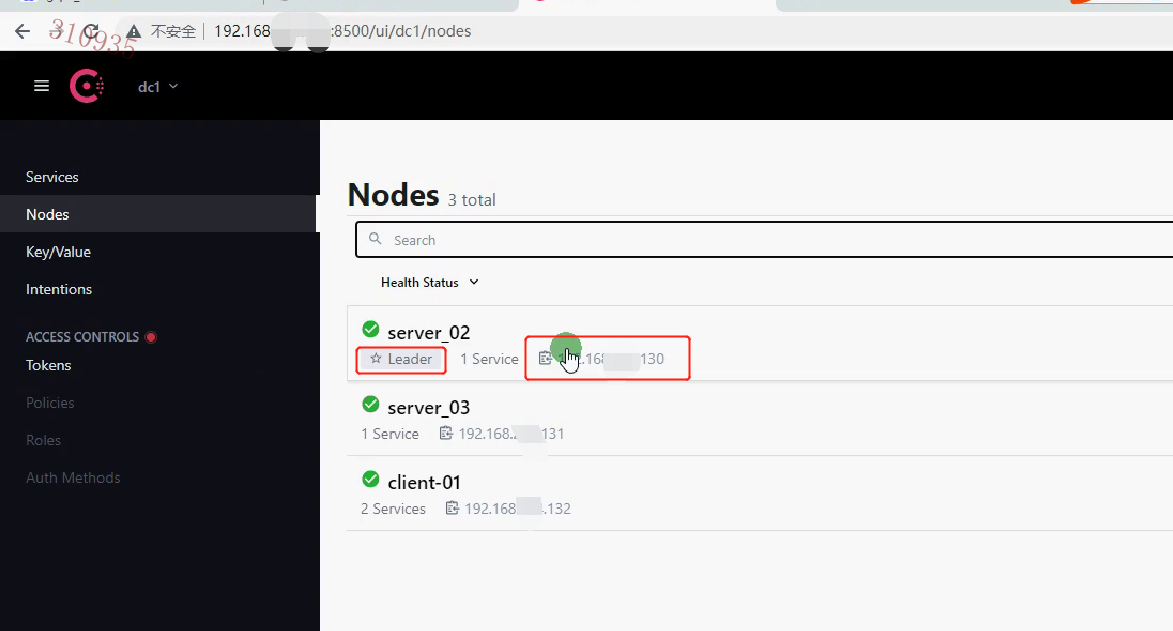
[golang 微服务] 5. 微服务服务发现介绍,安装以及consul的使用,Consul集群
一.服务发现介绍 引入 上一节讲解了使用 gRPC创建微服务,客户端的一个接口可能需要调用 N个服务,而不同服务可能存在 不同的服务器,这时,客户端就必须知道所有服务的 网络位置(ipport),来进行连接服务器操作,如下图所示: 以往的做…...

【数据结构】哈希应用
目录 一、位图 1、位图概念 2、位图实现 2.1、位图结构 2.2、比特位置1 2.3、比特位置0 2.4、检测位图中比特位 3、位图例题 3.1、找到只出现一次的整数 3.2、找到两个文件交集 3.3、找到出现次数不超过2次的所有整数 二、布隆过滤器 1、布隆过滤器提出 2、布隆过…...
【 Python 全栈开发 - WEB开发篇 - 31 】where条件查询
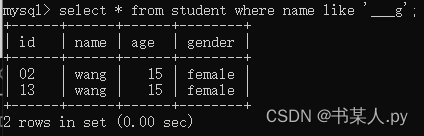
文章目录 一、where条件查询1.关系运算符查询2.IN关键字查询3.BETWEEN AND关键字查询4.空值查询5.AND关键字查询6.OR关键字查询7.LIKE关键字查询普通字符串含有%通配的字符串含有_通配的字符串 一、where条件查询 MySQL 的 where 条件查询是指在查询数据时,通过 wh…...

Android系统的Ashmem匿名共享内存子系统分析(5)- 实现共享的原理
声明 其实对于Android系统的Ashmem匿名共享内存系统早就有分析的想法,记得2019年6、7月份Mr.Deng离职期间约定一起对其进行研究的,但因为我个人问题没能实施这个计划,留下些许遗憾…文中参考了很多书籍及博客内容,可能涉及的比较…...

谈一谈冷门的C语言爬虫
C语言可以用来编写爬虫程序,但是相对于其他编程语言,C语言的爬虫开发可能会更加复杂和繁琐。因为C语言本身并没有提供现成的爬虫框架和库,需要自己编写网络请求、HTML解析等功能。 不过,如果你对C语言比较熟悉,也可以…...

基于状态的维护(CBM)如何推动设备效率提高?
基于状态的维护(Condition-Based Maintenance,CBM)是一种先进的维护策略,通过实时监测和分析设备的状态数据,预测设备故障并采取相应的维护措施。CBM基于数据驱动的方法,能够提高设备的可用性、降低维修成本…...
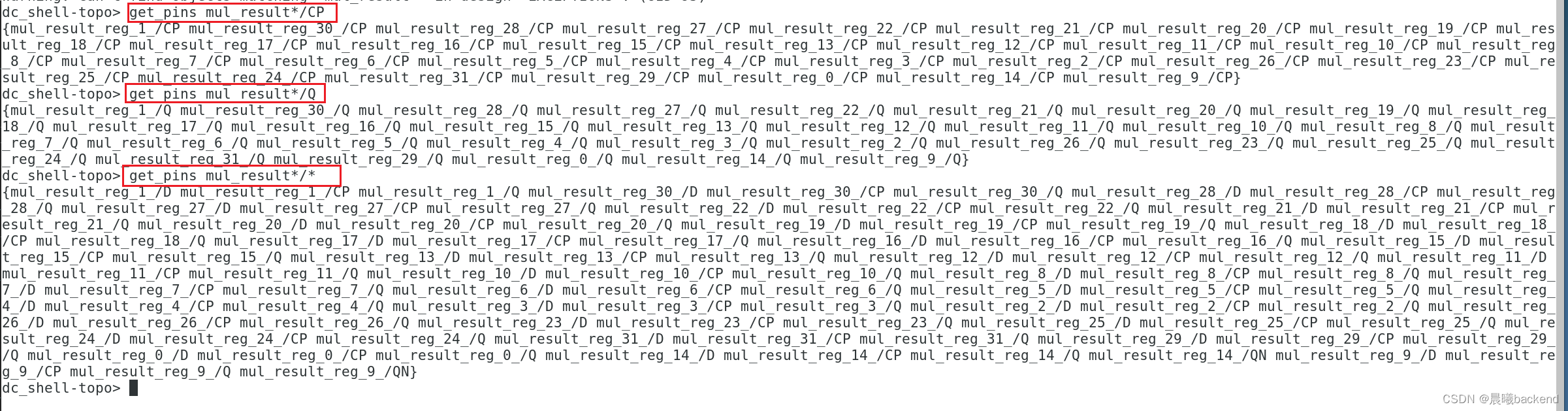
DC LAB8SDC约束四种时序路径分析
DC LAB 1.启动DC2.读入设计3. 查看所有违例的约束报告3.1 report_constraint -all_violators (alias rc)3.2 view report_constraint -all_violators -verbose -significant_digits 4 (打印详细报告) 4.查看时序报告 report_timing -significant_digits 45. 约束组合逻辑(adr_i…...

学生考试作弊检测系统 yolov8
学生考试作弊检测系统采用yolov8网络模型人工智能技术,学生考试作弊检测系统过在考场中安装监控设备,对学生的作弊行为进行实时监测。当学生出现作弊行为时,学生考试作弊检测系统将自动识别并记录信息。YOLOv8 算法的核心特性和改动可以归结为…...

【基于容器的部署、扩展和管理】 3.2 基于容器的应用程序部署和升级
往期回顾: 第一章:【云原生概念和技术】 第二章:【容器化应用程序设计和开发】 第三章:【3.1 容器编排系统和Kubernetes集群的构建】 3.2 基于容器的应用程序部署和升级 3.2 基于容器的应用程序部署和升级 3.2 基于容器的应用程…...

Jmeter 实现 grpc服务 压测
一、Jmeter安装与配置 网上有很多安装与配置文章,在此不做赘述 二、Jmeter gRPC Request 插件安装 插件下载地址:JMeter Plugins :: JMeter-Plugins.org 将下载文件解压后放到Jmeter安装目录下 /lib/ext 然后在终端输入Jmeter即可打开 Jmeter GUI界面…...
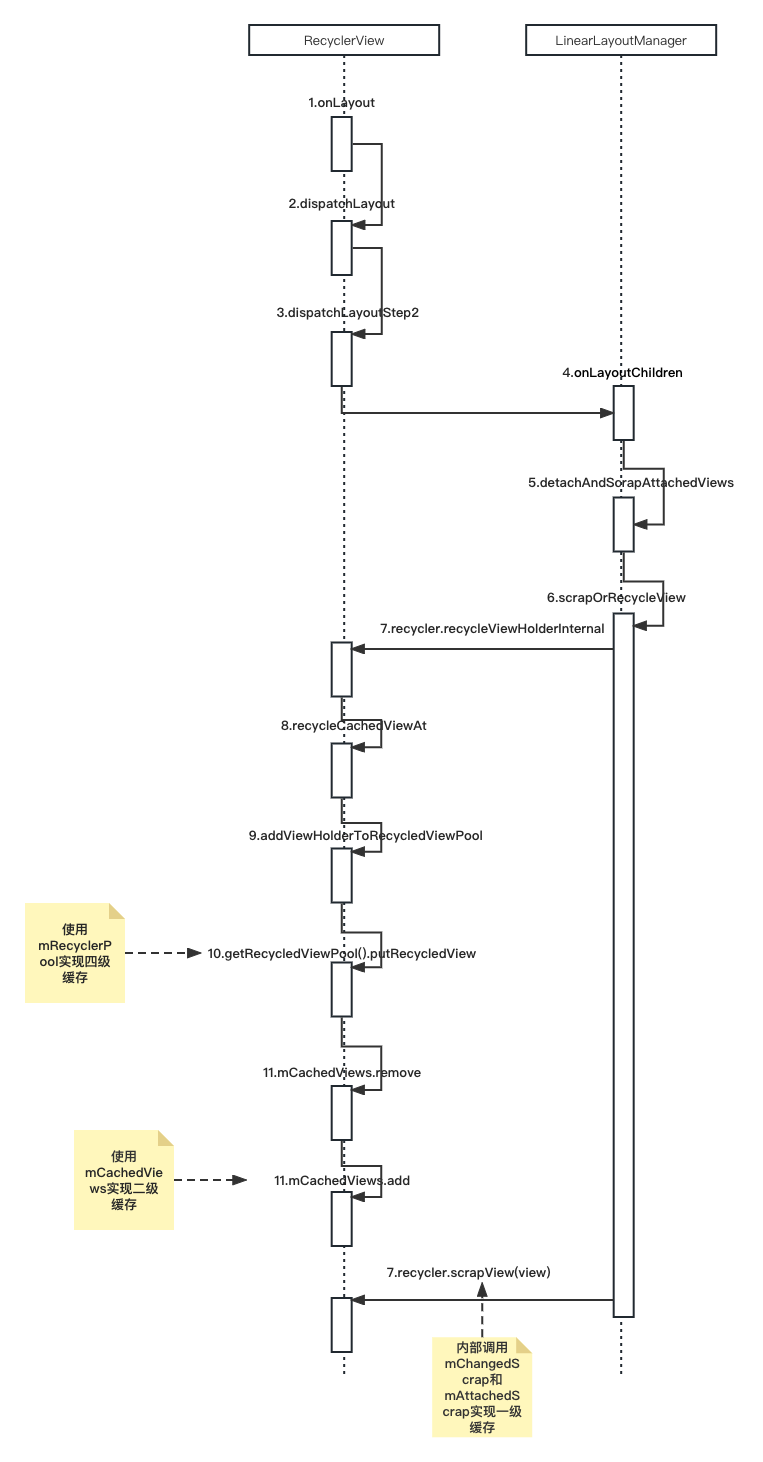
深入源码分析RecyclerView缓存复用原理
文章目录 前言四级缓存 源码分析缓存一级缓存(mChangedScrap和mChangedScrap)二级缓存(mCachedViews)三级缓存(ViewCacheExtension)四级缓存(mRecyclerPool)缓存池mRecyclerPool结构…...

内网隧道代理技术(一)之内网隧道代理概述
内网隧道代理技术 内网转发 在渗透测试中,当我们获得了外网服务器(如web服务器,ftp服务器,mali服务器等等)的一定权限后发现这台服务器可以直接或者间接的访问内网。此时渗透测试进入后渗透阶段,一般情况…...

设计图形用户界面的原则
1) 一般性原则:界面要具有一致性、常用操作要有快捷方式、 提供简单的错误处理、对操作人员的重要操作要有信息反馈、操作可 逆、设计良好的联机帮助、合理划分并高效地使用显示屏、保证信息 显示方式与数据输入方式的协调一致 2) 颜色的使用:颜色…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
