当前位置： 首页 > news >正文

单容水箱建模(自衡单容水箱+无自衡单容水箱)

news 2025/12/9 2:16:42

自衡单容水箱Simulink建模和PLC源代码请参看下面文章链接：

单容双容水箱建模(simulink仿真+PLC代码)_RXXW_Dor的博客-CSDN博客PLC通过伯努利方程近似计算水箱流量详细内容请参看下面的文章博客PLC通过伯努利方程近似计算水箱流量(FC)_怎么用伯努利方程求某水位流量_RXXW_Dor的博客-CSDN博客伯努利方程属于流体力学范畴，感兴趣的可以自行搜索，这篇博文我们直接给出PLC通过伯努利方程近似计算水箱流量的FC,FC输出体积流量m^3/s和质量流量kg/s,（通过液体的密度和体积关系完成计算）。2、模型计算............下面我们简单的看下简单2水箱模型，https://blog.csdn.net/m0_46143730/article/details/130795660

1、模型介绍

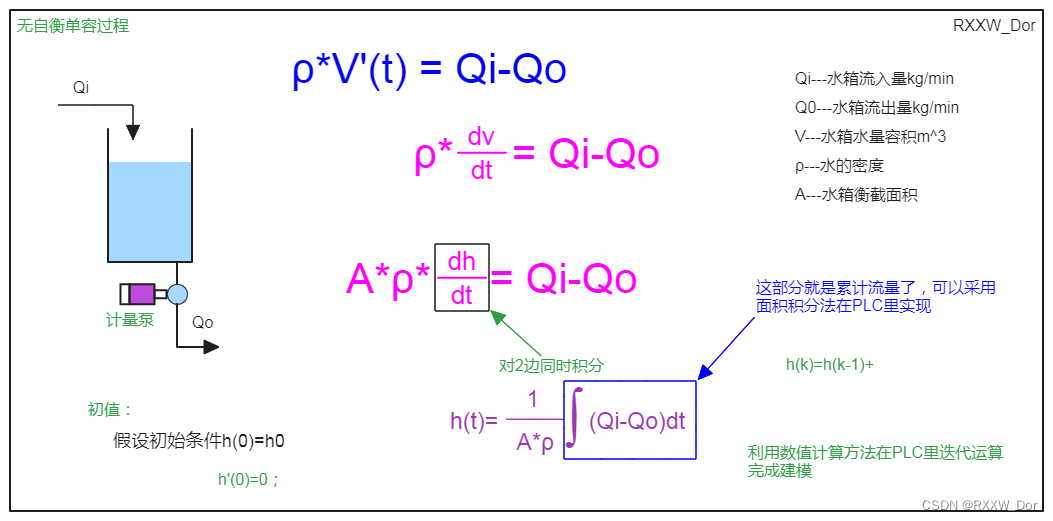无自衡单容过程的传递函数为一阶积分环节，积分作用的大小与积分时间成反比，水箱截面积越大，积分时间越长，

相关文章：

单容水箱建模(自衡单容水箱+无自衡单容水箱)

自衡单容水箱Simulink建模和PLC源代码请参看下面文章链接： 单容双容水箱建模(simulink仿真+PLC代码)_RXXW_Dor的博客-CSDN博客PLC通过伯努利方程近似计算水箱流量详细内容请参看下面的文章博客PLC通过伯努利方程近似计算水箱流量(FC)_怎么用伯努利方程求某水位流量_RXXW_Dor的…...

编程日记 2023/6/10 18:45:46

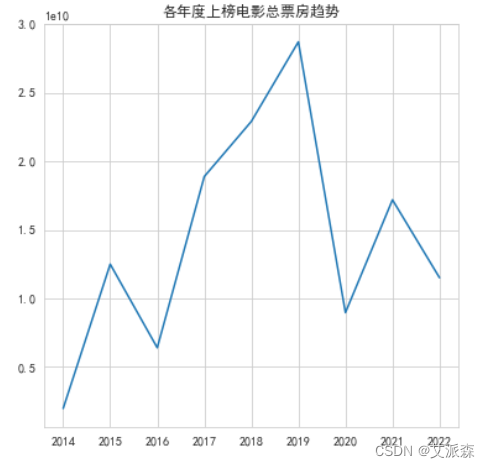
分享Python7个爬虫小案例（附源码）

本次的7个python爬虫小案例涉及到了re正则、xpath、beautiful soup、selenium等知识点，非常适合刚入门python爬虫的小伙伴参考学习。注：若涉及到版权或隐私问题，请及时联系我删除即可。 1.使用正则表达式和文件操作爬取并保存“某吧”某帖子…...

编程日记 2023/6/10 18:40:45

我用ChatGPT写2023高考语文作文（一）：全国甲卷

2023年 全国甲卷 适用地区：广西、贵州、四川、西藏 人们因技术发展得以更好地掌控时间，但也有人因此成了时间的仆人。 这句话引发了你怎样的联想与思考？请写一篇文章。 要求：选准角度，确定立意，明确文体&am…...

编程日记 2023/6/10 18:35:43

c++ modbusTCP

//Modbus TCP是一种基于TCP/IP协议的Modbus协议，它允许Modbus协议通过以太网进行通信。 //在C中，可以使用第三方库来实现Modbus TCP通信，例如libmodbus和QModbus。 //使用libmodbus库实现Modbus TCP通信的示例代码如下： //c #incl…...

编程日记 2023/6/10 18:30:42

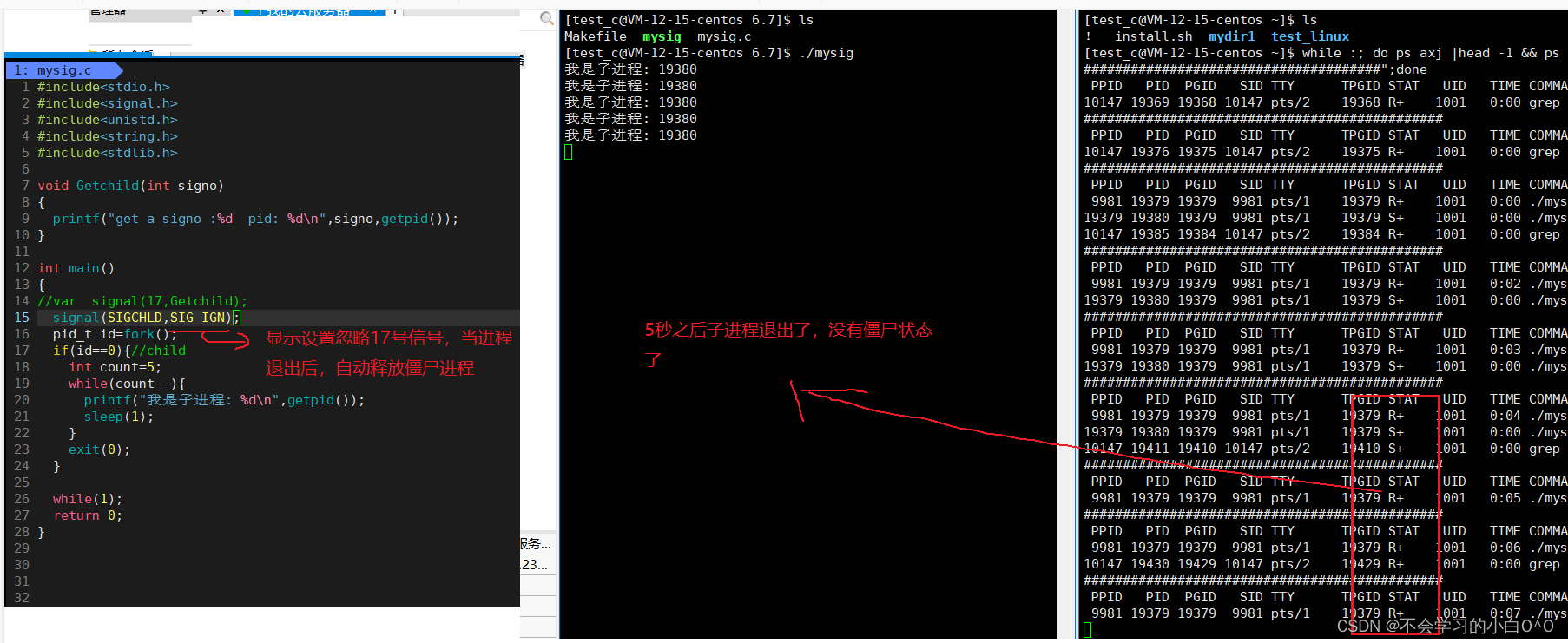
linux(信号结尾)

目录： 1.可重入函数 2.volatile关键字 3.SIGCHLD信号 -------------------------------------------------------------------------------------------------------------------------------- 1.可重入函数----------用来描述一个函数的特点的 1.在单进程当中也存…...

编程日记 2023/6/10 18:25:41

【漏洞修复】node-exporter被检测出来pprof调试信息泄露漏洞

node-exporter被检测出来pprof调试信息泄露漏洞 说在前面解决方法结语 说在前面 惯例开篇吐槽，有些二五仔习惯搞点自研的安全扫描工具，然后加点DIY元素，他也不管扫的准不准，就要给你报个高中危的漏洞，然后就要去修复&…...

编程日记 2023/6/10 18:20:40

在linux 上安装 NFS服务器软件

在 Ubuntu Linux 中创建 NFS 文件系统通常需要完成以下步骤： 安装 NFS 服务器软件。您可以在终端上使用以下命令来安装所需的软件包。sudo apt-get update sudo apt-get install nfs-kernel-server创建要共享的目录。例如，您可以创建一个名为 /var/nfs/shared 的目录。sudo m…...

编程日记 2023/6/10 18:15:38

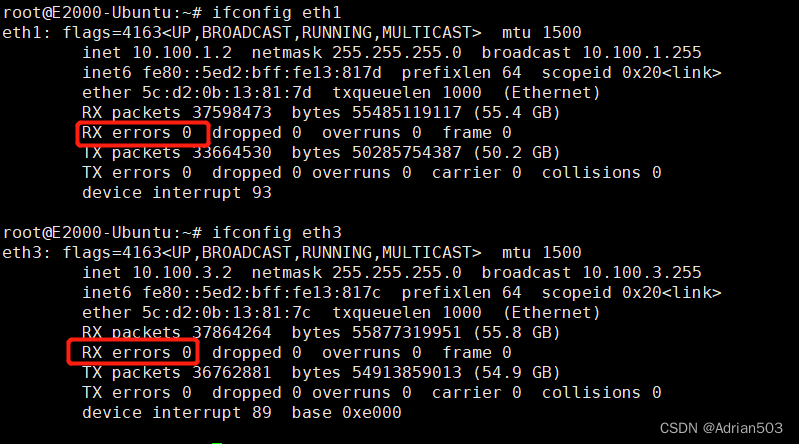
网卡中的Ring buffer -- 解决 rx_resource_errors 丢包

1、软硬件环境 硬件&#xff1a; 飞腾E2000Q 平台 软件&#xff1a; linux 4.19.246 2、问题现象 网卡在高速收包的过程中&#xff0c;出现 rx error , 细查是 rx_resource_errors 如下&#xff1a; rootE2000-Ubuntu:~# ifconfig eth1 eth1: flags4163<UP,BROADCAST,RU…...

编程日记 2023/6/10 18:10:37

六月九号补题日记：Codeforces Round 877 (Div. 2)

专注是不够的&#xff0c;很重要的一方面在于细节&#xff0c;关注细节&#xff1a;精细和专注才是成功的重点&#xff01;&#xff01;&#xff01; A 题意&#xff1a;给你一堆数字&#xff0c;说这一堆数字是由最初的两个数字相减得到的&#xff0c;让你求出两个数字其中一…...

编程日记 2023/6/10 18:05:36

python基础选择题，高中适用

1. 下面哪个是 Python 的注释符号&#xff1f; A. // B. # C. /* D. ; 答案&#xff1a;B 2. 下面哪个是 Python 的赋值运算符&#xff1f; A. B. C. ! D. > 答案&#xff1a;A 3. 下面哪个是 Python 的逻辑运算符&#xff1f; A. && B. || C. ! D. & 答…...

编程日记 2023/6/10 18:00:35

Linux 面试题-(腾讯,百度,美团,滴滴)

Linux 面试题-(腾讯,百度,美团,滴滴) 分析日志t.log(访问量)&#xff0c;将各个ip 地址截取&#xff0c;并统计出现次数,并按从大到小排序(腾讯) http://192.168.200.10/index1.html http://192.168.200.10/index2.html http://192.168.200.20/index1.html http://192.168.20…...

编程日记 2023/6/10 17:55:34

DDD--战略设计步骤

在领域驱动设计&#xff08;Domain-Driven Design&#xff0c;DDD&#xff09;中&#xff0c;战略设计是指在系统的整体层面上考虑领域模型的组织和架构。下面是一些战略设计的详细步骤&#xff1a; 确定限界上下文&#xff08;Bounded Context&#xff09;&#xff1a;首先&a…...

编程日记 2023/6/10 17:50:33

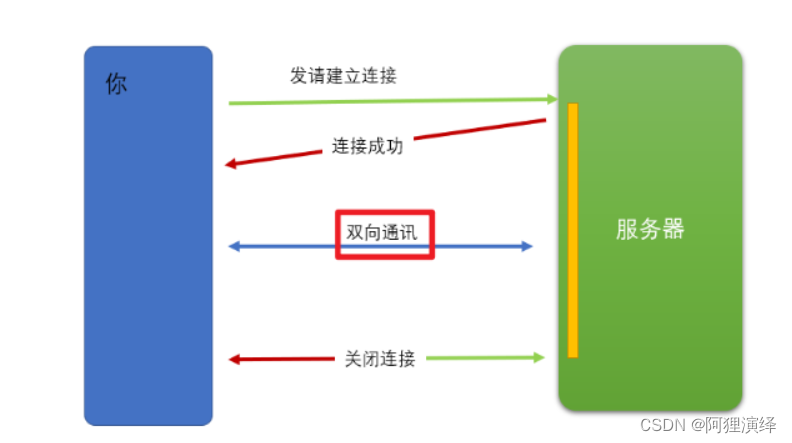
Web Scoket简述

Web Socket 简介 初次接触 Web Socket 的人&#xff0c;我们已经有了 HTTP 协议&#xff0c;为什么还需要另一个协议&#xff1f;它能带来什么好处&#xff1f; 因为 HTTP 协议有一个缺陷&#xff1a;通信只能由客户端发起。http基于请求响应实现。 &#xff08;准确来说HTTP…...

编程日记 2023/6/10 17:45:32

“Docker 技术在企业中的应用及挑战解决方案“

Docker 技术是一种基于容器化的应用部署和管理技术。随着云计算的普及和应用的不断增多&#xff0c;Docker 技术在企业中的应用越来越广泛。本文将介绍 Docker 技术的基本概念、优势和应用场景&#xff0c;并讨论如何在企业中应用 Docker 技术。 一、Docker 技术概述 Docker …...

编程日记 2023/6/10 17:40:31

vue中开发包、生产包、全局包的区别以及安装语法

目录 开发包 (devDependencies) 安装方法 生产包 (dependencies) 安装方法 全局包 (Global build) 安装方法 vue中有三种不同类型的包&#xff1a;开发包 (Development build)&#xff0c;生产包 (Production build) 和全局包 (Global build)。下面我们分别解释它们的区别…...

编程日记 2023/6/10 17:35:30

list的模拟实现

前言 list是STL中重要的容器&#xff0c;了解它的原理对于我们掌握它是有很多的帮助的&#xff0c;一般list和vector都是一起来使用的&#xff0c;因为它们的优缺点不同&#xff0c;刚好可以互补。list的优点是任意位置的插入和删除都很快&#xff0c;它的缺点是不支持随机访问…...

编程日记 2023/6/10 17:30:29

ChatGLM简介和SSE聊天接口测试效果

开发公司 智谱AI是由清华大学计算机系技术成果转化而来的公司&#xff0c;致力于打造新一代认知智能通用模型。公司合作研发了双语千亿级超大规模预训练模型GLM-130B&#xff0c;并构建了高精度通用知识图谱&#xff0c;形成数据与知识双轮驱动的认知引擎&#xff0c;基于此模型…...

编程日记 2023/6/10 17:25:27

darknet yolo标注、训练详细说明

文章目录 1、标注数据1.1、标注1.2、生成训练列表文件train.txt1.3、转换数据标注格式 2、训练数据整理2.1、修改train.txt路径2.2、修改yolov3.cfg2.3、obj.name和obj.data2.4、训练脚本文件trian.sh2.5、测试脚本文件test.sh 3、训练 本文对应的脚本文件和程序下载链接 darke…...

编程日记 2023/6/10 17:20:26

chatgpt赋能python：Python如何产生随机整数？

Python如何产生随机整数&#xff1f; Python是一种高级编程语言。它允许程序员轻松地创建各种类型的应用程序&#xff0c;包括生成随机整数。本文将介绍如何在Python中使用内置的随机数函数来生成随机整数。 random模块 Python中的random模块提供了生成随机数的函数。这些函…...

编程日记 2023/6/10 17:15:26

大话Stable-Diffusion-Webui-客制化主题（四）

文章目录 目标效果开始重要说明单选框以及复选框图标样式更改gradio主题构建器上传主题方式代码上传主题方式目标 在DIY的主题中更改gradio单选框组件以及复选框组件的勾选后图标样式 效果 开始 笔者在使用gradio的主题构建器的过程中发现，gradio的复选框以及单选框组件勾选…...

编程日记 2023/6/10 17:10:24

React Native在HarmonyOS 5.0阅读类应用开发中的实践

一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强&#xff0c;React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 &#xff08;1&#xff09;使用React Native…...

编程新知 2025/8/19 2:57:37

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2025/11/27 12:34:52

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具

第2章 虚拟机性能监控&#xff0c;故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令&#xff1a;jps [options] [hostid] 功能&#xff1a;本地虚拟机进程显示进程ID&#xff08;与ps相同&#xff09;&#xff0c;可同时显示主类&#x…...

编程新知 2025/12/5 18:12:58

学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”

2025年#高考 将在近日拉开帷幕&#xff0c;#AI 监考一度冲上热搜。当AI深度融入高考&#xff0c;#时间同步 不再是辅助功能&#xff0c;而是决定AI监考系统成败的“生命线”。 AI亮相2025高考&#xff0c;40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕&#xff0c;江西、…...

编程新知 2025/12/7 13:19:35

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理）

上一章用到了V2 的概念&#xff0c;其实 Fiori当中还有 V4&#xff0c;咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务)&#xff0c;代理中间件&#xff08;ui5-middleware-simpleproxy&#xff09;-CSDN博客…...

编程新知 2025/12/6 5:30:57

【笔记】WSL 中 Rust 安装与测试完整记录

#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统&#xff1a;Ubuntu 24.04 LTS (WSL2)架构&#xff1a;x86_64 (GNU/Linux)Rust 版本&#xff1a;rustc 1.87.0 (2025-05-09)Cargo 版本&#xff1a;cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

编程新知 2025/11/28 6:00:25

C++课设：简易日历程序（支持传统节假日 + 二十四节气 + 个人纪念日管理）

名人说：路漫漫其修远兮，吾将上下而求索。—— 屈原《离骚》 创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊） 专栏介绍：《编程项目实战》 目录 一、为什么要开发一个日历程序？1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

编程新知 2025/7/20 6:08:51

Spring AI Chat Memory 实战指南：Local 与 JDBC 存储集成

一个面向 Java 开发者的 Sring-Ai 示例工程项目&#xff0c;该项目是一个 Spring AI 快速入门的样例工程项目&#xff0c;旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计&#xff0c;每个模块都专注于特定的功能领域&#xff0c;便于学习和…...

编程新知 2025/10/16 14:46:22

规则与人性的天平——由高考迟到事件引发的思考

当那位身着校服的考生在考场关闭1分钟后狂奔而至&#xff0c;他涨红的脸上写满绝望。铁门内秒针划过的弧度&#xff0c;成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定"&#xff0c;构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

编程新知 2025/10/6 19:47:32

向量几何的二元性：叉乘模长与内积投影的深层联系

在数学与物理的空间世界中&#xff0c;向量运算构成了理解几何结构的基石。叉乘&#xff08;外积&#xff09;与点积&#xff08;内积&#xff09;作为向量代数的两大支柱&#xff0c;表面上呈现出截然不同的几何意义与代数形式&#xff0c;却在深层次上揭示了向量间相互作用的…...

编程新知 2025/12/2 18:03:39