【代码随想录】刷题Day53
1.最长公共子序列
1143. 最长公共子序列
和之前的一道题目的区别就是这个子序列不需要每个字符相邻。那么条件就变成两种了,一种是当前的字符相同,一种是不同。相同跟之前的条件一样;不同则需要继承上次比较的较大值。if (text1[i - 1] == text2[j - 1]),则dp[i][j] = dp[i - 1][j - 1] + 1;此外就是继承的写法,就是i-1和j-1的字符不一样,那么就是 看i-2和j-1字符组成的大小 以及 i-1和j-2字符组成的大小之间比较的大小取舍,即dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i < text1.size() + 1; i++){for (int j = 1; j < text2.size() + 1; j++){if (text1[i - 1] == text2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}}return dp[text1.size()][text2.size()];}
};2.不相交的线
1035. 不相交的线
跟上一题其实是一样的,因为本质都是往后找子列
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));for (int i = 1; i < nums1.size() + 1; i++){for (int j = 1; j < nums2.size() + 1; j++){if (nums1[i - 1] == nums2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}}return dp[nums1.size()][nums2.size()];}
};3.最大子数组和
53. 最大子数组和
1.会超出存储范围的dp,其实思路就是暴力解,只是表达式简单易懂。
2.dp[i][j]:从i到j位置的最大子数组和。
3.那么i<j的位置其实都是没有意义的。只考虑二维数组的另外一半。条件其实很简单,就是比较加上j这个节点的数组会不会子数组更大,所以条件为dp[i][j] = dp[i][j - 1] + nums[j];
4.初始化就是:将dp[i][i]位置的数变为nums[i];dp[0][i]为前一个数的累加dp[0][i] = dp[0][i - 1] + nums[i];
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<vector<int>>dp(nums.size(), vector<int>(nums.size(), 0));dp[0][0] = nums[0];for (int i = 1; i < nums.size(); i++){dp[0][i] = dp[0][i - 1] + nums[i];}int ret = nums[0];for (int i = 0; i < nums.size(); i++){dp[i][i] = nums[i];ret = max(ret, dp[i][i]);for (int j = i + 1; j < nums.size(); j++){dp[i][j] = dp[i][j - 1] + nums[j];ret = max(ret, dp[i][j]);}}return ret;}
};1.dp[i]:为i位置的最大子数组和
2.条件:就是看前面一个dp加上当前节点和单独是该节点的数之间的比较dp[i] = max(dp[i - 1] + nums[i], nums[i]);
3.初始化dp[0] = nums[0];
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int>dp(nums.size(), 0);dp[0] = nums[0];int ret = dp[0];for (int i = 1; i < nums.size(); i++){dp[i] = max(dp[i - 1] + nums[i], nums[i]);ret = max(ret, dp[i]);}return ret;}
};相关文章:

【代码随想录】刷题Day53
1.最长公共子序列 1143. 最长公共子序列 和之前的一道题目的区别就是这个子序列不需要每个字符相邻。那么条件就变成两种了,一种是当前的字符相同,一种是不同。相同跟之前的条件一样;不同则需要继承上次比较的较大值。if (text1[i - 1] tex…...

MySQL 索引及查询优化总结
一个简单的对比测试 前面的案例中,c2c_zwdb.t_file_count表只有一个自增id,FFileName字段未加索引的sql执行情况如下: 在上图中,typeall,keynull,rows33777。该sql未使用索引,是一个效率非常低…...
什么是AJAX?
AJAX是一种基于Web的技术,它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX,Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。 AJAX是Asynchronous JavaScript and XML的缩写。尽管…...

报表生成器FastReport .Net用户指南:显示数据列、HTML标签
FastReport .Net是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。 FastReport.NET官方版…...

bootstrap-dialog弹框,去掉遮盖层,可移动
1.去掉遮盖层的设置data-backdrop"false" <div class"modal fade" id"modal" aria-modal"true" role"dialog" data-backdrop"false" style"width:50%"><div class"modal-dialog modal-l…...

7. user-Agent破解反爬机制
文章目录 1. 为什么要设置反爬机制2. 服务器如何区分浏览器访问和爬虫访问3. 反爬虫机制4. User-Agent是什么5. 如何查询网页的User-Agent6. user-agent信息解析7. 爬虫程序user-agent和浏览器user-agent的区别8. 代码查看爬虫程序的user-agent9. 在代码中加入请求头信息 1. 为…...

3.Nginx+Tomcat负载均衡和动静分离群集
文章目录 NginxTomcat负载均衡和动静分离群集Nginx作用实验七层反向代理nginx动静分离四层反向代理负载均衡 NginxTomcat负载均衡和动静分离群集 Nginx是-款非常优秀的HTTP服务器软件 支持高达50 000个并发连接数的响应拥有强大的静态资源处理能力运行稳定内存、CPU等系统资源…...
数据结构与算法之树结构
目录 为什么要使用树结构树结构基本概念树的种类树的存储与表示常见的一些树的应用场景为什么要使用树结构 线性结构中不论是数组还是链表,他们都存在着诟病;比如查找某个数必须从头开始查,消耗较多的时间。使用树结构,在插入和查找的性能上相对都会比线性结构要好 树结构…...

【python】 用来将对象持久化的 pickle 模块
pickle 模块可以对一个 Python 对象的二进制进行序列化和反序列化。说白了,就是它能够实现任意对象与二进制直接的相互转化,也可以实现对象与文本之间的相互转化。 比如,我程序里有一个 python 对象,我想把它存到磁盘里ÿ…...

【博客654】prometheus配置抓取保护以防止压力过载
prometheus抓取保护配置以防止压力过载 场景 担心您的应用程序指标可能突然激增,以及指标突然激增导致prometheus压力过载 就像生活中的许多事情一样,标签要有节制。当带有用户 ID 或电子邮件地址的标签被添加到指标时,虽然它不太可能结束…...

Backtrader官方中文文档:第十三章Observers观察者
本文档参考backtrader官方文档,是官方文档的完整中文翻译,可作为backtrader中文教程、backtrader中文参考手册、backtrader中文开发手册、backtrader入门资料使用。 本章包含 backtrader 官方Observers章节全部内容,入口 : https://backtrader.com/docu/observers-and-sta…...

算法leetcode|54. 螺旋矩阵(rust重拳出击)
文章目录 54. 螺旋矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java:每次循环移动一步:每次循环完成一个顺时针:…...
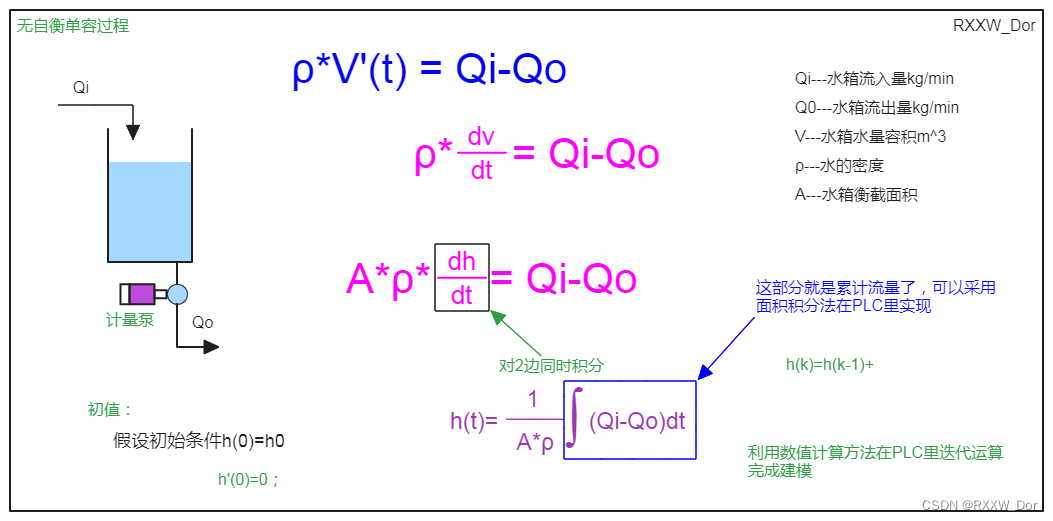
单容水箱建模(自衡单容水箱+无自衡单容水箱)
自衡单容水箱Simulink建模和PLC源代码请参看下面文章链接: 单容双容水箱建模(simulink仿真+PLC代码)_RXXW_Dor的博客-CSDN博客PLC通过伯努利方程近似计算水箱流量详细内容请参看下面的文章博客PLC通过伯努利方程近似计算水箱流量(FC)_怎么用伯努利方程求某水位流量_RXXW_Dor的…...
分享Python7个爬虫小案例(附源码)
本次的7个python爬虫小案例涉及到了re正则、xpath、beautiful soup、selenium等知识点,非常适合刚入门python爬虫的小伙伴参考学习。注:若涉及到版权或隐私问题,请及时联系我删除即可。 1.使用正则表达式和文件操作爬取并保存“某吧”某帖子…...

我用ChatGPT写2023高考语文作文(一):全国甲卷
2023年 全国甲卷 适用地区:广西、贵州、四川、西藏 人们因技术发展得以更好地掌控时间,但也有人因此成了时间的仆人。 这句话引发了你怎样的联想与思考?请写一篇文章。 要求:选准角度,确定立意,明确文体&am…...

c++ modbusTCP
//Modbus TCP是一种基于TCP/IP协议的Modbus协议,它允许Modbus协议通过以太网进行通信。 //在C中,可以使用第三方库来实现Modbus TCP通信,例如libmodbus和QModbus。 //使用libmodbus库实现Modbus TCP通信的示例代码如下: //c #incl…...
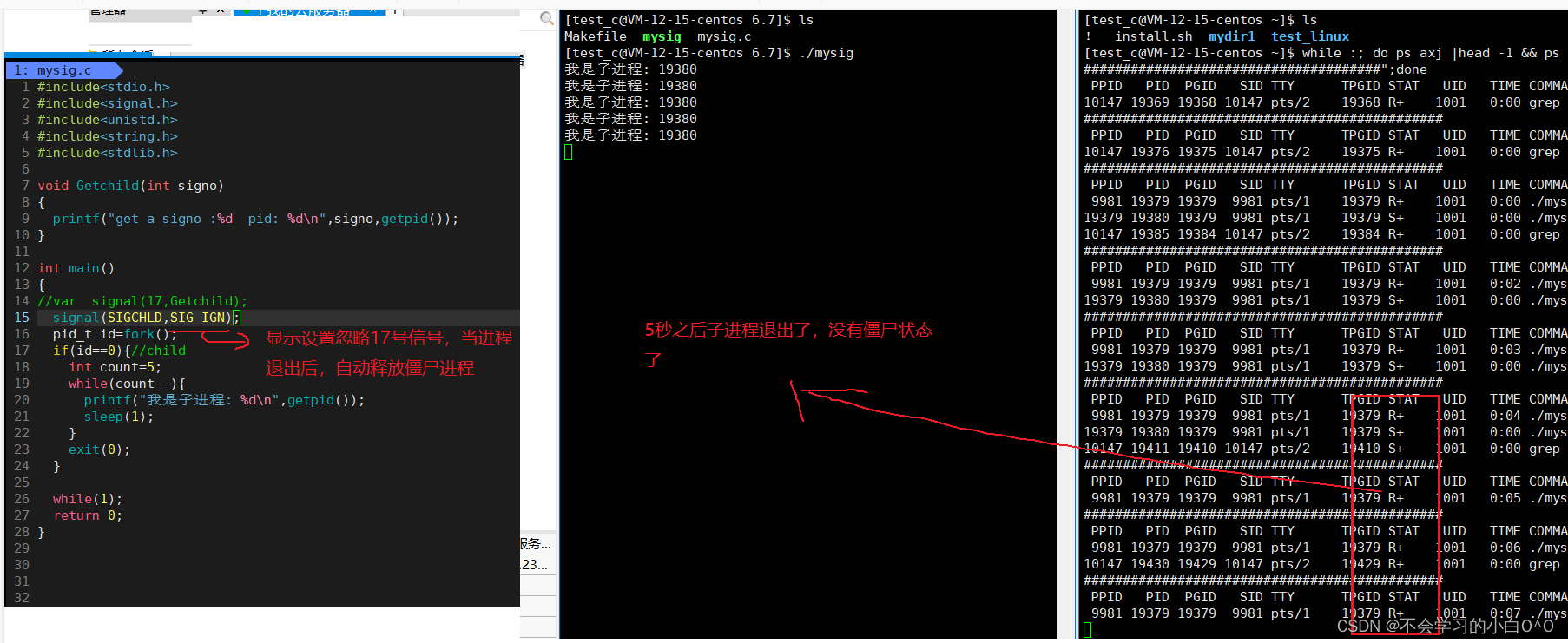
linux(信号结尾)
目录: 1.可重入函数 2.volatile关键字 3.SIGCHLD信号 -------------------------------------------------------------------------------------------------------------------------------- 1.可重入函数----------用来描述一个函数的特点的 1.在单进程当中也存…...
【漏洞修复】node-exporter被检测出来pprof调试信息泄露漏洞
node-exporter被检测出来pprof调试信息泄露漏洞 说在前面解决方法结语 说在前面 惯例开篇吐槽,有些二五仔习惯搞点自研的安全扫描工具,然后加点DIY元素,他也不管扫的准不准,就要给你报个高中危的漏洞,然后就要去修复&…...

在linux 上安装 NFS服务器软件
在 Ubuntu Linux 中创建 NFS 文件系统通常需要完成以下步骤: 安装 NFS 服务器软件。您可以在终端上使用以下命令来安装所需的软件包。sudo apt-get update sudo apt-get install nfs-kernel-server创建要共享的目录。例如,您可以创建一个名为 /var/nfs/shared 的目录。sudo m…...
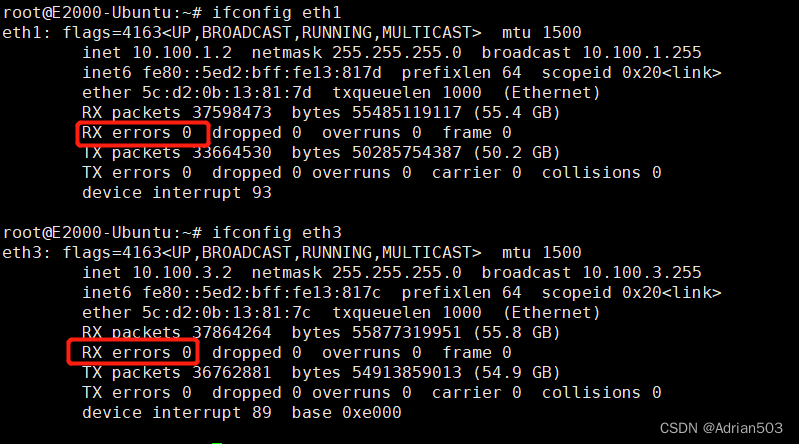
网卡中的Ring buffer -- 解决 rx_resource_errors 丢包
1、软硬件环境 硬件: 飞腾E2000Q 平台 软件: linux 4.19.246 2、问题现象 网卡在高速收包的过程中,出现 rx error , 细查是 rx_resource_errors 如下: rootE2000-Ubuntu:~# ifconfig eth1 eth1: flags4163<UP,BROADCAST,RU…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
