【运筹优化】最短路算法之A星算法 + Java代码实现
文章目录
- 一、A星算法简介
- 二、A星算法思想
- 三、A星算法 java代码
- 四、测试
一、A星算法简介
A*算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。
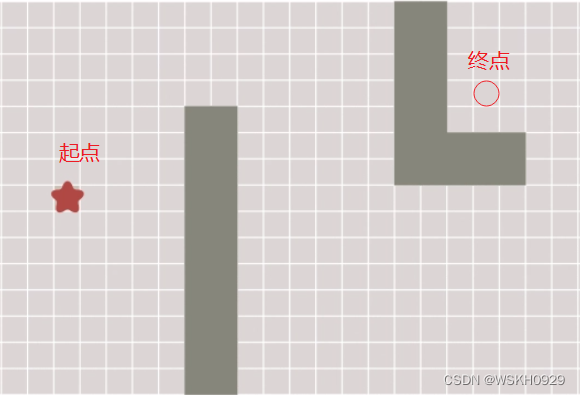
二、A星算法思想
A星(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是许多其他问题的常用启发式算法。注意——是最有效的直接搜索算法,之后涌现了很多预处理算法(如CH),在线查询效率是A*算法的数千甚至上万倍。
A*算法通过下面这个函数来计算每个节点的优先级, f ( n ) f(n) f(n) 越小,状态 n n n 被选择的优先级就越大:
公式表示为: f ( n ) = g ( n ) + h ′ ( n ) f(n)=g(n)+h'(n) f(n)=g(n)+h′(n),
- f ( n ) f(n) f(n) 是从初始状态经由状态 n n n 到目标状态的最小代价估计,
- g ( n ) g(n) g(n) 是在状态空间中从初始状态到状态 n n n 的最小代价,
- h ′ ( n ) h'(n) h′(n) 是从状态 n n n 到目标状态的路径的最小估计代价。(对于路径搜索问题,状态就是图中的节点,代价就是距离)
假设 h ( n ) h(n) h(n) 为状态 n n n 到目标状态的路径的最小真实代价。
则保证找到最短路径(最优解的)条件,关键在于估价函数 f ( n ) f(n) f(n) 的选取(或者说 h ′ ( n ) h'(n) h′(n) 的选取)。
以 h ′ ( n ) h'(n) h′(n) 表达状态 n n n 到目标状态估计的距离,那么 h ′ ( n ) h'(n) h′(n) 的选取大致有如下三种情况:
- 如果 h ′ ( n ) < h ( n ) h'(n)< h(n) h′(n)<h(n) ,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。
- 如果 h ′ ( n ) = h ( n ) h'(n)=h(n) h′(n)=h(n) ,此时的搜索效率是最高的。
- 如果 h ′ ( n ) > h ( n ) h'(n)>h(n) h′(n)>h(n) ,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
三、A星算法 java代码
@Data
public class AStar {// 0是路 1是墙 2是起点 3是终点private int[][] map;// 起点坐标int startI;int startJ;// 终点坐标int endI;int endJ;public AStar(int[][] map) {this.map = map;// 获取起点和终点坐标for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[i].length; j++) {if(map[i][j]==2){startI = i;startJ = j;}if(map[i][j]==3){endI = i;endJ = j;}}}}public void solve(){boolean[][] active = new boolean[map.length][map[0].length];PriorityBlockingQueue<Node> priorityBlockingQueue = new PriorityBlockingQueue<>();// 从起点出发ArrayList<int[]> initPath = new ArrayList<>();initPath.add(new int[]{startI,startJ});priorityBlockingQueue.add(new Node(startI,startJ,initPath,caculateDistance(startI,startJ)));active[startJ][startJ] = true;// 开始循环while (!priorityBlockingQueue.isEmpty()){Node node = priorityBlockingQueue.poll();if(node.getI()==endI && node.getJ()==endJ){for (int[] p : node.getPath()) {System.out.println(Arrays.toString(p));}System.out.println("最短路长度为:"+node.getPath().size());break;}// 向四周进行扩充// 上int i1 = node.getI()-1;int j1 = node.getJ();if(isAble(i1,j1,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i1,j1});priorityBlockingQueue.add(new Node(i1,j1,path,caculateDistance(i1,j1)));active[i1][j1] = true;}// 下int i2 = node.getI()+1;int j2 = node.getJ();if(isAble(i2,j2,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i2,j2});priorityBlockingQueue.add(new Node(i2,j2,path,caculateDistance(i2,j2)));active[i2][j2] = true;}// 左int i3 = node.getI();int j3 = node.getJ()-1;if(isAble(i3,j3,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i3,j3});priorityBlockingQueue.add(new Node(i3,j3,path,caculateDistance(i3,j3)));active[i3][j3] = true;}// 右int i4 = node.getI();int j4 = node.getJ()+1;if(isAble(i4,j4,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i4,j4});priorityBlockingQueue.add(new Node(i4,j4,path,caculateDistance(i4,j4)));active[i4][j4] = true;}}}// 判断坐标是否可行private boolean isAble(int i,int j,boolean[][] active){if(i<0 || i>=map.length){return false;}if(j<0 || j>= map[0].length){return false;}if(map[i][j]==1 || active[i][j]){return false;}return true;}// 计算距离终点的曼哈顿private int caculateDistance(int i,int j){return Math.abs(i-endI)+Math.abs(j-endJ);}@Data@NoArgsConstructor@AllArgsConstructorclass Node implements Comparable<Node>{int i;int j;List<int[]> path;// 距离终点的曼哈顿距离int lenToEnd;@Overridepublic int compareTo(Node o) {return Integer.compare(lenToEnd+path.size(),o.lenToEnd+o.path.size());}@Overridepublic String toString() {return "Node{" +"i=" + i +", j=" + j +", lenToEnd=" + lenToEnd +'}';}}
}
四、测试
public class Test {public static void main(String[] args) {long start = System.currentTimeMillis();int[][] map = new int[][]{{1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0},{0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0},{0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0},{0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0},{0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1},{0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1},{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 0, 0, 0, 0, 0},};new AStar(map).solve();System.out.println("用时:"+(System.currentTimeMillis()-start)+"ms");}
}
控制台输出:
[1, 4]
[1, 5]
[1, 6]
[1, 7]
[1, 8]
[1, 9]
[2, 9]
[2, 10]
[2, 11]
[3, 11]
[4, 11]
[5, 11]
[6, 11]
[7, 11]
[8, 11]
[9, 11]
[10, 11]
[10, 12]
[11, 12]
[12, 12]
[12, 11]
[13, 11]
[14, 11]
[15, 11]
[16, 11]
[17, 11]
[17, 12]
[17, 13]
[17, 14]
[18, 14]
[19, 14]
[19, 13]
[19, 12]
最短路长度为:33
用时:6ms
上面输出的例如:
[1, 4]
[1, 5]
[1, 6]
的文字代表最短路径(从上往下看):
即从(1,4)点走到(1,5)点,再从(1,5)点走到(1,6)点
相关文章:

【运筹优化】最短路算法之A星算法 + Java代码实现
文章目录 一、A星算法简介二、A星算法思想三、A星算法 java代码四、测试 一、A星算法简介 A*算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。 二、A星算…...
[6]PCB设计实验|认识常用元器件|电阻器|18:30~19:00
目录 一、电阻器主要用途 1. 稳定和调节电路中的电流和电压 2. 作为分流、分压和负载使用 二、常见电阻器 1. 贴片电阻 2. 热敏电阻 3. 限流电阻 4. 可调电阻 5. 排阻(网络电阻) 三、几种常用电阻器的结构特点 四、电阻的参数 1. 额定功率 电阻器功率的表示 2…...
Webots R2021a教程
文章目录 Windows安装设置中文打开世界添加贴图 为外部控制器配置Anaconda解决报错:CondaSSLError: Encountered an SSL error. Most likely a certificate verification issue.调用Python API Windows 安装 进入下载页面 https://github.com/cyberbotics/webots/r…...

C++ 输出格式控制
C 输出格式控制 需包含头文件: 浮点数精度、域宽、填充 操作符功能right-alignedright-alignedsetprecision(int n)设置以n表示的数值精度setw(int n)设置以n表示的域宽setfill(char c)设置以c表示的填充字符 输出格式 操作符功能oct以八进制格式输出数据dec以…...

【C++】引用和右值引用
目录 1. 引用 1.1 引用的概念 1.2 引用的特性 1.3 引用的使用场景 1.3.1 作为参数 1.3.2 作为返回值 1.4 常量引用 1.5 引用和指针的区别 2. 左值和右值 3. 右值引用 3.1 右值引用的概念 3.2 左值持久;右值短暂 3.3 变量是左值 3.4 标准库move函数 1.…...

NodeJS MongoDB⑦
文章目录 ✨文章有误请指正,如果觉得对你有用,请点三连一波,蟹蟹支持😘前言Node&MongoDB 第一步 连接数据库 第二步 创建User Mongodb模型 第三步 简单使用 Mongodb命令 第四步 规范使用 Mongodb命令 (…...
-共现语义篇)
情感分析实战(中文)-共现语义篇
情感分析实战(中文)-共现语义网络分析 背景:该专栏的目的是将自己做了N个情感分析的毕业设计的一个总结版,不仅自己可以在这次总结中,把自己过往的一些经验进行归纳,梳理,巩固自己的知识从而进一步提升,而帮助各大广大学子们,在碰到情感分析的毕业设计时,提供一个好的…...

【数据结构与算法】03 队列(顺序队列--循环队列--优先级队列--链队列)
一、概念1.1 队列的基本概念1.2 队列的顺序存储结构1.21 顺序队列(静态队列)1.22 循环队列1.23 优先级队列 1.3 队列的链式存储结构 二、C语言实现2.1 顺序存储2.11 顺序队列2.12 循环队列2.13 优先级队列 2.2 链式存储 一、概念 1.1 队列的基本概念 队…...

【区块链 | L2】作为Layer2赛道的领跑者,如何理解 Arbitrum?
上周我们介绍了以太坊L2扩展解决方案Optimism,本周我们继续介绍另一个L2解决方案——Arbitrum。Arbitrum 是以太坊的一个 Optimistic Rollup L2 可扩展性解决方案。 Part.1 什么是Arbitrum? Arbitrum 是一个构建在以太坊之上的区块链网络。你可以使用 Arbitrum 链来做任何在…...
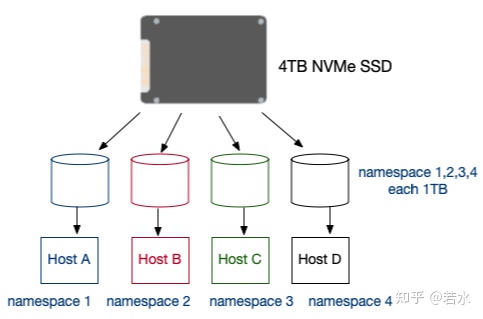
【协议】NVMe over RoCE |nvmeof
什么是nvme nvme ssd和普通ssd区别 ssd是固态硬盘,普通的ssd配的是SATA口(AHCI协议),nvme ssd配的是PCIe口(nvme传输协议) 相比普通SSD的SATA口,nvme的PCIe口有巨大的性能优势。 更多详情见&…...
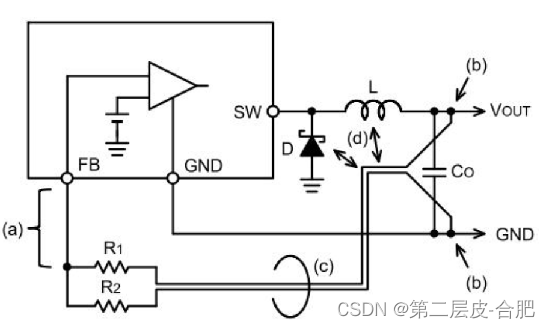
硬件设计电源系列文章-DCDC转换器布局设计
文章目录 概要 整体架构流程 技术名词解释 1.开关电源PCB布局要点 2.输入电容的放置 3.二极管的放置 4.散热孔的放置 5.反馈路径的走线 小结 概要 提示:这里可以添加技术概要 例如: 本文主要DCDC转换器布局方面的知识。 整体架构流程 提示…...

「从入门到精通,一位设计师分享学习Illustrator的技巧和经验!」
学习Illustrator的个人笔记:从入门到精通 Adobe Illustrator是一款广泛使用的矢量图形软件,用于创建各种设计作品,如商标、海报、名片等。在本篇博客中,我将分享学习Illustrator的经验和技巧,帮助您更好地掌握这一工具…...

RedisGraph的整体架构
The architecture of RedisGraph 本文关注RedisGraph的整体架构,分别从图存储模型、索引、并发控制、和执行计划四个方面简要阐述。下图为RedisGraph的整体架构图。 1 图存储模型 了解一个图数据库的架构,最重要的就是其图存储模型,即其中的…...

C#可视化 家用轿车信息查询系统(具体做法及全部代码)
目录 题目: 效果图: 数据库: 做法: combobox值更新 查询按钮功能(非空验证,查询数据) datagirdview设置 全部代码: DBHelper类 From1主窗体代码 题目: 效果图&#…...

Nautilus Chain全球行分享会,上海站圆满举办
在北京时间 6 月 9 日,由 Nautilus Chain 主办的“Layer3 模块化区块链的发展探讨”为主题的全球行活动,在上海顺利举办,本次分享会联合主办方还包 括 Stanford Blockchain Accelerator、Zebec Protocol、Tiger VC DAO、Crypto PHD、Rootz La…...

day50_mybatis
今日内容 0 复习昨日 一、分页插件 二、ORM映射【重点】 三、多表联查 【重点】 四、动态SQL 【重点】 五、$和# 零、复习昨日 mybatis orm框架,作用于持久层,高效开发,只关注sql,其他不用关心 思考MyBatis到底帮你省了哪些事情? jdbc第四步sql自己编写之外,其他mybatis都做了…...

第十一届“创业江苏”科技创业大赛正式启动
为深入实施创新驱动战略, 推进高水平科技自立自强,强化企业创新主体地位,加速推动创新要素向企业集聚,促进科技和金融深度融合,优化科技创新创业生态,吸引优秀创业团队及企业到苏州创新发展,根据…...

EasyX实现简易贪吃蛇
📝个人主页:认真写博客的夏目浅石. 📣系列专栏:夏目的C语言宝藏 文章目录 前言一、头文件包含二、创建蛇与食物的结构体三、游戏的初始化四、游戏的绘画事件五、蛇的移动事件六、输入方向七、生成食物八、吃食物九、游戏失败的判定…...

Linux下ElasticSearch7.9.2安装配置(包含服务器配置、启动停止脚本、开放端口和elasticsearch-head插件的使用)
Linux下ElasticSearch7.9.2安装配置 前言1.下载安装1.1 使用wget的方式下载1.2 官网下载 2.上传到服务器并解压3.修改es配置文件3.1 es目录简介3.2 修改配置文件 4. 创建用户并赋权5. 服务器修改配置5.1 修改文件句柄数和线程数5.2 关闭swapping5.3 修改虚拟内存 6. 启动es6.1 …...

JS 之 事件Event对象详解(属性、方法、自定义事件)
一、Event对象 1、简介 事件event对象是指在浏览器中触发事件时,浏览器会自动创建一个event对象,其中存储了本次事件相关的信息,包括事件类型、事件目标、触发元素等等。浏览器创建完event对象之后,会自动将该对象作为参数传…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
