贪心算法part2 | ● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录
- 122.买卖股票的最佳时机II
- 思路
- 思路代码
- 官方题解
- 困难
- 55. 跳跃游戏
- 思路
- 思路代码
- 官方题解
- 代码
- 困难
- 45.跳跃游戏II
- 思路
- 思路代码
- 困难
- 今日收获
122.买卖股票的最佳时机II
122.买卖股票的最佳时机II
思路
局部最优:将当天价格和前一天比较,价格涨了就买入,价格降了就忽略。
思路代码
func maxProfit(prices []int) int {res:=0pre:=prices[0]for i:=1;i<len(prices);i++{if prices[i]>pre{res+=(prices[i]-pre)}pre=prices[i]}return res
}
官方题解
官方亦是如此。
困难
不需要第一天,所以循环从第二天也就是1开始。
55. 跳跃游戏
55.跳跃游戏
思路
局部最优:每次选取能覆盖的最大范围,说明范围以内的
思路代码
func canJump(nums []int) bool {cover:=0for i:=0;i<len(nums);i++{for j:=i;j<=cover;j++{if cover<i+nums[i]{cover=i+nums[i]}if cover>=len(nums)-1{return true}}}return false
}
官方题解
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
局部最优推出全局最优,找不出反例
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
如果 cover 大于等于了终点下标,直接 return true 就可以了。
一个循环,时间复杂度更优。
代码
func canJump(nums []int) bool {cover := 0n := len(nums)-1for i := 0; i <= cover; i++ { // 每次与覆盖值比较cover = max(i+nums[i], cover) //每走一步都将 cover 更新为最大值if cover >= n {return true}}return false
}
func max(a, b int ) int {if a > b {return a}return b
}
困难
让i每次只能在cover内移动,每次循环实时更新cover的值,也就是循环的范围在循环的同时就可以扩大,不需要两层循环。
45.跳跃游戏II
45.跳跃游戏II
思路
记录下一步的覆盖范围
局部最优:走到当前覆盖范围后步数加一并更新当前覆盖范围。(每一步都走到最远)
思路代码
func jump(nums []int) int {cover:=0res:=0nextcover:=0for i:=0;i<len(nums)-1;i++{if nextcover<nums[i]+i{nextcover=nums[i]+i}if i==cover{res++cover=nextcover}}return res
}
困难
优化后只需要走到倒数第二个位置即可。因为题目说必定能到达终点。
今日收获
对贪心算法的局部最优有了更深的认识。
例如跳跃问题这种每次更新范围的问题,使用一个循环,贪心找到每一步覆盖的最大范围。
相关文章:

贪心算法part2 | ● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录 122.买卖股票的最佳时机II思路思路代码官方题解困难 55. 跳跃游戏思路思路代码官方题解代码困难 45.跳跃游戏II思路思路代码困难 今日收获 122.买卖股票的最佳时机II 122.买卖股票的最佳时机II 思路 局部最优:将当天价格和前一天比较,价格涨…...

[C++]异常笔记
我不怕练过一万种腿法的对手,就怕将一种腿法 练一万次的对手。 什么是C的异常 在C中,异常处理通常使用try-catch块来实现。try块用于包含可能会抛出异常的代码,而catch块用于捕获并处理异常。当异常被抛出时,程序会跳过try块中未执行…...

浅谈一级机电管道设计中的压力与介质温度
管道设计是工程设计中的一个非常重要的部分,管道的设计需要考虑到许多因素,其中就包括管道设计压力分类和介质温度分类。这两个因素是在设计管道时必须非常严格考虑的, 首先是管道设计压力分类。在管道设计中,根据工作要求和要传输…...
使用 macvlan 网络)
Docker网络模型(八)使用 macvlan 网络
使用 macvlan 网络 一些应用程序,特别是传统的应用程序或监控网络流量的应用程序,期望直接连接到物理网络。在这种情况下,你可以使用 macvlan 网络驱动为每个容器的虚拟网络接口分配一个MAC地址,使其看起来像一个直接连接到物理网…...
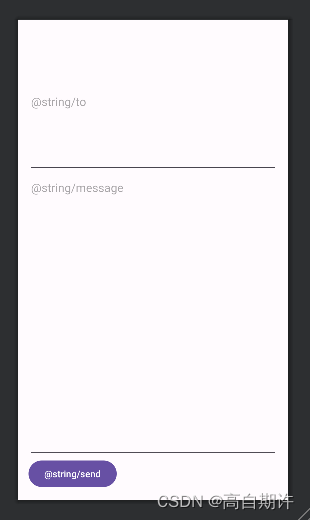
控制视图内容的位置
文本域中的提示内容在默认情况下是垂直居中的,要改变文本在文本域中的位置,可以使用android:gravity来实现。 利用android:gravity可以指定如何在视图中放置视图内容,例如,如何在文本域中放置文本。 如果希望视图文本显示在上方&a…...

【分布式系统与一致性协议】
分布式系统与一致性协议 CAP原理APCPCA总结BASE理论 一致性拜占庭将军问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 分布式系统的设计目标一般包含如下: 可用性:可用性是分…...

音视频领域的未来发展方向展望
文章目录 音视频领域的未来发展方向全景音视频技术虚拟现实和增强现实的区别 人工智能技术可视化智能分析智能语音交互图像识别和视频分析技术 语音处理智能推荐技术远程实时通信 流媒体技术未来方向 音视频领域的未来发展方向 全景音视频技术:全景音视频技术是近年…...
时间同步/集群时间同步/在线/离线
目录 一、能够连接外网 二、集群不能连接外网--同步其它服务器时间 一、能够连接外网 1.介绍ntp时间协议 NTP(Network Time Protocol)网络时间协议,是用来使计算机时间同步的一种协议,它可以使计算机对其服务器或时钟源做同步…...
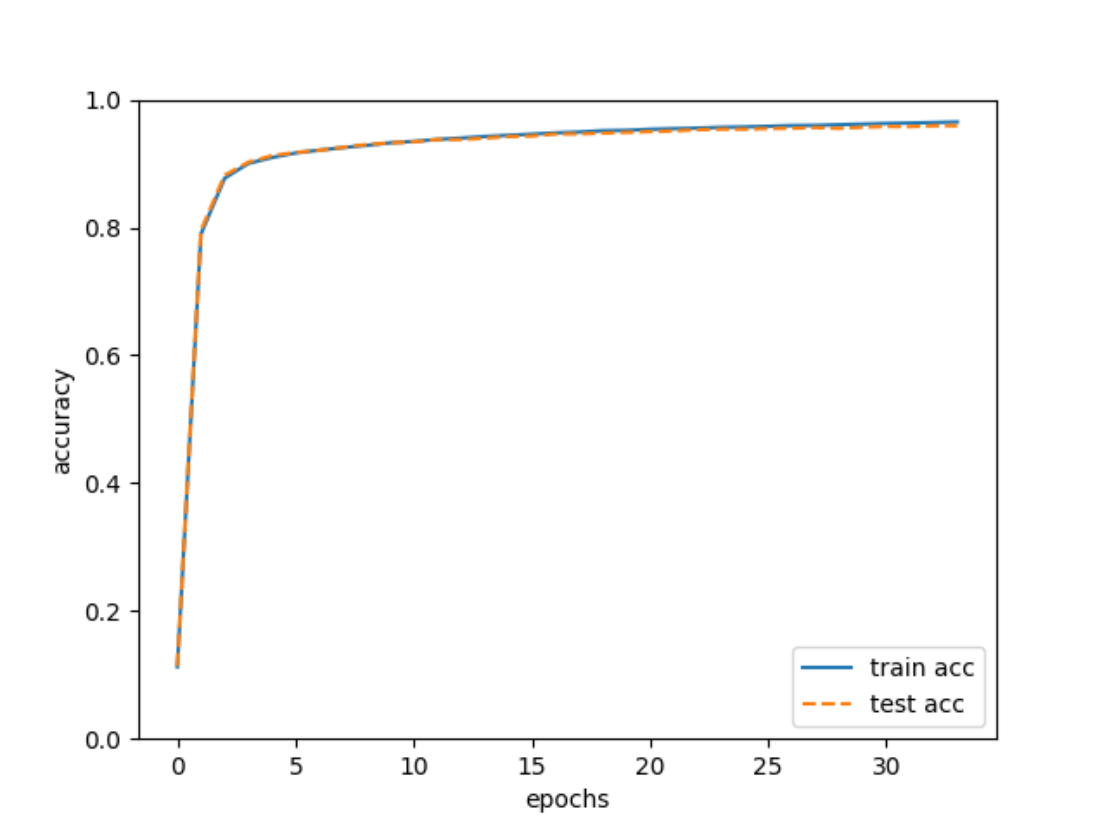
基于BP神经网络对MNIST数据集检测识别(numpy版本)
基于BP神经网络对MNIST数据集检测识别 1.作者介绍2.BP神经网络介绍2.1 BP神经网络 3.BP神经网络对MNIST数据集检测实验3.1 读取数据集3.2 前向传播3.3 损失函数3.4 构建神经网络3.5 训练3.6 模型推理 4.完整代码 1.作者…...
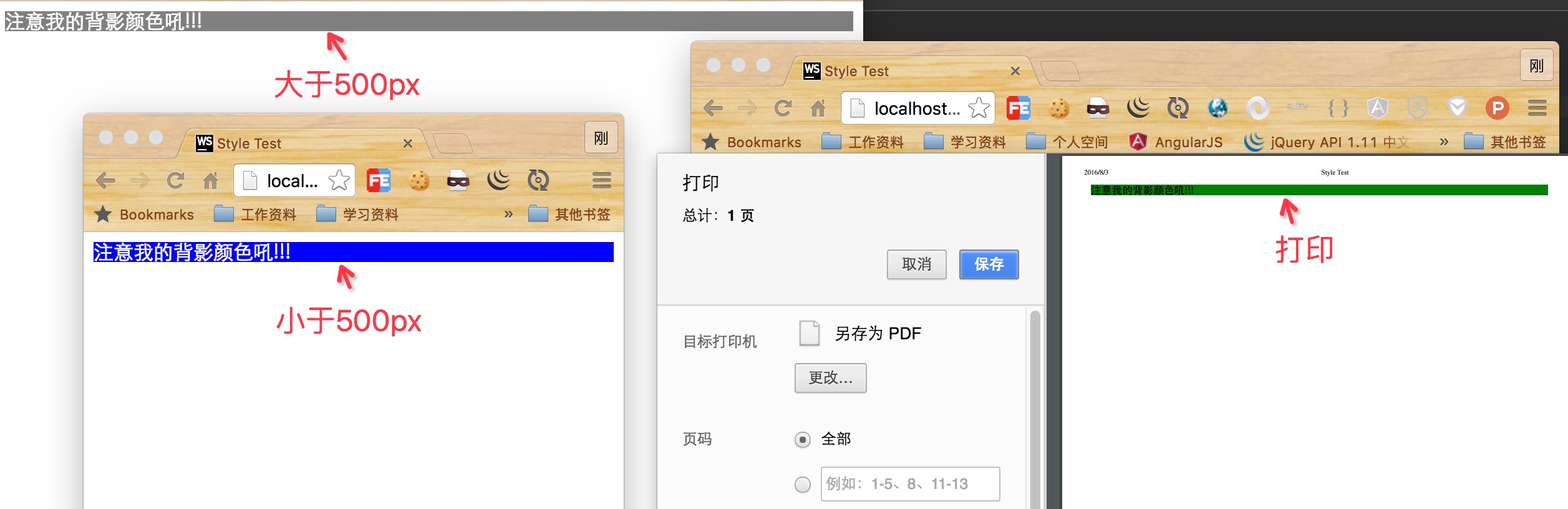
HTML5-创建HTML文档
HTML5中的一个主要变化是:将元素的语义与元素对其内容呈现结果的影响分开。从原理上讲这合乎情理。HTML元素负责文档内容的结构和含义,内容的呈现则由应用于元素上的CSS样式控制。下面介绍最基础的HTML元素:文档元素和元数据元素。 一、构建…...

Vue中Axios的封装和API接口的管理
一、axios的封装 在vue项目中,和后台交互获取数据这块,我们通常使用的是axios库,它是基于promise的http库,可运行在浏览器端和node.js中。他有很多优秀的特性,例如拦截请求和响应、取消请求、转换json、客户端防御XSR…...

MLIR面试题
1、请简要解释MLIR的概念和用途,并说明MLIR在编译器领域中的重要性。 MLIR(Multi-Level Intermediate Representation)是一种多级中间表示语言,提供灵活、可扩展和可优化的编译器基础设施。MLIR的主要目标是为不同的编程语言、领域专用语言(DSL)和编译器…...
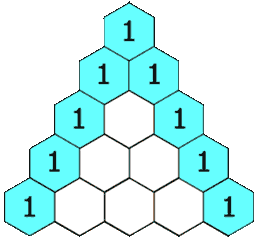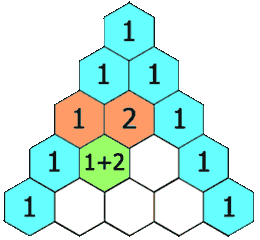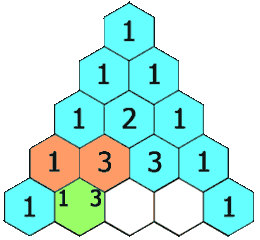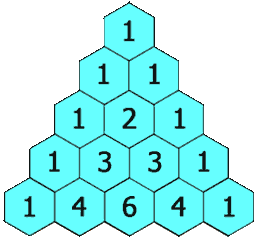
***杨辉三角_yyds_LeetCode_python***
1.题目描述: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] 示例 2: 输入: numRows …...
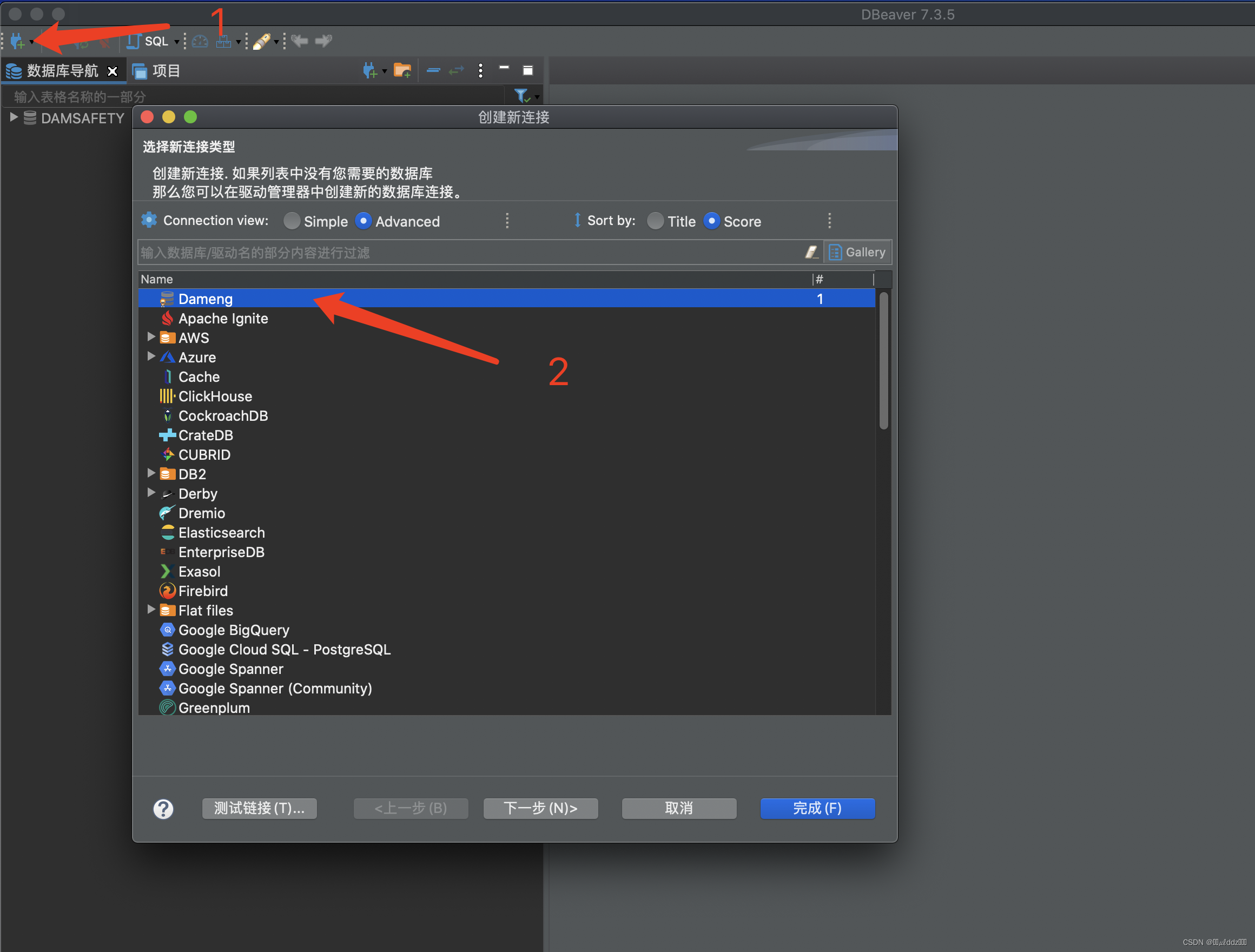
Mac使用DBeaver连接达梦数据库
Mac使用DBeaver连接达梦数据库 下载达梦驱动包 达梦数据库 在下载页面随便选择一个系统并下载下来。 下载下来的是zip的压缩包解压出来就是一个ISO文件,然后我们打开ISO文件进入目录:/dameng/source/drivers/jdbc 进入目录后找到这几个驱动包&#x…...

spring.expression 随笔0 概述
0. 我只是个普通码农,不值得挽留 Spring SpEL表达式的使用 常见的应用场景:分布式锁的切面借助SpEL来构建key 比较另类的的应用场景:动态校验 个人感觉可以用作控制程序的走向,除此之外,spring的一些模块的自动配置类,也会在Cond…...

从Cookie到Session: Servlet API中的会话管理详解
文章目录 一. Cookie与Session1. Cookie与Session2. Servlet会话管理操作 二. 登录逻辑的实现 一. Cookie与Session 1. Cookie与Session 首先, 在学习过 HTTP 协议的基础上, 我们需要知道 Cookie 是 HTTP 请求报头中的一个关键字段, 本质上是浏览器在本地存储数据的一种机制,…...
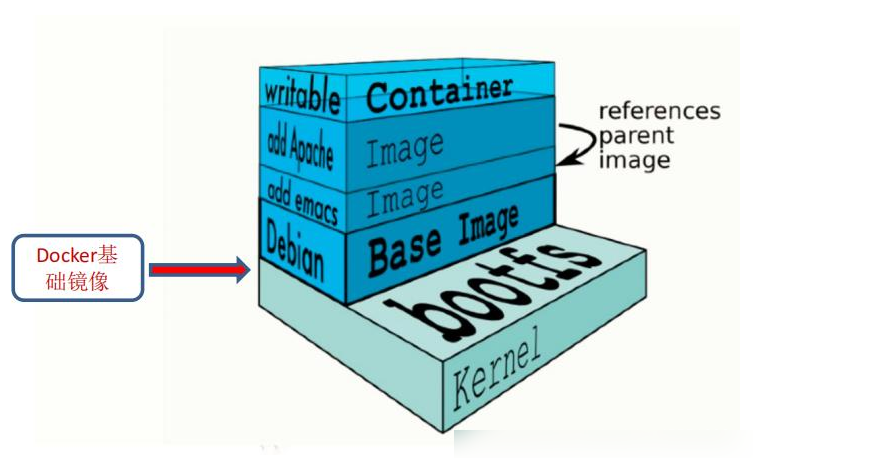
docker数据管理与网络通信
一、管理docker容器中数据 管理Docker 容器中数据主要有两种方式:数据卷(Data Volumes)和数据卷容器( DataVolumes Containers) 。 1、 数据卷 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机的目录挂载到数据卷上,对数据卷的修改操作立刻…...
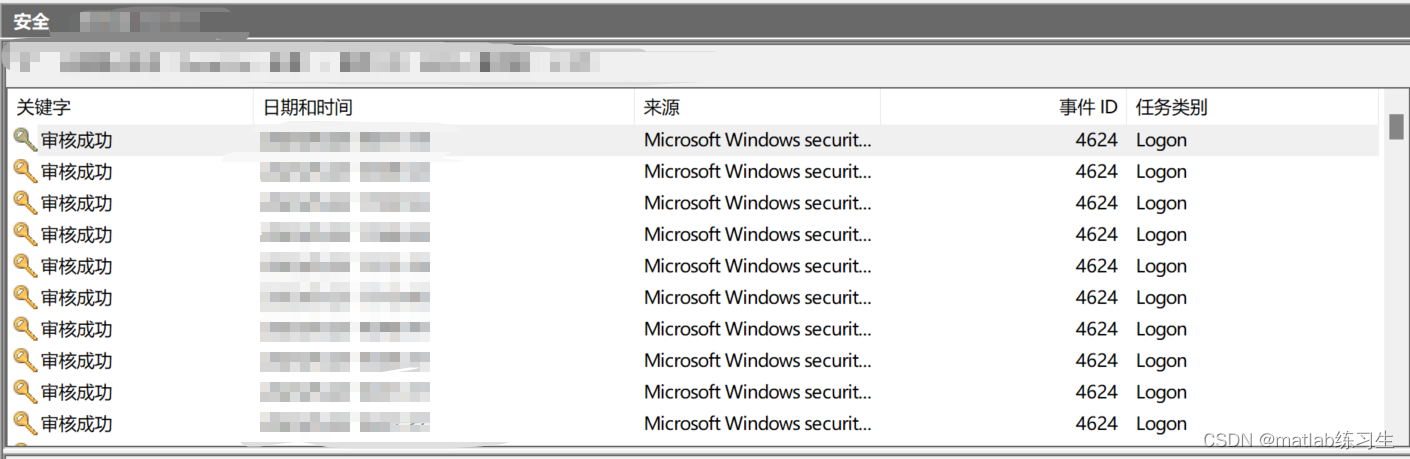
怎么查询电脑的登录记录及密码更改情况?
源头是办公室公用的电脑莫名其妙打不开了,问别人也都不知道密码是多少 因为本来就没设密码啊!(躺倒) 甚至已经想好了如果是50万想攻破电脑,被po抓住要怎么花这笔钱了 是我想太多 当然最后也没解决,莫名…...
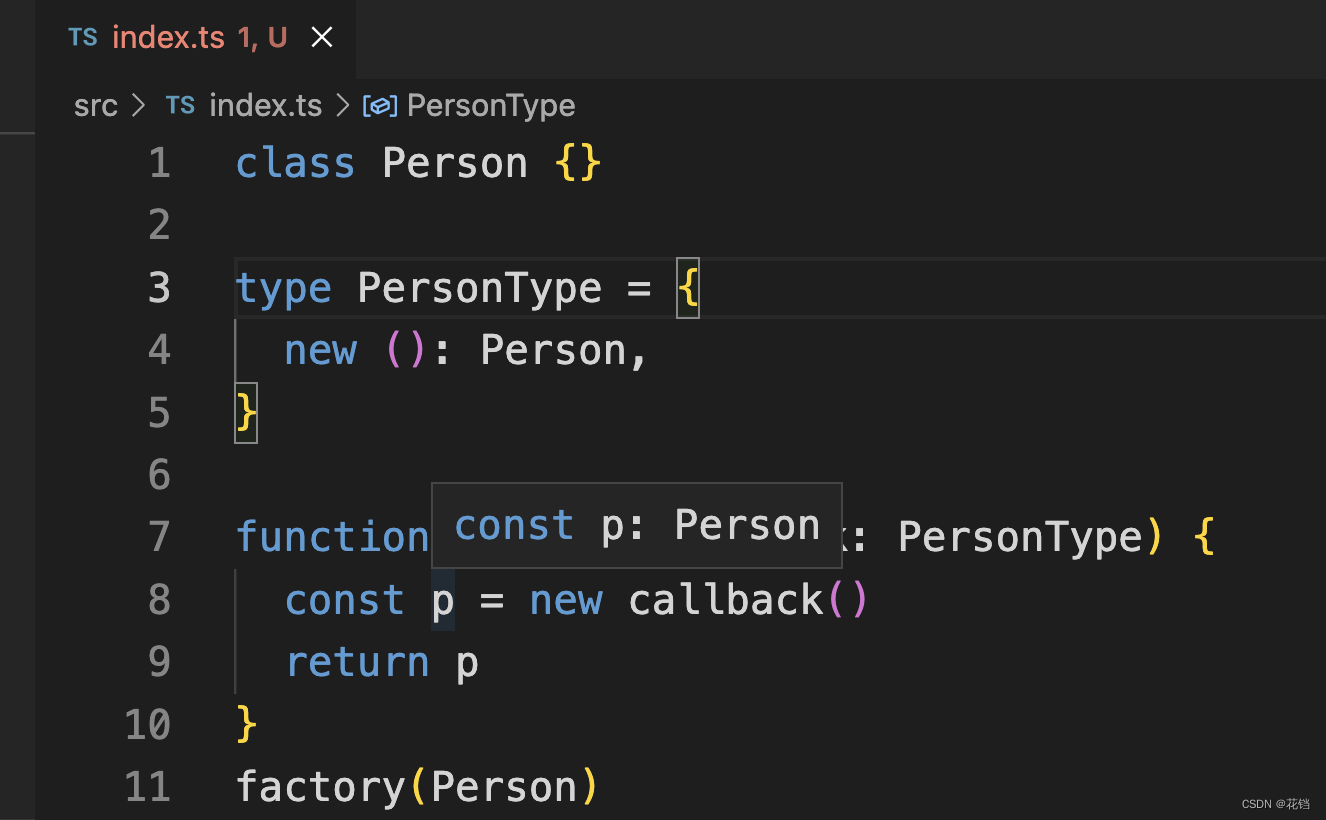
《三》TypeScript 中函数的类型
TypeScript 允许指定函数的参数和返回值的类型。 函数声明的类型定义:function 函数名(形参: 形参类型, 形参: 形参类型, ...): 返回值类型 {} function sum(x: number, y: number): number {return x y } sum(1, 2) // 正确 sum(1, 2, 3) // 错误。输入多余的或者…...
深入学习 Mysql 引擎 InnoDB、MyISAM
tip:作为程序员一定学习编程之道,一定要对代码的编写有追求,不能实现就完事了。我们应该让自己写的代码更加优雅,即使这会费时费力。 💕💕 推荐:体系化学习Java(Java面试专题&#…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
