2023蓝桥杯大学A组C++决赛游记+个人题解
Day0
发烧了一晚上没睡着,感觉鼻子被打火机烧烤一样难受,心情烦躁
早上6点起来吃了个早饭,思考能力完全丧失了,开始看此花亭奇谭
看了六集,准备复习数据结构考试,然后秒睡
一睁眼就是下午2点了
挂了个毛概课串讲,点了个外卖,吃完又睡着了
醒来就晚上8点了
然后又点了个外卖,复习了三章数据结构
就凌晨2点了,睡觉
Day1
7:40醒,被催着上了车,精神恍惚
然后开始考试
第一题
第一题就被难到了
分割圆形,以为是卡特兰数,但又觉得不一样
不给样例,题意也不是很清楚啊。。。
随便推了推
首先,连接相邻两个点的边(外圈)肯定得单独拿出来考虑,也就是2^n种外圈情况
然后设f[n]表示n边形内部划线不相交的方案数
简单推推得到f[n]=2*f[n-1]+Σf[i+1]*f[n-i+1]
f[3]=1;f[4]=3;.........
也不知道对不对,反正这么写了
最后好像是1392(可能是错的)
第二题
求2^(3^(4^(……^2023)))%2023
扩展欧拉定理
没什么好说的,背不到公式了
(翻了翻以前的博客)
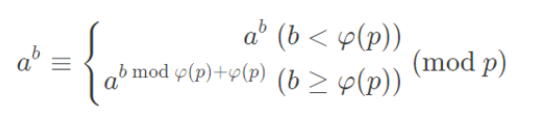
emm……犯了一个扩展欧拉定理的典型错误
没加phi(p)
所以答案好像是869?
后面补的代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int gcd(int x,int y){return !y?x:gcd(y,x%y);}
int phi(int n)
{int sum=0;for(int i=1;i<n;i++)if(gcd(i,n)==1)sum++;return sum;
}
int ksm(int x,int y,int m)
{int ret=1;while(y){if(y&1)ret=1ll*ret*x%m;x=1ll*x*x%m;y>>=1;}return ret;
}
int minksm(int x,int y,int m)
{int ret=1;while(y){if(y&1)ret=min(1ll*ret*x,1ll*m);x=min(1ll*x*x,1ll*m);y>>=1;}return ret;
}
const int mod=2023;
pair<int,bool> f(int n,int m)
{if(m==1)return pair(1,1);pair<int,int> p=f(n+1,phi(m));int b=p.first;if(p.second) b+=phi(m);printf("%d^%d\n",n,b);if(minksm(n,b,m)==m)return pair(ksm(n,b,m),1);return pair(ksm(n,b,m),0);
}
int main()
{printf("%d",f(2,2023).first);
}(所以搞了40分钟填空题是一分没得是吧)
第三题
把长方形分割成小正方形,让小正方形的数量最多
寻找大于2的最小公因数(没错是最小)
然后直接除一除就结束了
第四题
给出L,R
求x+y=z算式的数目(L<=x,y,z<=R)
数学题,稍微推一推就好
这题极度阴间,小心爆你的longlong(针对某些特定的写法)
第五题
第K小的和
给两个数组A,B。
从A、B中各选一个数加起来,组成C数组,求C数组中第K小的数。
二分答案+two-pointers,注意边界条件的验证
第六题
相连的边
给出一棵带权树,选择相连的三条边,让他们的边权和最大。
首先这三条边只可能是一条链,或者是菊花图
菊花图直接对每个点的相连的边排序
把树定根后,链的情况分两种,一种是直链,一种是有LCA的链
直链的情况直接枚举每个点,向上走三步统计边权
有LCA的情况,其实是两种直链的情况加起来,一边直链长度是2,另一边是1
枚举长度为2的直链,即枚举每个点向上走两步,然后在爷爷节点选择除去走上来的边的最大邻接边即可
注意细节处理。
第七题
01游戏
题目保证有解
直接爆搜
剪枝很多,横竖相连三个不能相同,每行的01个数不超过一半,算完每行每列用二进制val值去重
从11点10写到11点40
最后时间10*10的全下划线不到0.5s
第八题
求一个字符串中长度为i的本质不同的子串的个数(i=1~n)
应该是SAM板题,可惜我背不到了,老了啊┭┮﹏┭┮
写了个双哈希n^2logn,能过4000都顶天了
第九题
求一棵树中距离为i的简单路径条数(i=L~R)
点分治板题,可惜我背不到了,老了老了
暴力n^2走人,居然还有40%
md,lqb出题这么这个样子???尽是出板题是吧???欺负我退役多年的老同志
第十题
本来只剩20分钟了,想着暴力也不是很好写,于是想了想正解,发现正解不难
状压DP,SPFA型转移
f[u][S][hp]表示当前在点u,存在怪兽的点的状态为S,当前血量为hp
很显然
(u,v)存在时:
if(S&(1<<v))
f[v][S-(1<<v)][hp-cal(S,v)]=min(f[u][S][hp]+w(u,v))
else
f[v][S][hp]=min(f[u][S][hp]+w(u,v))
然后就利用SPFA转移
最后答案应该是max(f[n-1][……][1~HP])
最后没写完,哪怕前面填空题不做也好啊,最后留个10~20分钟就搞定了,太菜了
总结
总之就是非常菜,简单题背不到公式,板题背不到板子,题目都写不完,太菜了。
相关文章:
2023蓝桥杯大学A组C++决赛游记+个人题解
Day0 发烧了一晚上没睡着,感觉鼻子被打火机烧烤一样难受,心情烦躁 早上6点起来吃了个早饭,思考能力完全丧失了,开始看此花亭奇谭 看了六集,准备复习数据结构考试,然后秒睡 一睁眼就是下午2点了 挂了个…...

wkhtmltopdf踩坑记录
1. 不支持writing-mode。 需求是文字纵向排列,内容从左到右,本来用的是writing-mode: tb-rl;,插件转pdf后发现失效。 解决方法: 让每一列文字单独用一个div容器包裹,对它的宽度进行限制,控制每一行只能出现…...

贪心算法part2 | ● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录 122.买卖股票的最佳时机II思路思路代码官方题解困难 55. 跳跃游戏思路思路代码官方题解代码困难 45.跳跃游戏II思路思路代码困难 今日收获 122.买卖股票的最佳时机II 122.买卖股票的最佳时机II 思路 局部最优:将当天价格和前一天比较,价格涨…...

[C++]异常笔记
我不怕练过一万种腿法的对手,就怕将一种腿法 练一万次的对手。 什么是C的异常 在C中,异常处理通常使用try-catch块来实现。try块用于包含可能会抛出异常的代码,而catch块用于捕获并处理异常。当异常被抛出时,程序会跳过try块中未执行…...

浅谈一级机电管道设计中的压力与介质温度
管道设计是工程设计中的一个非常重要的部分,管道的设计需要考虑到许多因素,其中就包括管道设计压力分类和介质温度分类。这两个因素是在设计管道时必须非常严格考虑的, 首先是管道设计压力分类。在管道设计中,根据工作要求和要传输…...
使用 macvlan 网络)
Docker网络模型(八)使用 macvlan 网络
使用 macvlan 网络 一些应用程序,特别是传统的应用程序或监控网络流量的应用程序,期望直接连接到物理网络。在这种情况下,你可以使用 macvlan 网络驱动为每个容器的虚拟网络接口分配一个MAC地址,使其看起来像一个直接连接到物理网…...
控制视图内容的位置
文本域中的提示内容在默认情况下是垂直居中的,要改变文本在文本域中的位置,可以使用android:gravity来实现。 利用android:gravity可以指定如何在视图中放置视图内容,例如,如何在文本域中放置文本。 如果希望视图文本显示在上方&a…...

【分布式系统与一致性协议】
分布式系统与一致性协议 CAP原理APCPCA总结BASE理论 一致性拜占庭将军问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 分布式系统的设计目标一般包含如下: 可用性:可用性是分…...

音视频领域的未来发展方向展望
文章目录 音视频领域的未来发展方向全景音视频技术虚拟现实和增强现实的区别 人工智能技术可视化智能分析智能语音交互图像识别和视频分析技术 语音处理智能推荐技术远程实时通信 流媒体技术未来方向 音视频领域的未来发展方向 全景音视频技术:全景音视频技术是近年…...
时间同步/集群时间同步/在线/离线
目录 一、能够连接外网 二、集群不能连接外网--同步其它服务器时间 一、能够连接外网 1.介绍ntp时间协议 NTP(Network Time Protocol)网络时间协议,是用来使计算机时间同步的一种协议,它可以使计算机对其服务器或时钟源做同步…...
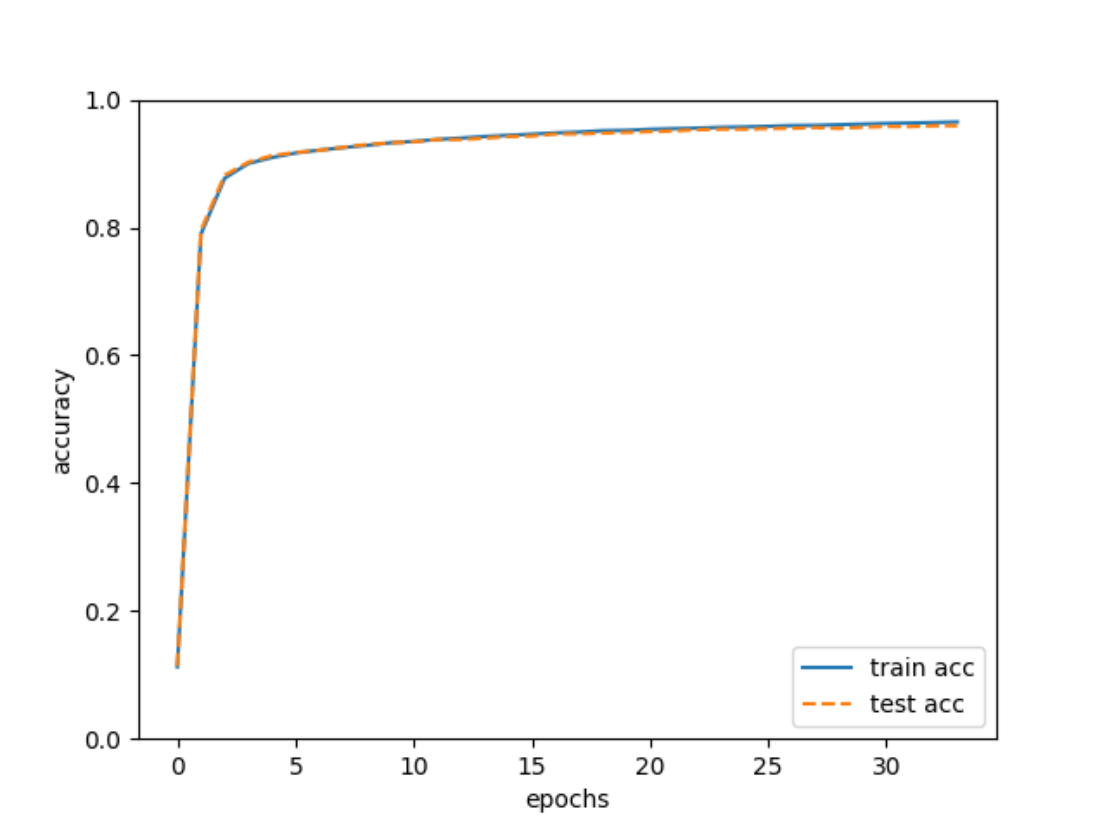
基于BP神经网络对MNIST数据集检测识别(numpy版本)
基于BP神经网络对MNIST数据集检测识别 1.作者介绍2.BP神经网络介绍2.1 BP神经网络 3.BP神经网络对MNIST数据集检测实验3.1 读取数据集3.2 前向传播3.3 损失函数3.4 构建神经网络3.5 训练3.6 模型推理 4.完整代码 1.作者…...
HTML5-创建HTML文档
HTML5中的一个主要变化是:将元素的语义与元素对其内容呈现结果的影响分开。从原理上讲这合乎情理。HTML元素负责文档内容的结构和含义,内容的呈现则由应用于元素上的CSS样式控制。下面介绍最基础的HTML元素:文档元素和元数据元素。 一、构建…...

Vue中Axios的封装和API接口的管理
一、axios的封装 在vue项目中,和后台交互获取数据这块,我们通常使用的是axios库,它是基于promise的http库,可运行在浏览器端和node.js中。他有很多优秀的特性,例如拦截请求和响应、取消请求、转换json、客户端防御XSR…...

MLIR面试题
1、请简要解释MLIR的概念和用途,并说明MLIR在编译器领域中的重要性。 MLIR(Multi-Level Intermediate Representation)是一种多级中间表示语言,提供灵活、可扩展和可优化的编译器基础设施。MLIR的主要目标是为不同的编程语言、领域专用语言(DSL)和编译器…...
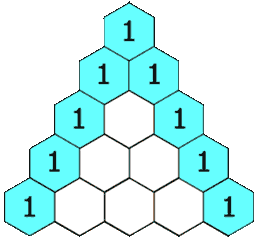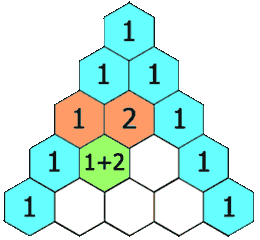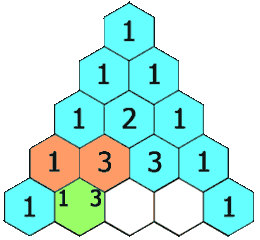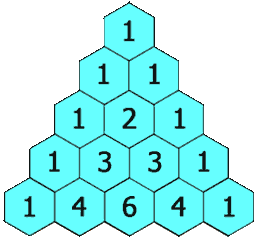
***杨辉三角_yyds_LeetCode_python***
1.题目描述: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] 示例 2: 输入: numRows …...
Mac使用DBeaver连接达梦数据库
Mac使用DBeaver连接达梦数据库 下载达梦驱动包 达梦数据库 在下载页面随便选择一个系统并下载下来。 下载下来的是zip的压缩包解压出来就是一个ISO文件,然后我们打开ISO文件进入目录:/dameng/source/drivers/jdbc 进入目录后找到这几个驱动包&#x…...

spring.expression 随笔0 概述
0. 我只是个普通码农,不值得挽留 Spring SpEL表达式的使用 常见的应用场景:分布式锁的切面借助SpEL来构建key 比较另类的的应用场景:动态校验 个人感觉可以用作控制程序的走向,除此之外,spring的一些模块的自动配置类,也会在Cond…...

从Cookie到Session: Servlet API中的会话管理详解
文章目录 一. Cookie与Session1. Cookie与Session2. Servlet会话管理操作 二. 登录逻辑的实现 一. Cookie与Session 1. Cookie与Session 首先, 在学习过 HTTP 协议的基础上, 我们需要知道 Cookie 是 HTTP 请求报头中的一个关键字段, 本质上是浏览器在本地存储数据的一种机制,…...
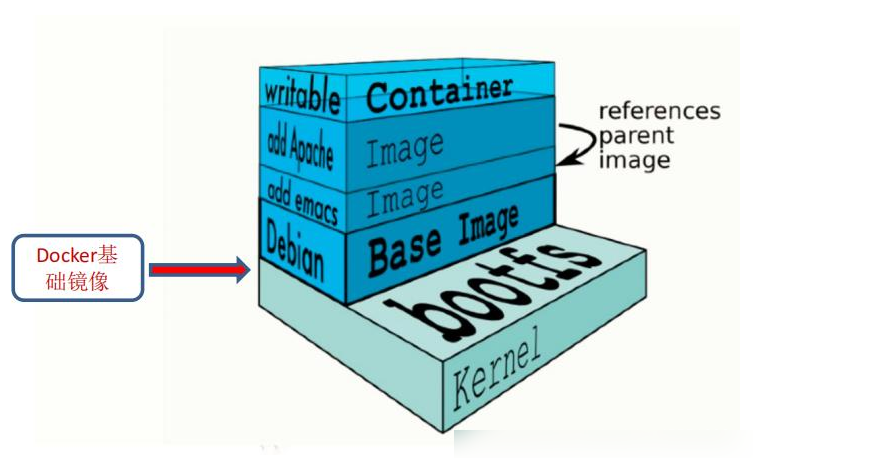
docker数据管理与网络通信
一、管理docker容器中数据 管理Docker 容器中数据主要有两种方式:数据卷(Data Volumes)和数据卷容器( DataVolumes Containers) 。 1、 数据卷 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机的目录挂载到数据卷上,对数据卷的修改操作立刻…...
怎么查询电脑的登录记录及密码更改情况?
源头是办公室公用的电脑莫名其妙打不开了,问别人也都不知道密码是多少 因为本来就没设密码啊!(躺倒) 甚至已经想好了如果是50万想攻破电脑,被po抓住要怎么花这笔钱了 是我想太多 当然最后也没解决,莫名…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
