【伏羲八卦图】(PythonMatlab实现)
目录
1 与达尔文对话
2 与老子对话
2.1 Python实现
2.2 Matlab实现
1 与达尔文对话
140年前,1858年7月1日,达尔文在英伦岛发表了自己有关自然选择的杰出论文。他提出,生物的发展规律是物竞天择。经过物竞,自然界选择并存留最具生命优势的物种。这些物种愈竞愈强。直至人,已无所不能,成为统治世界的物种,这已是不争的事实。但在地球的漫长的演化史上,我们又看见,曾经统治地球的庞然大物恐龙消亡了。一-些科学家将其归之于小行星对地球的撞击。但就在我们这一代人眼前,兽中之王的老虎正在一天天消失。我们知道,在其消亡的时间轴上,小行星并未与地球碰撞。


循着达尔文的思索,我们得知:动物强于植物,老虎强于小鼠。愈是后续的物种愈强,因为它们是物竞天择的结果。强者存留,弱者淘汰。但环顾四野,植物茂盛,小鼠成群,而百兽之王的老虎却在一天天消亡。
进一步看,诞生于35亿年以前的最原始的物种单细胞生物,迄今仍然是地球上生存力度最强、生物质量最大、分布范围最广的生命形态,反而是那些在进化史上较晚近的高级物种如哺乳类动物正在以最快的速度灭绝。换一个眼光重新审视考古生物学,我们会发现,在亿万年来已遭灭绝的99%以上的生物品杀里,愈进化的物种淘汰几率愈高、绝种速度愈快,亦即生存力度愈低。
何以是“强”者消亡,“弱”者长存?即是说,在“物竞天择,适者生存”的表观现象后面,实际上暗藏着一个“自然选择偏偏要把最不适于生存的弱化产物层层推出”的单向度规定。印度诗圣泰戈尔说:“我们把世界看错了,反说世界欺骗了我们。”是伟大的达尔文错了,还是世界在我们有限的认知力之外,另有一番规律?
历代的哲人、物理学家、化学家、生物学家、社会学家,或思索过这一问题而不得其解,或已走到这一问题的门口,束手无策而返。其留下的大量艰涩难懂之文,多与此有关。


2 与老子对话
2.1 Python实现
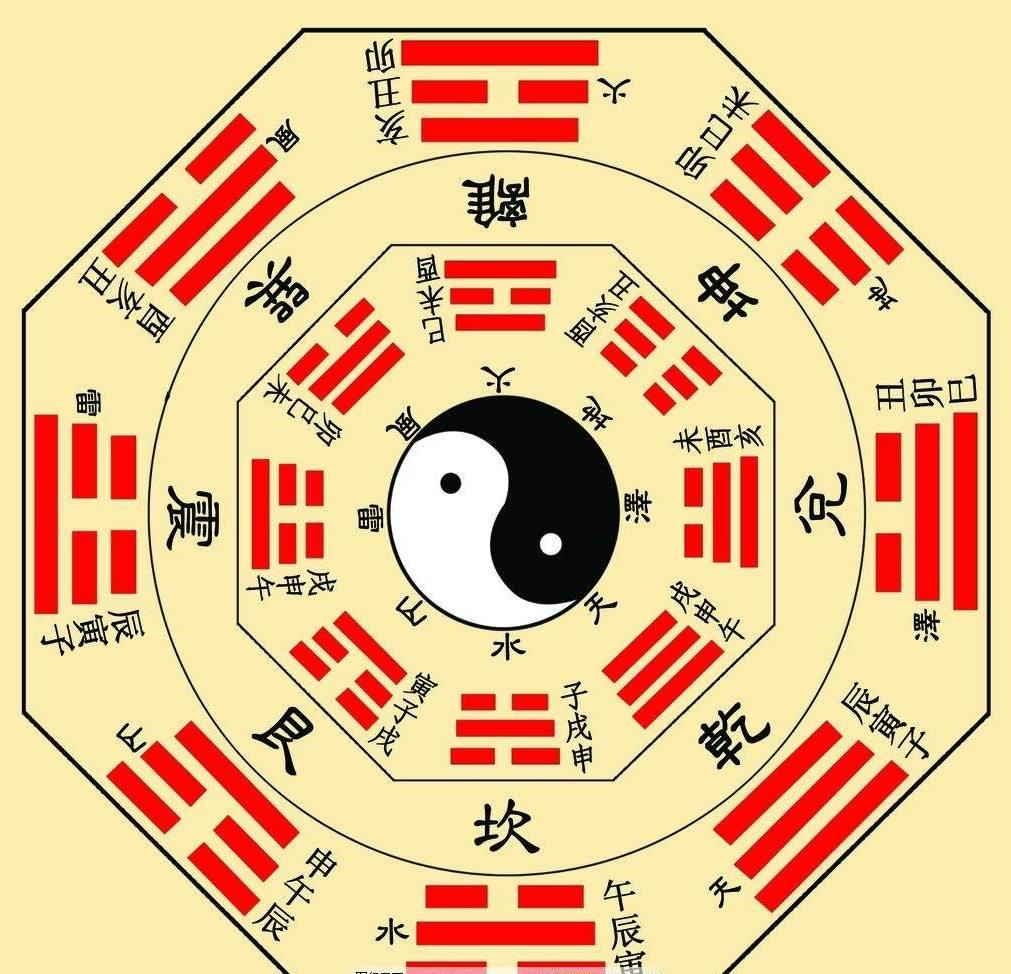

#====导入相关库========
import turtle
import time#====欢迎关注公众号:电力系统与算法之美======
#====更多惊喜,更多浪漫,更多算法等你=====
angle = 270
turtle.title('我与老子对话')
#=====太极图=======
def tai():r = 200 # 设置半径turtle.penup() # 拿起画笔turtle.goto(0, 0) # 到画布中心turtle.setheading(angle) # 设置当前朝向为angle角度turtle.fd(r) # 前进r的距离turtle.pendown() # 放下画笔turtle.right(90) # 调整海龟角度#======画阳鱼======turtle.fillcolor("white") # 填充为白色turtle.begin_fill() # 开始填充turtle.circle(-r / 2, 180)turtle.circle(r / 2, 180)turtle.circle(r, 180)turtle.end_fill() # 填充结束#=====画阴鱼=========turtle.fillcolor("black") # 填充为黑色turtle.begin_fill()turtle.circle(r, 180)turtle.right(180)turtle.circle(-r / 2, 180)turtle.circle(r / 2, 180)turtle.end_fill()#=======画阴鱼眼==========turtle.penup()turtle.setheading(angle)turtle.fd(-r / 2)turtle.pendown()turtle.dot(r / 4, "white") # dot()绘制具有特定大小和颜色的圆点#=========画阳鱼眼=========turtle.penup()turtle.fd(-r)turtle.pendown()turtle.dot(r / 4, "black")turtle.penup()turtle.tracer(0) # 将刷新率置为0,即不刷新
for i in range(10000): # 这里设置了1w次,也可以是其他次数tai()turtle.update() # 更新绘图time.sleep(0.01) # 休眠时间,这一句可以没有,但是如果没有的话,太极转的会很快turtle.clear() # 清空画布angle += 1
2.2 Matlab实现


%% 太极八卦图%%~~~~~~~欢迎关注公众号:电力系统与算法之美~~~~%%clc;clear;close all;
t=0:.1:pi;
T=0:.1:2*pi;
c=@(t)cos(t);s=@(t)sin(t);
x=c(t);y=s(t);
X=c(t);Y=s(-t);
x1=.1*c(T)-.5;y1=.1*s(T);
x2=x1+1;%y2=y1;
x3=.5*c(t)-.5;y3=.5*s(t);
x4=x3+1;%y4=-y3;
hold on
f=@(x,y,c)fill([x,flip(x3,2),flip(x4,2)],...[y,flip(y3,2),flip(-y3,2)],c);
f(X,Y,'k');
f(x,y,'w');
fill(x2,y1,'k',x1,y1,'w')
axis square off
相关文章:

【伏羲八卦图】(PythonMatlab实现)
目录 1 与达尔文对话 2 与老子对话 2.1 Python实现 2.2 Matlab实现 1 与达尔文对话 140年前,1858年7月1日,达尔文在英伦岛发表了自己有关自然选择的杰出论文。他提出,生物的发展规律是物竞天择。经过物竞,自然界选择并存留最具…...

ruoyi数据权限学习
思路 用户关联了角色(用户可以关联多个角色),给角色设置数据权限分类,数据权限分类有如下5种: 全部数据权限 - DATA_SCOPE_ALL自定数据权限 - DATA_SCOPE_CUSTOM部门数据权限 - DATA_SCOPE_DEPT部门及以下数据权限 -…...

WPF中实现动态导航
主页面 <mah:MetroWindowx:Class"Kx.View.MyMainView"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expression/bl…...

day16 | 104.二叉树的最大深度、111.二叉树的最小深度、 222.完全二叉树的节点个数
目录: 链接 题目链接: https://leetcode.cn/problems/maximum-depth-of-binary-tree/ https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/ https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/ 解题及思路学习 104…...

Spring Boot + Vue3前后端分离实战wiki知识库系统<八>--分类管理功能开发二
接着上一次Spring Boot Vue3 前后端分离 实战 wiki 知识库系统<七>--分类管理功能开发的分类功能继续完善。 分类编辑功能优化: 概述: 现在分类编辑时的界面长这样: 很明显目前的父分类的展现形式不太人性…...
类(一))
Python入门(十八)类(一)
类(一) 1.面向对象概述2.创建和使用类2.1 创建dog类2.2 根据类创建实例2.3 创建多个实例 1.面向对象概述 面向对象编程是最有效的软件编写方法之一。在面向对象编程中,你编写表示现实世界中的事物和情景的类,并基于这些类来创建对…...

c# 从零到精通-定义一个结构
c# 从零到精通-定义一个结构 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Test01 { class Program { public struct Rect//定义一个矩形结构 { public double width;//矩形的宽 public double height;//矩形的高 /// …...

检信ALLEMOTION非接触式心理情绪测评系统
1 名称:检信ALLEMOTION多维度心理情绪测评系统 2 用途:用于群体性人群心理情绪早期筛查,以及个人心理障碍辅助诊断,同时传统心理量表诞生已经100多年历史,在人工智能及大数据推动下,必然推动心理健康行业的产业变革与…...

20道嵌入式经典面试题(附答案)
1.嵌入式系统中经常要用到无限循环,如何用C编写死循环 答:while(1){} 或者 for(;;) 2.程序的局部变量存在于哪里,全局变量存在于哪里,动态申请数据存在于哪里。 答:程序的局部变量存在于栈区;全局变量存在…...
python学习-代码调试器
目录 为什么学习调试器Pycharm Debugger示例所用代码布局调试工具栏 Debug Bar程序控制工具栏 pdb查看源代码 l list查看当前函数源代码 ll longlist打印变量 p查看调用栈w where向上移动当前帧 u up向上移动当前帧 d down运行当前行代码,在第一个可以停止的位置停下 s step继续…...

第十一章 综合推理
第十一章 综合推理 第一节 综合推理-排序 题-综合推理-分类1-排序 甲、乙、丙、丁四人的国籍分别为英国、俄国、法国、日本。乙比甲高,丙更矮;英国人比俄国人高,法国人最高;日本人比丁高。 这四个人的国籍是: A.甲…...

嵌入式开发之设置寄存器中指定位
0 Preface/Foreword 嵌入式开发,位操作是常用的运算,读写对应寄存器指定位从而设置不同的功能。 1 设置寄存器中的任意位 1.1 清零 举例,假设一个寄存器名字为FUNCCON,地址为0x00008000,该寄存器长度为4个byte。 #define FUNC…...
第十章 数学相关
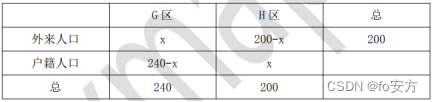
第十章 数学相关 第一节 集合 真题(2010-53)-数学相关-集合-画饼集能力-朴素逻辑 53.参加某国际学术研讨会的 60 名学者中,亚裔学者 31 人,博士 33 人,非亚裔学者中无博士学位的 4 人。根据上述陈述,参…...

数据结构——串(字符串)
文章目录 **一 串的定义和实现****1 定义****2 串的存储结构****2.1 定长顺序存储表示****2.2 堆分配存储表示****2.3 块链存储表示** **3 串的基本操作** **二 串的模式匹配****1 简单的模式匹配算法****2 串的模式匹配算法——KMP算法****2.1 字符串的前缀,后缀和…...
Seata服务端的启动过程 学习记录
1.ServerRunner ServerRunner类实现了CommandLineRunner与DisposableBean接口,将会在Spring容器启动和关闭的时间,分别执行 run 和 destory 方法。 而seata服务端的启动过程,都藏在run方法中 2.整体流程 io.seata.server.Server#start pu…...

Log4J
引言 为什么要用日志? --> 方便调试代码 什么时候用?什么时候不用? 出错调试代码时候用 生产环境下就不需要,就需要删除 怎么用? --> 输出语句 一、Log4J 1.1 介绍 log4j是Apache的一个开放源代码的项目,通过使用log4j,我们可以控…...

【零基础学机器学习 5】机器学习中的分类:什么是分类以及分类模型
👨💻 作者简介:程序员半夏 , 一名全栈程序员,擅长使用各种编程语言和框架,如JavaScript、React、Node.js、Java、Python、Django、MySQL等.专注于大前端与后端的硬核干货分享,同时是一个随缘更新的UP主. 你可以在各个…...

目标检测算法:Faster-RCNN论文解读
目标检测算法:Faster-RCNN论文解读 前言 其实网上已经有很多很好的解读各种论文的文章了,但是我决定自己也写一写,当然,我的主要目的就是帮助自己梳理、深入理解论文,因为写文章,你必须把你所写的东西表…...
基于Python的接口自动化-Requests模块
目录 引言 一、模块说明 二、Requests模块快速入门 1 发送简单的请求 2 发送带参数的请求 3 定制header头和cookie 4 响应内容 5 发送post请求 6 超时和代理 三、Requests实际应用 引言 在使用Python进行接口自动化测试时,实现接口请求…...

Vue框架中监测数组变化的方法
在 Vue 中,如果直接对数组进行操作,比如使用下标直接修改元素,数组长度不变时, Vue 是无法监测到这种变化的,导致无法触发视图更新。针对该问题,总结如下解决方法: 一、使用 Vue.js 提供的方法…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
