有关 string 类的练习(下)

目录
一、反转字符串 II
二、反转字符串中的单词 III
三、找出字符串中第一个只出现一次的字符
四、字符串相乘
五、把字符串转换成整数
一、反转字符串 II
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k个,则将剩余字符全部反转。 - 如果剩余字符小于
2k但大于或等于k个,则反转前k个字符,其余字符保持原样。
示例 1:
输入:s = "abcdefg", k = 2
输出:"bacdfeg"
示例 2:
输入:s = "abcd", k = 2
输出:"bacd"
提示:
1 <= s.length <= 10^4s仅由小写英文组成1 <= k <= 10^4
代码实现:
class Solution {
public:string reverseStr(string s, int k) {size_t pos = 0; // pos 为每次计数的起点while (pos < s.size()){if (pos + k <= s.size()) // 剩余字符大于等于 kreverse(s.begin() + pos, s.begin() + pos + k);else // 剩余字符小于 kreverse(s.begin() + pos, s.end());pos += 2 * k;}return s;}
};二、反转字符串中的单词 III
给定一个字符串 s ,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:
输入:s = "Let's take LeetCode contest"
输出:"s'teL ekat edoCteeL tsetnoc"
示例 2:
输入: s = "God Ding"
输出:"doG gniD"
提示:
1 <= s.length <= 5 * 10^4s包含可打印的 ASCII 字符。s不包含任何开头或结尾空格。s里 至少 有一个词。s中的所有单词都用一个空格隔开。
代码实现:
class Solution {
public:string reverseWords(string s) {size_t pos = 0; // pos 为每个待反转的单词的起点size_t found = s.find(' ', pos); // found 为每个待反转的单词的终点的下一个位置while (found != string::npos){reverse(s.begin() + pos, s.begin() + found);pos = found + 1;found = s.find(' ', pos);}reverse(s.begin() + pos, s.end()); // 反转最后一个单词return s;}
};三、找出字符串中第一个只出现一次的字符
描述:
找出字符串中第一个只出现一次的字符
数据范围:
输入的字符串长度满足 1≤ n ≤1000
输入描述:
输入一个非空字符串
输出描述:
输出第一个只出现一次的字符,如果不存在输出 -1
示例 1:
输入:asdfasdfo
输出:o
代码实现:
#include <iostream>
using namespace std;
int main()
{string s;cin >> s;// 统计 s 中的每个字符出现的次数int count[256] = { 0 };for (size_t i = 0; i < s.size(); ++i){count[s[i]] += 1;}
// 找出字符串中第一个只出现一次的字符bool flag = false; // 假设字符串中不存在只出现一次的字符for (size_t i = 0; i < s.size(); ++i){if (count[s[i]] == 1){flag = true;cout << s[i] << endl;break;}}if (flag == false)cout << -1 <<endl;return 0;
}四、字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1:
输入: num1 = "2", num2 = "3"
输出: "6"
示例 2:
输入: num1 = "123", num2 = "456"
输出: "56088"
提示:
1 <= num1.length, num2.length <= 200num1和num2只能由数字组成。num1和num2都不包含任何前导零,除了数字0本身。
代码实现:
class Solution {
public:// 字符串相加string add(string num1, string num2) {string ans;int end1 = num1.size() - 1, end2 = num2.size() - 1;size_t carry = 0; // 进位while (end1 >= 0 || end2 >= 0 || carry > 0){size_t val1 = end1 >= 0 ? (num1[end1--] - '0') : 0;size_t val2 = end2 >= 0 ? (num2[end2--] - '0') : 0;size_t sum = val1 + val2 + carry;
ans.insert(ans.begin(), sum % 10 + '0'); // 头插carry = sum / 10;}return ans;}
// 字符串相乘string multiply(string num1, string num2) {if (num1 == "0" || num2 == "0") // 特殊情况{return string("0");}// 思路:// 123 * 456 // = 123 * (400 + 50 + 6) // = [(123 * 4) * 100] + [(123 * 5) * 10] + (123 * 6)// 所以首先考虑计算出 123 * 6/5/4,然后在其后面添加适当的 '0',最后再将所有的积相加string ans;int end2 = num2.size() - 1;size_t count = 0; // 需要添加的 '0' 的数量while (end2 >= 0){size_t val2 = num2[end2--] - '0';string product;size_t carry = 0;int end1 = num1.size() - 1;while (end1 >= 0 || carry > 0){size_t val1 = end1 >= 0 ? (num1[end1--] - '0') : 0;size_t sum = val1 * val2 + carry;
product += sum % 10 + '0';carry = sum / 10;}reverse(product.begin(), product.end());product.append(count++, '0');ans = add(ans, product);}return ans;}
};五、把字符串转换成整数
描述:
将一个字符串转换成一个整数,要求不能使用字符串转换整数的库函数。 数值为 0 或者字符串不是一个合法的数值则返回 0
数据范围:
字符串长度满足 0≤ n ≤100
进阶:
空间复杂度 O(1) ,时间复杂度 O(n)
注意:
① 字符串中可能出现任意符号,出现除 +/- 以外符号时直接输出 0
② 字符串中可能出现 +/- 且仅可能出现在字符串首位。
输入描述:
输入一个字符串,包括数字字母符号,可以为空
返回值描述:
如果是合法的数值表达则返回该数字,否则返回0
示例 1:
输入:"+2147483647"
返回值:2147483647
示例 2:
输入:"1a33"
返回值:0
代码实现:
class Solution {
public:int StrToInt(string str) {// 如果是空字符串,则直接返回 0size_t sz = str.size();if (sz == 0)return 0;// 确定正负号size_t i = 0; int sign = 1; // 默认为正号if (str[0] == '+'){++i;}else if (str[0] == '-'){++i;sign = -1;}
// 确定绝对值int res = 0;while (i < sz){if (str[i] >= '0' && str[i] <= '9')res = res * 10 + (str[i] - '0');elsereturn 0;++i;}return sign * res;}
};相关文章:

有关 string 类的练习(下)
目录 一、反转字符串 II 二、反转字符串中的单词 III 三、找出字符串中第一个只出现一次的字符 四、字符串相乘 五、把字符串转换成整数 一、反转字符串 II 给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转…...

XuperChain搭建+报错+注意事项
安装依赖 golang 这里安装的是15-17版本 wget -c https://dl.google.com/go/go1.15.2.linux-amd64.tar.gz -O - | sudo tar -xz -C /usr/local 添加环境变量 这个可以通过添加下面的行到/etc/profile文件(系统范围内安装)或者$HOME/.profile文件(当前用户安装 vim /etc…...

【伏羲八卦图】(PythonMatlab实现)
目录 1 与达尔文对话 2 与老子对话 2.1 Python实现 2.2 Matlab实现 1 与达尔文对话 140年前,1858年7月1日,达尔文在英伦岛发表了自己有关自然选择的杰出论文。他提出,生物的发展规律是物竞天择。经过物竞,自然界选择并存留最具…...

ruoyi数据权限学习
思路 用户关联了角色(用户可以关联多个角色),给角色设置数据权限分类,数据权限分类有如下5种: 全部数据权限 - DATA_SCOPE_ALL自定数据权限 - DATA_SCOPE_CUSTOM部门数据权限 - DATA_SCOPE_DEPT部门及以下数据权限 -…...

WPF中实现动态导航
主页面 <mah:MetroWindowx:Class"Kx.View.MyMainView"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expression/bl…...

day16 | 104.二叉树的最大深度、111.二叉树的最小深度、 222.完全二叉树的节点个数
目录: 链接 题目链接: https://leetcode.cn/problems/maximum-depth-of-binary-tree/ https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/ https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/ 解题及思路学习 104…...

Spring Boot + Vue3前后端分离实战wiki知识库系统<八>--分类管理功能开发二
接着上一次Spring Boot Vue3 前后端分离 实战 wiki 知识库系统<七>--分类管理功能开发的分类功能继续完善。 分类编辑功能优化: 概述: 现在分类编辑时的界面长这样: 很明显目前的父分类的展现形式不太人性…...
类(一))
Python入门(十八)类(一)
类(一) 1.面向对象概述2.创建和使用类2.1 创建dog类2.2 根据类创建实例2.3 创建多个实例 1.面向对象概述 面向对象编程是最有效的软件编写方法之一。在面向对象编程中,你编写表示现实世界中的事物和情景的类,并基于这些类来创建对…...

c# 从零到精通-定义一个结构
c# 从零到精通-定义一个结构 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Test01 { class Program { public struct Rect//定义一个矩形结构 { public double width;//矩形的宽 public double height;//矩形的高 /// …...

检信ALLEMOTION非接触式心理情绪测评系统
1 名称:检信ALLEMOTION多维度心理情绪测评系统 2 用途:用于群体性人群心理情绪早期筛查,以及个人心理障碍辅助诊断,同时传统心理量表诞生已经100多年历史,在人工智能及大数据推动下,必然推动心理健康行业的产业变革与…...

20道嵌入式经典面试题(附答案)
1.嵌入式系统中经常要用到无限循环,如何用C编写死循环 答:while(1){} 或者 for(;;) 2.程序的局部变量存在于哪里,全局变量存在于哪里,动态申请数据存在于哪里。 答:程序的局部变量存在于栈区;全局变量存在…...
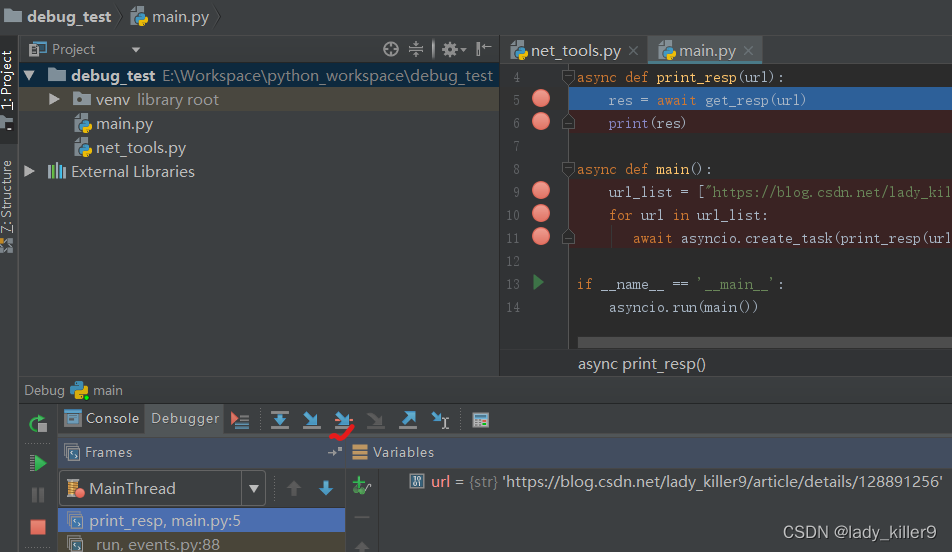
python学习-代码调试器
目录 为什么学习调试器Pycharm Debugger示例所用代码布局调试工具栏 Debug Bar程序控制工具栏 pdb查看源代码 l list查看当前函数源代码 ll longlist打印变量 p查看调用栈w where向上移动当前帧 u up向上移动当前帧 d down运行当前行代码,在第一个可以停止的位置停下 s step继续…...

第十一章 综合推理
第十一章 综合推理 第一节 综合推理-排序 题-综合推理-分类1-排序 甲、乙、丙、丁四人的国籍分别为英国、俄国、法国、日本。乙比甲高,丙更矮;英国人比俄国人高,法国人最高;日本人比丁高。 这四个人的国籍是: A.甲…...

嵌入式开发之设置寄存器中指定位
0 Preface/Foreword 嵌入式开发,位操作是常用的运算,读写对应寄存器指定位从而设置不同的功能。 1 设置寄存器中的任意位 1.1 清零 举例,假设一个寄存器名字为FUNCCON,地址为0x00008000,该寄存器长度为4个byte。 #define FUNC…...
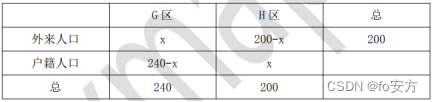
第十章 数学相关
第十章 数学相关 第一节 集合 真题(2010-53)-数学相关-集合-画饼集能力-朴素逻辑 53.参加某国际学术研讨会的 60 名学者中,亚裔学者 31 人,博士 33 人,非亚裔学者中无博士学位的 4 人。根据上述陈述,参…...

数据结构——串(字符串)
文章目录 **一 串的定义和实现****1 定义****2 串的存储结构****2.1 定长顺序存储表示****2.2 堆分配存储表示****2.3 块链存储表示** **3 串的基本操作** **二 串的模式匹配****1 简单的模式匹配算法****2 串的模式匹配算法——KMP算法****2.1 字符串的前缀,后缀和…...
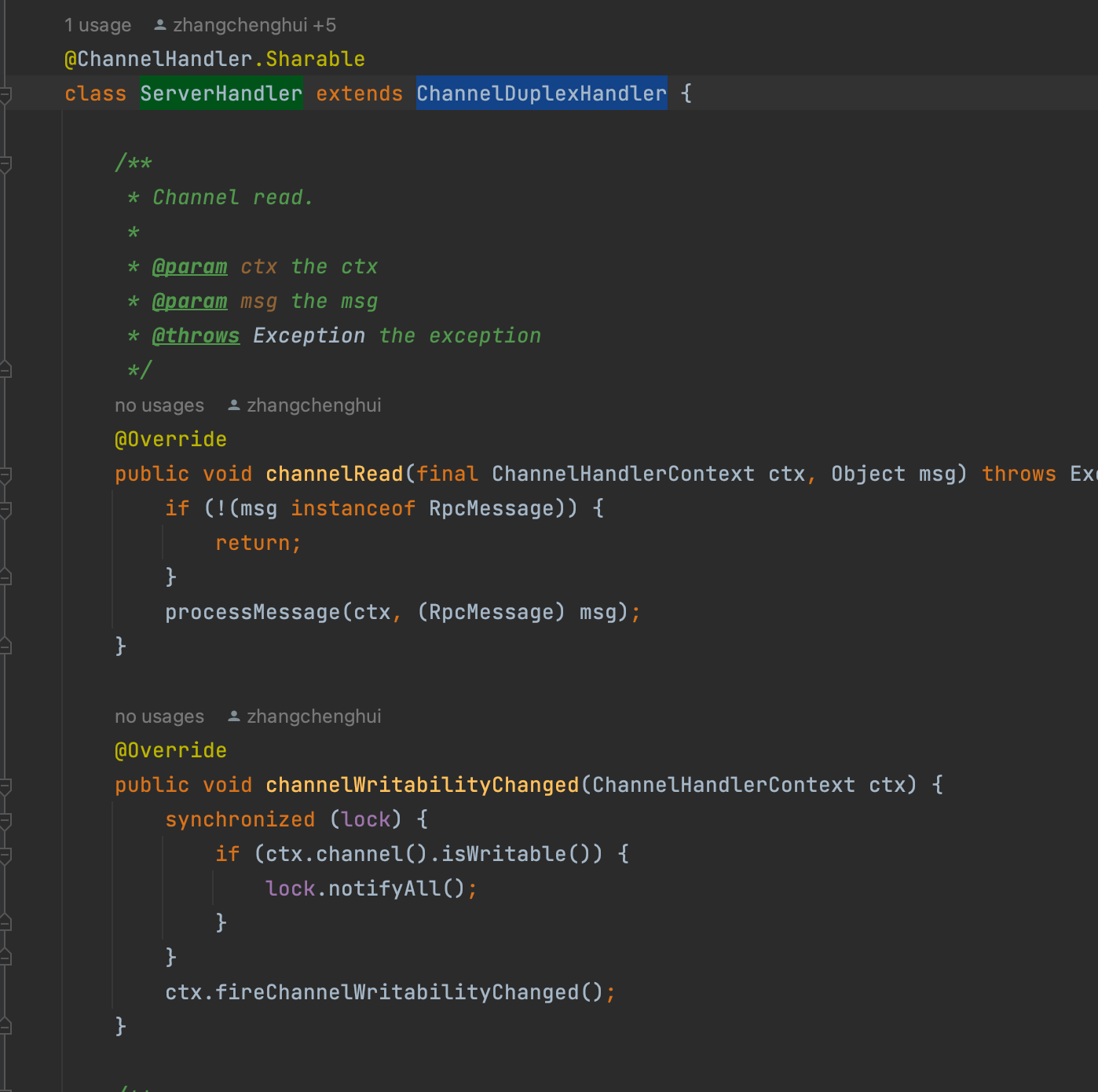
Seata服务端的启动过程 学习记录
1.ServerRunner ServerRunner类实现了CommandLineRunner与DisposableBean接口,将会在Spring容器启动和关闭的时间,分别执行 run 和 destory 方法。 而seata服务端的启动过程,都藏在run方法中 2.整体流程 io.seata.server.Server#start pu…...

Log4J
引言 为什么要用日志? --> 方便调试代码 什么时候用?什么时候不用? 出错调试代码时候用 生产环境下就不需要,就需要删除 怎么用? --> 输出语句 一、Log4J 1.1 介绍 log4j是Apache的一个开放源代码的项目,通过使用log4j,我们可以控…...

【零基础学机器学习 5】机器学习中的分类:什么是分类以及分类模型
👨💻 作者简介:程序员半夏 , 一名全栈程序员,擅长使用各种编程语言和框架,如JavaScript、React、Node.js、Java、Python、Django、MySQL等.专注于大前端与后端的硬核干货分享,同时是一个随缘更新的UP主. 你可以在各个…...

目标检测算法:Faster-RCNN论文解读
目标检测算法:Faster-RCNN论文解读 前言 其实网上已经有很多很好的解读各种论文的文章了,但是我决定自己也写一写,当然,我的主要目的就是帮助自己梳理、深入理解论文,因为写文章,你必须把你所写的东西表…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
