代码随想录刷题第48天|LeetCode198打家劫舍、LeetCode213打家劫舍II、LeetCode337打家劫舍III
1、LeetCode198打家劫舍
题目链接:198、打家劫舍
1、dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
2、递推公式:
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ;
如果不偷第i房间,那么dp[i] = dp[i - 1];
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])。
3、初始化:
递推公式的基础就是dp[0] 和 dp[1]。
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
4、遍历顺序: 从前向后遍历;
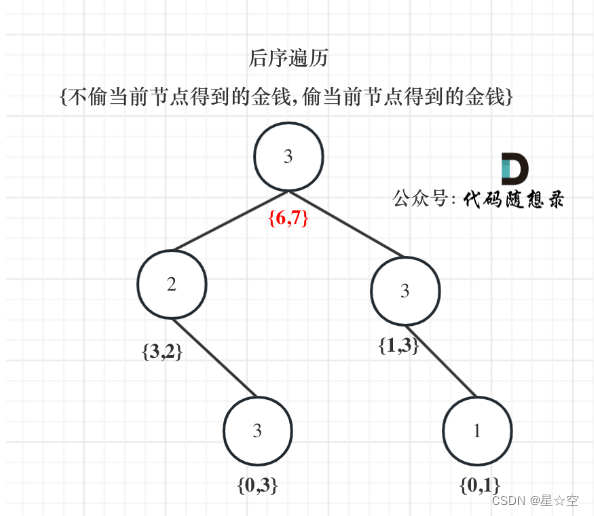
5、举例推导。
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size(), 0);dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++){dp[i] = max(dp[i-2] + nums[i], dp[i-1]);}return dp[nums.size() - 1];}
};2、LeetCode213打家劫舍II
题目链接:213、打家劫舍II
本题首尾连在一起,成环有三种情况:
考虑不包含首尾元素, 考虑包含首元素不包含尾元素, 考虑包含尾元素不包含首元素。
第二第三中情况包括第一种,所以只需考虑去掉首元素,去掉尾元素,这两种情况下,哪种的dp[i]更大。
递归五部曲与上题一样,由于要去掉首尾元素,定义一个start、end区间
robRange(vector<int>& nums, int start, int end)。
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robrange(nums, 0, nums.size()-2);int result2 = robrange(nums, 1, nums.size()-1);return max(result1, result2);}int robrange(vector<int>& nums, int start, int end){if (start == end) return nums[start];vector<int> dp(nums.size(), 0);dp[start] = nums[start];dp[start+1] = max(nums[start], nums[start+1]);for (int i = start + 2; i <= end; i++){dp[i] = max(dp[i-2] + nums[i], dp[i-1]);}return dp[end];}
};3、LeetCode337打家劫舍III
题目链接:337、打家劫舍III
第一次做树形dp,有点难理解。
1、dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
2、递归树时的终止条件:
如果遇到空节点的话,无论偷还是不偷都是0。
if (cur == NULL) return vector<int>{0,0}; 注意这里是花括号。
3、遍历顺序:
后序遍历。
递归左节点,得到左节点偷与不偷的金钱。
递归右节点,得到右节点偷与不偷的金钱。
4、递推公式:
偷该节点,则左右孩子不能偷,int val1 = cur->val + left[0] + left[1];
不偷该节点,则左右孩子要偷,每个孩子里偷一个最大的,int val2 = max(left[0],left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}。
5、举例推导:
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}vector<int> robTree(TreeNode* cur){if (cur == NULL) return vector<int>{0,0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);int val1 = cur->val + left[0] + right[0];int val2 = max(left[0], left[1]) + max(right[0], right[1]);return {val2,val1};}
};相关文章:

代码随想录刷题第48天|LeetCode198打家劫舍、LeetCode213打家劫舍II、LeetCode337打家劫舍III
1、LeetCode198打家劫舍 题目链接:198、打家劫舍 1、dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。 2、递推公式: 如果偷第i房间,那么dp[i] dp[i - 2] nums[i] …...

C# NTS 获取MuliiLineString中的所有线
/// <summary>/// 获取多段线的所有线/// </summary>/// <param name"ml"></param>/// <returns></returns>public static List<LineString> GetLineStrings(this MultiLineString ml){List<LineString> lineString…...
CodeWhisperer插件使用体验
官方教程点击跳转 使用工具 1.vscode 2.插件(AWS Toolkit),免费使用 安装以后如何使用 1.首先要有一个aws账号 2.插件下载好以后登录aws账号,我们主要用这款插件的CodeWhisperer这个功能,其它的自行看官方教程了解。 注意事项:我们在从vs…...
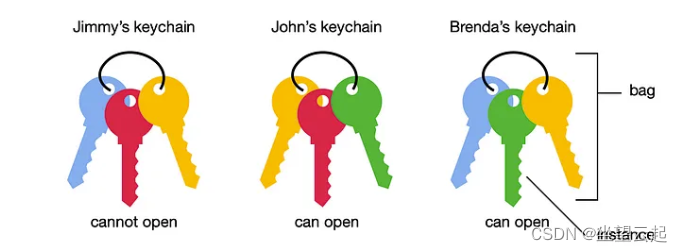
机器学习笔记 - 多实例学习(MIL)弱监督学习
一、多实例学习概述 多实例学习(MIL)是一种弱监督学习形式,其中训练实例被排列在称为袋的集合中,并为整个袋提供标签。这种方式越来越受到人们的关注,因为它自然适合各种问题,并允许利用弱标记数据。因此,它被应用于计算机视觉和文档分类等不同的应用领域。 多实例学习(…...
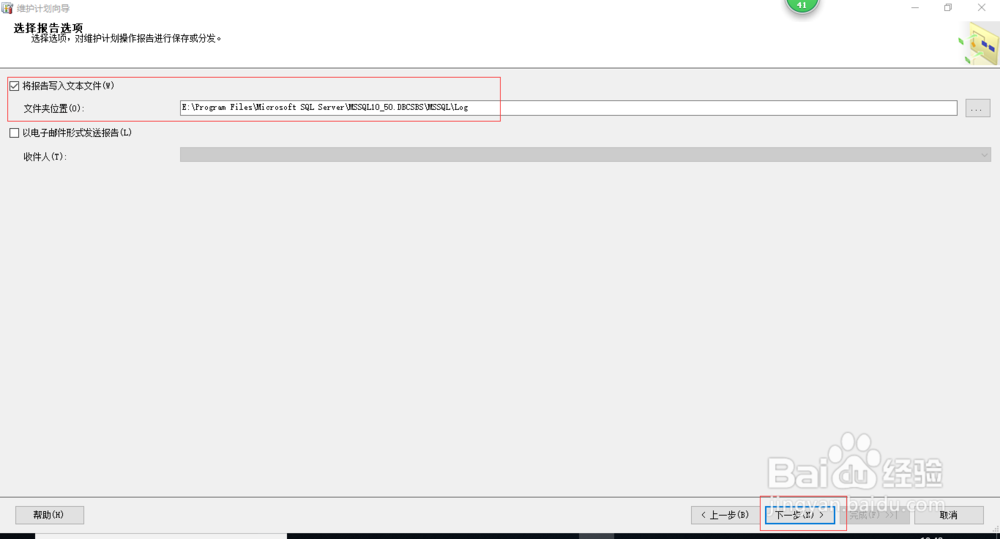
SQL Server 2008 定时自动备份和自动删除方法
SQL Server 2008 数据定时自动备份和自动删除方法,同一个计划兼备数据备份数数据删除的操作方法 工具/原料 SQL Server 2008 方法/步骤 1、 点击实例名下的【管理】-【维护计划】-点击鼠标右键,点击【维护计划向导】,填写计划名称&…...
代码生成器实现
代码生成器实现 实现封装元数据的工具类实现代码生成器的代码编写掌握模板创建的 构造数据模型 需求分析 借助Freemarker机制可以方便的根据模板生成文件,同时也是组成代码生成器的核心部分。对于Freemarker而 言,其强调 数据模型 模板 文件 的思…...
)
【Python基础】Python函数(基本函数)
文章目录 Python函数1、函数多返回值2、函数多种传参方式(1)位置参数(2)关键字参数(3)缺省参数(4)不定长参数位置传递关键字传递 3、小结 Python函数 1、函数多返回值 Q:如果一个函数要有多个返回值,该如何书写代码? # 使用多个变量&#…...

Vue3 + TS + Vite —— 大屏可视化 项目实战
前期回顾 Vue3 Ts Vite pnpm 项目中集成 —— eslint 、prettier、stylelint、husky、commitizen_彩色之外的博客-CSDN博客搭建VIte Ts Vue3项目并集成eslint 、prettier、stylelint、huskyhttps://blog.csdn.net/m0_57904695/article/details/129950163?spm1001.2014…...

EasyExcel 批量导入并校验数据
文章目录 前言一、pom二、使用步骤1.导入对象2.读入数据并保存 前言 EasyExcel 批量导入并校验数据 一、pom <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.7</version></depend…...

亚马逊、Allegro卖家建立属于自己的测评系统,实现批量优质账号养成
卖家搭建一套完整的测评系统,卖家自己能够养出批量优质账号,并完全掌控真实买家的浏览、加购、下单和评价等风控数据规律。我们的系统能够自主加速推广,防御反击,同时节省运营成本,实现高效的测评运营。 我们的系统支…...

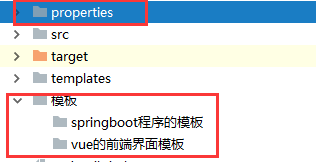
springboot的目录结构作用
springboot单体项目结构大概如下。 代码都在src/main下, java是后端代码 java下最基本的包 dao(mapper) entity(model) service controller 其他的包根据项目需求扩展。 resources下是配置文件。 如果不是前后端分离,resources下放的是静态文件…...

微信小程序基础使用-请求数据并渲染
小程序基本使用-请求数据并渲染 小程序模板语法-数据绑定 在js中定义数据 Page({data: {isOpen: true,message: hello world!} })小程序的data是一个对象,不同于vue的data是一个函数 在模块中获取使用数据 小程序中使用 {{}} 实现数据与模板的绑定 内容绑定&a…...

代码随想录训练营Day55| 392.判断子序列 ;115.不同的子序列
392.判断子序列 class Solution {public boolean isSubsequence(String s, String t) {int m s.length();int n t.length();if(m>n) return false;int[][] dp new int[m1][n1];dp[0][0]0;for(int i1;i<m;i){for(int j1;j<n;j){if(s.charAt(i-1)t.charAt(j-1)){dp[i…...

网络作业9【计算机网络】
网络作业9【计算机网络】 前言推荐网络作业9一. 单选题(共12题,36分)二. 多选题(共1题,3分)三. 填空题(共2题,10分)四. 阅读理解(共1题,17分&…...

C++ QT 上传图片至mysql数据库
以下是一个简单的C QT上传图片至MySQL数据库的代码示例: #include <QtSql> #include <QFile> #include <QByteArray> int main() { //连接数据库 QSqlDatabase db QSqlDatabase::addDatabase("QMYSQL"); …...
2023去水印小程序saas系统源码修复独立版v1.0.3+uniapp前端
🎈 限时活动领体验会员:可下载程序网创项目短视频素材 🎈 🎉 有需要的朋友记得关赞评,阅读文章底部来交流!!! 🎉 ✨ 源码介绍 一个基于uniapp写的小程序,后端…...

【ChatGPT】数据科学 ChatGPT Cheat Sheet 书籍分享(阿里云盘下载)
封皮 以下为书中部分内容的机器翻译 我们的重要提示指南 1. 以 AI 角色的描述开始提示。 例如,“你是{x}”或“我希望你扮演{x}”。如果您不确定,请尝试“你是一个有帮助的助手”。 例如,您是 OpenAI 的数据科学家,您正在研究大型…...

使用 Docker-compose 搭建lnmp
服务编排: 应用编排: 单机环境下:shell/python脚本多机/集群环境下:ansible、saltstack、pubbet docker容器编排: 单机:docker-compose多机/集群:docker swarm,mesos marathon&a…...

chatgpt赋能python:Python中的矩阵合并方法:介绍和使用方法
Python中的矩阵合并方法: 介绍和使用方法 矩阵合并是Python编程中常用的操作之一,特别是针对数据分析、机器学习和深度学习等领域。Python提供了多种方法来合并矩阵,本文将介绍这些方法并分享如何在实际应用中使用它们。 普通矩阵合并 最基础的矩阵合…...
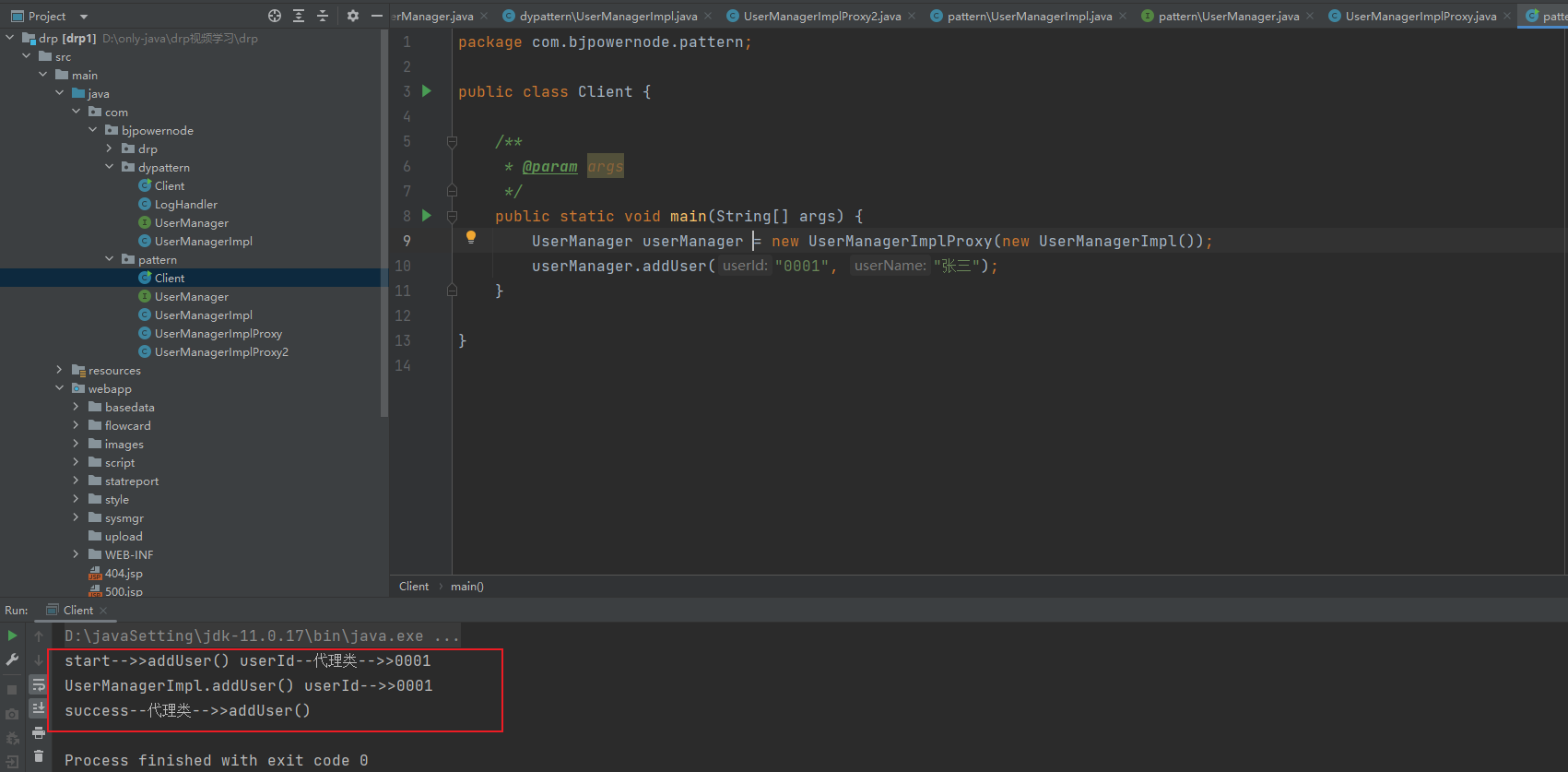
Java动态代理:优化静态代理模式的灵活解决方案
文章目录 代理模式定义具体实现分析优缺点 优化使用动态代理解决优化相关知识动态代理种类场景应用 代理模式 定义 代理模式,为其他对象提供一种代理以控制对这个对象的访问 具体实现 代理模式的具体实现描述可以分为以下几个步骤: 创建抽象对象接…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
