如何通过关键词搜索API接口
如果你是一位电商运营者或者是想要进行1688平台产品调研的人员,你可能需要借助API接口来获取你所需要的信息。在这篇文章中,我们将会讨论如何通过关键词搜索API接口获取1688的商品详情。
第一步:获取API接口的授权信息 在使用API接口前,你需要先向1688申请API接口的授权信息。在申请之前,你需要先获取key和密钥。
第二步:构建API接口调用请求 在获取授权之后,你需要根据相关接口文档,构建API接口调用请求。在这里,我们将以搜索商品接口为例,来讲解如何构建调用请求。
首先,你需要通过HTTP GET请求方式,来调用接口。相关调用信息如下:
请求参数:q=女装&start_price=0&end_price=0&page=1&cat=0&discount_only=&sort=&page_size=40&seller_info=no&nick=&seller_info=&nick=&ppath=&imgid=&filter=
参数说明:q:搜索关键字
cat:分类ID
start_price:开始价格
end_price:结束价格
sort:排序[bid,_bid,_sale,_credit]
(bid:总价,sale:销量,credit信用,加_前缀为从大到小排序)
page:页数 page_size:每页宝贝数量,默认40
filter:额外的过滤参数,如:filter=filtId:1,2,3,4;activityType:1,2,3,4;city:天津;quantityBegin:1000
filtId 过滤:48小时发货,7+天包换,赠运费险,免费赊账;
activityType 优惠类型:包邮,产地货源,伙拼,手机专享价
city 地区:地区名
quantityBegin 起订量:数字
相关文章:

如何通过关键词搜索API接口
如果你是一位电商运营者或者是想要进行1688平台产品调研的人员,你可能需要借助API接口来获取你所需要的信息。在这篇文章中,我们将会讨论如何通过关键词搜索API接口获取1688的商品详情。 第一步:获取API接口的授权信息 在使用API接口前&…...

智驾域控新战争打响,谁在抢跑?
智能驾驶域控制器赛道,已经成为了时下最为火热的市场焦点之一。 最近,头部Tier1均胜电子公布了全球首批基于高通Snapdragon Ride第二代芯片平台的智能驾驶域控制器产品nDriveH,在这一赛道中显得格外引人注意。 就在不久之前,均胜…...

Android 13无源码应用去掉无资源ID的按钮
Android Wifionly项目,客户要求去掉谷歌联系人里的 手机联系人按钮 需求分析 无应用源码,只能通过系统侧去修改 首先通过 Android Studio 工具 uiautomatorviewer 获取父控件资源ID chip_group ,然后通过遍历获取子控件去掉目标按钮 --- a/frameworks/base/core/java/andr…...
,正刊,SCIEEI双检,进化计算、模糊集和人工神经网络在数据不平衡中应用)
【SCI征稿】中科院2区(TOP),正刊,SCIEEI双检,进化计算、模糊集和人工神经网络在数据不平衡中应用
【期刊简介】IF:8.0-9.0,JCR1区,中科院2区(TOP) 【检索情况】SCIE&EI 双检,正刊 【数据库收录年份】2004年 【国人占比】22.78%(期刊国际化程度高) 【征稿领域】进化计算、模…...
)
Android Audio开发——AAudio基础(十五)
AAudio 是一个自 Android O 引入的新的 Android C API。它主要是为需要低延迟的高性能音频应用设计的。应用程序通过直接从流中读取或向流中写入数据来与 AAudio 通信,但它只包含基本的音频输入输出能力。 一、AAudio概述 AAudio 在应用程序和 Android 设备上的音频输入输出之…...
SDK接口远程调试【内网穿透】
文章目录 1.测试环境2.本地配置3. 内网穿透3.1 下载安装cpolar内网穿透3.2 创建隧道 4. 测试公网访问5. 配置固定二级子域名5.1 保留一个二级子域名5.2 配置二级子域名 6. 使用固定二级子域名进行访问 转发自cpolar内网穿透的文章:Java支付宝沙箱环境支付࿰…...

Mybatis学习笔记二
目录 一、MyBatis的各种查询功能1.1 查询一个实体类对象1.2 查询一个List集合1.3 查询单个数据1.4 查询一条数据为map集合1.5 查询多条数据为map集合1.5.1 方法一:1.5.2 方法二: 二、特殊SQL的执行2.1 模糊查询2.2 批量删除2.3 动态设置表名2.4 添加功能…...
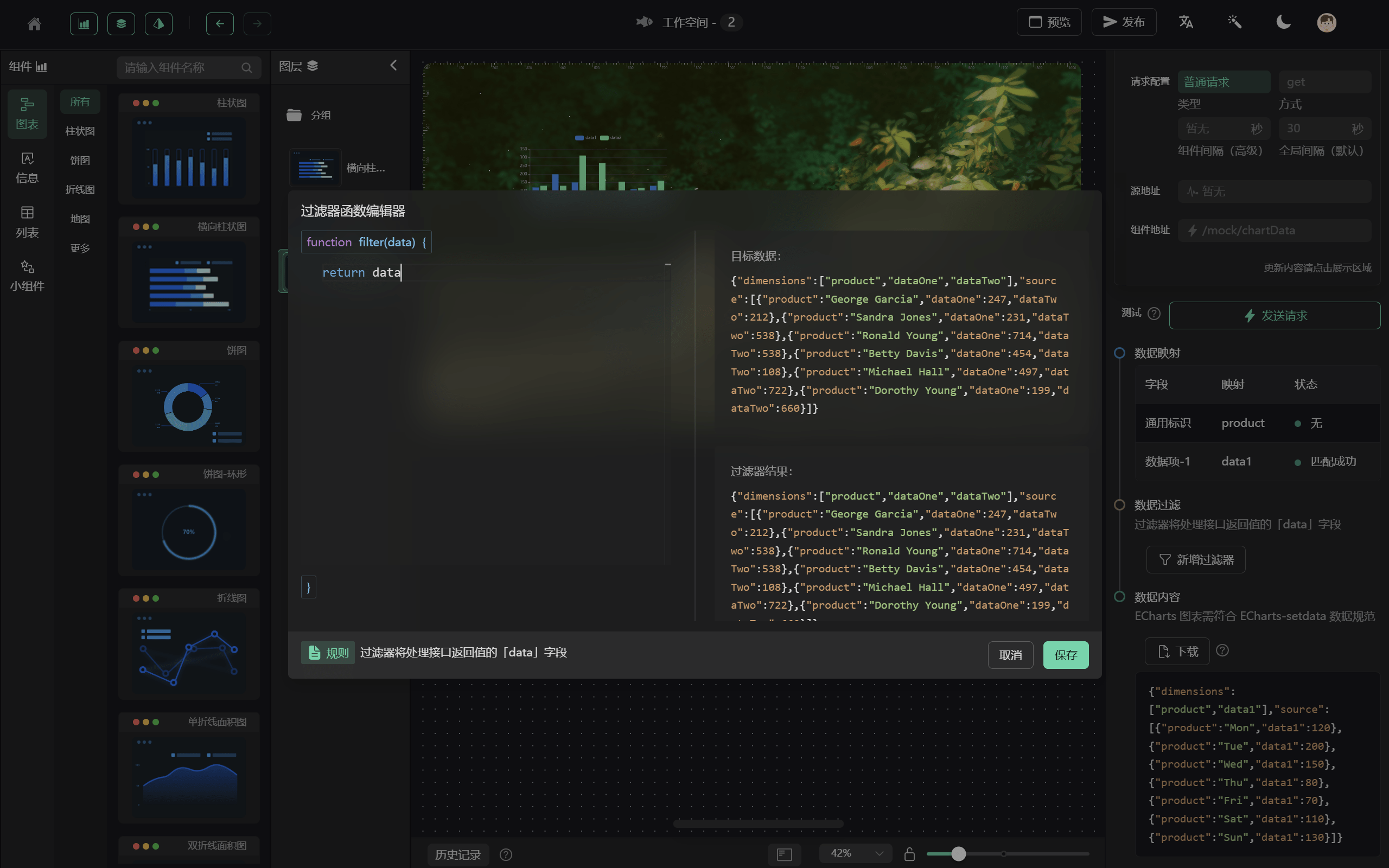
大屏数据可视化开源项目
一、DataGear —— 数据可视化项目 官网:DataGear - 开源免费的数据可视化分析平台 DataGear 是一款开源免费的数据可视化分析平台,数据可视化看板。 功能特性: 1、多种数据源,支持运行时接入任意提供 JDBC 驱动的数据库&#…...

面试经典150题:数组/字符串合集
新专栏,预计两个月写完吧,每天下班回来抽空做几道题。会把做题计划顺序记录下来,如果你有缘,刷到这个开篇序列,那就跟着文章去练题吧。初学者可以慢慢来 88. 合并两个有序数组 void merge(vector<int>& nums…...

Java源文件的执行过程
目录 1.JVM 2.字节码 3.Java源文件执行的过程 4.JIT(Just In Time Compilation) 5.AOT(Ahead Of Time Compilation) 6.AOT破坏Java动态性 7.编译型语言与解释型语言 8.Java-编译与解释并存的语言 9.Java和C的相同点与不同…...

10个ai算法常用库java版
今年ChatGPT 火了半年多,热度丝毫没有降下来。深度学习和 NLP 也重新回到了大家的视线中。有一些小伙伴问我,作为一名 Java 开发人员,如何入门人工智能,是时候拿出压箱底的私藏的学习AI的 Java 库来介绍给大家。 这些库和框架为机器学习、深度学习、自然语言处理等提供了广…...

怎么看服务器带宽大小 103.219.179.X
第一种,可以使用网站测速,这种方式比较便捷,但是由于网站测速是测试服务器发送数据包到他网站节点的一个速度情况,有时候节点问题或者服务器做了封包限制可能导致测试不准确的情况。 第二种,可以在IIS上架设一个大一点…...
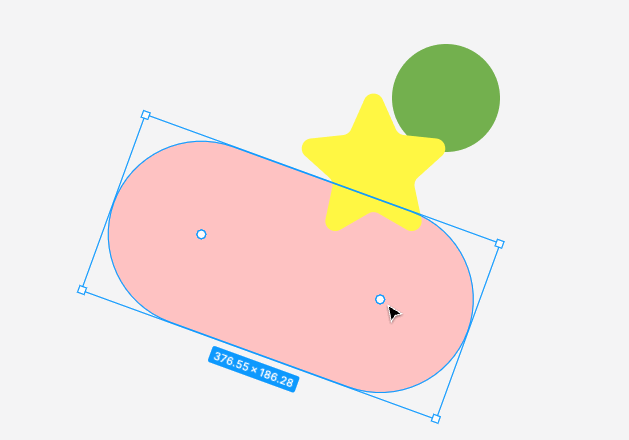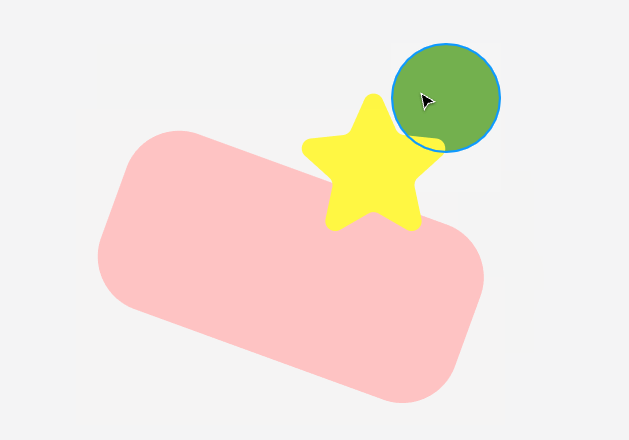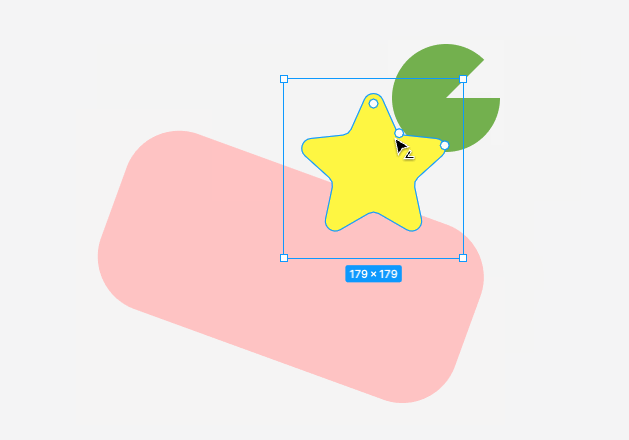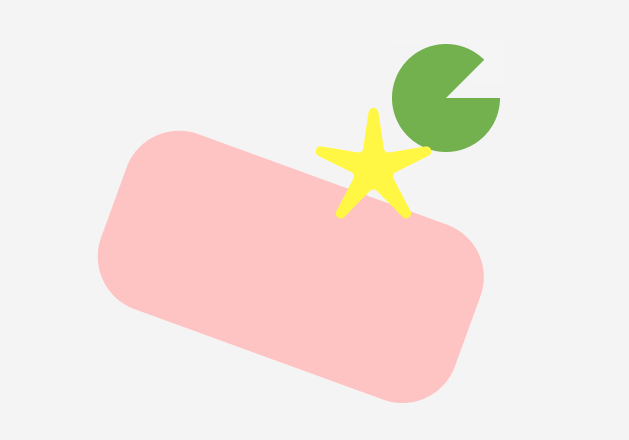
图形编辑器开发:最基础但却复杂的选择工具
大家好,我是前端西瓜哥。 对于一个图形设计软件,它最基础的工具是什么?选择工具。 但这个选择工具,却是相当的复杂。这次我来和各位,细说细说选择工具的一些弯弯道道。 我正在开发的图形设计工具的: http…...

apk签名-signapk.jar
如果做平台app开发,需要签platform签名,除了通过adroid.bp或者android.mk的方式使用AOSP整个大工程中签名外,还可以直接通过signapk.jar的方式进行签名,效率更高更快捷简便。 首先我们来回顾下AOSP平台签名的办法。 Android.mk 使…...
【100个高大尚求职简历】简历模板+修改教程+行业分类简历模板 (涵盖各种行业) (简历模板+编辑指导+修改教程)
文章目录 1 简历预览2 简历下载 很多人说自己明明投了很多公司的简历,但是都没有得到面试邀请的机会。自己工作履历挺好的,但是为什么投自己感兴趣公司的简历,都没有面试邀请的机会。反而是那些自己没有投递的公司,经常给自己打电…...

Nginx平滑升级版本或添加模块
文章目录 一、Nginx 平滑升级二、升级失败 回滚操作三、遇到问题 一、Nginx 平滑升级 一般有两种情况下需要升级 nginx,一种是确实要升级 nginx 的版本,另一种是要为 nginx 添加新的模块。 Nginx平滑升级其原理简单概括: (1&am…...
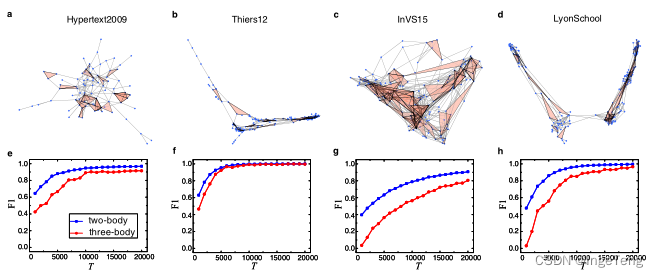
高阶复杂网络重建:从时间序列中重建高阶网络
论文链接:https://www.nature.com/articles/s41467-022-30706-9 一、为什么要研究高阶网络? 复杂网络跟我们生活息息相关,例如社交网络的信息传播,疾病的感染扩散和基因调控网络的相互作用等。越来越多的研究突破了传统网络中两…...
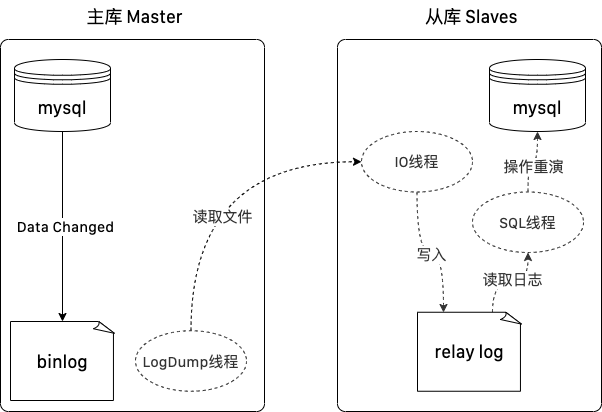
Day05 03-MySQL主从-主主原理与搭建详解
文章目录 第十六章 MySQL的系统架构(主从架构)16.1 MySQL集群架构的介绍16.1.1 主从架构介绍16.1.2 主从复制的原理 16.2 MySQL主从复制的实现16.2.1 环境说明16.2.2 主库配置16.2.3 从库配置16.2.4 主从复制测试 16.3 MySQL主主复制的实现16.3.1 主主复…...

STL之vector
目录 vector模拟实现一. vector的基本框架二. 常用方法及实现1.初始化和清理a. 默认构造函数b. 析构函数 2. 迭代器a. beginb. end 3.数据访问a. sizeb. capacityc. operator[]d. frontc. back 4.增删查改操作a. reserveb. resizec. insertd. push_backe. erasef. pop_back 5.构…...
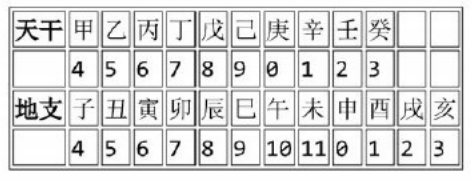
2020年CSP-J认证 CCF非专业级别软件能力认证第一轮真题-单项选择题解析
2020 CCF认证第一轮(CSP-J)真题 一、单项选择题 (共15题,每2分,共30分;每题有且有一个正确选项) 1、在内存储器中每个存储单元都被赋予一个唯一的序号,称为 A、下标 B、序号 C、地址 D、编号 答案:C…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
