力扣笔记(每日随机一题)——最佳买卖股票时机含冷冻期
问题(中等)
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/
示例 1
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2
输入: prices = [1]
输出: 0
提示:
1 < = p r i c e s . l e n g t h < = 5000 1 <= prices.length <= 5000 1<=prices.length<=5000
0 < = p r i c e s [ i ] < = 1000 0 <= prices[i] <= 1000 0<=prices[i]<=1000
解题
思路
(BP问题太折磨了,思路参考官方解答)
每一天可以有三个状态:买、卖和冷冻期;
temp[i]表示截至第i天,最后一个操作是卖时的最大收益;
buy[i]表示截至第i天,最后一个操作是买时的最大收益;
frozen[i]表示截至第i天,最后一个操作是冷冻期时的最大收益;
递推公式:
temp[i] = max(buy[i-1]+prices[i], temp[i-1]) (第一项表示第i天卖出,第二项表示第i天冷冻)
buy[i] = max(frozen[i-1]-prices[i], buy[i-1]) (第一项表示第i天买进,第二项表示第i天冷冻)
frozen[i] = max(temp[i-1], buy[i-1], frozen[i-1])
代码实现
class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)if n == 0:return 0 temp = [0]*nbuy = [0]*nfrozen = [0]*nbuy[0] = -prices[0]for i in range(1,n):temp[i] = max(buy[i-1] + prices[i], temp[i-1])buy[i] = max(frozen[i-1] - prices[i], buy[i-1])frozen[i] = max(temp[i-1], buy[i-1],frozen[i-1])return temp[-1]

相关文章:

力扣笔记(每日随机一题)——最佳买卖股票时机含冷冻期
问题(中等) 给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 卖出股票后&a…...
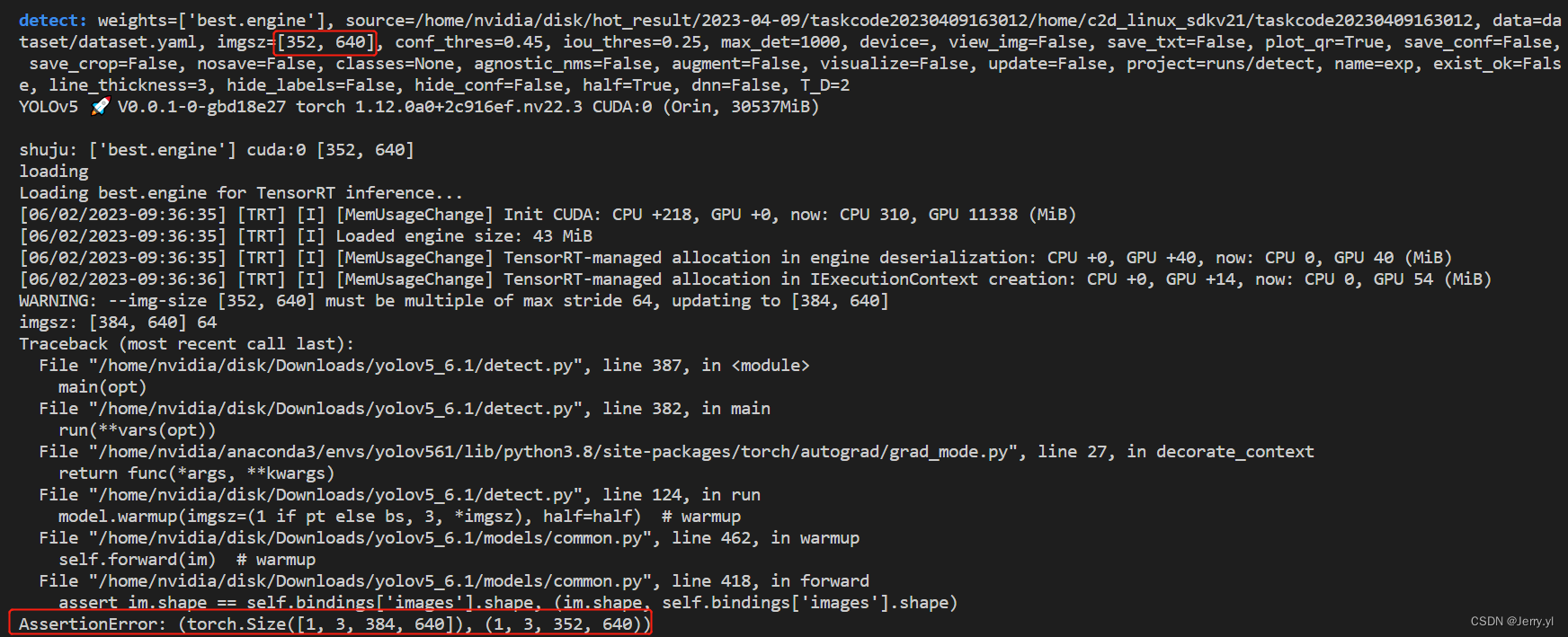
yolov5 6.1 关于 tensorrt 加速的使用以及问题说明
文章目录 1. 参考连接2. 使用说明2.1 导出加速模型2.1 使用加速模型2.2 加速参数对比 3. 问题说明3.1 在 Tensorrt 8.4.1.5 版本上使用 export.py 导出失败的问题3.2 把模型文件由 best.pt 更换成加速后的 best.engine 后,执行推理时标注的类别名不正确的问题3.3 导…...
用法介绍)
SVR(支持向量机)用法介绍
一、SVR回归介绍 SVR(Support Vector Regression)是支持向量机(SVM)在回归问题中的应用。与SVM分类模型相似,SVR也是一种非概率性算法,通过使用核函数将数据映射到高维空间,并在该空间上寻找最优的超平面与训练数据之间的间隔最大化…...

是面试官放水,还是公司实在是太缺人?这都没挂,腾讯原来这么容易进···
本人211非科班,之前在字节和腾讯实习过,这次其实没抱着什么特别大的希望投递,没想到腾讯可以再给我一次机会,还是挺开心的。 本来以为有个机会就不错啦!没想到能成功上岸,在这里要特别感谢帮我内推的同学&…...
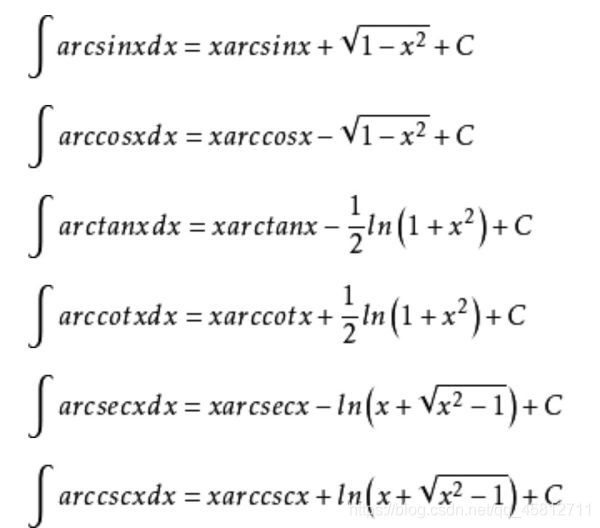
算法模板(5):数学(1):数学知识(1)
数论 整数的整除性 [x]表示不超过x的最大整数,叫做取整函数或高斯函数。设整数a,b不同时为零,则存在一对整数m,n,使得 ( a , b ) a m b n (a, b) am bn (a,b)ambn。注:a和b的最大公因数会写成 (a, b)…...
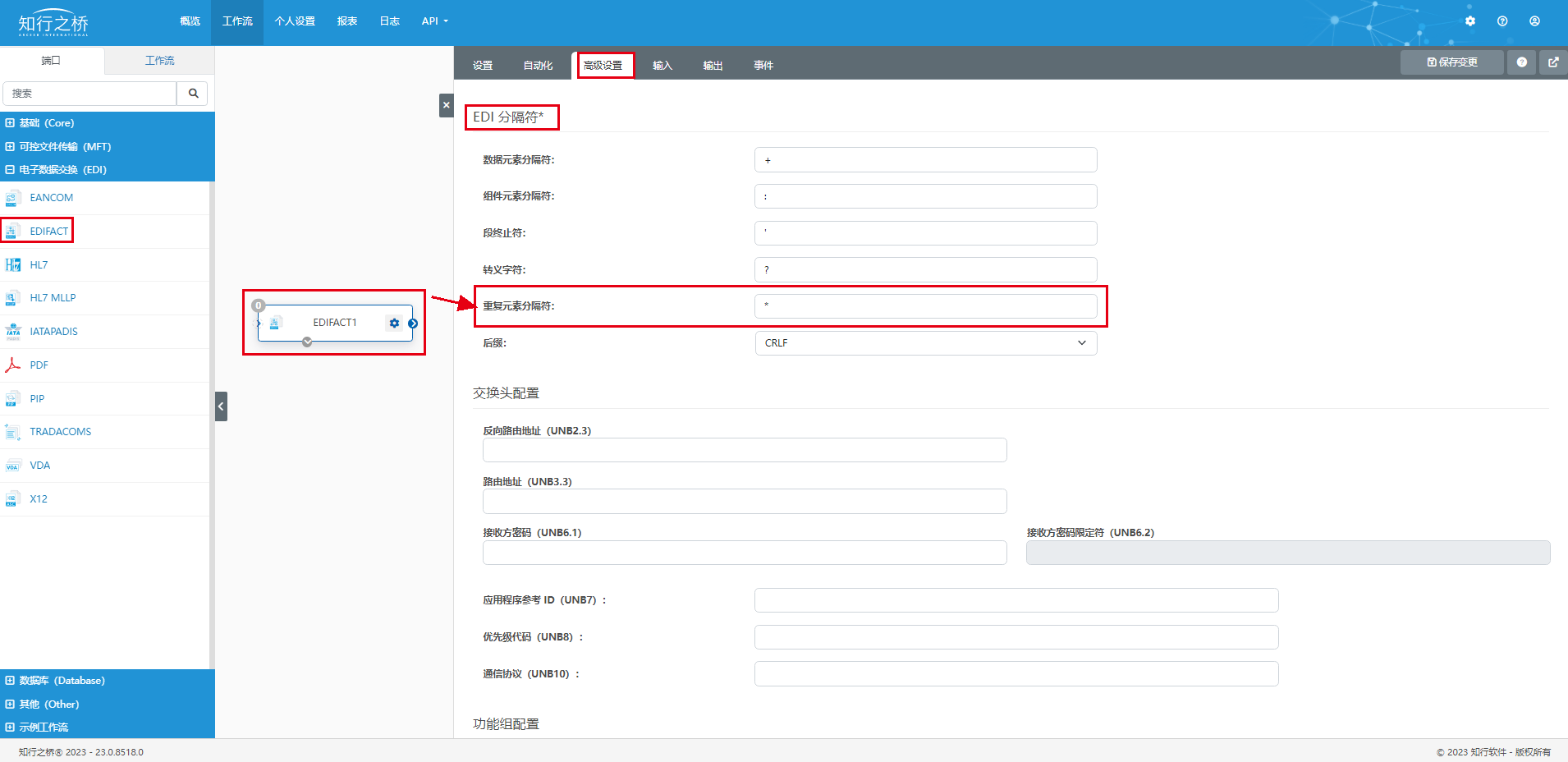
电子行业 K 公司对接 Nexperia EDI 项目案例
项目背景 Nexperia 是一家全球领先的半导体制造商,专注于提供高性能、高可靠性和创新性的半导体解决方案。公司成立于2017年,是前飞思卡尔半导体业务的一部分,并在全球范围内拥有多个设计、研发和生产基地。 Nexperia 使用 EDI(…...

chatgpt赋能python:Python如何将英文转化为中文的最佳方法
Python如何将英文转化为中文的最佳方法 介绍 在现代全球化社会中,国与国之间的交流越来越频繁,相应的语言翻译工具的需求也愈发迫切。Python是一种易于学习、快速上手的编程语言,适合初学者和经验丰富的程序员使用,在语言翻译方…...
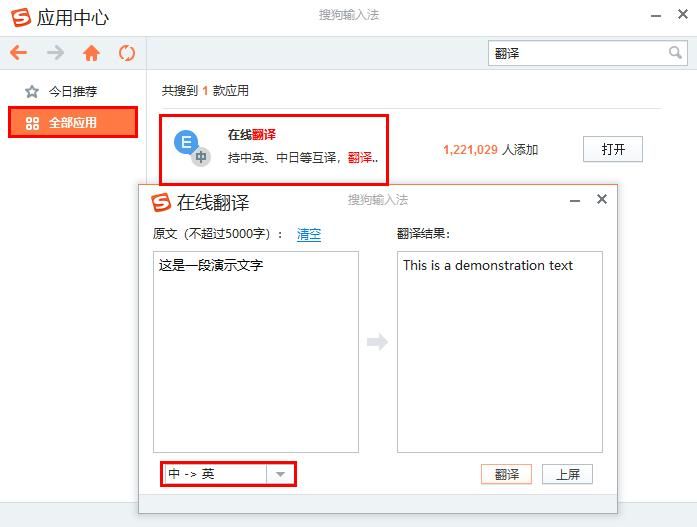
知道这些英文文档翻译的方式吗
在工作中,大家有没有遇到领导交给你一份外语的文档,要你去观看和理解,但是我们看不太懂或者没啥时间去一点点翻译怎么办呢?我们就需要有工具来将文档翻译,它是一项非常实用和便捷的功能,它可以将文档中的文…...
供应链安全
供应链安全 目录 文章目录 供应链安全目录本节实战可信任软件供应链概述构建镜像Dockerfile文件优化镜像漏洞扫描工具:Trivy检查YAML文件安全配置:kubesec准入控制器: Admission Webhook准入控制器: ImagePolicyWebhook关于我最后…...

华硕天选4原装Windows11系统带ASUSRECOVERY恢复工厂模式安装
华硕工厂恢复系统 ,安装结束后带隐藏分区以及机器所有驱动软件,奥创Myasus Recovery 文件地址https://pan.baidu.com/s/1Pq09oDzmFI6hXVdf8Vqjqw?pwd3fs8 提取码:3fs8 文件格式:5个底包(HDI KIT COM MCAFEE EDN) 1个引导工具TLK 支持ASUSRECOVERY型…...
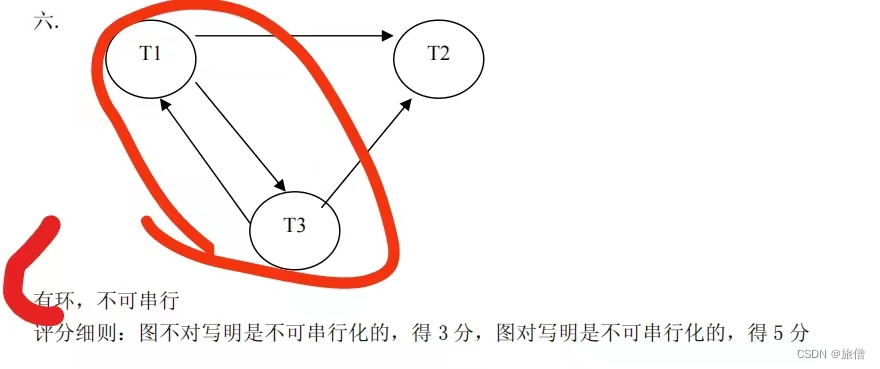
数据库期末复习(8)并发控制
笔记 数据库DBMS并发控制(1)_旅僧的博客-CSDN博客 数据库 并发控制(2)死锁和意向锁_旅僧的博客-CSDN博客 同一个对象不能既有slock又有xlock; 冲突可串行化和锁 怎么判断是否可以进行冲突可串行化:简便的方法是优先图 只有不同对象和同一对象都是读才不能发生非串行化调…...
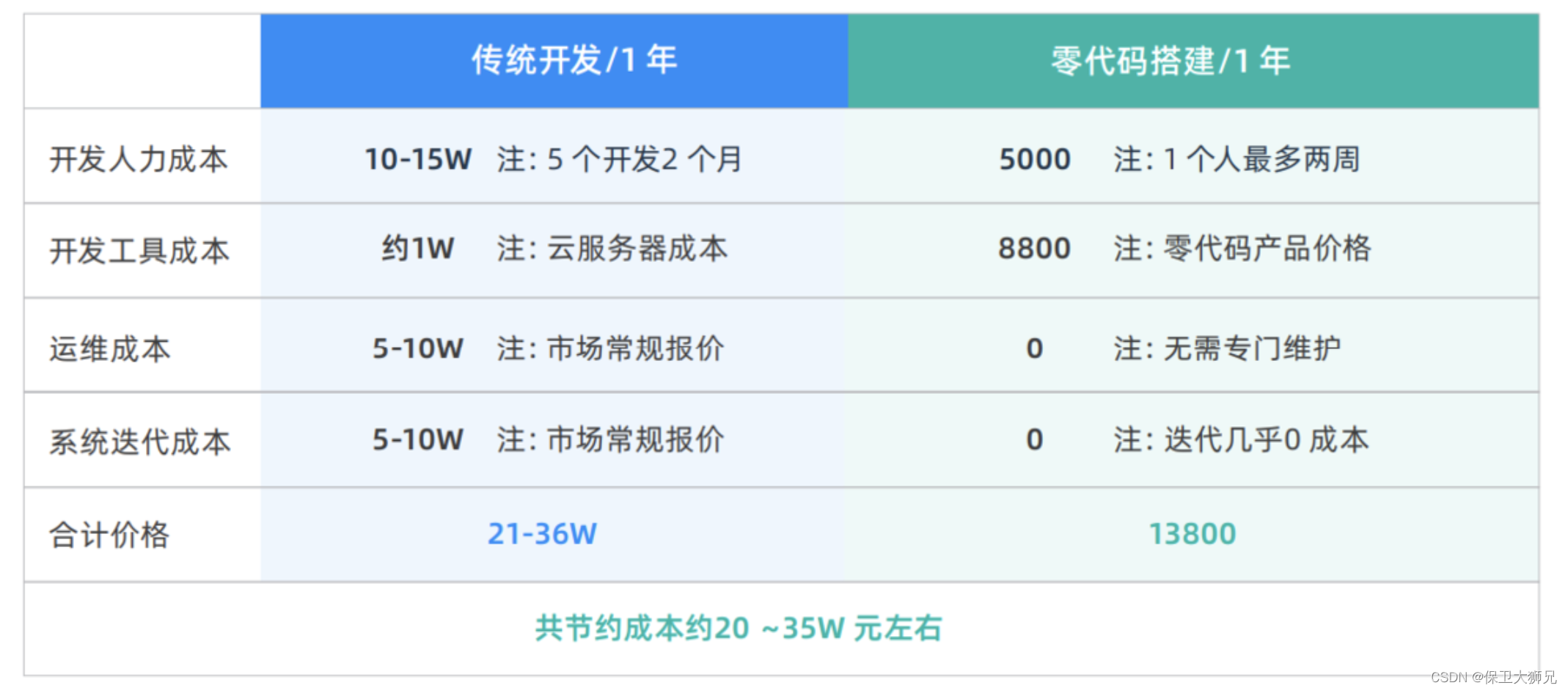
一文说透:低代码开发平台和零代码平台区别是什么?
低代码开发平台和零代码平台区别是什么? 一个简单的例子就可以解释清楚。 假设你想入住一套新房,回看住房变迁史: 最原始方式是:自己建造往后一点,交付“毛坯房”:开发商统一建小区,不需要自…...

4.将图神经网络应用于大规模图数据(Cluster-GCN)
到目前为止,我们已经为节点分类任务单独以全批方式训练了图神经网络。特别是,这意味着每个节点的隐藏表示都是并行计算的,并且可以在下一层中重复使用。 然而,一旦我们想在更大的图上操作,由于内存消耗爆炸,…...

pymongo更新数据
使用 PyMongo,可以通过以下步骤将查询到的记录进行更新: 下面是一个简单的示例代码片段,展示如何向名为users的集合中的所有文档添加一个新字段age。 import pymongo # 连接 MongoDB client pymongo.MongoClient("mongodb://localh…...
)
手机软件测试规范(含具体用例)
菜单基本功能测试规范一、短消息功能测试规范测试选项操作方法观察与判断结果创建、编辑短消息并发送书写短消息1、分别使用菜单或快捷方式进入书写短消息是否有异常; 2、输入0个字符,选择、输入号码发送,应成功; 3、输入1个中文…...

mysql having的用法
having的用法 having字句可以让我们筛选成组后的各种数据,where字句在聚合前先筛选记录,也就是说作用在group by和having字句前。而 having子句在聚合后对组记录进行筛选。我的理解就是真实表中没有此数据,这些数据是通过一些函数生存。 SQ…...
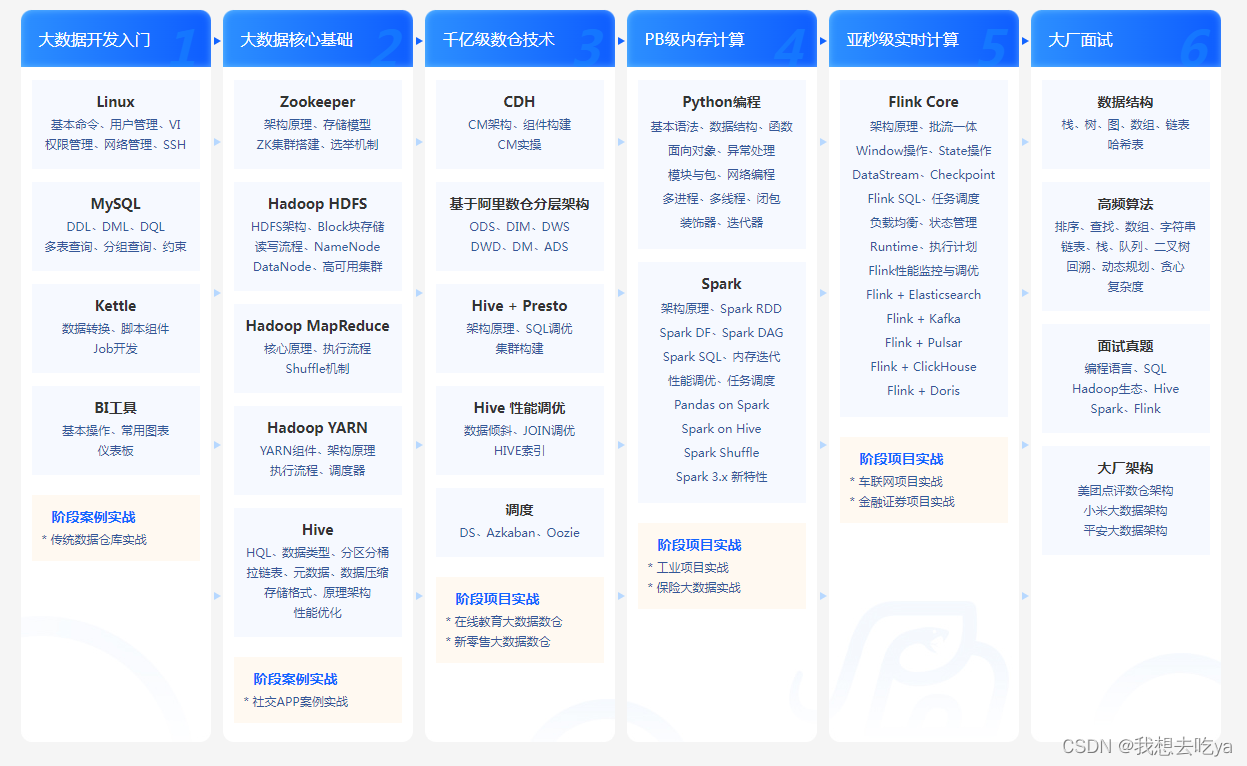
大数据需要学习哪些内容?
大数据技术的体系庞大且复杂,每年都会涌现出大量新的技术,目前大数据行业所涉及到的核心技术主要就是:数据采集、数据存储、数据清洗、数据查询分析和数据可视化。 Python 已成利器 在大数据领域中大放异彩 Python,成为职场人追求…...
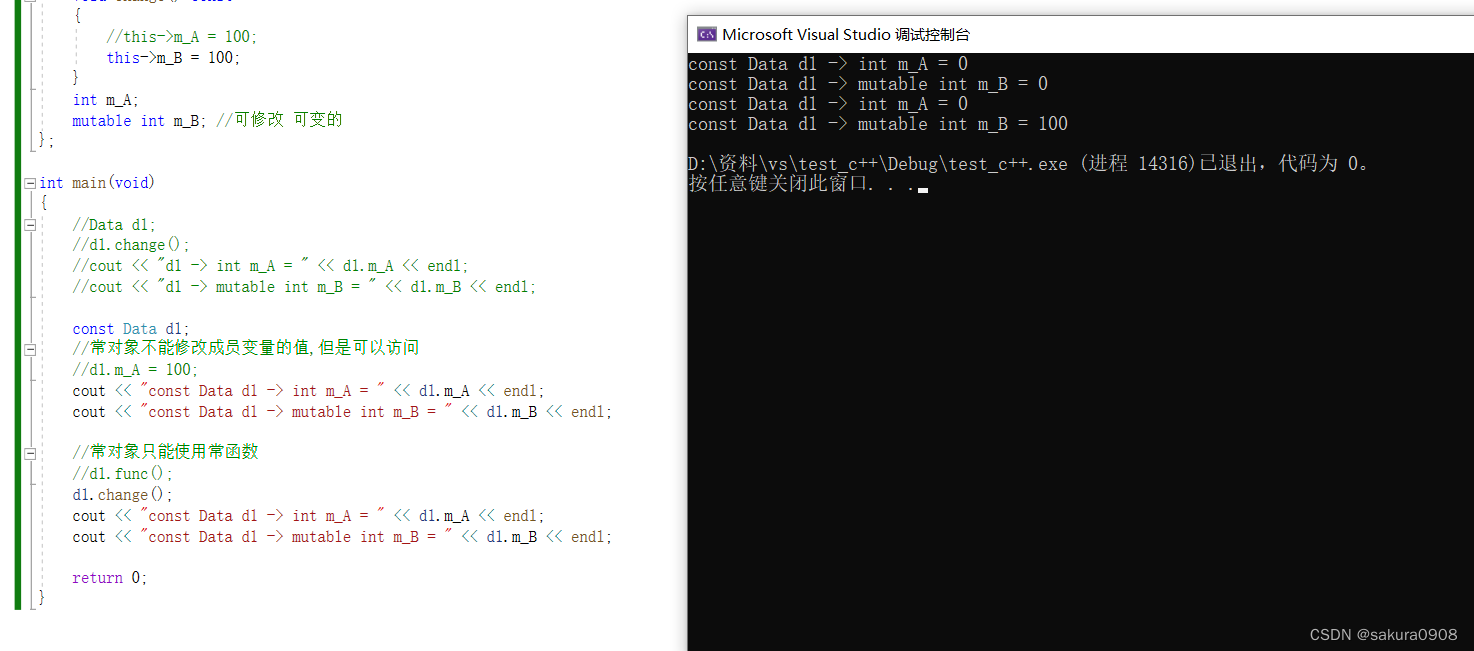
【c++】static和const修饰类的成员变量或成员函数
目录 1、静态成员变量 2、静态成员函数 3、常函数 4、常对象 当我们使用c的关键字static修饰类中的成员变量和成员函数的时候,此时的成员变量和成员函数被称为静态成员。 静态成员包含: 静态成员变量静态成员函数 1、静态成员变量 静态成员变量有…...
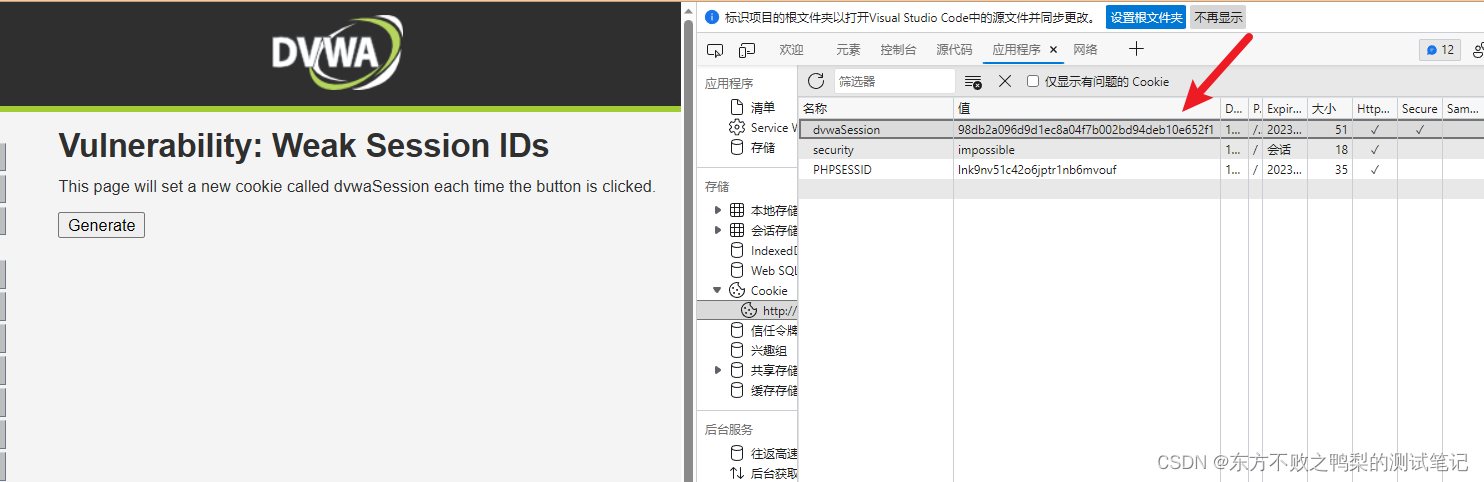
DVWA-9.Weak Session IDs
大约 了解会话 ID 通常是在登录后以特定用户身份访问站点所需的唯一内容,如果能够计算或轻松猜测该会话 ID,则攻击者将有一种简单的方法来访问用户帐户,而无需暴力破解密码或查找其他漏洞,例如跨站点脚本。 目的 该模块使用四种…...
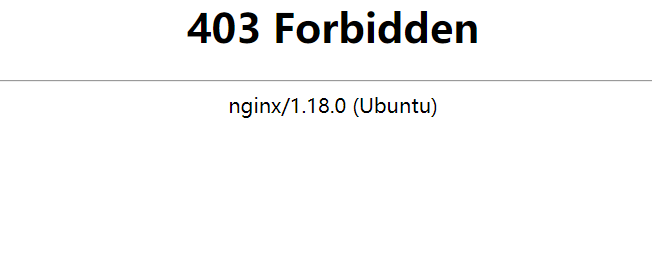
Bug序列——容器内给/root目录777权限后无法使用ssh免密登录
Linux——创建容器并将本地调试完全的前后端分离项目打包上传docker运行_北岭山脚鼠鼠的博客-CSDN博客 接着上一篇文章结尾出现403错误时通过赋予/root目录以777权限解决403错误。 chmod 777 /root 现在又出现新的问题,远程ssh无法免密登录了,即使通过…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
