逆函数学习
逆函数
给定关系 R ⊆ X × Y R\subseteq X\times Y R⊆X×Y,颠倒 R R R的所有有序偶可以得到 R R R的逆关系 R ~ ⊆ Y × X \tilde{R}\subseteq Y\times X R~⊆Y×X
但是对于函数 f : X → Y f:X\to Y f:X→Y而言,其逆关系 f ~ \tilde{f} f~可能不是 Y Y Y到 X X X的函数,
那么在什么条件下 f f f的逆关系 f ~ \tilde{f} f~能够称为函数呢?
定理1:设 f : X → Y f:X\to Y f:X→Y是双射,则 f f f的逆关系 f ~ \tilde{f} f~是从 Y Y Y到 X X X的函数
证明:设函数 f = { < x , y > ∣ x ∈ X ∧ y ∈ Y ∧ f ( x ) = y } f=\left\{\left<x,y\right> | x\in X \wedge y \in Y \wedge f\left(x\right)=y \right\} f={⟨x,y⟩∣x∈X∧y∈Y∧f(x)=y},则
f ~ = { < y , x > ∣ < x , y > ∈ f } \tilde{f}=\left\{\left<y,x\right>|\left<x,y\right>\in f\right\} f~={⟨y,x⟩∣⟨x,y⟩∈f}
对于任意的 y ∈ Y y\in Y y∈Y,由于 f f f是满射,所以有 x ∈ X x\in X x∈X,使得 < x , y > ∈ f \left<x,y\right>\in f ⟨x,y⟩∈f,即有 < y , x > ∈ f ~ \left<y,x\right>\in \tilde{f} ⟨y,x⟩∈f~,亦即 d o m ( f ~ ) = Y \mathop{dom}\left(\tilde{f}\right)=Y dom(f~)=Y
对于任意的 y ∈ Y y\in Y y∈Y,若有 x 1 , x 2 , ∈ X x_1,x_2,\in X x1,x2,∈X,使得 < y , x 1 > ∈ f ~ , < y , x 2 > ∈ f ~ \left<y,x_1\right>\in \tilde{f}, \left<y,x_2\right>\in\tilde{f} ⟨y,x1⟩∈f~,⟨y,x2⟩∈f~,则
< x 1 , y > ∈ f , < x 2 , y > ∈ f \left<x_1, y\right>\in f,\left<x_2,y\right>\in f ⟨x1,y⟩∈f,⟨x2,y⟩∈f,由于 f f f单射,所以 x 1 = x 2 x_1=x_2 x1=x2
由此可见,对于任意的 y ∈ Y y\in Y y∈Y,存在唯一的 x ∈ X x\in X x∈X,使得 < y , x > ∈ f ~ \left<y,x\right>\in \tilde{f} ⟨y,x⟩∈f~,故 f ~ \tilde{f} f~是函数
由于双射函数 f : X → Y f:X\to Y f:X→Y的逆关系也是函数,我们称这个哈数为 f f f的逆函数
记为 f − 1 : Y → X f^{-1}:Y\to X f−1:Y→X
定理2:设 f f f是从 X X X到 Y Y Y的双射, g g g是从 Y Y Y到 X X X的函数,则
f − 1 = g f^{-1}=g f−1=g当且仅当 g ∘ f = 1 X g\circ f=1_X g∘f=1X且 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y
证明:
必要性:若 f − 1 = g f^{-1}=g f−1=g,则对任意的 x ∈ X x\in X x∈X,由 < x , f ( x ) > ∈ f \left<x,f\left(x\right)\right>\in f ⟨x,f(x)⟩∈f可得 < f ( x ) , x > ∈ f − 1 \left<f\left(x\right),x\right>\in f^{-1} ⟨f(x),x⟩∈f−1
即 < f ( x ) , x > ∈ g \left<f\left(x\right),x\right>\in g ⟨f(x),x⟩∈g,所以 g ( f ( x ) ) = x g\left(f\left(x\right)\right) = x g(f(x))=x,即 g ∘ f ( x ) = 1 X ( x ) g \circ f\left(x\right) = 1_X\left(x\right) g∘f(x)=1X(x)
因此 g ∘ f = 1 X g\circ f=1_X g∘f=1X,同理可证 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y
充分性:先证 f − 1 ⊆ g f^{-1}\subseteq g f−1⊆g
对于任意的 < y , x > ∈ f − 1 \left<y,x\right>\in f^{-1} ⟨y,x⟩∈f−1,有 < x , y > ∈ f \left<x,y\right> \in f ⟨x,y⟩∈f,即 y = f ( x ) y=f\left(x\right) y=f(x),因为 g ∘ f = 1 X g\circ f=1_X g∘f=1X,所以有
g ( y ) = g ( f ( x ) ) = g ∘ f ( x ) = 1 X ( x ) = x g\left(y\right)=g\left(f\left(x\right)\right)=g\circ f\left(x\right)=1_X\left(x\right)=x g(y)=g(f(x))=g∘f(x)=1X(x)=x
因此 < y , x > ∈ g \left<y,x\right> \in g ⟨y,x⟩∈g,从而 f − 1 ⊆ g f^{-1}\subseteq g f−1⊆g
再证 g ⊆ f − 1 g\subseteq f^{-1} g⊆f−1,对任意的 < y , x > ∈ g \left<y,x\right>\in g ⟨y,x⟩∈g,即 x = g ( y ) x=g\left(y\right) x=g(y),因 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y,所以有
f ( x ) = f ( g ( y ) ) = f ∘ g ( y ) = 1 Y ( y ) = y f\left(x\right)=f\left(g\left(y\right)\right) = f\circ g\left(y\right)=1_Y\left(y\right) = y f(x)=f(g(y))=f∘g(y)=1Y(y)=y
因此 < x , y > ∈ f \left<x,y\right>\in f ⟨x,y⟩∈f,即有 < y , x > ∈ f − 1 \left<y,x\right>\in f^{-1} ⟨y,x⟩∈f−1,从而 g ⊆ f − 1 g\subseteq f^{-1} g⊆f−1
由 f − 1 ⊆ g f^{-1} \subseteq g f−1⊆g和 g ⊆ f − 1 g\subseteq f^{-1} g⊆f−1,于是 f − 1 = g f^{-1}=g f−1=g
由这个定理,可以等价地给出逆函数的另一定义
定义:设 f : X → Y f:X\to Y f:X→Y,若有 g : Y → X g:Y\to X g:Y→X使得 g ∘ f = 1 X g\circ f=1_X g∘f=1X和 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y成立,则称 g g g是 f f f的逆函数,并称 f f f是可逆的
定义:设 f : X → Y f:X\to Y f:X→Y
(1)若有 g : Y → X g:Y\to X g:Y→X,使得 g ∘ f = 1 X g\circ f=1_X g∘f=1X成立,则称 g g g是 f f f的左逆函数,并称 f f f是左可逆的
(2)若有 g : Y → X g:Y\to X g:Y→X,使得 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y成立,则称 g g g是 f f f的右逆函数,并称 f f f是右可逆的
定理3:设 f : X → Y , X ≠ ∅ f:X\to Y, X\neq \empty f:X→Y,X=∅,则
(1) f f f是左可逆的当且仅当 f f f是单射
(2) f f f是右可逆的当且仅当 f f f是满射
(3) f f f是可逆的当且仅当 f f f是双射,或当且仅当 f f f既是左可逆的,又是右可逆的
证明:
(1)必要性:若 f f f是左可逆的,则有 g : Y → X g:Y\to X g:Y→X,使得 g ∘ f = 1 X g\circ f=1_X g∘f=1X
对任意的 x 1 , x 2 ∈ x x_1,x_2\in x x1,x2∈x,若 f ( x 1 ) = f ( x 2 ) f\left(x_1\right)=f\left(x_2\right) f(x1)=f(x2),则
x 1 = 1 X ( x 1 ) = g ∘ f ( x 1 ) = g ( f ( x 1 ) ) = g ( f ( x 2 ) ) = g ∘ f ( x 2 ) = 1 X ( x 2 ) = x 2 \begin{aligned} x_1 &=1_X\left(x_1\right) = g\circ f\left(x_1\right) = g\left(f\left(x_1\right)\right)=g\left(f\left(x_2\right)\right)\\ &=g\circ f\left(x_2\right)=1_X\left(x_2\right)=x_2 \end{aligned} x1=1X(x1)=g∘f(x1)=g(f(x1))=g(f(x2))=g∘f(x2)=1X(x2)=x2
充分性:若 f f f是单射,则因 X ≠ ∅ X\neq \empty X=∅,任取 x 0 ∈ X x_0 \in X x0∈X,构造 g g g如下:
g : Y → X g ( y ) = { x , ∃ x ∈ X , y = f ( x ) x 0 , o t h e r w i s e g:Y\to X\\ g\left(y\right) = \begin{cases} x, &\exists x\in X, y=f\left(x\right)\\ x_0,&otherwise \end{cases} g:Y→Xg(y)={x,x0,∃x∈X,y=f(x)otherwise
则 g g g是函数,这是因为任意的 y ∈ Y y\in Y y∈Y
1.若 y ∈ f ( X ) y\in f\left(X\right) y∈f(X),则由于 f f f是单射,所以存在唯一的 x ∈ X x\in X x∈X,使得 < y , x > ∈ g \left<y,x\right>\in g ⟨y,x⟩∈g
2.若 y ∉ f ( X ) y\notin f\left(X\right) y∈/f(X),则有唯一的 x 0 ∈ X x_0\in X x0∈X,使得 < y , x 0 > ∈ g \left<y,x_0\right>\in g ⟨y,x0⟩∈g
并且对于任意的 x ∈ X x\in X x∈X
g ∘ f ( x ) = g ( f ( x ) ) = x = 1 X ( x ) g\circ f\left(x\right) = g\left(f\left(x\right)\right) = x = 1_X\left(x\right) g∘f(x)=g(f(x))=x=1X(x)
即 g ∘ f = 1 X g\circ f=1_X g∘f=1X,故 f f f是左可逆的
(2)
必要性:若 f f f是右可逆的,则有 g : Y → X g:Y\to X g:Y→X使得 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y,对于任意的 y ∈ Y y\in Y y∈Y,则有 g ( y ) ∈ X g\left(y\right)\in X g(y)∈X使得
f ( g ( y ) ) = f ∘ g ( y ) = 1 X ( y ) = y f\left(g\left(y\right)\right) = f\circ g\left(y\right) = 1_X\left(y\right)=y f(g(y))=f∘g(y)=1X(y)=y
成立,故 f f f满射
充分性:若 f f f是满射,则构造 g g g如下:
g : Y → X , g ( y ) = x g:Y\to X,\\ g\left(y\right)=x g:Y→X,g(y)=x
则 g g g是函数。这是因为对于任意的 y ∈ Y y\in Y y∈Y,由于 f f f是满射,所以 f − 1 ( { y } ) f^{-1}\left(\left\{y\right\}\right) f−1({y})\neq \empty$,
从而有某唯一确定的 x ∈ f − 1 ( { y } ) ⊆ X x\in f^{-1}\left(\left\{y\right\}\right)\subseteq X x∈f−1({y})⊆X,使得 < y , x > ∈ g \left<y,x\right>\in g ⟨y,x⟩∈g
并且对于任意的 y ∈ Y y\in Y y∈Y,
f ∘ g ( y ) = f ( g ( y ) ) = f ( x ) = y = 1 Y ( y ) f\circ g\left(y\right) = f\left(g\left(y\right)\right) = f\left(x\right)=y=1_Y\left(y\right) f∘g(y)=f(g(y))=f(x)=y=1Y(y)
所以 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y,故 f f f是右可逆的
(3)先证 f f f是可逆的,则 f f f是双射
由于 f f f可逆的,所以有 g : Y → X g:Y\to X g:Y→X,使得 g ∘ f = 1 X g\circ f=1_X g∘f=1X且 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y成立
根据 1 X 1_X 1X是单射, f f f是单射;
根据 1 Y 1_Y 1Y是满射, f f f是满射,故 f f f是双射
再证 f f f是双射,则 f f f既是左可逆的,又是右可逆的
由于 f f f是双射,所以 f f f是单射,也是满射,根据(1)和(2)可知, f f f既是左可逆的,又是右可逆的
最后证明, f f f既是左可逆的,又是右可逆的 ,则 f f f是可逆的
由于 f f f左可逆,所以有 g 1 : Y → X g_1:Y\to X g1:Y→X,使得 g 1 ∘ f = 1 X g_1\circ f=1_X g1∘f=1X
由于 f f f右可逆,所以有 g 2 : Y → X g_2:Y\to X g2:Y→X,使得 f ∘ g 2 = 1 Y f\circ g_2=1_Y f∘g2=1Y
因此有
g 1 = g 1 ∘ 1 Y = g 1 ∘ ( f ∘ g 2 ) = ( g 1 ∘ f ) ∘ g 2 = 1 X ∘ g 2 = g 2 g_1=g_1\circ 1_Y = g_1\circ\left(f\circ g_2\right)=\left(g_1\circ f\right)\circ g_2=1_X\circ g_2 = g_2 g1=g1∘1Y=g1∘(f∘g2)=(g1∘f)∘g2=1X∘g2=g2
故有 g = g 1 = g 2 g=g_1=g_2 g=g1=g2,使得 g ∘ f = 1 X g\circ f=1_X g∘f=1X且 f ∘ g = 1 Y f\circ g=1_Y f∘g=1Y,由此可知 f f f是可逆的
定理4:双射函数的逆函数是唯一的
证明:设双射函数 f : X → Y f:X\to Y f:X→Y.若 f f f有逆函数 g 1 g_1 g1和 g 2 g_2 g2,那么
g 1 = g 1 ∘ 1 Y = g 1 ∘ ( f ∘ g 2 ) = ( g 1 ∘ f ) ∘ g 2 = 1 X ∘ g 2 = g 2 g_1=g_1\circ 1_Y=g_1\circ \left(f\circ g_2\right)=\left(g_1\circ f\right)\circ g_2=1_X\circ g_2=g_2 g1=g1∘1Y=g1∘(f∘g2)=(g1∘f)∘g2=1X∘g2=g2
故逆函数是唯一的
定理5:设 f : X → Y , g : Y → Z f:X\to Y,g:Y\to Z f:X→Y,g:Y→Z,并且 f f f和 g g g都是可逆的 ,则
(1) ( f − 1 ) − 1 = f \left(f^{-1}\right)^{-1}=f (f−1)−1=f
(2) ( g ∘ f ) − 1 = f − 1 ∘ g − 1 \left(g\circ f\right)^{-1}=f^{-1}\circ g^{-1} (g∘f)−1=f−1∘g−1
证明:
(1)显然
(2)因 g ∘ f : X → Z g\circ f:X\to Z g∘f:X→Z,所以 ( g ∘ f ) − 1 : Z → X \left(g\circ f\right)^{-1}:Z\to X (g∘f)−1:Z→X,因 f − 1 : Y → X , g − 1 : Z → Y f^{-1}:Y\to X, g^{-1}:Z\to Y f−1:Y→X,g−1:Z→Y,所以 f − 1 ∘ g − 1 : Z → X f^{-1}\circ g^{-1}:Z\to X f−1∘g−1:Z→X
( f − 1 ∘ g − 1 ) ∘ ( g ∘ f ) = f − 1 ∘ ( g − 1 ∘ g ) ∘ f = f − 1 ∘ 1 Y ∘ f = f − 1 ∘ f = 1 X ( g ∘ f ) ∘ ( f − 1 ∘ g − 1 ) = g ∘ ( f ∘ f − 1 ) ∘ g − 1 = g ∘ 1 Y ∘ g − 1 = g ∘ g − 1 = 1 Z \left(f^{-1}\circ g^{-1}\right)\circ \left(g\circ f\right) = f^{-1}\circ \left(g^{-1}\circ g\right)\circ f=f^{-1}\circ 1_Y \circ f=f^{-1}\circ f=1_X\\ \left(g\circ f\right)\circ \left(f^{-1}\circ g^{-1}\right) = g\circ \left(f\circ f^{-1}\right)\circ g^{-1}=g\circ 1_Y\circ g^{-1}=g\circ g^{-1}=1_Z (f−1∘g−1)∘(g∘f)=f−1∘(g−1∘g)∘f=f−1∘1Y∘f=f−1∘f=1X(g∘f)∘(f−1∘g−1)=g∘(f∘f−1)∘g−1=g∘1Y∘g−1=g∘g−1=1Z
故 ( g ∘ f ) − 1 = f − 1 ∘ g − 1 \left(g\circ f\right)^{-1}=f^{-1}\circ g^{-1} (g∘f)−1=f−1∘g−1
课后习题
4.设 f : X → Y , g : Y → Z f:X\to Y, g:Y\to Z f:X→Y,g:Y→Z.若 g ∘ f g\circ f g∘f是可逆的,则 f f f和 g g g一定是左可逆的吗?为什么?
证明:
f f f单射, g g g不一定
因为 g ∘ f g\circ f g∘f是左可逆的,所以 g ∘ f g\circ f g∘f单射,所以 f f f单射
构造思路:有限集合的情况的时候,单射 ∣ X ∣ ≤ ∣ Y ∣ \left|X\right|\le \left|Y\right| ∣X∣≤∣Y∣
那么现在 ∣ X ∣ ≤ ∣ Y ∣ , ∣ X ∣ ≤ ∣ Z ∣ \left|X\right|\le \left|Y\right|, \left|X\right|\le \left|Z\right| ∣X∣≤∣Y∣,∣X∣≤∣Z∣
只要构造一个 ∣ Y ∣ > ∣ Z ∣ \left|Y\right|>\left|Z\right| ∣Y∣>∣Z∣
设 f ( x 1 ) = y 1 , f ( x 2 ) = y 2 f\left(x_1\right)=y_1,f\left(x_2\right)=y_2 f(x1)=y1,f(x2)=y2
g ( y 1 ) = z 1 , g ( y 2 ) = g ( y 3 ) = z 2 g\left(y_1\right)=z_1, g\left(y_2\right)=g\left(y_3\right)=z_2 g(y1)=z1,g(y2)=g(y3)=z2
由于 g g g不是单射,所以 g g g不是单射
5.设 f : X → Y , ∣ X ∣ ≥ 2 f:X\to Y,\left|X\right|\ge 2 f:X→Y,∣X∣≥2.证明: f f f是可逆的当且仅当 f f f有唯一的左(右)逆函数
证明:
必要性: f f f是可逆的
因此 f f f双射,进而 f f f左可逆且右可逆
设左逆函数 g 1 , g 2 : Y → X g_1,g_2:Y\to X g1,g2:Y→X,且 g 1 ∘ f = g 2 ∘ f = 1 X g_1\circ f=g_2\circ f=1_X g1∘f=g2∘f=1X
右逆函数 h : Y → X , f ∘ h = 1 Y h:Y\to X, f\circ h = 1_Y h:Y→X,f∘h=1Y
则
g 1 = g 1 ∘ 1 Y = g 1 ∘ ( f ∘ h ) = ( g 1 ∘ f ) ∘ h = 1 X ∘ h = h g_1=g_1\circ 1_Y=g_1\circ \left(f\circ h\right)=\left(g_1\circ f\right)\circ h=1_X\circ h=h g1=g1∘1Y=g1∘(f∘h)=(g1∘f)∘h=1X∘h=h
同理, g 2 = h g_2=h g2=h,因此 g 1 = g 2 g_1=g_2 g1=g2
f f f有唯一的左逆函数
右逆函数同理
充分性:
1. f f f有唯一左逆函数
因为 f f f左可逆,因此 f f f单射
假设 f f f不满射,则 ∃ a ∈ Y , ∀ x ∈ X , f ( x ) ≠ a \exists a\in Y, \forall x\in X,f\left(x\right)\neq a ∃a∈Y,∀x∈X,f(x)=a
构造左逆函数 g 1 , g 2 : Y → X g_1,g_2:Y\to X g1,g2:Y→X
使得
g 1 ( a ) = x 1 g 2 ( a ) = x 2 x 1 , x 2 ∈ X , x 1 ≠ x 2 g_1\left(a\right)=x_1\\ g_2\left(a\right)=x_2\\ x_1,x_2\in X, x_1\neq x_2 g1(a)=x1g2(a)=x2x1,x2∈X,x1=x2
显然 g 1 ∘ f = g 2 ∘ f = 1 X g_1\circ f=g_2\circ f=1_X g1∘f=g2∘f=1X
与唯一左逆函数矛盾
因此 f f f满射
2. f f f有唯一右逆函数
因为 f f f右可逆,因此 f f f满射
假设 f f f不单射,即 ∃ x 1 , x 2 ∈ X , x 1 ≠ x 2 , f ( x 1 ) = f ( x 2 ) = y ∈ Y \exists x_1,x_2\in X, x_1\neq x_2,f\left(x_1\right)=f\left(x_2\right)=y \in Y ∃x1,x2∈X,x1=x2,f(x1)=f(x2)=y∈Y
构造右逆函数 h 1 , h 2 : Y → X h_1,h_2:Y\to X h1,h2:Y→X
使得
h 1 ( y ) = x 1 h 2 ( y ) = x 2 h_1\left(y\right)=x_1\\ h_2\left(y\right)=x_2 h1(y)=x1h2(y)=x2
显然 f ∘ h 1 = f ∘ h 2 = 1 Y f\circ h_1= f\circ h_2=1_Y f∘h1=f∘h2=1Y
与唯一右逆函数矛盾
因此 f f f单射
综上, f f f双射,进而 f f f可逆
参考:
离散数学(刘玉珍)
相关文章:

逆函数学习
逆函数 给定关系 R ⊆ X Y R\subseteq X\times Y R⊆XY,颠倒 R R R的所有有序偶可以得到 R R R的逆关系 R ~ ⊆ Y X \tilde{R}\subseteq Y\times X R~⊆YX 但是对于函数 f : X → Y f:X\to Y f:X→Y而言,其逆关系 f ~ \tilde{f} f~可能不是 Y Y Y到…...

代码审计——SSRF详解
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 漏洞描述02 审计要点03 漏洞特征04 漏洞案例05 修复方案 01 漏洞描述 服务端请求伪造攻击(SSRF)也成为跨站点端口攻击,是由于一些应用在向第三方主机请求资源时提…...
搭建Scala开发环境
一、Windows上安装Scala 1、到Scala官网下载Scala Scala2.13.10下载网址:https://www.scala-lang.org/download/2.13.10.html 单击【scala-2.13.10.msi】超链接,将scala安装程序下载到本地 2、安装Scala 双击安装程序图标,进入安装向导&…...
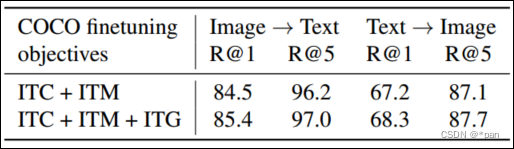
BLIP和BLIP2
文章主要是对BLIP2 (使用冻结图像编码器和大型语言模型的Bootstrapping语言图像预训练)论文的阅读笔记,也对BLIP(用于统一视觉语言理解和生成的Bootstrapping语言图像预训练)算法进行了简单的介绍。 文章:…...

微信小程序开发实战 ⑨(TabBar)
作者 : SYFStrive 博客首页 : HomePage 📜: 微信小程序 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 Ǵ…...
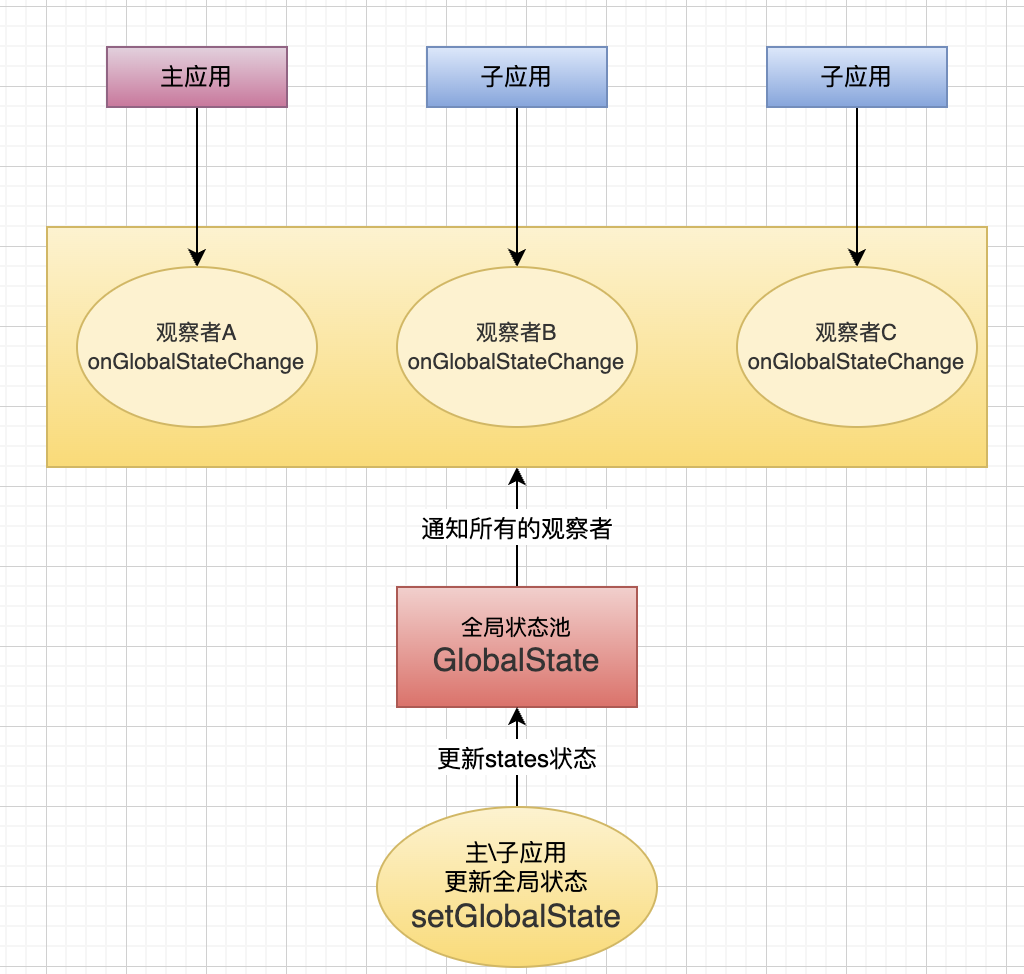
微前端探秘:初始微前端、现有方案和未来趋势
初识微前端 微前端是什么 概念: 微前端是指存在于浏览器中的微服务。 微前端是一种类似于微服务的架构,它将微服务的理念应用于浏览器端,即将单页面前端应用由单一的单体应用转变为把多个小型前端应用聚合为一体的应用。这就意味着前端应用…...

运维(SRE)成长之路-第2天 文本编辑工具之神VIM
vi和vim简介 在Linux中我们经常编辑修改文本文件,即由ASCII, Unicode 或其它编码的纯文字的文件。之前介绍过nano,实际工作中我们会使用更为专业,功能强大的工具 文本编辑种类: 全屏编辑器:nano(字符工具…...

45从零开始学Java之详解static修饰符、静态变量和静态方法
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦 千锋教育高级教研员、CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者 前言 在前一篇文章中,壹哥给大家讲解了abstract关键字,从而我们掌握了抽象类与抽象…...

电商超卖,从业务到设计
编辑导语:超卖这一概念的定义可以从不同层面进行阐述,比如平台层面、渠道层面、仓库层面等。而假设因超卖导致订单难以履行,则容易让用户体验“打折”。为什么有时电商超卖的现象会发生?可以从哪些角度来降低超卖导致的风险&#…...
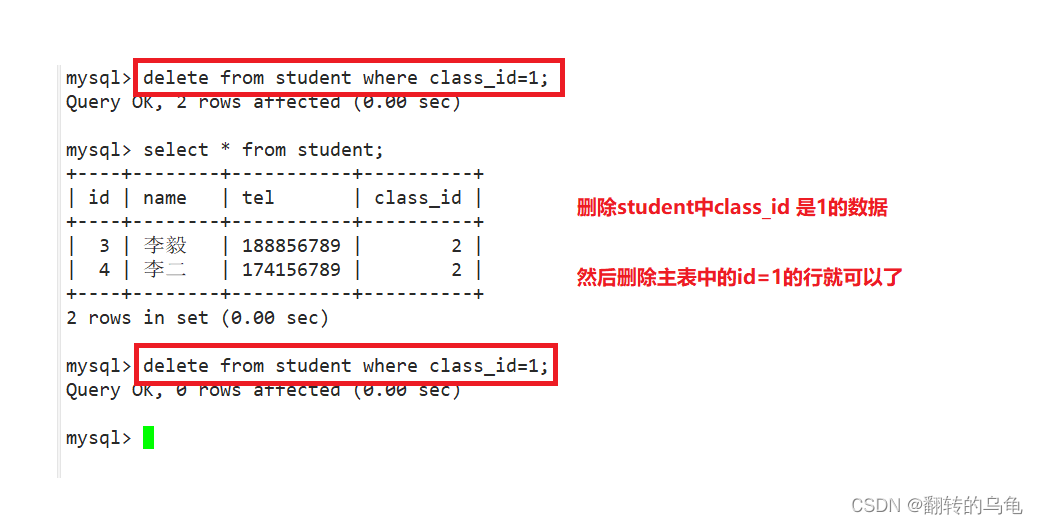
【MySQL】表的约束
表的约束 表的约束1. 空属性2. 默认值3. 列描述4. zerofill(自动补零)5. 主键—primary key5.1 复合主键 6. 自增长—auto_increment7.唯一键 --- unique8. 外键 --- foreign key…reference9. 综合案例 表的约束 真正约束字段的是数据类型,…...

【计算机网络】第一章 概述(下)
文章目录 第一章 概述1.5 计算机网络的性能指标1.5.1 速率1.5.2 带宽1.5.3 吞吐量1.5.4 时延 1.6 计算机网络体系结构1.6.1 常见的体系结构1.6.2 分层的必要性1.6.4 体系结构中的专用术语 1.8 习题 第一章 概述 1.5 计算机网络的性能指标 常用的 计算机网络 的性能指标有以下 …...

化工园区人员全过程轨迹化安全解决方案
1、项目背景 化工园区化工厂是生产安全重点单位,对人员定位管理需求强烈。对人员定位主要需求是:一般区域人数统计、人员轨迹、重点区域人员实时精准定位。 华安联大安全化工园区人员全过程轨迹化安全解决方案通过人员实时定位管理、移动轨迹追溯、险情…...

Java泛型中的T、E、K、V、?通配符,你确定都了解吗?
目录 前言 泛型带来的好处 泛型中通配符 小结 前言 Java 泛型(generics)是 JDK 5 中引入的一个新特性, 泛型提供了编译时类型安全检测机制,该机制允许开发者在编译时检测到非法的类型。 泛型的本质是参数化类型,也就是说所操…...
Jenkins部署及使用
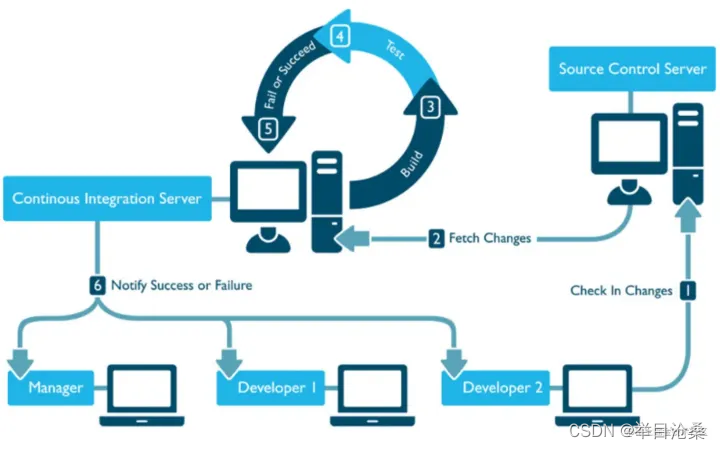
Jenkins 1.定义 1.Jenkins是一款开源CI/CD软件,用于自动化各种任务,包括构建、测试和部署软件 1.CI/CD 1.CI:持续集成(Continuous Integration) 1.协同开发是目前主流的开发方式,一般由多位开发人员同时处理同一个应用的不同模块…...

UML类图(二)
相信希望,相信自己 上一章简单介绍了 设计模式的原则(一), 如果没有看过,请观看上一章 本文参考文章: 常见UML符号详解 UML (Unified modeling language) 统一建模语言,是一种用于软件系统分析和设计的语言工具, 它用于帮助软件开发人员进行…...

【IoU全总结】GIoU, DIoU, CIoU, EIoUFocal, αIoU, SIoU,WIoU【基础收藏】
🥑 Welcome to Aedream同学 s blog! 🥑 并不存在效果一定优秀的IoU,需要结合自己的网络、数据集试验。 不想深究原理可直接跳转总结。文内公式均为手打,非图片,方便查看 文章目录 L1 Loss,L2Loss࿰…...

docker 安装 mysql
第一步,安装docker ,确保centos环境符合要求,有网 yum install docker -y 第二步:拉取mysql 首先可以先查询支持的mysql: search # 拉取镜像 docker pull mysql # 或者 docker pull mysql:latest # 以上两个命令是一致的&…...

Java 流程控制之 for 循环
Java语言中的for循环是一种常用的循环结构,用于重复执行一段代码,直到指定的条件不再成立。在本篇博客中,我们将深入探讨Java中的for循环,包括其语法、用法和示例。 一、for循环的基本语法 for循环的基本语法如下: …...
Kubernetes那点事儿——暴露服务之Ingress
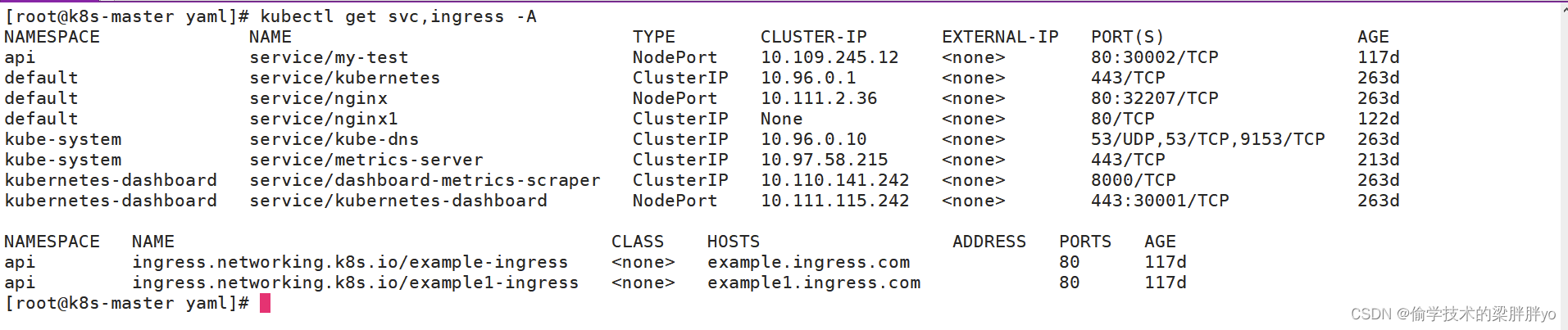
Kubernetes那点事儿——暴露服务之Ingress 前言一、ingress负载均衡器Ingress Controller路由规则Ingress 二、Ingress Controller三、案例 前言 在 k8s 集群中,如果我们将服务暴露出来,提供访问,可以使用Nodeport方式,但是Nodepo…...
八股文总结
文章目录 项目介绍1.不动产项目项目难点机器学习算法调研图像提取算法调研数据集-ImageNetXceptionVGGInceptionDensenetMobilenet 系统流程图 2.图书项目技术栈ShiroMybatisMyBatis:Mybatis Plus: 面试问题 Java基础基本数据类型反射接口和抽象类异常代理模式1. 静态代理2. 动…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
