编程的实践理论 第九章 交互
第九章 交互
根据状态的初始值和终止值,我们已经描述了计算。一个状态变量的声明如下:
var x: T· S = ∃x, x′: T· S
它说的是一个状态变量有两个数学变量,一个是初始值,一个是终止值。在这个
声明的作用域内,x和x'是在规格S中可用的。当这是一个依赖性的组合时,有
中间的变量值,但是这种中间值对于依赖性的组合的定义是本地化的。
P. Q = ∃x′′, y′′, ...· 〈x′, y′, ...→P〉 x′′ y′′ ... ∧ 〈x, y, ...→Q〉 x′′ y′′ ...
考虑 (P. Q) || R 。 在独立的组合中,在P和Q之间的中间值是隐藏的,
对于 R是不可见的,所以它们不能够用于进程的交互。
一个变量仅是初始值和终止值是可见的,叫做一个边界变量,一个变量的
所有的值都是可见的,叫做交互变量。所以,我们的变量都是边界的变量。
现在我们引入了交互变量,它的中间值对并行进程是可见的。这些变量用于
描述和推理人和计算机之间的交互,还有一个计算过程中的进程之间的交互。
9.0 交互的变量
令记号 ivar x: T· S 声明x为一个类型为T,作用域为S的交互变量。
它的定义如下:
ivar x: T· S = ∃x: time→T· S
时间是域的时间,或者是扩展的整数或者是扩展的实数。一个交互的变量
是一个时间的函数。变量x的值在时间t处是x t。
假定a和b是边界变量,x和y是交互变量,t是时间。对于独立的组合,我们
分区了所有的状态变量,边界变量和交互变量。假定 a 和 x 属于P,b和y
属于Q。
P||Q = ∃tP, tQ· 〈t′→P〉 tP ∧ (∀t′′· tP≤t′′≤t′ ⇒ xt′′=x(tP))
∧ 〈t′→Q〉 tQ ∧ (∀t′′· tQ≤t′′≤t′ ⇒ yt′′=y(tQ))
∧ t′ = max tP tQ
新的部分说,当短的进程被完成了,它的交互变量保留不变,直到长的进程完成了。
在如同之前的图,使用相同的进程和变量,赋值语句 x:= a+b+x+y 在进程P中,变量x
赋值为四个变量的和。因为a和x是进程P的变量,它们的值由进程P赋值最新的值,如果
没有进程P给这些变量赋值,这些变量保持初始值。因为b是进程Q的边界变量,它的值
在进程P中可以看到它的初始值,无论Q是否给它赋值。因为y是进程Q中一个交互变量,
它的值在进程P中可以看到,是由进程Q赋值的最新的值,或者是Q没有赋值的初始值,
或者是不知道。因为x是一个交互变量,它的新值在所有的并行的进程中可以看到。
表达式a+b+x+y 是一个有混淆的记号,因为a和b是数值,x和y 是从时间到数值的函数,
数值实际上被赋值为 a+b+xt+yt,但是当上下文清楚时,我们忽略了实际参数t。
我们将相似的写着x' 意味着 xt' ,x''意味着xt''。
ok的定义说边界变量和时间没有改变。所以之前的两个图中,在进程P中,
ok = a′=a ∧ t′=t
当含义是xt'=xt ,因为t'=t, 我们不需要说 x'=x。我们没有提及b和y ,
因为它们不是进程P的变量。
对交互变量的赋值,不能被实例化,因为它是时间来区别它的值。
在一个进程中,当一个边界变量是a和b,交互变量是x和y,
x:= e = a′=a ∧ b′=b ∧ x′=e ∧ (∀t′′· t≤t′′≤t′ ⇒ y′′=y)
∧ t′ = t+(要求评估和存储 e的时间 )
在对x的赋值其间,交互式变量y保留不变。在赋值期间关于x的值没有说。
如果我们愿意的话,对一个边界变量的赋值可以实例化。如果我们选择了对
时间的计量,我们必须说在赋值期间,所有的交互式变量都保持了不变。
依赖性的组合隐藏了边界变量和时间变量的中间值,只有交互式变量的中间
值是可见的。在边界变量a和b,交互式变量x和y,时间t, 我们定义
P. Q = ∃a′′, b′′, t′′· 〈a′, b′, t′→P〉 a′′ b′′ t′′ ∧ 〈a, b, t→Q〉 a′′ b′′ t′′
规格定律和推导定律的绝大部分,保留了交互式变量的可加性,但是很可惜的是,
替换定律不再是有效的。
如果P和Q是并行的,它们有不同的变量。再假定边界变量a和交互式变量x是进程P
的变量,边界变量b和交互式变量y是Q进程的变量。在规格P中,输入是a,b,xt,yt'',
条件是 t<=t''<t'。在规格P中,输出是a' 和 xt'' ,规格P是可实现的,条件如下:
∀a, b, X, y, t· ∃a′, x, t′· P ∧ t≤t′ ∧ ∀t′′· t<t′′≤t′ ∨ x t′′=X t′′
正如之前的,P必须被满足,没有非减时间,新的部分说,P必须不包括t到t'之间外的
交互式变量。我们不需要知道一个进程的规格的上下文,来检查它的可实现性;变量
b 和 y 仅出现在通用量词之外。
练习448号是一个例子,它有相同的变量,a,b,x,y,t。假定时间是一个扩展的整数,每
一次赋值花费时间 为1.
(x:= 2. x:= x+y. x:= x+y) || (y:= 3. y:= x+y) x是左边进程的变量,y是右边进程的变量
a在左边进程,b是右边进程
= (a′=a ∧ xt′=2 ∧ t′=t+1. a′=a ∧ xt′= xt+yt ∧ t′=t+1. a′=a ∧ xt′= xt+yt ∧ t′=t+1)
|| (b′=b ∧ yt′=3 ∧ t′=t+1. b′=b ∧ yt′= xt+yt ∧ t′=t+1)
= (a′=a ∧ x(t+1)=2 ∧ x(t+2)= x(t+1)+y(t+1) ∧ x(t+3)= x(t+2)+y(t+2) ∧ t′=t+3)
|| (b′=b ∧ y(t+1)=3 ∧ y(t+2)= x(t+1)+y(t+1) ∧ t′=t+2)
= a′=a ∧ x(t+1)=2 ∧ x(t+2)= x(t+1)+y(t+1) ∧ x(t+3)= x(t+2)+y(t+2)
∧ b′=b ∧ y(t+1)=3 ∧ y(t+2)= x(t+1)+y(t+1) ∧ y(t+3)=y(t+2) ∧ t′=t+3
= a′=a ∧ x(t+1)=2 ∧ x(t+2)=5 ∧ x(t+3)=10
∧ b′=b ∧ y(t+1)=3 ∧ y(t+2)=y(t+3)=5 ∧ t′=t+3
因为我们每一个赋值花费时间为1,例子给出了锁步骤的同步的样子。
更加现实的是,不同的赋值花费不同的时间,可能规定了不确定性
的上界和下界。我们决定了时间策略,是确定性还是不确定性,是
离散的还是连续的,定义和理论保持不变。当然了,复杂的时间
导致了非常复杂的表达式,用来描述所有的可能的交互过程。如
果关于可能的行为,我们要知道仅仅是一部分事,而不是所有的事,
我们能用推导来代换方程,弱化了简化目的。编程有其它的方式:
我们开始于一个期望行为的规格,加强了编程的必要性。
相关文章:

编程的实践理论 第九章 交互
第九章 交互 根据状态的初始值和终止值,我们已经描述了计算。一个状态变量的声明如下: var x: T S ∃x, x′: T S 它说的是一个状态变量有两个数学变量,一个是初始值,一个是终止值。在这个 声明的作用域内,x和x…...

BSN全球技术创新发展峰会在武汉举办,“延安链”正式发布
原标题:《第二届BSN全球技术创新发展峰会在武汉成功举行》 6月9日,由湖北省人民政府指导,湖北省发展改革委、国家信息中心联合主办,中国移动、中国电信、中国联通、武汉市江汉区人民政府、区块链服务网络(BSN…...
8.4 IP地址与端口号
目录 IP地址 IP地址及编址方式 IP 地址及其表示方法 点分十进制记法举例 IP 地址采用 2 级结构 分类的 IP 地址 分类的 IP 地址 多归属主机 各类 IP 地址的指派范围 编辑 一般不使用的特殊的 IP 地址 编辑 分类的 IP 地址的优点和缺点 划分子网 无分类编址 CIDR 无…...

day56_springmvc
今日内容 零、 复习昨日 零、 复习昨日 一、JSON处理【重点】 springmvc支持json数据交互,但是自己本身没有对应jar,使用的是第三方Jackson,只需要导入对应依赖,springmvc即可使用 如果需要换用到FastJson 导入依赖配置文件中指定json转换的类型为FastJson本次课程没有替换,用的…...

SQL Server Management Studio (SSMS)下载,安装以及连接数据库配置
目录 (一)前言 (二)下载与安装 1. 下载 (1)下载地址 (2)SSMS对操作系统的要求 2. 安装 (1)存放下载好的安装包 (2) 双击进入安…...

go 错误 异常
自定义错误 Go语言中 错误使用内建的 error 类型表示, error类型是一个接口类型:定义如下: error 有一个 Error() 的方法‘所有实现该接口的类型 都可以当做一个错误的类型;Error()方法输入具体错误描述,在打印错误时…...

智慧加油站卸油作业行为分析算法 opencv
智慧加油站卸油作业行为分析系统通过opencvpython网络模型技术,智慧加油站卸油作业行为分析算法实现对卸油作业过程的实时监测。当现场出现卸油作业时人员离岗,打电话人员抽烟等违规行为,灭火器未正确摆放,明火和烟雾等异常状态&a…...
LiangGaRy-学习笔记-Day22
1、shell工具-tput 这个是tput bash工具 具体的操作如下: tput clear:清屏tput cup Y X 第Y行,第X列的位置 tput bold:字体加粗tput sgr0 : 重置命令tput setaf n n:代表数字0-7 0黑色1红色2绿色3黄色4蓝…...

数据库横表和竖表有什么区别
横表和竖表是描述数据库表结构的两种形式,它们之间的主要区别在于数据的组织方式和用途。 横表(宽表): 横表是一种常见的表结构,其特点是每一行数据包含所有相关属性,字段通常作为列出现。横表中的每行代表…...

哈希表--day1--基本理论介绍
文章目录 哈希表哈希函数哈希碰撞拉链法线性探测法 常见的三种哈希函数数组setmap 总结 哈希表 Hash table是根据关键码的值来直接进行访问的数据结构。 其实直白来讲其实数组就是一张哈希表,不过其索引是十分简单的,我们通过0来访问num[0],…...
基于OpenMV的疲劳驾驶检测系统的设计
一、前言 借助平台将毕业设计记录下来,方便以后查看以及与各位大佬朋友们交流学习。如有问题可以私信哦。 本文主要从两个方面介绍毕业设计:硬件,软件(算法)。以及对最后的实验结果进行分析。感兴趣的朋友们可以评论区…...

chatgpt赋能python:使用Python来寻找两个列表不同元素的方法
使用Python来寻找两个列表不同元素的方法 在编写Python程序时,我们经常需要比较两个列表的元素,找出它们之间的不同之处。在搜索引擎优化(SEO)方面,这种比较对于找出两个网站内容的差异也非常有用。在这篇文章中&…...
简单学生管理系统
简单学生管理系统(Java)_封奚泽优的博客-CSDN博客https://blog.csdn.net/weixin_64066303/article/details/130667107?spm1001.2014.3001.5501 转载请注明出处,尊重作者劳动成果。 目录 前期准备: 数据库的连接: 用户账号类:…...
图像金字塔
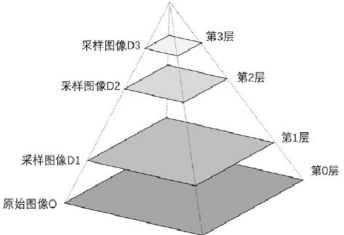
图像金字塔是由一幅图像的多个不同分辨率的子图构成的图像集合。是通过一个图像不断的降低采样率产生的,最小的图像可能仅仅有一个像素点。下图是一个图像金子塔的示例。从图中可以看到,图像金字塔是一系列以金字塔形状排列的、自底向上分辨率逐渐降低…...

Springboot整合Camunda工作流引擎实现审批流程实例
环境:Spingboot2.6.14 camunda-spring-boot-starter7.18.0 环境配置 依赖配置 <camunda.version>7.18.0</camunda.version> <dependency><groupId>org.camunda.bpm.springboot</groupId><artifactId>camunda-bpm-spring-boo…...
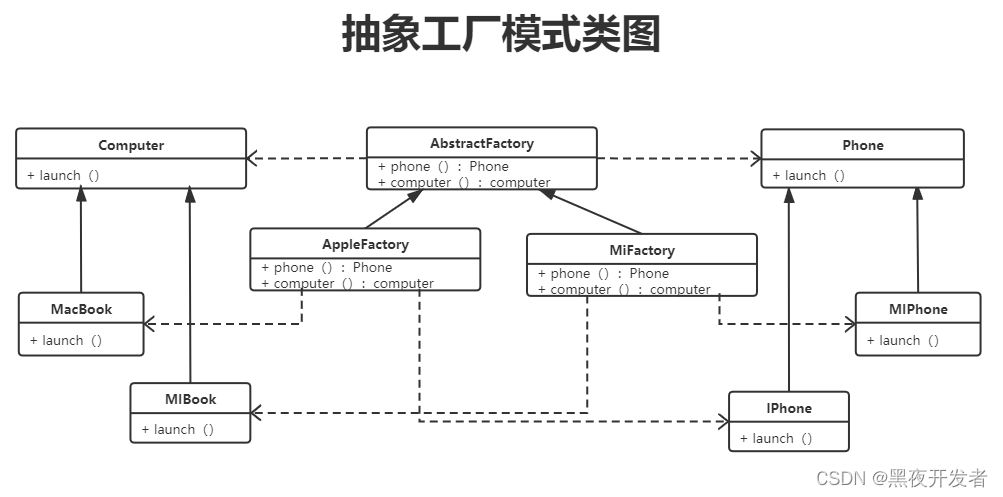
PHP设计模式21-工厂模式的讲解及应用
文章目录 前言基础知识简单工厂模式工厂方法模式抽象工厂模式 详解工厂模式普通的实现更加优雅的实现 总结 前言 本文已收录于PHP全栈系列专栏:PHP快速入门与实战 学会好设计模式,能够对我们的技术水平得到非常大的提升。同时也会让我们的代码写的非常…...

【玩转Docker小鲸鱼叭】理解Docker的核心概念
Docker核心概念 Docker有三大核心概念:镜像(Image)、容器(Container)、仓库(Repository) 1、镜像(Image) Docker镜像 是我们创建和运行Docker容器的基础,它…...

Eureka 心跳和服务续约源码探秘——图解、源码级解析
🍊 Java学习:社区快速通道 🍊 深入浅出RocketMQ设计思想:深入浅出RocketMQ设计思想 🍊 绝对不一样的职场干货:大厂最佳实践经验指南 📆 最近更新:2023年5月25日 🍊 点赞 👍 收藏 ⭐留言 📝 都是我最大的动力! 文章目录 分布式系统的心跳机制心跳机制的实…...

代码随想录二刷 530 二叉搜索树的最小绝对差 98. 验证二叉搜索树 700. 二叉搜索树中的搜索
530 二叉搜索树的最小绝对差 代码如下 func getMinimumDifference(root *TreeNode) int { var pre *TreeNode res : math.MaxInt var traverse func(root * TreeNode) traverse func(root * TreeNode) { if root nil { return } traverse(root.Left) …...
Docker安装——CentOS7.6(详细版)
ps:docker官网 在 CentOS 上安装 Docker 引擎 |官方文档 () 一、确定版本(必须是7以上版本) cat /etc/redhat-release 二、卸载旧版本(或者之前装过,没有安装过就不用管了) (root用…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
