代码随想录二刷 530 二叉搜索树的最小绝对差 98. 验证二叉搜索树 700. 二叉搜索树中的搜索
530 二叉搜索树的最小绝对差
代码如下
func getMinimumDifference(root *TreeNode) int {
var pre *TreeNode
res := math.MaxInt
var traverse func(root * TreeNode)
traverse = func(root * TreeNode) {
if root == nil {
return
}
traverse(root.Left) 定义两个指针,一个pre指针,一个为当前节点的root指针,因为是二叉搜索树,所以用中序遍历是递增序列
if pre != nil && root.Val - pre.Val < res { 当前一个节点不为空,那么比较前一个节点和当前节点的值,如果比之前的最小差值小,那么就更新最小差值
res = root.Val - pre.Val
}
pre = root 此时将pre指针更新,root指针指向下一个节点
traverse(root.Right)
}
traverse(root)
return res
}
func min(a,b int) int {
if a < b {
return a
}else {
return b
}
}
98. 验证二叉搜索树
代码如下
func isValidBST(root *TreeNode) bool {
var pre *TreeNode
var traverse func(root *TreeNode) bool
traverse = func(root *TreeNode) bool {
if root == nil { 如果是空节点也是二叉搜索树
return true
}
leftres := traverse(root.Left) 遍历左子树,并收集左子树的结果
if pre != nil && root.Val <= pre.Val { 因为用中序遍历二叉搜索树是一个升序序列。如果前一个节点比当前节点大,说明不是二叉搜索树
return false
}
pre = root 更新pre指针,并且root指向下一个节点
rightres := traverse(root.Right)
return rightres && leftres 返回左子树和右子树的结果
}
return traverse(root)
}
700. 二叉搜索树中的搜索
代码如下
func searchBST(root *TreeNode, val int) *TreeNode {
if root == nil || root.Val == val {
return root
}
if root.Val > val { 利用二叉搜索树的特点,如果当前节点值大于要找的值,则向当前节点的左子树寻找
return searchBST(root.Left,val)
}
return searchBST(root.Right,val) 如果当前节点的值小于要找的值,则向当前节点的右子树寻找
}
相关文章:

代码随想录二刷 530 二叉搜索树的最小绝对差 98. 验证二叉搜索树 700. 二叉搜索树中的搜索
530 二叉搜索树的最小绝对差 代码如下 func getMinimumDifference(root *TreeNode) int { var pre *TreeNode res : math.MaxInt var traverse func(root * TreeNode) traverse func(root * TreeNode) { if root nil { return } traverse(root.Left) …...
Docker安装——CentOS7.6(详细版)
ps:docker官网 在 CentOS 上安装 Docker 引擎 |官方文档 () 一、确定版本(必须是7以上版本) cat /etc/redhat-release 二、卸载旧版本(或者之前装过,没有安装过就不用管了) (root用…...
)
论信息系统项目的整体管理(范文)
论信息系统项目的整体管理(范文) 【摘要】 2016年10月,XX省卫生健康委启动了XX省分级转诊服务平台建设项目,我在项目中担任项目经理,负责项目的全面管理工作。该平台作为全省上下级医院转诊的信息化通道,…...

【音视频处理】音频编码AAC详解,低码率提高音质?
大家好,欢迎来到停止重构的频道。 本期我们介绍音频编码格式AAC。 AAC是音频最常用的编码格式之一,几乎所有的播放器都支持这个编码格式。 其他音频编码格式都是类似的,只是某些细节存在差别,如压缩算法、某些音频参数存在限制…...

逆函数学习
逆函数 给定关系 R ⊆ X Y R\subseteq X\times Y R⊆XY,颠倒 R R R的所有有序偶可以得到 R R R的逆关系 R ~ ⊆ Y X \tilde{R}\subseteq Y\times X R~⊆YX 但是对于函数 f : X → Y f:X\to Y f:X→Y而言,其逆关系 f ~ \tilde{f} f~可能不是 Y Y Y到…...

代码审计——SSRF详解
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 漏洞描述02 审计要点03 漏洞特征04 漏洞案例05 修复方案 01 漏洞描述 服务端请求伪造攻击(SSRF)也成为跨站点端口攻击,是由于一些应用在向第三方主机请求资源时提…...
搭建Scala开发环境
一、Windows上安装Scala 1、到Scala官网下载Scala Scala2.13.10下载网址:https://www.scala-lang.org/download/2.13.10.html 单击【scala-2.13.10.msi】超链接,将scala安装程序下载到本地 2、安装Scala 双击安装程序图标,进入安装向导&…...
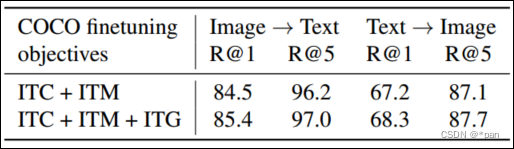
BLIP和BLIP2
文章主要是对BLIP2 (使用冻结图像编码器和大型语言模型的Bootstrapping语言图像预训练)论文的阅读笔记,也对BLIP(用于统一视觉语言理解和生成的Bootstrapping语言图像预训练)算法进行了简单的介绍。 文章:…...

微信小程序开发实战 ⑨(TabBar)
作者 : SYFStrive 博客首页 : HomePage 📜: 微信小程序 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 Ǵ…...
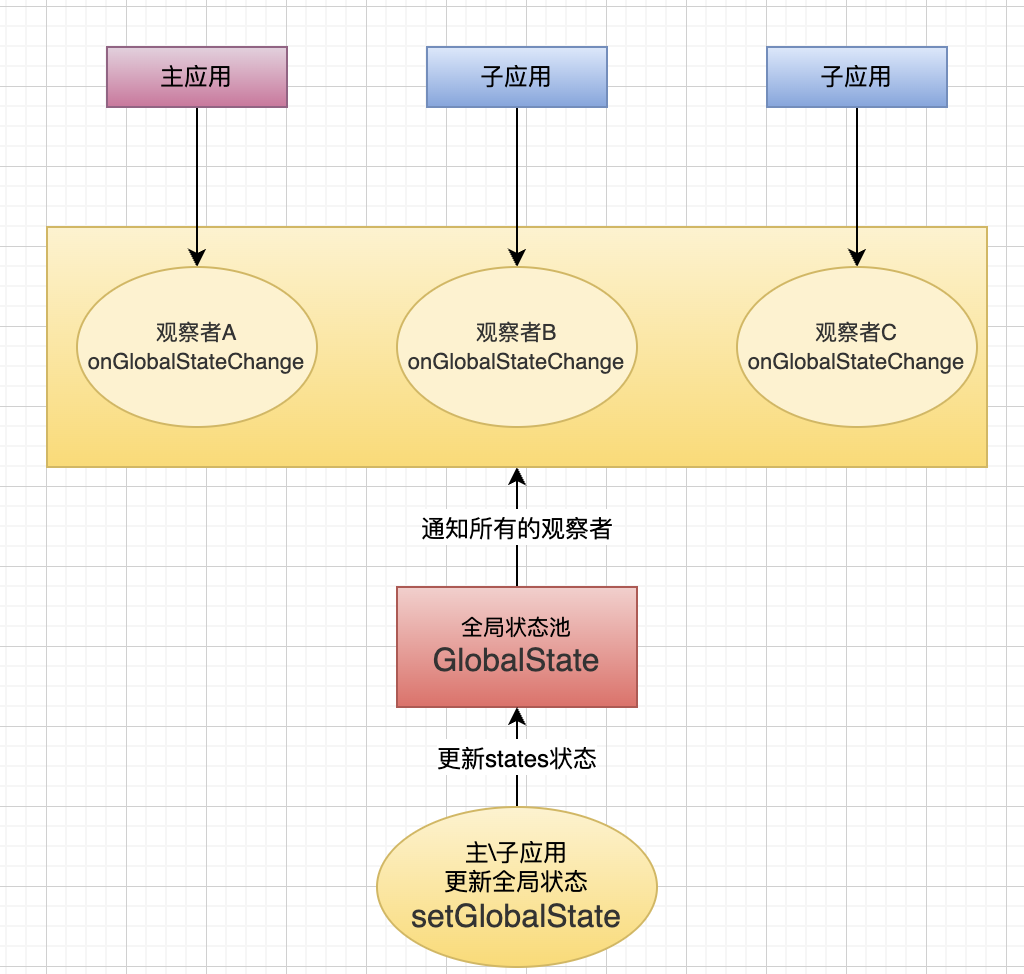
微前端探秘:初始微前端、现有方案和未来趋势
初识微前端 微前端是什么 概念: 微前端是指存在于浏览器中的微服务。 微前端是一种类似于微服务的架构,它将微服务的理念应用于浏览器端,即将单页面前端应用由单一的单体应用转变为把多个小型前端应用聚合为一体的应用。这就意味着前端应用…...

运维(SRE)成长之路-第2天 文本编辑工具之神VIM
vi和vim简介 在Linux中我们经常编辑修改文本文件,即由ASCII, Unicode 或其它编码的纯文字的文件。之前介绍过nano,实际工作中我们会使用更为专业,功能强大的工具 文本编辑种类: 全屏编辑器:nano(字符工具…...

45从零开始学Java之详解static修饰符、静态变量和静态方法
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦 千锋教育高级教研员、CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者 前言 在前一篇文章中,壹哥给大家讲解了abstract关键字,从而我们掌握了抽象类与抽象…...

电商超卖,从业务到设计
编辑导语:超卖这一概念的定义可以从不同层面进行阐述,比如平台层面、渠道层面、仓库层面等。而假设因超卖导致订单难以履行,则容易让用户体验“打折”。为什么有时电商超卖的现象会发生?可以从哪些角度来降低超卖导致的风险&#…...
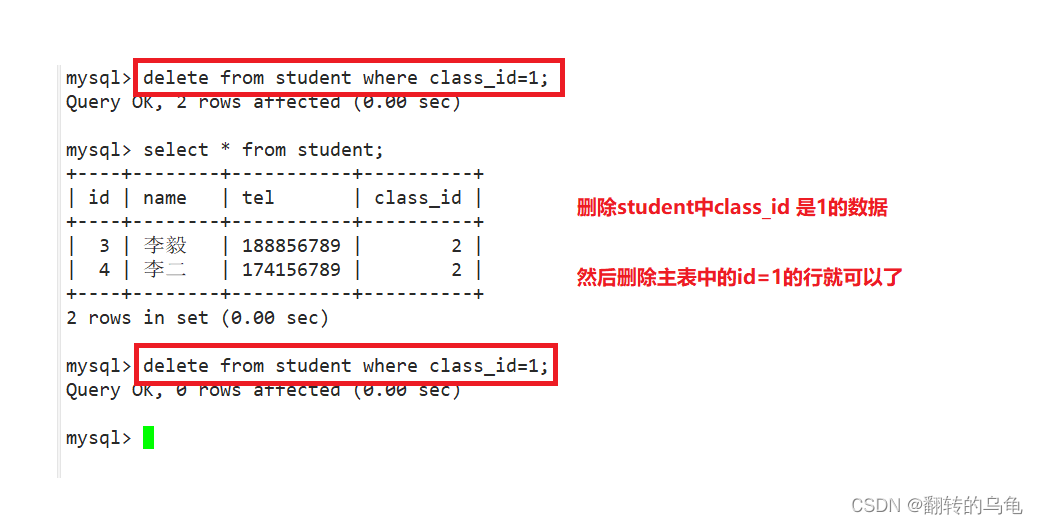
【MySQL】表的约束
表的约束 表的约束1. 空属性2. 默认值3. 列描述4. zerofill(自动补零)5. 主键—primary key5.1 复合主键 6. 自增长—auto_increment7.唯一键 --- unique8. 外键 --- foreign key…reference9. 综合案例 表的约束 真正约束字段的是数据类型,…...

【计算机网络】第一章 概述(下)
文章目录 第一章 概述1.5 计算机网络的性能指标1.5.1 速率1.5.2 带宽1.5.3 吞吐量1.5.4 时延 1.6 计算机网络体系结构1.6.1 常见的体系结构1.6.2 分层的必要性1.6.4 体系结构中的专用术语 1.8 习题 第一章 概述 1.5 计算机网络的性能指标 常用的 计算机网络 的性能指标有以下 …...

化工园区人员全过程轨迹化安全解决方案
1、项目背景 化工园区化工厂是生产安全重点单位,对人员定位管理需求强烈。对人员定位主要需求是:一般区域人数统计、人员轨迹、重点区域人员实时精准定位。 华安联大安全化工园区人员全过程轨迹化安全解决方案通过人员实时定位管理、移动轨迹追溯、险情…...

Java泛型中的T、E、K、V、?通配符,你确定都了解吗?
目录 前言 泛型带来的好处 泛型中通配符 小结 前言 Java 泛型(generics)是 JDK 5 中引入的一个新特性, 泛型提供了编译时类型安全检测机制,该机制允许开发者在编译时检测到非法的类型。 泛型的本质是参数化类型,也就是说所操…...
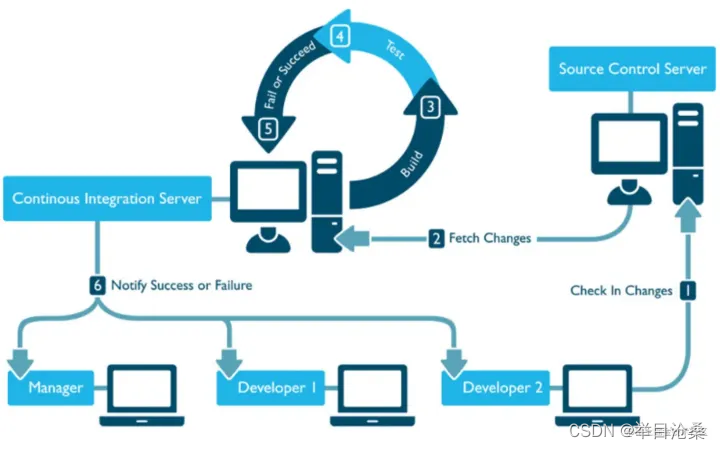
Jenkins部署及使用
Jenkins 1.定义 1.Jenkins是一款开源CI/CD软件,用于自动化各种任务,包括构建、测试和部署软件 1.CI/CD 1.CI:持续集成(Continuous Integration) 1.协同开发是目前主流的开发方式,一般由多位开发人员同时处理同一个应用的不同模块…...

UML类图(二)
相信希望,相信自己 上一章简单介绍了 设计模式的原则(一), 如果没有看过,请观看上一章 本文参考文章: 常见UML符号详解 UML (Unified modeling language) 统一建模语言,是一种用于软件系统分析和设计的语言工具, 它用于帮助软件开发人员进行…...

【IoU全总结】GIoU, DIoU, CIoU, EIoUFocal, αIoU, SIoU,WIoU【基础收藏】
🥑 Welcome to Aedream同学 s blog! 🥑 并不存在效果一定优秀的IoU,需要结合自己的网络、数据集试验。 不想深究原理可直接跳转总结。文内公式均为手打,非图片,方便查看 文章目录 L1 Loss,L2Loss࿰…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
