【蓝桥云课】求正整数的约数个数
一、求正整数n的约数个数
方法一(常用算法):从1到n逐一判断其能否整除n,若能整除n即为n的约数,否则不是n的约数。
方法二:从1到n\sqrt{n}n逐一判断是否为n的约数,当n\sqrt{n}n为n的约数时,个数加1;其余情况为约数时,个数加2。
方法三(素因子法):
对于任意整数n(n≥1),都可以写成唯一素因子乘积的形式,即 :
n=∏i=1kpiai=p1a1∗p2a2∗...∗pkakn=\prod_{i=1}^{k}p_i^{a_i}=p_1^{a_1}*p_2^{a_2}*...*p_k^{a_k}n=i=1∏kpiai=p1a1∗p2a2∗...∗pkak
,则n的约数个数为(a1+1)∗(a2+1)∗...∗(ak+1)(a_1+1)*(a_2+1)*...*(a_k+1)(a1+1)∗(a2+1)∗...∗(ak+1)
例如:36=2×2×3×3=22×322^2×3^222×32,36的约数个数为(2+1)×(2+1)=9
24=2×2×2×3=23×312^3×3^123×31,24的约数个数为(3+1)×(1+1)=8
import java.util.Scanner;public class FacOfNum {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while(sc.hasNext()) {int n = sc.nextInt();System.out.printf("%d的约数有%d个\n",n,f1(n));System.out.printf("%d的约数有%d个\n",n,f2(n));System.out.printf("%d的约数有%d个\n",n,syz(n));}}/*方法一:从1到n逐一遍历判断*/public static int f1(int n) {int cnt = 0;for(int i=1;i<=n;i++) {if(n%i==0) cnt++;}return cnt;}/*方法二:从1到√n逐一遍历判断*/public static int f2(int n) {int cnt = 0;for(int i=1;i*i<=n;i++) {if(n%i==0) {if(i*i==n) cnt++;else cnt+=2;}}return cnt;}/*方法三:素因子的方法*/public static int syz(int n) {int cnt = 1;int bak = n;for(int i=2;i*i<=bak;i++) {int num = 0;while(bak%i==0) {num++;bak=bak/i;}cnt =cnt*(num+1);}if(bak>1) cnt=cnt*(1+1);//n本身为素数的情况return cnt;}
}
二、100!约数的个数
方法:采用素因子的方法统计
import java.util.Scanner;public class Fac100 {public static void main(String[] args) {int n = 100;System.out.println(facofn(n));}public static long facofn(int n) {int[] prime = new int[n+1];//prime[i]表示素数i这个因子出现的个数for(int i=2;i<=n;i++) {int bak = i;for(int j=2;j*j<=bak;j++) {while(bak%j==0) {prime[j]++;//当前bak是能整除j,有素因子j,prime[j]计数器+1bak=bak/j;}}if(bak>1) prime[bak]++;}long ans = 1;for(int i=2;i<=n;i++) ans=ans*(prime[i]+1);return ans;}
}
相关文章:

【蓝桥云课】求正整数的约数个数
一、求正整数n的约数个数 方法一(常用算法):从1到n逐一判断其能否整除n,若能整除n即为n的约数,否则不是n的约数。 方法二:从1到n\sqrt{n}n逐一判断是否为n的约数,当n\sqrt{n}n为n的约数时,个数加1&…...

刷题记录: wannafly25 E 牛客NC19469 01串 [线段树维护动态dp]
传送门:牛客 题目描述: Bieber拥有一个长度为n的01 串,他每次会选出这个串的一个子串作为曲谱唱歌,考虑该子串从左 往右读所组成的二进制数P。 Bieber每一秒歌唱可以让P增加或减少 2 的 k次方(k由Bieber选 定),但必须…...
懂九转大肠的微软New Bing 内测申请教程
最近微软的New Bing开放内测了,网上已经有拿到内测资格的大佬们对比了ChatGPT和New Bing。对比结果是New Bing比ChatGPT更强大。来看看具体对比例子吧 1.时效性更强 ChatGPT的库比较老,跟不上时事,比如你问它九转大肠的梗,ChatG…...

WRAN翻译
基于小波的图像超分辨残差注意力网络 Wavelet-based residual attention network for image super-resolution 代码: https://github.com/xueshengke/WRANSR-keras 摘要: 图像超分辨率技术是图像处理和计算机视觉领域的一项基础技术。近年来,…...

ROS学习笔记——第二章 ROS通信机制
主要跟着[1]学习ros::Rate r(1); //错误,应改为ros::Rate r(10);[2]对Topic通信打的比方很形象,便于理解记忆。[3]有整个过程的图片,对于初学者更加友好[4]对发布者的代码注释非常好,方便进一步学习此外CMake官方文档可以查询相关…...
MacOS Pytorch 机器学习环境搭建
学习 Pytorch ,首先要搭建好环境,这里将采用 Anoconda Pytorch PyCharm 来一起构建 Pytorch 学习环境。 1. Anoconda 安装与环境创建 Anoconda 官方介绍:提供了在一台机器上执行 Python/R 数据科学和机器学习的最简单方法。 为什么最简单…...

项目——博客系统
文章目录项目优点项目创建创建相应的目录,文件,表,导入前端资源实现common工具类实现拦截器验证用户登录实现统一数据返回格式实现加盐加密类实现encrypt方法实现decrypt方法实现SessionUtil类实现注册页面实现前端代码实现后端代码实现登录页…...
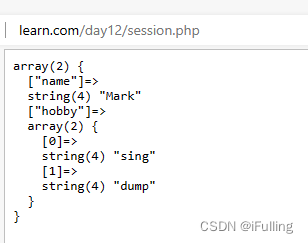
PHP(14)会话技术
PHP(14)会话技术一、概念二、分类三、cookie技术1. cookie的基本使用2. cookie的生命周期3. cookie的作用范围4. cookie的跨子域5. cookie的数组数据四、session1. session原理2. session基本使用3. session配置4. 销毁session一、概念 HTTP协议是一种无…...

对JAVA 中“指针“理解
对于Java中的指针,以下典型案例会让你对指针的理解更加深刻。 首先对于: 系统自动分配对应空间储存数字 1,这个空间被变量名称b所指向即: b ——> 1 变量名称 空间 明…...

功率放大器在MEMS微结构模态测试研究中的应用
实验名称:功率放大器在MEMS微结构模态测试研究中的应用研究方向:元器件测试测试目的:随着MEMS器件在各个领域中广泛应用,对微结构进行模态测试获得其动态特性参数对微结构的设计、仿真、制造、以及质量控制和评价等方面具有十分重…...
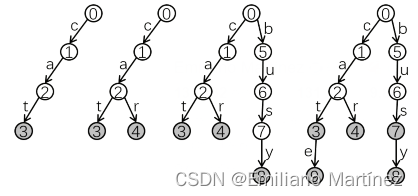
【算法基础】字典树(Trie树)
一、Trie树原理介绍 1. 基本概念 Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。【高效存储和查找字符串集合的数据结构】,存储形式如下: 2. 用数组来模拟Trie树的…...
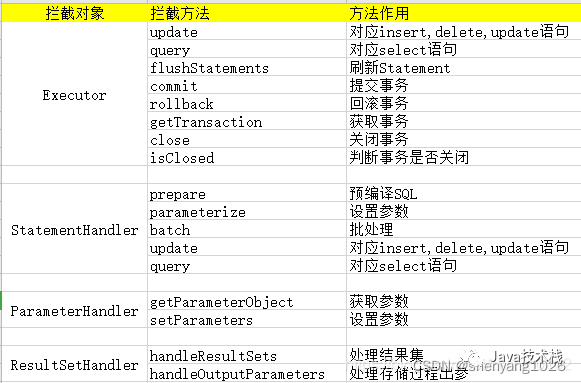
MyBatis 插件 + 注解轻松实现数据脱敏
问题在项目中需要对用户敏感数据进行脱敏处理,例如身份号、手机号等信息进行加密再入库。解决思路就是:一种最简单直接的方式,在所有涉及数据敏感的查询到对插入时进行密码加解密方法二:有方法一到出现对所有重大问题的影响&#…...
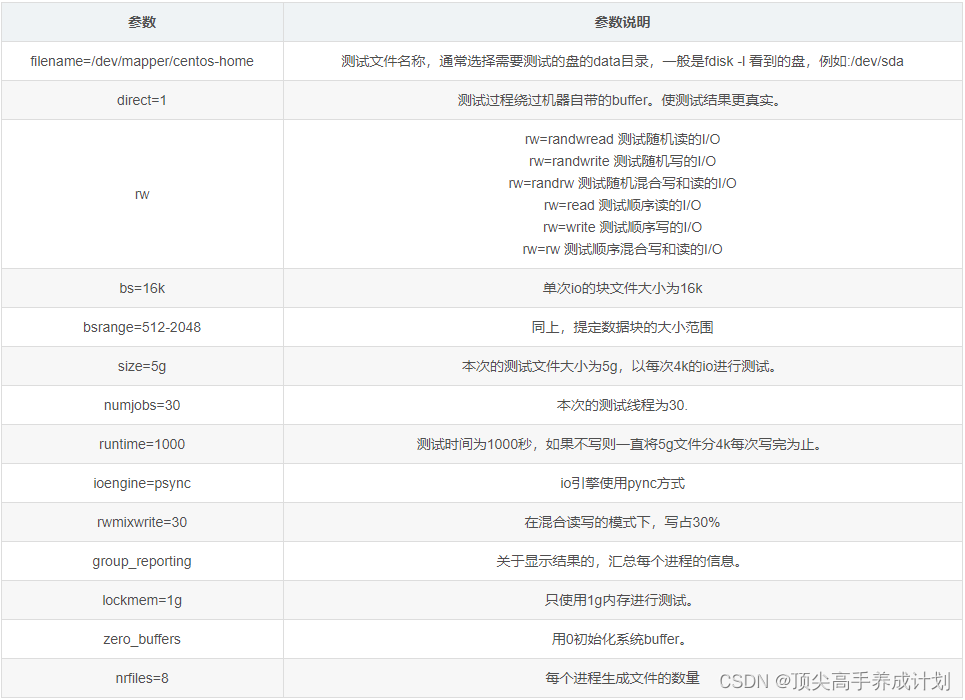
MySQL优化篇-MySQL压力测试
备注:测试数据库版本为MySQL 8.0 MySQL压力测试概述 为什么压力测试很重要?因为压力测试是唯一方便有效的、可以学习系统在给定的工作负载下会发生什么的方法。压力测试可以观察系统在不同压力下的行为,评估系统的容量,掌握哪些是重要的变化…...

CF43A Football 题解
CF43A Football 题解题目链接字面描述题面翻译题面描述题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1样例 #2样例输入 #2样例输出 #2代码实现题目 链接 https://www.luogu.com.cn/problem/CF43A 字面描述 题面翻译 题面描述 两只足球队比赛,现给你进…...

Nginx常用命令及具体应用(Linux系统)
目录 一、常用命令 1、查看Nginx版本命令,在sbin目录下 2、检查配置文件的正确性 3、启动和停止Nginx 4、查看日志,在logs目录下输入指令: 5、重新加载配置文件 二、Nginx配置文件结构 三、Nginx具体应用 1、部署静态资源 2、反向代…...

从零实现Web服务器(三):日志优化,压力测试,实战接收HTTP请求,实战响应HTTP请求
文章目录一、日志系统的运行流程1.1 异步日志和同步日志的不同点1.2 缓冲区的实现二、基于Webbench的压力测试三、HTTP请求报文解析http报文处理流程epoll相关代码服务器接收http请求四、HTTP请求报文响应一、日志系统的运行流程 步骤: 单例模式(局部静态变量懒汉…...
MFC入门
1.什么是MFC?全称是Microsoft Foundation Class Library,我们称微软基础类库。它封装了windows应用程序的各种API以及相关机制的C类库MFC是一个大的类库MFC是一个应用程序框架MFC类库常用的头文件afx.h-----将各种MFC头文件包含在内afxwin.h-------包含了各种MFC窗…...

1、H5+CSS面试题
1, HTML5中新增了哪些内容?广义上的html5指的是最新一代前端开发技术的总称,包括html5,CSS3,新增的webAPI。Html中新增了header,footer,main,nav等语义化标签,新增了video,audio媒体标签,新增了canvas画布。…...

亚马逊云科技重磅发布《亚马逊云科技汽车行业解决方案》
当今,随着万物智联、云计算等领域的高速发展,创新智能网联汽车和车路协同技术正在成为车企加速发展的关键途径,推动着汽车产品从出行代步工具向着“超级智能移动终端”快速转变。挑战无处不在,如何抢先预判?随着近年来…...
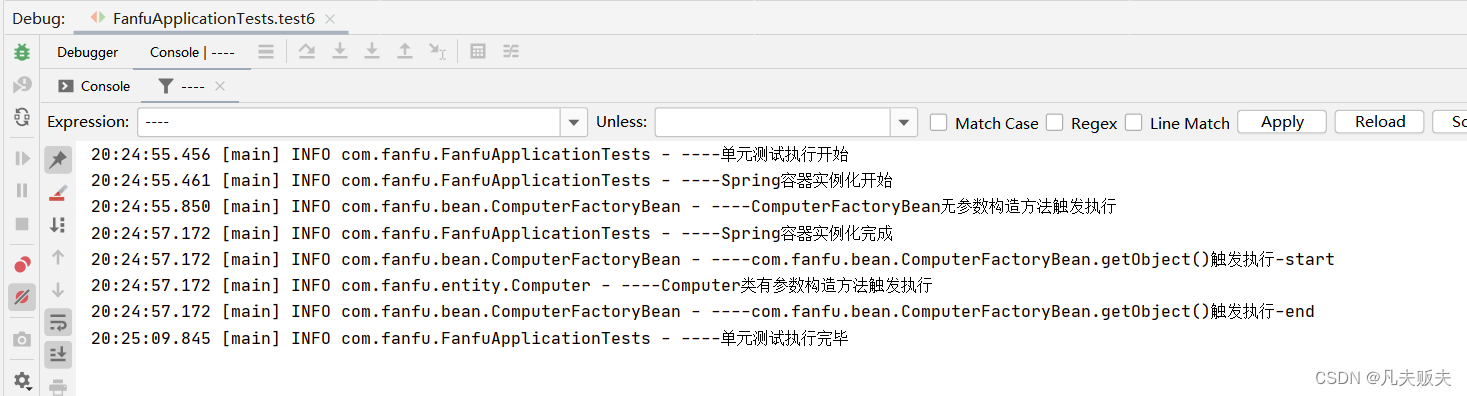
Springboot扩展点之FactoryBean
前言FactoryBean是一个有意思,且非常重要的扩展点,之所以说是有意思,是因为它老是被拿来与另一个名字比较类似的BeanFactory来比较,特别是在面试当中,动不动就问你:你了解Beanfactory和FactoryBean的区别吗…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
