数据结构与算法基础(青岛大学-王卓)(5)
叮叮咚咚,新一期来袭,我还在吃桃子,吃桃子,吃桃子。。。串和python的字符串差不多,数组和广义表像是python的list
文章目录
- 串(string) - 字符串
- 概念及术语
- 串的类型定义
- 存储结构(同线性表)
- 串的模式匹配算法
- BF 算法
- KMP算 法 (特点:速度快 )
- 数组
- 数组的定义
- 一维数组
- 二维数组
- 数组特点
- n维数组的数据类型定义
- 数组的顺序存储
- 特殊矩阵的压缩存储
- 对称矩阵
- 三角矩阵
- 对角矩阵
- 稀疏矩阵
- 广义表
- 概念
- 性质
- 广义表和线性表的区别?
- 基本运算
- 案例分析
- TO BE CONTINUED...
串(string) - 字符串
概念及术语
-
定义: 零个或多个任意字符组成的有限序列,是一种内容受限的线性表

-
子串 : 串中任意个连续字符组成的子序列称为该串的子串, 空串和串本身都是子串,不含本身的是真子串。
-
主串 : 包含子串的串相应地称为主串。
-
字符位置 : 字符在序列中的序号为该字符在串中的位置 。
-
子串位置 : 子串第一个字符在主串中的位置 。
-
空格串 : 由一个或多个空格组成的串 , 与空串不同。
-
串相等 : 当且仅当两个串的长度相等并且各个对应 位置上的字符都相同时 , 这两个串才是相等的 。
-
所有的空串是相等的。
串的类型定义


存储结构(同线性表)
-
顺序串(顺序存储结构)(更常用因不经常插入删除)
#define MAXLEN 255 typedef struct{char ch[MAXLEN+1]; // 存储串的一维数组,实际范围0-255(0可能保留不用)int length; // 串的当前长度长度 }SString; -
链串(链式存储结构)

// 块链结构 #define CHUNKSIZE 80 // 块的大小可有客户定义 typedef struct Chunk{char ch[CHUNKSIZE];struct Chunk *next; }Chunk;typedef struct LString{Chunk *head,*tail; // 串的头指针和尾指针int curlen; //串的当前长度 }LString; //字符串的块链结构
串的模式匹配算法
确定主串中所含子串(模式串)第一次出现的位置(BF&KMP)
BF 算法
- (Brute-Force, 又称古典的 、 经典的 、 朴素的 、 穷举的 )
思路:从主串的每一个字符开始依次与模式串字符进行比较
Index(S,T,pos)
-
将主串的第 pos 个字符和模式串的第一个字符比较 ,若相等,继续逐个比较后续字符;
-
若不等,从主串的下一字符起(回溯) , 重新与模式串的第一个字符比较
-
直到主串的一个连续子串字符序列与模式串相等。 返回值
为 S 中与 T 匹配的子序列第一个字符的序号 , 即匹配成功 。
否则 , 匹配失败 , 返回值 0
int Index_BF(SString S, SString T, int pos){int i=pos; j=1; // 主串i的位置从1开始pos>=1while(i<=S.length&&j<=T.length){ if (S.ch[i]==T.ch[j]) {++i; ++j;} // 主串和子串依次匹配下一个字符else {i=i-j+2; j=1} // 字符不相等,主串i回溯位置到(i-(j-1)+1),j回到1}if (j>T.length) return i-T.length; // 返回模式串匹配成功后主串对应首字符的下标else return 0; } -
时间复杂度为
(n-m)*m+m --> (n-m+1)*m--> O(n*m)(当m<<n)
KMP算 法 (特点:速度快 )
利用已经部分匹配的结果而加快模式串的滑动速度 ?
且主串 S 的指针 i 不必回溯 ! 可提速到 O( n+m )

j的位置可以根据模式串来确定 ,定义next[j]函数 , 表明当模式中剃个字符与主串中相应字符 " 失配 " 时 , 在模式中需重新和主串中该字符进行比较的字符的位置 。

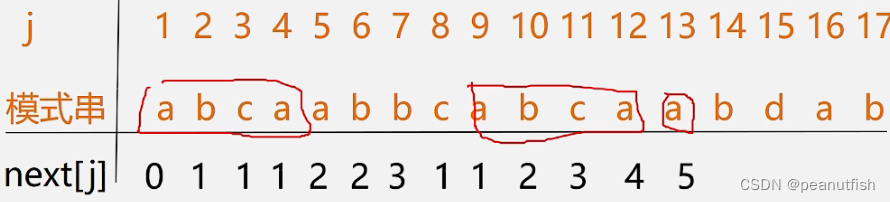
int Index_KMP(SString S, SString T, int pos){int i=pos; j=1; // 主串i的位置从1开始pos>=1while(i<=S.length&&j<=T.length){ if (S.ch[i]==T.ch[j]) {++i; ++j;} // 主串和子串依次匹配下一个字符else j=next[j] // 通过next[j]得到j的位置,i不用回溯}if (j>T.length) return i-T.length; // 返回模式串匹配成功后主串对应首字符的下标else return 0;
}void get_next(SString T, int &next[]){i=1; next[1]=0; j=0;while (i < T.length){if (j==0 || T.ch[i]==T.ch[j]){++i; ++j;next[i]=j;}else j=next[j];}
}
next[j]的改进- nextval[j]
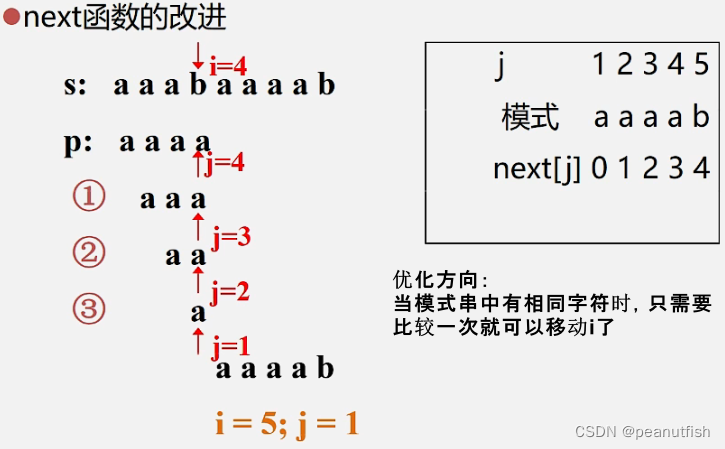

void get_nextval(SString T, int &nextval[]){i=1; nextval[1]=0; j=0;while (i < T.length){if (j==0 || T.ch[i]==T.ch[j]){++i; ++j;if (T.ch[i]==T.ch[j]) nextval[i]=j;else nextval[i]=nextval[j];}else j=nextval[j];}
}
数组
数组的定义
按一定格式排列起来的具有相同类型的数据元素的集合
一维数组
若线性表中的数据元素为非结构的简单元素,则称为一维数组 。
其逻辑结构有线性结构,定长的线性表 。
声明格式 : 数据类型 变量名称 [长度]
二维数组

声明格式: 数据类型变量名称 [行数] [列数] ,eg: int num[5][8]
在 C 语言中 ,一个二维数组类型也可以定义为一维数组类型
( 其分量类型为一维数组类型 ),
即 :typedef elemtype array2[m][n];
等价于 :
typedef elemtype array1[n];
typedef array1 array2[m];
三维数组 : 若二维数组中的元素又是一个一维数组 , 则称作三维数组 。。。。
n维数组:若n-1维数组中的元素又是一个一维数组结构则称为n维数组 。
线性表是数组结构的一个特例,数组结构又是线性表结构的扩展。
数组特点
结构固定(定以后维数和维界不再改变),基本操作就是初始化,销毁,取元素,修改元素 。
n维数组的数据类型定义


数组的顺序存储
一维数组存储位置

二维数组存储
-
以行优先 - JAVA, C, BASIC ,COBOL ,PASCAL

-
以列优先 - FORTRAN

三维数组 按页行列存放,页优先的顺序存储
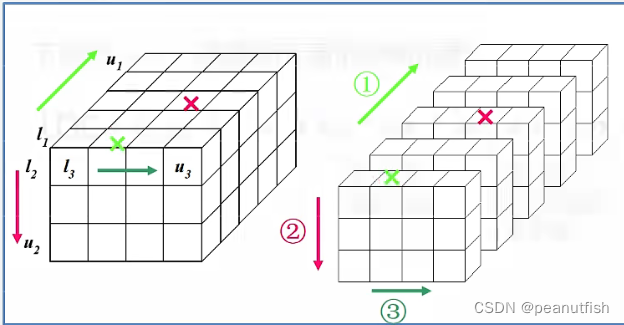

扩展到n维数组存储位置计算


特殊矩阵的压缩存储
-
压缩存储定义:若多个数据元素的值都相同 , 则只分配一个元素值的存储空间 , 且
零元素不占存储空间 。 -
特殊矩阵:对称矩阵,对角矩阵,三角矩阵,稀疏矩阵(非零元素个数一般<5%)
对称矩阵

只需存储一半元素,存储个数为每一行个数相加,即1+2+3+…+n=n(n+1)/2
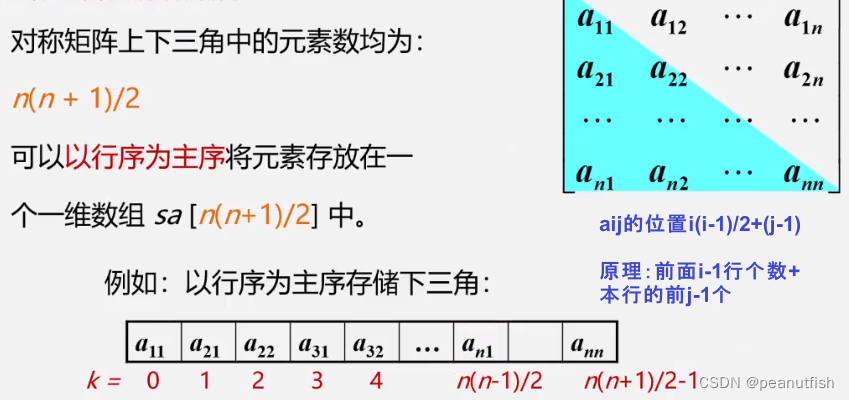
任一个元素存在一维数组的位置aij的位置i(i-1)/2+(j-1) 原理:前面(i-1)行个数+本行的前(j-1)个元素
三角矩阵

对角矩阵
[ 特点 ] 在n×n的方阵中,所有非零元素都集中在以主对角线为中心的带状区域中,区域外的值全为0 ,则称为对角矩阵 。 常见的有三对角矩阵 、 五对角矩阵 、 七对角矩阵等 。(3/5/7条数据)

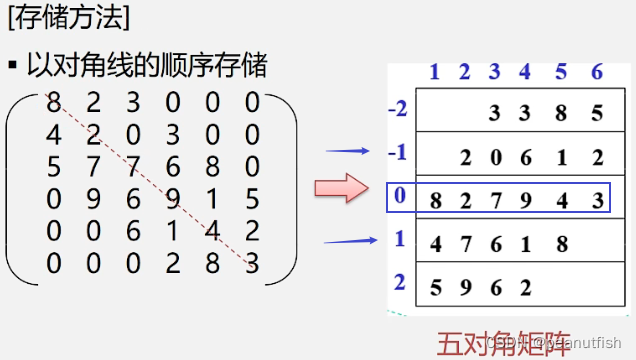
稀疏矩阵
三元组(行,列,值) 和矩阵维数(总行,总列)来唯一确定一个元素的位置

-
三元组顺序表又称有序的双下标法。
-
优点:非零元素在表中按行序有序存储
-
缺点:不能随机存储,按行号存取某一行中的非零元素要从头开始查找
十字链表 法存储稀疏矩阵
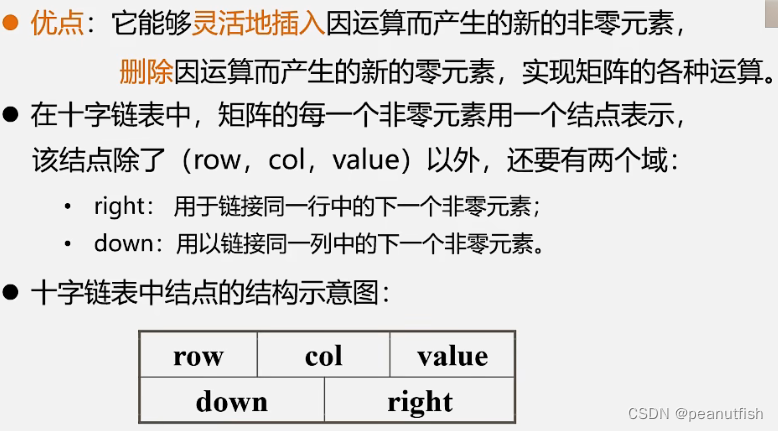
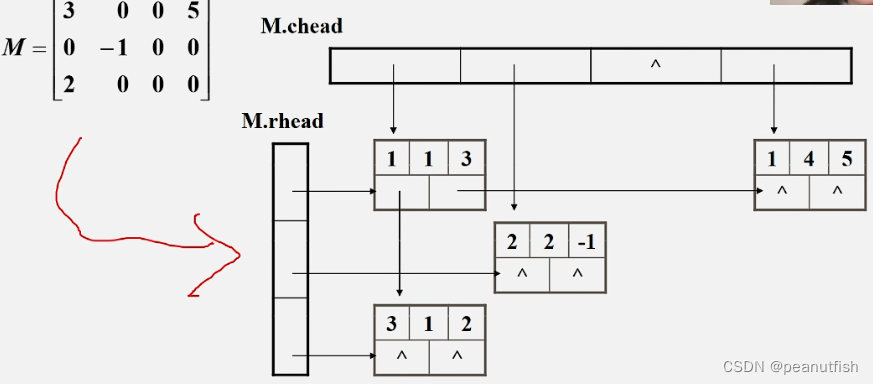
广义表
概念
广义表( 又称列表 Lists) 是 n>=0 个元素 a0, a1, a2…an-1的有限序列 , 其中每一个或者是原子 , 或者是一个广义表 。

性质


广义表和线性表的区别?
- 广义表是线性表的推广,线性表是广义表的特例
- 广义表的结构相当灵活 , 在某种前提下 , 它可以兼容线性表 、 数组 、
树和有向图等各种常用的数据结构 。
基本运算
GetHead(L): 求非空广义表的第一个元素,可以是一个原子或者一个子表
GetTail(L):非空广义表去掉表头元素以外其他元素所构成的表。
案例分析
病毒感染检测(病毒RNA是环状)
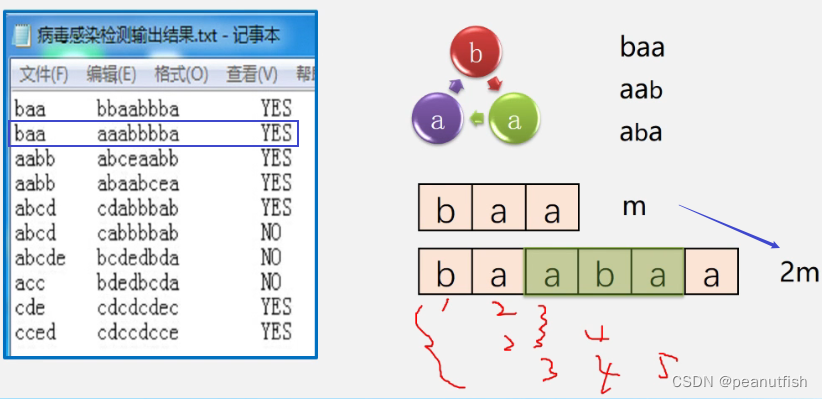
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tK0IY99o-1687358835821)(../resources/image-20230621224425435.png)]](https://img-blog.csdnimg.cn/b1091249707845e399005553c4372d80.png)
TO BE CONTINUED…
相关文章:

数据结构与算法基础(青岛大学-王卓)(5)
叮叮咚咚,新一期来袭,我还在吃桃子,吃桃子,吃桃子。。。串和python的字符串差不多,数组和广义表像是python的list 文章目录 串(string) - 字符串概念及术语串的类型定义存储结构(同线性表)串的模式匹配算法…...
微信小程序开发入门学习01-TDesign模板解读
目录 1 使用模板创建小程序2 app.json3 页面布局总结 原来我们使用微信开发者工具,比较困难的是前端框架的选择上,官方也没有提供一套框架供我们使用,最近开发者工具已经提供了一套前端框架,后续我们开发的效率会因为使用模板提高…...
使用 Jetpack Compose 创建自定义的对话框(Dialog)
在 Jetpack Compose 中,对话框(Dialog)是一种常见的用户界面组件,用于展示重要的信息、确认操作或者收集用户输入。本篇博客将带你深入了解 Jetpack Compose 中的对话框,并展示如何创建自定义的对话框,以满…...

c++ auto学习笔记
一、auto的意义 在C11中赋予auto的意义是:在声明变量时,根据初始化表达式自动推断该变量的类型。声明函数时作为函数返回值的占位符(用在函数返回类型后置的情况)。 如 auto i 6; //auto推断为intauto func()->int //函数返…...

【随机种子初始化】一个神经网络模型初始化的大坑
1 问题起因和经过 半年前写了一个模型,取得了不错的效果(简称项目文件1),于是整理了一番代码,保存为了一个新的项目(简称项目文件2)。半年后的今天,我重新训练这个整理过的模型&…...
翻过那座山——Gitlab流水线任务疑难之编译有子模块的项目指南
📢欢迎点赞 :👍 收藏 ⭐留言 📝 如有错误敬请指正,赐人玫瑰,手留余香!📢本文作者:由webmote 原创📢作者格言:新的征程,我们面对的不是…...

手机照片删除后如何恢复
在如今移动互联网和智能手机时代,拍摄照片已经成为了人们常见的一种生活方式,尤其是通过手机拍摄照片已经成为了许多人记录生活点滴、分享经验和表达情感等的必备工具。但是,随着手机照片量的激增,意外删除手机中珍贵照片的事件也…...
SpringBoot 线上服务假死,CPU 内存正常,什么情况?
背景 开发小伙伴都知道线上服务挂掉,基本都是因为cpu或者内存不足,出现GC频繁OOM之类的情况。本篇文章区别以上的情况给小伙伴们带来不一样的服务挂掉。 还记得哔哩哔哩713事故中那场诡计多端的0吗? 图片 对就是这个0,和本次事…...

kotlin从入门到精通之内置类型
基本类型 声明变量 val(value的简写)用来声明一个不可变的变量,这种变量在初始赋值之后就再也不能重新赋值,对应Java中的final变量。 var(variable的简写)用来声明一个可变的变量,这种变量在初始…...

实战指南:使用Spring Boot实现消息的发送和接收
当涉及到消息发送和接收的场景时,可以使用Spring Boot和消息中间件RabbitMQ来实现。下面是一个简单的示例代码,展示了如何在Spring Boot应用程序中创建消息发送者和接收者,并发送和接收一条消息。 首先,你需要进行以下准备工作 确…...

常用的数据结构——栈
目录 1、入栈 2、出栈 3、获取栈顶的元素 4、从栈中查找元素 栈是一种常见的数据结构,栈的特点是后进先出,就像我们叠盘子,拿走上面的盘子才能拿到下一个。java中的栈java.util.Stack是通过java.util.Vector实现的,所以底层都…...
C++完成淄博烧烤节管理系统
背景: 这次我们结合今年淄博烧烤做一个餐厅管理系统,具体需求如下,我们选择的是餐饮商家信息管理 问题描述: 淄博烧烤今年大火,“进淄赶烤”是大家最想干的事情,淄博烧烤大火特火的原因,火的…...

我心中的TOP1编程语言
目录 一、评选最佳编程语言时需要考虑哪些标准 (一)易用性 (二)执行效率 (三)语言功能特性 (四)工具生态环境 (五)开发者社区 二、不同编程语言的优点…...
)
Linux工具之gdb(含移植到arm-linux系统)
文章目录 文件目录结构移植ncurses库移植gdb移植到arm板调试测试 linux主机:ubuntu-18.04 交叉编译器:arm-buildroot-linux-gnueabihf 开发板kernel:Linux 5.4.0-150-generic x86_64 开发板:100ASK_STM32MP157_PRO开发板 arm-…...

DolphinScheduler
参考 Apache DolphinScheduler v1.3.9 使用手册 内置组件 masterserverworkserverzookeepertask queuealertapiui 设计 去中心化设计 通过zk选举 UI功能 队列管理 Yarn调度器的资源队列 用户管理 租户对应的是Linux系统用户,是Worker执行任务使用的用户 用户…...
10大白帽黑客专用的 Linux 操作系统
平时在影视里见到的黑客都是一顿操作猛如虎,到底他们用的都是啥系统呢? 今天给大家分享十个白帽黑客专用的Linux操作系统。 ▍1. Kali Linux Kali Linux是最著名的Linux发行版,用于道德黑客和渗透测试。Kali Linux由Offensive Security开发&…...

Golang每日一练(leetDay0099) 单词规律I\II Word Pattern
目录 290. 单词规律 Word Pattern 🌟 291. 单词规律 II Word Pattern ii 🌟🌟 🌟 每日一练刷题专栏 🌟 Rust每日一练 专栏 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 …...
linux_centos7.9/ubuntu20.04_下载镜像及百度网盘分享链接
1、镜像下载站点 网易开源镜像:http://mirrors.163.com/ 搜狐开源镜像:http://mirrors.sohu.com/ 阿里开源镜像:https://developer.aliyun.com/mirror/ 首都在线科技股份有限公司:http://mirrors.yun-idc.com/ 常州贝特康姆软件技…...
Reqable HTTP一站式开发+调试工具(小黄鸟作者另一力作、小黄鸟完美替代品)
本文所有教程及源码、软件仅为技术研究。不涉及计算机信息系统功能的删除、修改、增加、干扰,更不会影响计算机信息系统的正常运行。不得将代码用于非法用途,如侵立删!Reqable HTTP一站式开发+调试工具(小黄鸟作者另一力作、小黄鸟替代品) 环境 win10pixel4Android13概览 …...

Yacc 与 Lex 快速入门
Yacc 与 Lex 快速入门 简介: Lex 和 Yacc 是 UNIX 两个非常重要的、功能强大的工具。事实上, 如果你熟练掌握 Lex 和 Yacc 的话,它们的强大功能使创建 FORTRAN 和 C 的编译器如同儿戏。本文详细的讨论了编写自己的语言和编译器所 用到的这两…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
