平面电磁波的反射与折射,极化滤波作用
目录
引言
反射定律和折射定律
反射系数和折射系数
平面电磁波在理想介质分界面上的全反射和全折射
全反射
全折射
极化滤波作用
平面电磁波在良导体上的反射与折射
引言
再复杂的电磁波我们都可以看作是很多平面电磁波的叠加
我们在前面介绍的时候,我们认为传播的空间是无限大的
我们的水流如果在流动的过程中,我们会看到流体的流动会发生一些变化,我们在流体里面,把木头棒称作障碍物,两种介质的分界面,我们也可以理解为障碍物
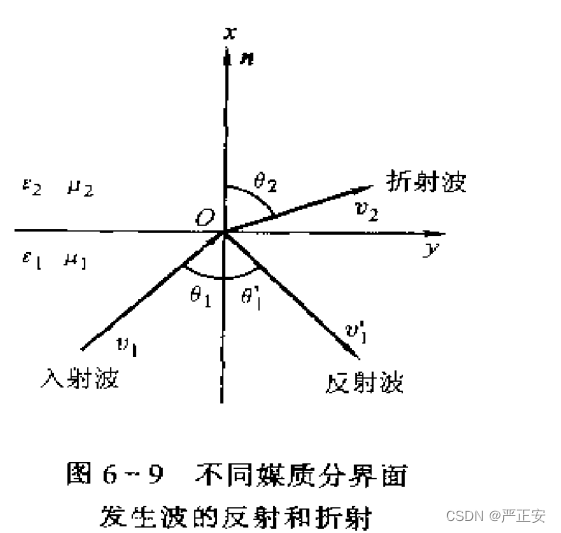
我们假设分片均匀,在穿过的时候,磁导率发生了突变,在外电场的作用下,会发生极化,在表面上会出现一层面极化电荷,这些电荷他要产生电场,如果是时变电磁波的作用下,媒质会产生磁化,会出现面磁化电流,也会产生随着时间变化的电磁场
我们媒质的分界面就是障碍物,媒质特性发生突变的地方就是障碍物
实际上飞机就是一个障碍物
但是我们知道,障碍物表面的形状可能很复杂,我们研究在分界面两侧,折射波和反射波的关系
入射波与法线的夹角为
折射波与法线的夹角为
现在我们知道了入射波的电场强度
我们要确定的是反射波传播的方向和法线的夹角
折射波传播的方向和法线的夹角
反射定律和折射定律
电磁场里面所谓的衔接条件,电场强度的切向分量要连续,在分界面上假设没有面传导电流
磁化以后,会产生面磁化电流,但并不影响
我们得到
依次可以推出
我们再看,由于入射波,反射波都在媒质1中前进
所以
由此我们得到
所以我们得到
我们得到
我们把这个定律称为折射定律(这就是所谓的斯奈尔定律)
由于我们的波碰到了介质分界面,透过分界面前进的时候,产生改变
如果是非磁性媒质
这就是我们的斯奈尔定律

反射系数和折射系数
这是我们两种媒质的分界面
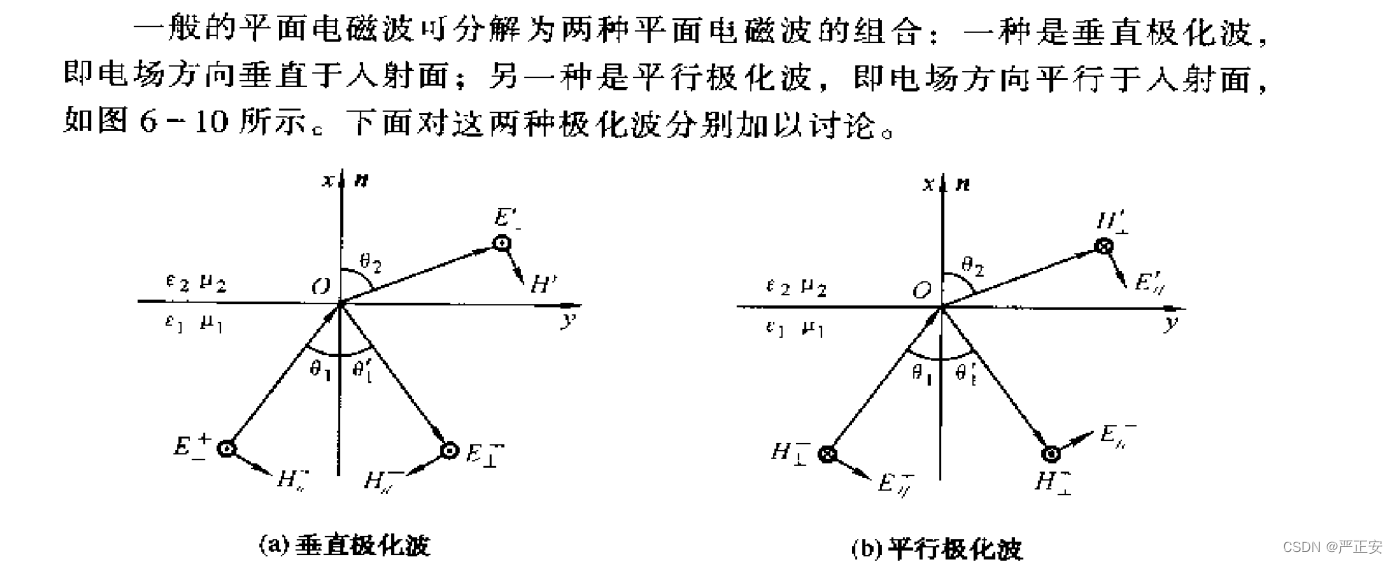
我们可以把一般的平面电磁波看作是两种平面电磁波的组合,一种是垂直极化波,即电场方向垂直于入射面,另一种是平行极化波,即电场方向平行于入射面
我们假设
在我们的媒质分界面上如果没有面传导电流
入射波和分界面相切,我们看到这时候
我们磁场强度的切向分量要连续
磁场强度的切向分量
我们称之为反射系数
我们还可以得到
这是分界面上的折射系数
同理我们可以得到
我们把这个称为菲涅尔公式
平面电磁波在理想介质分界面上的全反射和全折射
全反射
或者
如果应取
这个时候两个反射系数等于1
我们可以推出
这个时候就发生了全反射
当称为临界角,如果两边都是非磁性介质
我们可以得到
此时,从光密介质,射向光疏介质
这就是一种典型的表面波
我们把介质的分界面,也可以看作表面波导
如果我们在传输电磁波的时候,可以人为设置分界面,让电磁波沿着界面传播
光纤就是利用的就是这个原理,实际上是一种光波导,如果我们现在有一个介质棒
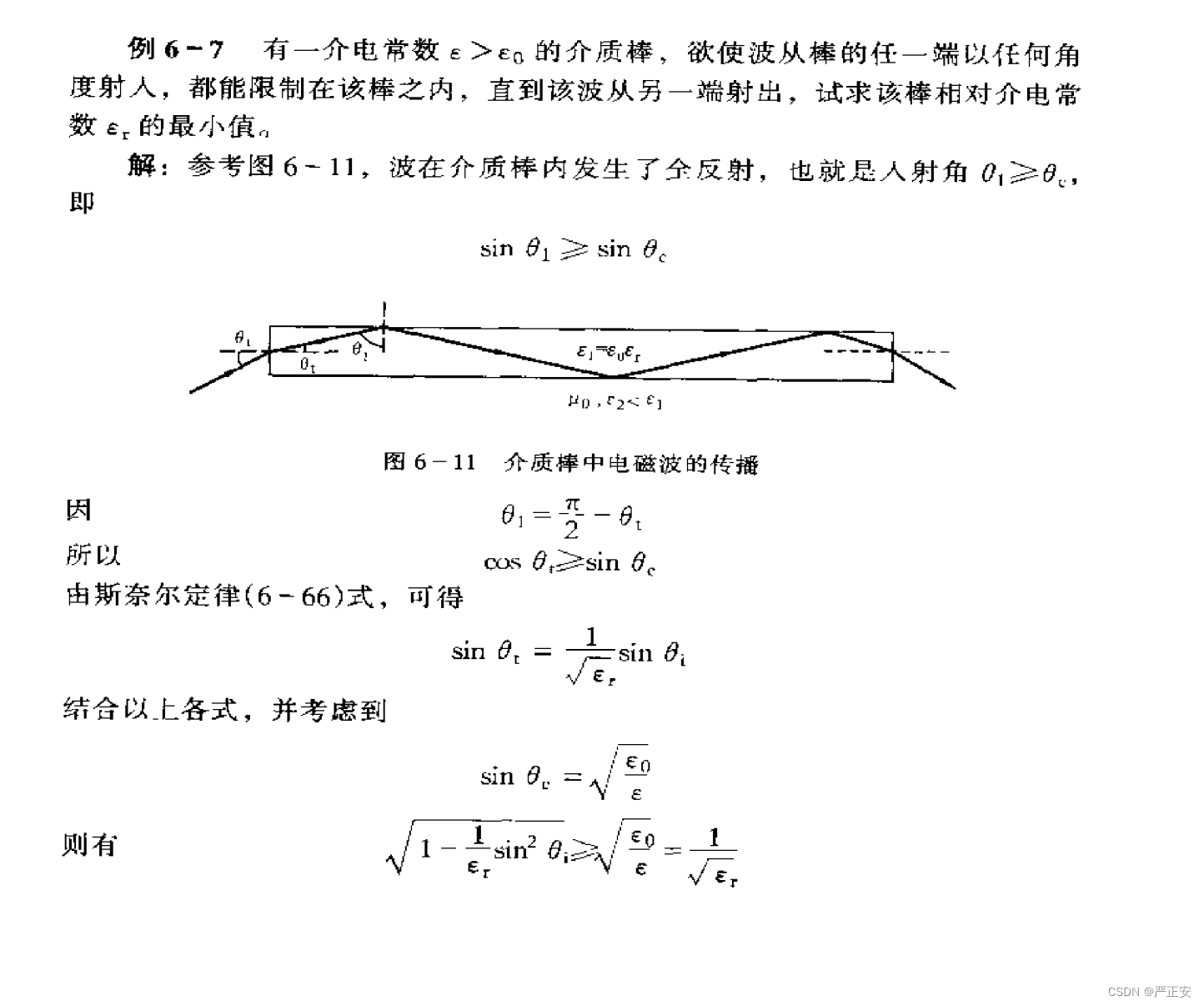

全折射
对于非磁性媒质来说
现在我们根据斯奈尔定律
代入我们可以得到
换句话说,两种非磁性的媒质

对于垂直极化波,在非磁性媒质中,不可能发生全折射
入射角不管怎么样调整,或多或少,在媒质里面都有反射波
调整了一个角度以后,会小一些,但是绝对消除不了
我们再看平行极化波
我们说如果要让
我们应该要让
对于非磁性媒质,我们得到
所以我们得到
现在这个公式也非常简单,我们把这个换成
我们解得
我们得到
极化滤波作用
我们一般把这个角度称作布鲁斯特角,也叫做起偏角
现在有一个电磁波既有垂直于平面的电场分量也有平行的电场分量
如果我们现在需要滤波,把垂直平面波和平行平面波分离开来
如果现在角度就是
平行极化波到这个分界面,全部折射到第二个介质里面
但是垂直极化波,或多或少就会有反射波,在反射波里面只有垂直极化波分量
这就起到了分离作用,这个称之为极化滤波作用
我们有时候把称为起偏角
平面电磁波在良导体上的反射与折射
如果现在我们有一个良导体


如果现在我们有一个良导体,它的电导率非常大,我们如果把良导体设想成一种理想介质
我们回想一下,在理想介质里面,传播常数是
良导体里面的波速是
我们得到
良导体里面电磁波都是垂直于分界面前进的
只要入射角不等于90度,我们再根据媒质2的波阻抗,我们近似可以得到
在良导体表面上,反射波的电场和入射波的电场在大小上近似相等,在相位上近似相反
相关文章:
平面电磁波的反射与折射,极化滤波作用
目录 引言 反射定律和折射定律 反射系数和折射系数 平面电磁波在理想介质分界面上的全反射和全折射 全反射 全折射 极化滤波作用 平面电磁波在良导体上的反射与折射 引言 再复杂的电磁波我们都可以看作是很多平面电磁波的叠加 我们在前面介绍的时候,我们认…...

键盘当鼠标用
当鼠标坏掉又需要使用电脑时发现触控板也不能用这就很烦那么键盘当鼠标用教程来了 使用键盘当鼠标的步骤如下: 1. 按住“AltShiftNum Lock”快捷键,弹出鼠标键开启咨询框,点击“是”按钮。 小键盘的数字就是方向/和*就是左右键切换5是单击 …...

动态规划part9 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
文章目录 198.打家劫舍思路思路代码官方题解代码 213.打家劫舍II思路思路代码官方代码困难 337.打家劫舍III思路思路代码官方题解代码困难 今日收获 198.打家劫舍 198.打家劫舍 思路 dp含义,偷前i个房,切第i个房偷 dp[i]max(dp[i-2],dp[i-3])nums[i] …...
【k8s系列】一分钟搭建MicroK8s Dashboard
本文基于上一篇文章的内容进行Dashboard搭建,如果没有看过上一篇的同学请先查阅上一篇文章 k8s系列】使用MicroK8s 5分钟搭建k8s集群含踩坑经验 使用MicroK8s搭建Dashboard很简单,只需要在Master节点按照以下几步操作 1.启用Dashboard插件 microk8s en…...
ArcEngine二次开发0——入门(下载 部署 组件学习)
折腾一下ArcGIS Engine二次开发。 目录 1、开发环境配置2、部署一个ArcGIS Engine应用程序3、ArcObject组件学习4、报错及解决4、其他 1、开发环境配置 参考:https://blog.csdn.net/H48662654/article/details/113384150 (使用ArcEngine前,…...
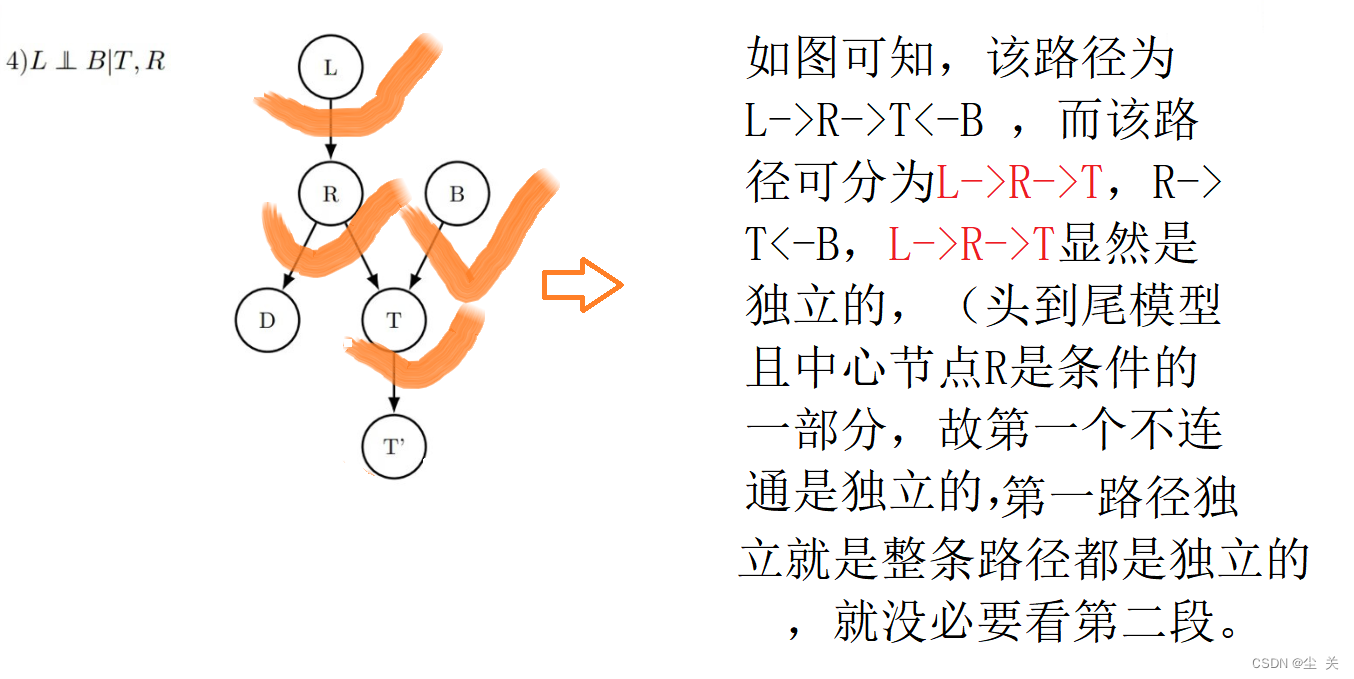
人工智能---D分离
D分离(D-Separation)是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点…...
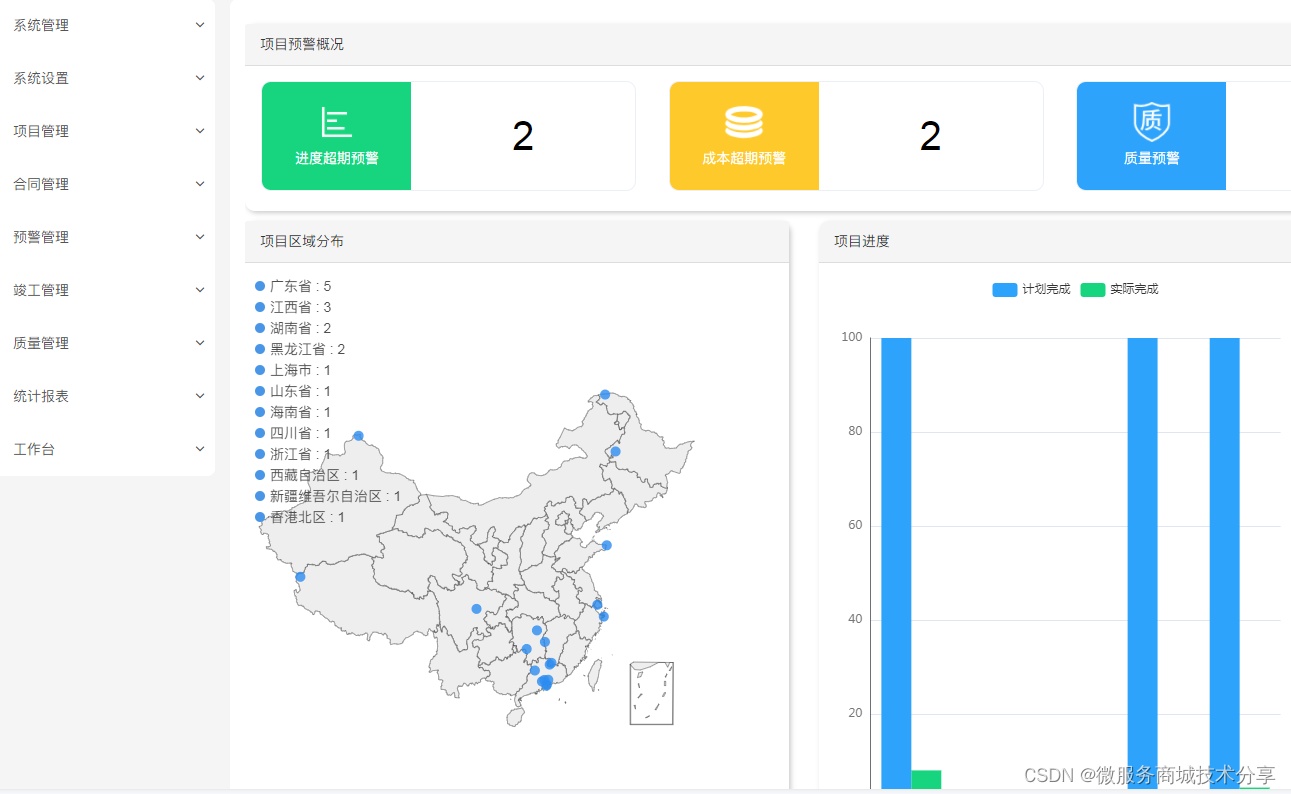
java spring cloud 企业工程项目管理系统源码-全面的工程项目管理
工程项目管理系统是指从事工程项目管理的企业(以下简称工程项目管理企业)受业主委托,按照合同约定,代表业主对工程项目的组织实施进行全过程或若干阶段的管理和服务。 如今建筑行业竞争激烈,内卷严重,…...

2023最新软件测试面试题【1000道题含答案】
1、自动化代码中,用到了哪些设计模式? 单例设计模式 工厂模式PO设计模式数据驱动模式面向接口编程设计模式 2、什么是断言( Assert) ? 断言Assert用于在代码中验证实际结果是不是符合预期结果,如果测试用例执行失败会抛出异常并提供断言日志 3、什么是web自动化测…...

【目标跟踪】MOT数据集GroundTruth可视化
MOT数据集格式简介 MOT15数据集下载:https://pan.baidu.com/s/1foGrBXvsanW8BI4eybqfWg?pwd8888 以下为一行gt示例: 1,1,1367,393,73,225,1,-1,-1,-1 各列数据对应含义如下 <frame>,<id>,<bb_left>,<bb_top>,<bb_width&g…...

软件测试的概念与过程----学习软件测试前的思考
软件测试的概念与过程----学习软件测试前的思考 1、软件测试工作是做什么的?2、那我做软件测试拿到一个软件产品我应该从哪里测试,怎末开始工作?3、测试早做好还是晚一些做好?4、软件测试能将软件测试的一点问题都没有嘛ÿ…...

Streamlit基础教程
streamlit是什么 streamlit是一个开源的python库,它能够快速的帮助我们创建定制化的web应用,而且还非常便于和他人分享,特别是在机器学习和数据科学领域。整个过程不需要你了解任何前端的知识,包括html、css、javascript等&#x…...

内网穿透技术
文章目录 前言1. 安装JAVA2. MCSManager安装3.局域网访问MCSM4.创建我的世界服务器5.局域网联机测试6.安装cpolar内网穿透7. 配置公网访问地址8.远程联机测试9. 配置固定远程联机端口地址9.1 保留一个固定tcp地址9.2 配置固定公网TCP地址9.3 使用固定公网地址远程联机 转载自内…...

计算机网络笔记:内部网关协议RIP
文章目录 1.协议RIP的工作原理2.距离向量算法3.坏消息传播得慢 1.协议RIP的工作原理 RIP的地位:RIP是内部网关协议IGP中最先得到广泛使用的协议,其中文译名为路由信息协议。 RIP概述: RIP是一种分布式的基于距离向量的路由选择协议&#x…...
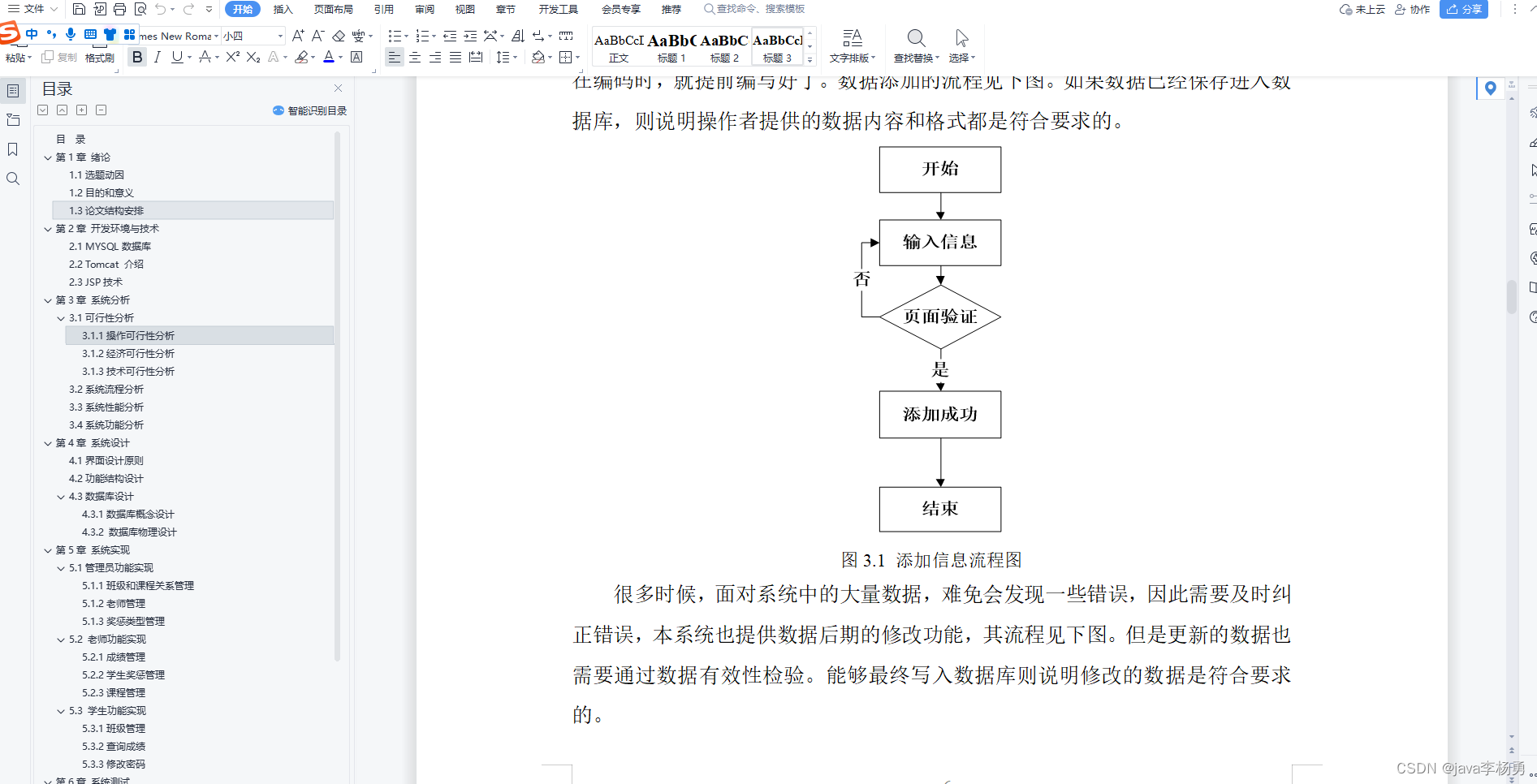
基于Java学生信息管理系统设计实现(源码+lw+部署文档+讲解等)
博主介绍: ✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精…...

PHP简单入门
PHP是一种流行的服务器端编程语言,被广泛用于Web开发。许多著名的网站和应用程序都是使用PHP编写的,例如Facebook、Wikipedia和WordPress等。本篇文章将为您介绍如何入门PHP编程。 环境配置 在开始使用PHP之前,需要先配置开发环境。要在本…...

java 客户端操作HDFS
1、windows上部署hadoop包 部署包win版本 源码包zip包 lib整合:共121个jar包 $HADOOP_PREFIX/share/hadoop/{common,hdfs,mapreduce,yarn,tools}/{lib,.}*.jar 将windows版本hadoop/bin/hadoop.dll 放到c:/windows/system32下 2、windows环境变量配置 hadoop的…...

区块链中的共识机制以及共识算法
目录 什么是共识 什么是共识机制 共识机制类型 1、基于工作证明(Proof of Work PoW)...

【计算机网络自顶向下】DNS简答题总结
主要功能:将域名解析为主机能识别的IP地址 DNS实现的功能 主机到IP地址的转换主机别名的转换邮件服务器别名负载均衡 DNS实现冗余服务器:一个IP地址集合对应同一个规范主机名 域名系统 分布式数据库:一个由多层DNS服务器实现的分布式数据库应…...

【QQ界面展示-实现自动回复 Objective-C语言】
一、刚才咱们监听键盘弹出事件,是怎么监听的, 1.监听键盘弹出事件的步骤 1)首先,在控制器的viewDidLoad方法中,创建一个NotificationCenter对象啊 2)通过center,让当前控制器的这个方法,监听这个通知, 3)然后,我们在这个通知里面,获取到键盘的Y值, 4)对我们的…...

-bash: ssh: command not found
解决方法: 命令安装SSH: yum -y install openssh-clients [roothad2 ~]# yum -y install openssh-clients Loaded plugins: fastestmirror Loading mirror speeds from cached hostfile * base: mirrors.qlu.edu.cn * extras: mirrors.ustc.edu.cn …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
