神经网络:激活函数
在计算机视觉中,激活函数是神经网络中的一种非线性函数,用于引入非线性变换和非线性特性到网络中。激活函数的作用、原理和意义如下:
1. 引入非线性变换:
神经网络的线性组合层(如卷积层和全连接层)只能表示线性关系,而计算机视觉任务通常涉及到复杂的非线性问题,如图像的边缘、纹理、形状等特征。激活函数通过对输入进行非线性变换,使网络能够学习和表示更加复杂的函数关系。
2. 增加网络的表达能力:
线性函数的组合仍然是线性函数,无法表示复杂的非线性关系。激活函数的引入扩展了网络的表达能力,使神经网络能够对输入数据进行非线性映射和特征提取,从而更好地捕捉和表示输入数据的复杂性。
3. 激活神经元:
激活函数的名称来源于它对神经元的激活过程。激活函数接收神经元的输入信号,通过非线性变换产生输出,从而决定神经元是否激活并传递信号给下一层。通过激活函数的作用,神经网络可以在不同层之间建立复杂的连接和信息传递。
4. 解决线性不可分问题:
计算机视觉中的很多任务,如图像分类、目标检测和图像分割,涉及到非线性的决策边界。激活函数的引入使得神经网络可以学习和表示这些非线性边界,从而提高了模型的分类性能和准确度。
从数学原理的角度来看,激活函数通过对输入进行非线性变换,引入非线性性质到神经网络中。这是因为线性函数的组合仍然是线性函数,无法表示复杂的非线性关系。激活函数通过增加非线性变换,使得神经网络能够学习和表示更加复杂的函数关系,提高模型的拟合能力和表达能力。
总之,激活函数在计算机视觉中的作用、原理和意义是通过引入非线性变换,增加网络的表达能力,激活神经元并解决线性不可分问题,使神经网络能够更好地适应和处理复杂的视觉任务。不同的激活函数具有不同的特性和优缺点,需要结合具体任务和网络结构进行选择和调整。
常见的激活函数包括:
1. Sigmoid函数:
- 公式:f(x) = 1 / (1 + exp(-x))
- 优点:输出值范围在(0, 1)之间,可以用作二分类问题的激活函数。
- 缺点:Sigmoid函数在输入较大或较小的情况下,梯度接近于0,导致梯度消失问题。
2. Tanh函数:
- 公式:f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
- 优点:输出值范围在(-1, 1)之间,相对于Sigmoid函数具有更大的动态范围。
- 缺点:仍然存在梯度消失问题。
3. ReLU函数(Rectified Linear Unit):
- 公式:f(x) = max(0, x)
- 优点:计算简单,能够在输入为正时保持梯度,有效解决梯度消失问题。
- 缺点:在输入为负时,梯度为0,导致神经元无法更新。
4. LeakyReLU函数:
- 公式:f(x) = max(ax, x),其中a为小于1的超参数
- 优点:在输入为负时引入了一个小的斜率,解决了ReLU函数的负值问题。
- 缺点:相对于ReLU函数计算略复杂。
5. ELU函数(Exponential Linear Unit):
- 公式: f(x) = x (if x > 0), f(x) = a * (exp(x) - 1) (if x <= 0,其中a为小于1的超参数)
- 优点:在输入为负时引入了一个负饱和度,解决了ReLU函数的负值问题。
- 缺点:计算较复杂。
下面是使用PyTorch绘制激活函数的图像和相应的代码示例:
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as npx = torch.linspace(-5, 5, 100)
y_sigmoid = torch.sigmoid(x)
y_tanh = torch.tanh(x)
y_relu = F.relu(x)
y_leaky_relu = F.leaky_relu(x, negative_slope=0.2)
y_elu = F.elu(x, alpha=1.0)plt.figure(figsize=(10, 6))
plt.plot(x.numpy(), y_sigmoid.numpy(), label='Sigmoid')
plt.plot(x.numpy(), y_tanh.numpy(), label='Tanh')
plt.plot(x.numpy(), y_relu.numpy(), label='ReLU')
plt.plot(x.numpy(), y_leaky_relu.numpy(), label='LeakyReLU')
plt.plot(x.numpy(), y_elu.numpy(), label='ELU')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Activation Functions')
plt.grid(True)
plt.show()
运行上述代码将绘制出激活函数的图像,可视化它们的形状和特点。请注意,PyTorch中的激活函数可以通过torch.nn.functional模块中的函数调用来实现。
下面是在PyTorch框架中使用这些激活函数的代码示例:
import torch
import torch.nn as nn# 创建一个带有激活函数的模型
class MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()self.fc = nn.Linear(10, 5) # 全连接层self.sigmoid = nn.Sigmoid() # Sigmoid激活函数self.tanh = nn.Tanh() # Tanh激活函数self.relu = nn.ReLU() # ReLU激活函数self.leaky_relu = nn.LeakyReLU(negative_slope=0.2) # LeakyReLU激活函数self.elu = nn.ELU(alpha=1.0) # ELU激活函数def forward(self, x):x = self.fc(x)x = self.sigmoid(x)x = self.tanh(x)x = self.relu(x)x = self.leaky_relu(x)x = self.elu(x)return x# 创建一个输入张量
input_tensor = torch.randn(1, 10)# 实例化模型并进行前向传播
model = MyModel()
output = model(input_tensor)print(output)
以上代码展示了如何在PyTorch中使用不同的激活函数。您可以根据实际需求选择适合的激活函数来构建您的模型。
相关文章:

神经网络:激活函数
在计算机视觉中,激活函数是神经网络中的一种非线性函数,用于引入非线性变换和非线性特性到网络中。激活函数的作用、原理和意义如下: 1. 引入非线性变换: 神经网络的线性组合层(如卷积层和全连接层)只能表…...
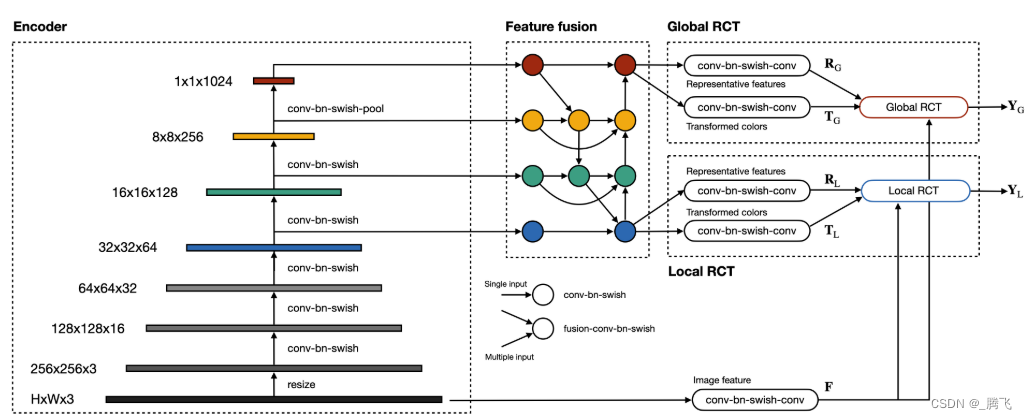
图像色彩增强相关论文阅读-Representative Color Transform for Image Enhancement(ICCV2021)
文章目录 Representative Color Transform for Image EnhancementAbstractIntroductionRelated workMethod实验Conclusion Representative Color Transform for Image Enhancement 作者:Hanul Kim1, Su-Min Choi2, Chang-Su Kim3, Yeong Jun Koh 单位:S…...
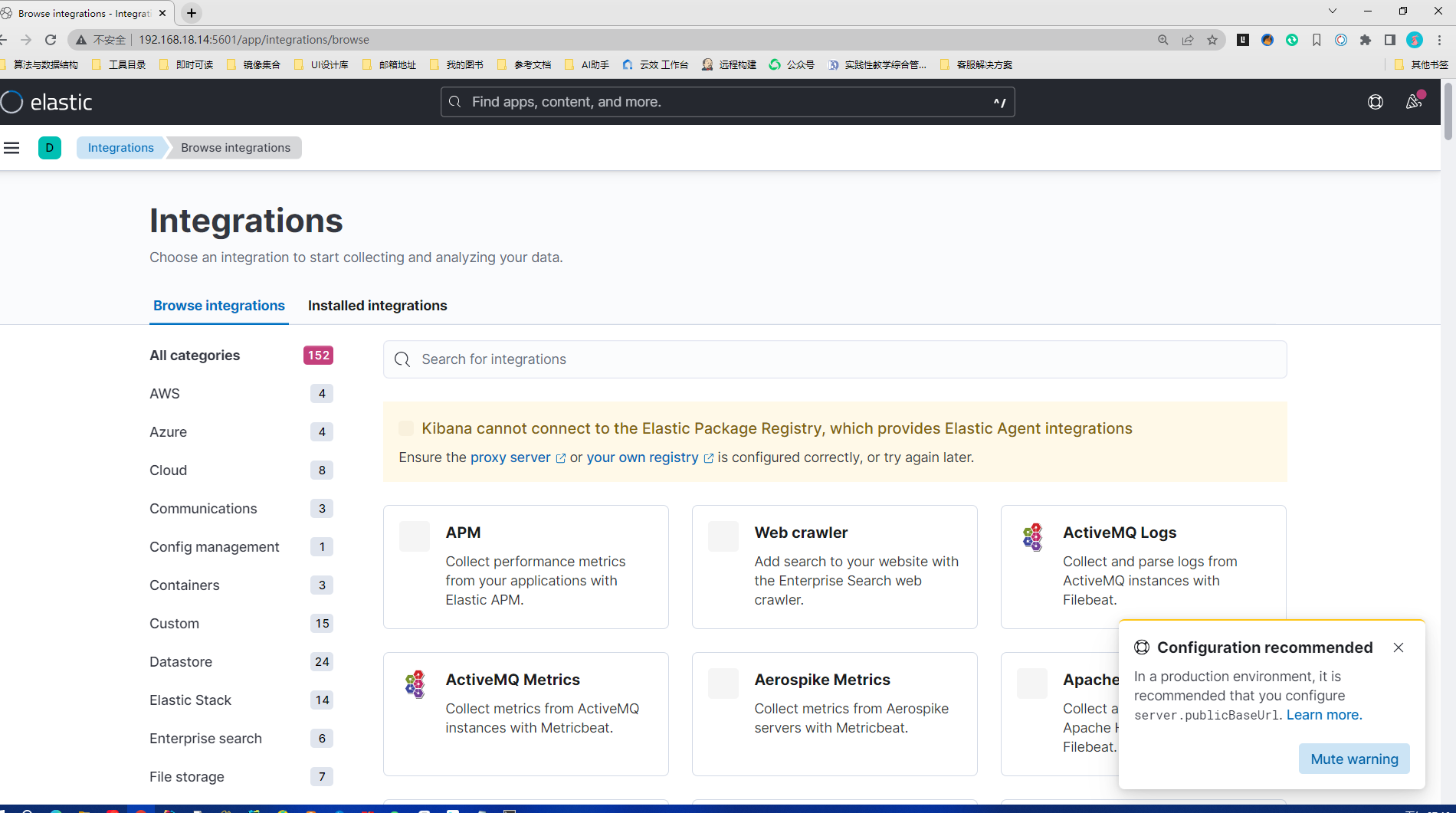
Elasticsearch介绍与应用
Elasticsearch介绍与应用 Elasticsearch的官方文档。 Elasticsearch官网参考文档:https://www.elastic.co/guide/index.html Elasticsearch官方下载地址:https://www.elastic.co/cn/downloads/elasticsearch mvnrepository依赖库地址:http…...

JavaEE规范
Servlet:用于开发 Web 应用程序的 API,定义了处理 HTTP 请求和响应的方式。JSP(JavaServer Pages):一种在服务器端生成动态网页的技术,允许将 Java 代码嵌入到 HTML 页面中。(注意JSP本质就是一个Servlet)J…...
)
嵌入式实时操作系统的设计与开发New(八)
创建线程 用户在基于RTOS开发应用程序前,首先要创建线程。 用户创建一个线程时须指定用户希望采用的调度策略。 例如,用户想创建一个周期性执行的线程: acoral_period_policy_data_t* data; data acoral_malloc(sizeof(acoral_period_poli…...

MySQL事务相关笔记
杂项 InnoDB最大特点:支持事务和行锁; MyISAM不支持事务 介绍 一个事务是由一条或者多条对数据库操作的SQL语句所组成的一个不可分割的单元,只有当事务中的所有操作都正常执行完了,整个事务才会被提交给数据库。事务有如下特性…...

如何利用AI高效率快速调色
在设计行业中,时间是非常宝贵的资源,而设计师们常常需要应对繁忙的工作日程和紧迫的截止日期。为了提高工作效率和节省时间,越来越多的设计师开始利用人工智能(AI)技术中的高效调色功能。本文将介绍如何利用AI高效率快…...
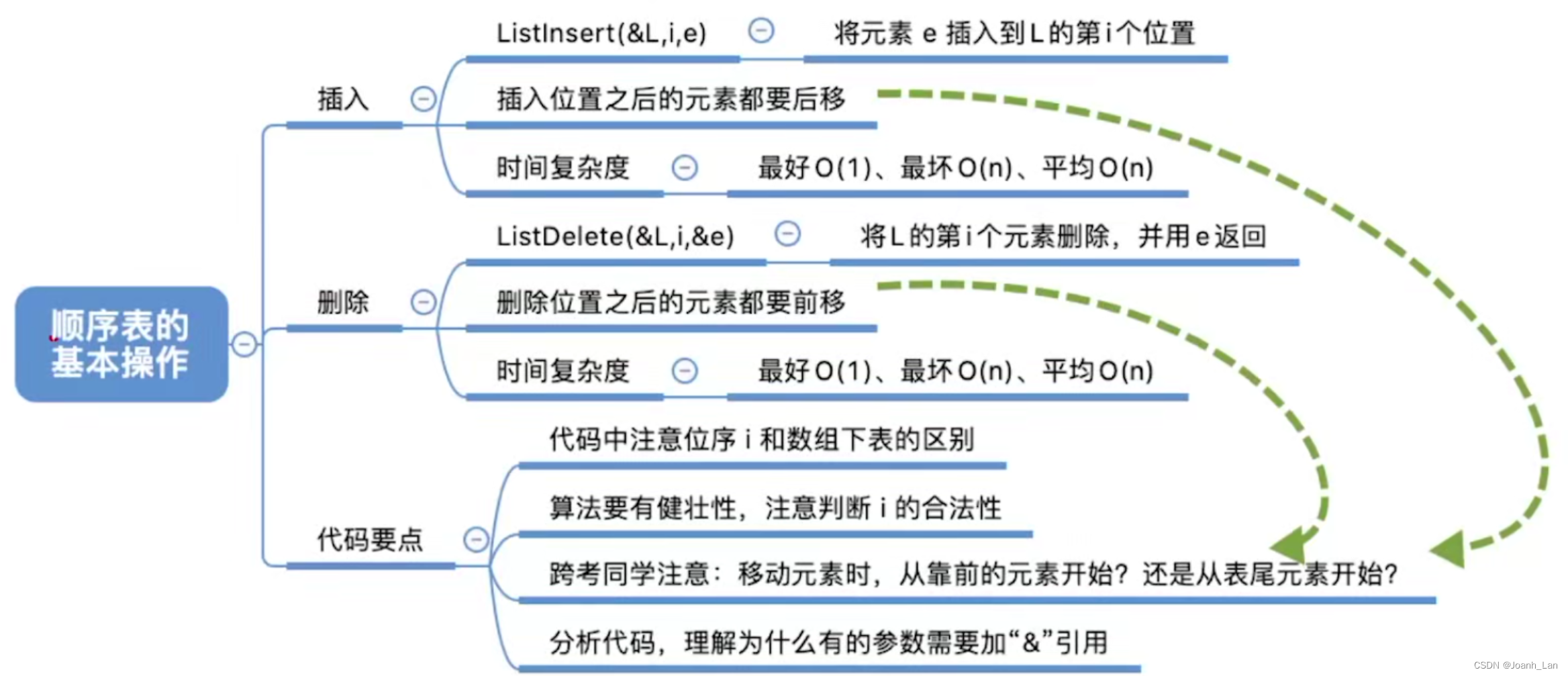
数据结构--顺序表的基本操作--插入 and 删除
数据结构–顺序表的基本操作–插入 顺序表的插入操作 实现目标 ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。 typedef struct {int data[MaxSize];int len; }Sqlist;代码实现: #include <stdio.h> #include <stdlib.h> …...

BCSP-玄子Java开发之Java Web编程CH01_初识动态网页
BCSP-玄子Java开发之Java Web编程CH01_初识动态网页 1.1 B/S架构 B/S架构:浏览器/服务器 程序完全部署在服务器上使用浏览器访问服务器无需单独安装客户端软件 为什么要使用B/S架构 B/S与C/S比较B/S架构C/S架构软件安装浏览器需要专门的客户端应用升级维护客户…...
【软件教程】农林生环、水文、海洋、水环境、大气科学、人工智能、碳中和、碳排放、3S、R与统计等软件模型
本文涉及领域水文水资源、大气科学、农林生态、地信遥感、统计分析、编程语言等... 从软件基础到实践案例应用操作,手把手教学,提供永久回放观看和助学群长期辅助指导。适合课题组人员一站式学习,科研人员技术提升、企业单位工程项目、高校论…...

如何加入开源社
开源社成立于 2014 年,是由志愿贡献于开源事业的个人成员,依 “贡献、共识、共治” 原则所组成,始终维持厂商中立、公益、非营利的特点,是最早以 “开源治理、国际接轨、社区发展、项目孵化” 为使命的开源社区联合体。开源社积极…...

软件开发中的破窗效应
应该有很多人已经知道破窗效应【注1】这个社会学 (犯罪学)的词语,破窗效应最先由社会学家James Q. Wilson和George L. Kelling在一篇名为《Broken Windows》的文章中提出【注2】: “一个房子如果窗户破了,没有人去修补…...

机器视觉初步6-1:基于梯度的图像分割
把基于梯度的图像分割单独拿出来。 文章目录 一、图像梯度相关算子的原理1. Sobel算子2. Prewitt算子3. Roberts算子 二、python和halcon算子实现1.python实现2.halcon实现 基于梯度的图像分割方法利用像素之间的梯度信息来进行图像分割。 梯度 1是图像中像素灰度值变化最快的…...

从0开始,精通Go语言Rest微服务架构和开发
说在前面 现在拿到offer超级难,甚至连面试电话,一个都搞不到。 尼恩的技术社区中(50),很多小伙伴凭借 “左手云原生右手大数据”的绝活,拿到了offer,并且是非常优质的offer,据说年…...

Sui x KuCoin Labs夏季黑客松|本周Workshop预告
自Sui x KuCoin Labs夏季黑客松推出以来已有四周的时间,期间收获了众多开发者的积极报名和热情参与。随着黑客松报名即将进入尾声,同期举办的Workshop也迎来了本周的最后一波。本周的黑客松Workshop邀请到MoveEX和Mirror World的负责人作为嘉宾为大家带…...

从电源 LED 读取智能手机的秘密?
研究人员设计了一种新的攻击方法,通过记录读卡器或智能手机打开时的电源 LED,使用 iPhone 摄像头或商业监控系统恢复存储在智能卡和智能手机中的加密密钥。 众所周知,这是一种侧信道攻击。 通过密切监视功耗、声音、电磁辐射或执行操作所需…...
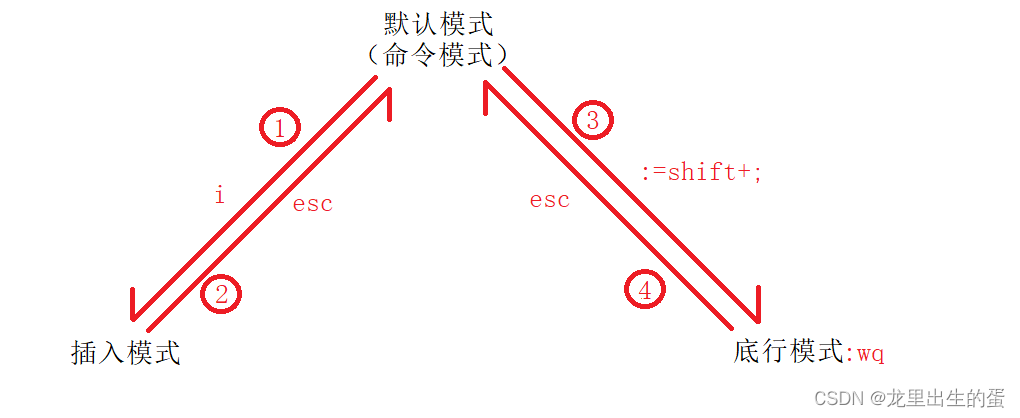
【Linux编辑器-vim使用】
目录 Linux编辑器-vim使用1.vim的基本概念2.vim的基本操作3.vim正常模式命令集4.vim末行模式命令集 Linux编辑器-vim使用 1.vim的基本概念 目前了解的vim有三种模式(其实有好多模式),分别是命令模式、插入模式和底行模式,各模式…...
安装Apache mysql php
目录 一.Apache网站服务 Apache——》静态页面处理——》将静态处理交给PHP Apache简介 安装Apache服务 编辑 安装软件思路 二.安装mysql数据库 1. 安装依赖包 2.创建程序用户管理 3.加压安装包 这边就安装完成了编辑 重点来了 报错了 没有空间 我最后的解决 方法…...
【人工智能】— 神经网络、前向传播、反向传播、梯度下降、局部最小值、多层前馈网络、缓解过拟合的策略
【人工智能】— 神经网络、前向传播、反向传播 前向传播反向传播梯度下降局部最小值多层前馈网络表示能力多层前馈网络局限缓解过拟合的策略 前向传播和反向传播都是神经网络训练中常用的重要算法。 前向传播是指将输入数据从输入层开始经过一系列的权重矩阵和激活函数的计算后…...
小文智能自定义变量详解
在小文交互场景设计时,有一个特殊功能,叫做自定义变量。有时,根据外呼对象的不同,需要对用户传达不同的内容,比如称呼、地址、公司名称等等。此时,就可以使用小文交互的自定义变量功能来实现对不同用户呼出…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
