数据结构--顺序表的基本操作--插入 and 删除
数据结构–顺序表的基本操作–插入
顺序表的插入操作
实现目标
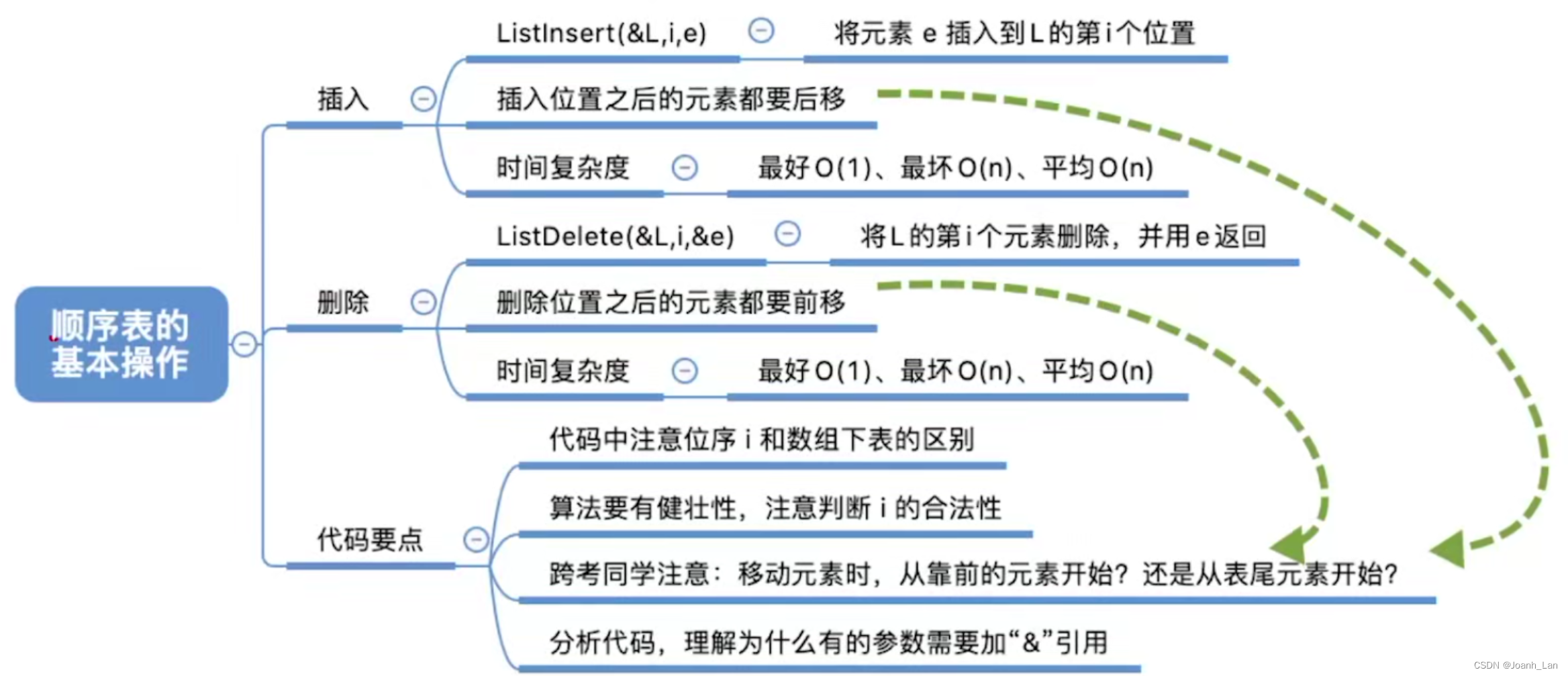
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
typedef struct
{int data[MaxSize];int len;
}Sqlist;


代码实现:
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10 //定于的最大长度typedef struct
{int data[MaxSize];int len;
}Sqlist;
void InitList(Sqlist &L)
{L.len = 0;
}
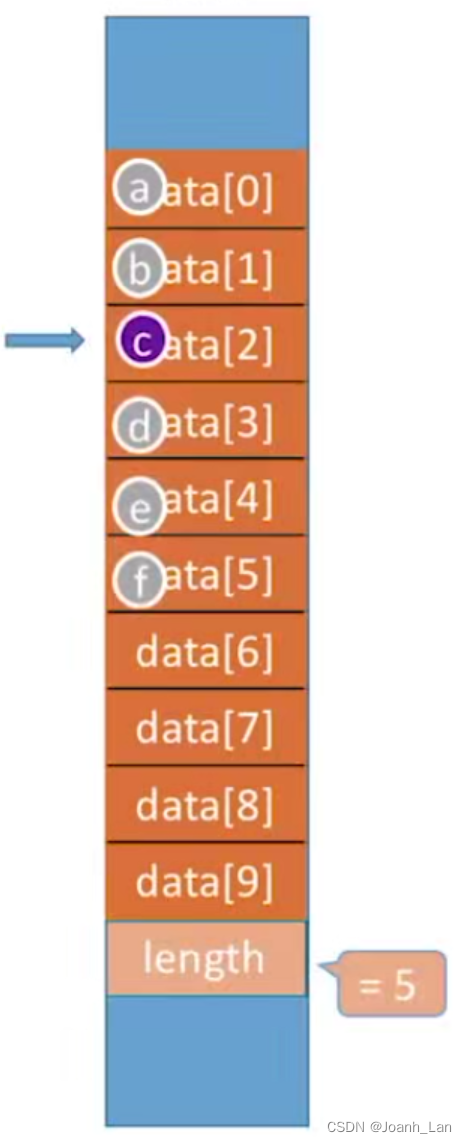
bool ListInsert(Sqlist &L, int idx, int e)
{if (idx > L.len + 1 || idx < 1) //判断是否合法return false;if (L.len >= MaxSize)return false;for (int j = L.len; j >= idx; j--) //将第idx个元素及之后的元素后移L.data[j] = L.data[j - 1]; L.data[idx - 1] = e; //在位置i处放入eL.len++; //长度加1return true;
}
int main()
{Sqlist L;InitList(L);if (ListInsert(L, 1, 1))printf("Inserted successfully\n");if (ListInsert(L, 2, 2))printf("Inserted successfully\n");// 测试结果for (int i = 0; i < L.len; i++)printf("%d ", L.data[i]);
}
ps:
好的算法,应该具有“健壮性”能处理异常情况,并给使用者反馈。
时间复杂度
最好情况:新元素插入到表尾,不需要移动元素 idx = n+1,循环0次;
最好时间复杂度 \color{red}最好时间复杂度 最好时间复杂度=O(1)
最坏情况:新元素插入到表头,需要将原有的n个元素全都向后移动 idx= 1,循环n次;
最坏时间复杂度 \color{red}最坏时间复杂度 最坏时间复杂度= O(n);
平均情况:假设新元素插入到任何一个位置的概率相同,即idx= 1,2,3, … len+1的概率都是 p = 1 n + 1 p=\frac{1}{n+1} p=n+11 idx = 1,循环n次;idx=2时,循环n-1次; idx=3,循环n-2次…idx=n+1时,循环0次
平均循环次数 = n p + ( n − 1 ) p + ( n − 2 ) p + . . . + 1 p = n ( n + 1 ) 2 × 1 n + 1 = n 2 np + (n-1)p + (n-2)p + ... + 1p = \frac{n(n + 1)}{2} \times \frac{1}{n + 1} = \frac{n}{2} np+(n−1)p+(n−2)p+...+1p=2n(n+1)×n+11=2n
平均时间复杂度 \color{red}{平均时间复杂度} 平均时间复杂度 = O(n)
顺序表的删除操作
实现目标
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值。


代码实现
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10 //定于的最大长度typedef struct
{int data[MaxSize];int len;
}Sqlist;
void InitList(Sqlist &L)
{L.len = 0;
}
bool ListInsert(Sqlist &L, int idx, int e)
{if (idx > L.len + 1 || idx < 1) //判断是否合法return false;if (L.len >= MaxSize)return false;for (int j = L.len; j >= idx; j--) //将第idx个元素及之后的元素后移L.data[j] = L.data[j - 1]; L.data[idx - 1] = e; //在位置i处放入eL.len++; //长度加1return true;
}
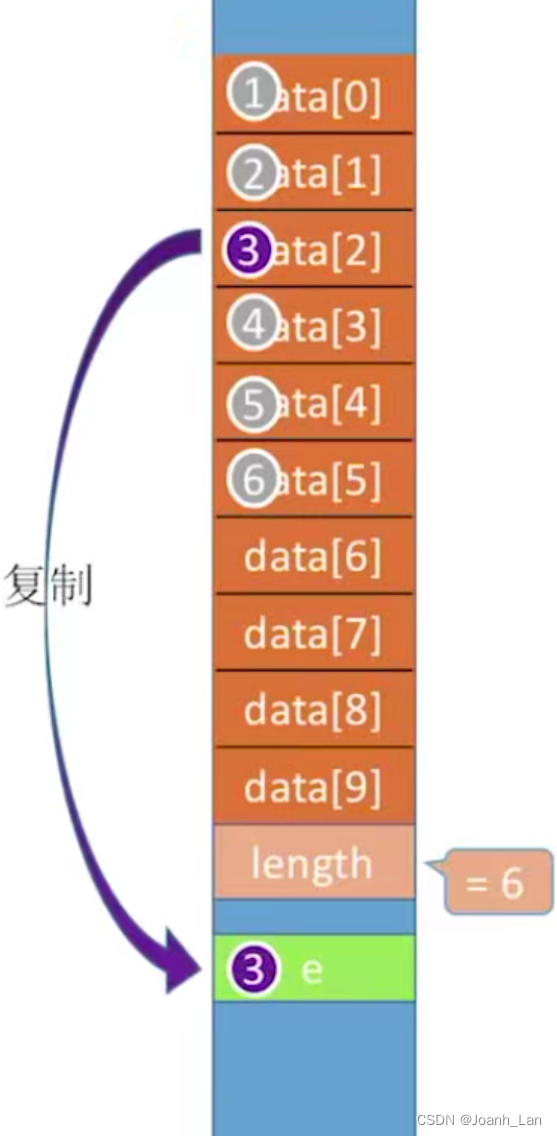
bool ListDelete(Sqlist &L, int idx, int &e)
{if (idx > L.len && idx < 1) //判断i的范围是否有效return false;e = L.data[idx - 1]; //将被删除的元素赋值给efor (int j = idx - 1; j < L.len; j++) //将第i个位置后的元素前移L.data[j] = L.data[j + 1];L.len--; //线性表长度减1return true;
}
int main()
{Sqlist L;InitList(L);if (ListInsert(L, 1, 1))printf("Inserted successfully\n");if (ListInsert(L, 2, 2))printf("Inserted successfully\n");int e = -1;if (ListDelete(L,1,e))printf("Deleted successfully\n");// 测试结果for (int i = 0; i < L.len; i++)printf("%d ", L.data[i]);
}
时间复杂度
最好情况:删除表尾元素,不需要移动其他元素 idx= n 循环0次;
最好时间复杂度 \color{red}最好时间复杂度 最好时间复杂度=O(1)
最坏情况:删除表头元素,需要将后续的n-1个元素全都向前移动 idx= 1,循环 n-1 次;
最坏时间复杂度 \color{red}最坏时间复杂度 最坏时间复杂度= O(n);
平均情况:假设删除任何一个元素的概率相同,即 idx= 1,2,3. … , len的概率都是 p = 1 n p=\frac{1}{n} p=n1
idx = 1,循环 n-1 次; idx=2 时,循环n-2次; idx=3,循环n-3 次… idx = n 时,循环 0 次
平均循环次数 = ( n − 1 ) p + ( n − 2 ) p + . . . . . . + 1 p = n ( n − 1 ) 2 × 1 n = n − 1 2 (n-1)p+(n-2)p+......+1p = \frac{n(n-1)}{2} \times \frac{1}{n} = \frac{n-1}{2} (n−1)p+(n−2)p+......+1p=2n(n−1)×n1=2n−1
平均时间复杂度 \color{red}平均时间复杂度 平均时间复杂度 = O(n)
知识点回顾与重要考点
相关文章:

数据结构--顺序表的基本操作--插入 and 删除
数据结构–顺序表的基本操作–插入 顺序表的插入操作 实现目标 ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。 typedef struct {int data[MaxSize];int len; }Sqlist;代码实现: #include <stdio.h> #include <stdlib.h> …...

BCSP-玄子Java开发之Java Web编程CH01_初识动态网页
BCSP-玄子Java开发之Java Web编程CH01_初识动态网页 1.1 B/S架构 B/S架构:浏览器/服务器 程序完全部署在服务器上使用浏览器访问服务器无需单独安装客户端软件 为什么要使用B/S架构 B/S与C/S比较B/S架构C/S架构软件安装浏览器需要专门的客户端应用升级维护客户…...
【软件教程】农林生环、水文、海洋、水环境、大气科学、人工智能、碳中和、碳排放、3S、R与统计等软件模型
本文涉及领域水文水资源、大气科学、农林生态、地信遥感、统计分析、编程语言等... 从软件基础到实践案例应用操作,手把手教学,提供永久回放观看和助学群长期辅助指导。适合课题组人员一站式学习,科研人员技术提升、企业单位工程项目、高校论…...

如何加入开源社
开源社成立于 2014 年,是由志愿贡献于开源事业的个人成员,依 “贡献、共识、共治” 原则所组成,始终维持厂商中立、公益、非营利的特点,是最早以 “开源治理、国际接轨、社区发展、项目孵化” 为使命的开源社区联合体。开源社积极…...

软件开发中的破窗效应
应该有很多人已经知道破窗效应【注1】这个社会学 (犯罪学)的词语,破窗效应最先由社会学家James Q. Wilson和George L. Kelling在一篇名为《Broken Windows》的文章中提出【注2】: “一个房子如果窗户破了,没有人去修补…...

机器视觉初步6-1:基于梯度的图像分割
把基于梯度的图像分割单独拿出来。 文章目录 一、图像梯度相关算子的原理1. Sobel算子2. Prewitt算子3. Roberts算子 二、python和halcon算子实现1.python实现2.halcon实现 基于梯度的图像分割方法利用像素之间的梯度信息来进行图像分割。 梯度 1是图像中像素灰度值变化最快的…...

从0开始,精通Go语言Rest微服务架构和开发
说在前面 现在拿到offer超级难,甚至连面试电话,一个都搞不到。 尼恩的技术社区中(50),很多小伙伴凭借 “左手云原生右手大数据”的绝活,拿到了offer,并且是非常优质的offer,据说年…...

Sui x KuCoin Labs夏季黑客松|本周Workshop预告
自Sui x KuCoin Labs夏季黑客松推出以来已有四周的时间,期间收获了众多开发者的积极报名和热情参与。随着黑客松报名即将进入尾声,同期举办的Workshop也迎来了本周的最后一波。本周的黑客松Workshop邀请到MoveEX和Mirror World的负责人作为嘉宾为大家带…...

从电源 LED 读取智能手机的秘密?
研究人员设计了一种新的攻击方法,通过记录读卡器或智能手机打开时的电源 LED,使用 iPhone 摄像头或商业监控系统恢复存储在智能卡和智能手机中的加密密钥。 众所周知,这是一种侧信道攻击。 通过密切监视功耗、声音、电磁辐射或执行操作所需…...
【Linux编辑器-vim使用】
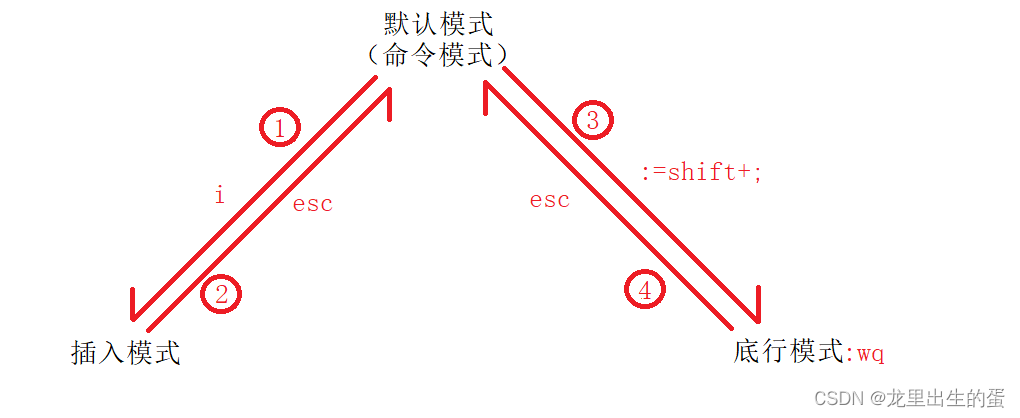
目录 Linux编辑器-vim使用1.vim的基本概念2.vim的基本操作3.vim正常模式命令集4.vim末行模式命令集 Linux编辑器-vim使用 1.vim的基本概念 目前了解的vim有三种模式(其实有好多模式),分别是命令模式、插入模式和底行模式,各模式…...
安装Apache mysql php
目录 一.Apache网站服务 Apache——》静态页面处理——》将静态处理交给PHP Apache简介 安装Apache服务 编辑 安装软件思路 二.安装mysql数据库 1. 安装依赖包 2.创建程序用户管理 3.加压安装包 这边就安装完成了编辑 重点来了 报错了 没有空间 我最后的解决 方法…...
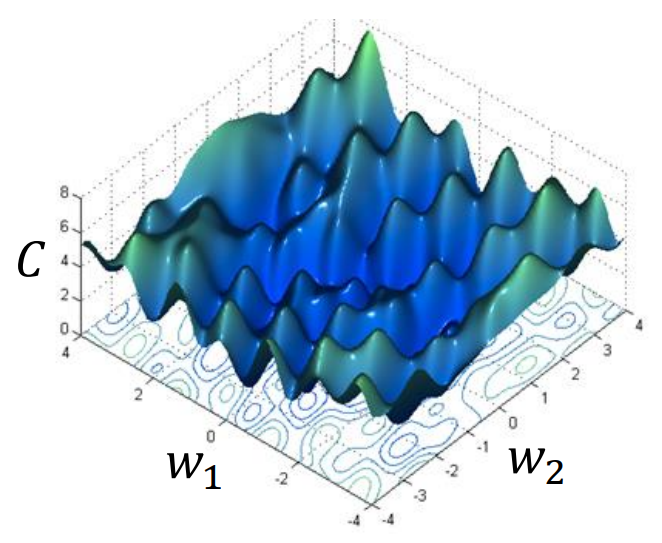
【人工智能】— 神经网络、前向传播、反向传播、梯度下降、局部最小值、多层前馈网络、缓解过拟合的策略
【人工智能】— 神经网络、前向传播、反向传播 前向传播反向传播梯度下降局部最小值多层前馈网络表示能力多层前馈网络局限缓解过拟合的策略 前向传播和反向传播都是神经网络训练中常用的重要算法。 前向传播是指将输入数据从输入层开始经过一系列的权重矩阵和激活函数的计算后…...
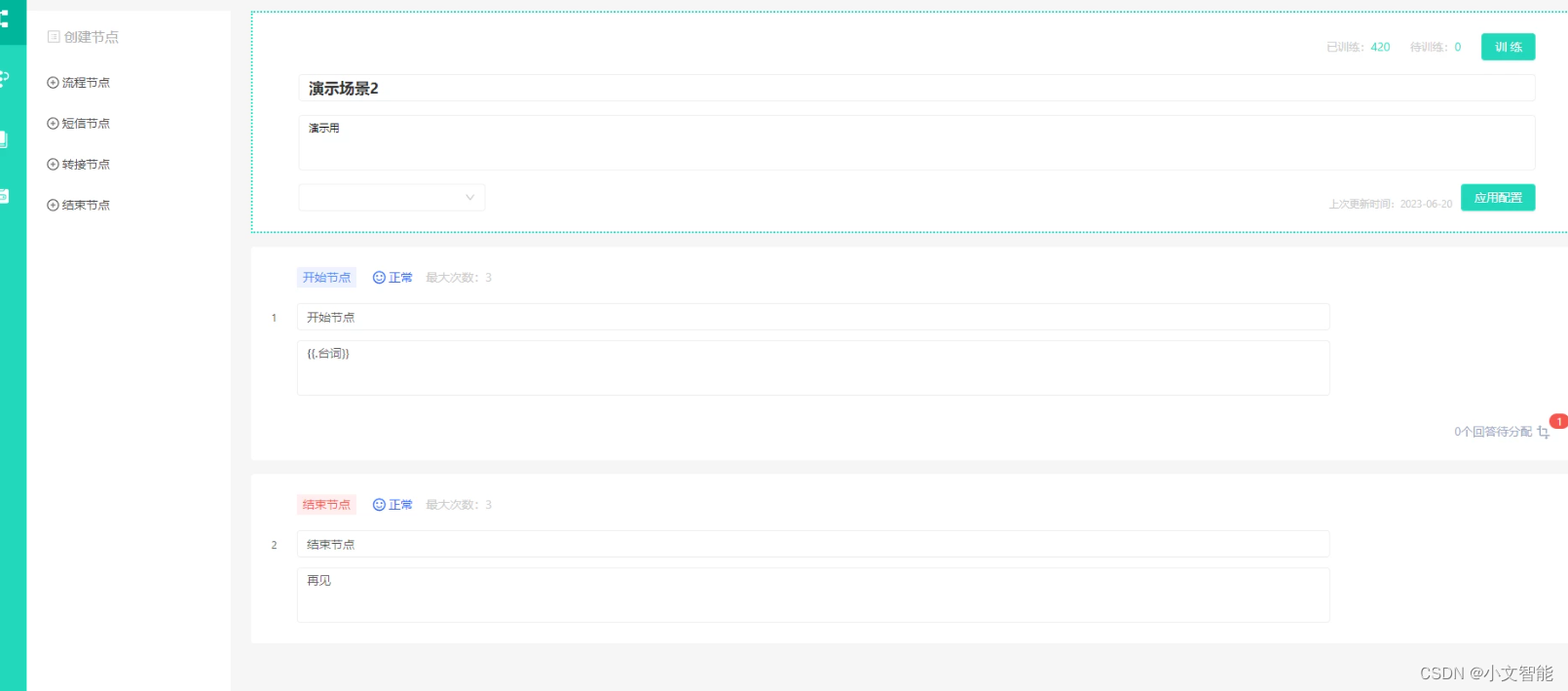
小文智能自定义变量详解
在小文交互场景设计时,有一个特殊功能,叫做自定义变量。有时,根据外呼对象的不同,需要对用户传达不同的内容,比如称呼、地址、公司名称等等。此时,就可以使用小文交互的自定义变量功能来实现对不同用户呼出…...
平面电磁波的反射与折射,极化滤波作用
目录 引言 反射定律和折射定律 反射系数和折射系数 平面电磁波在理想介质分界面上的全反射和全折射 全反射 全折射 极化滤波作用 平面电磁波在良导体上的反射与折射 引言 再复杂的电磁波我们都可以看作是很多平面电磁波的叠加 我们在前面介绍的时候,我们认…...

键盘当鼠标用
当鼠标坏掉又需要使用电脑时发现触控板也不能用这就很烦那么键盘当鼠标用教程来了 使用键盘当鼠标的步骤如下: 1. 按住“AltShiftNum Lock”快捷键,弹出鼠标键开启咨询框,点击“是”按钮。 小键盘的数字就是方向/和*就是左右键切换5是单击 …...

动态规划part9 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
文章目录 198.打家劫舍思路思路代码官方题解代码 213.打家劫舍II思路思路代码官方代码困难 337.打家劫舍III思路思路代码官方题解代码困难 今日收获 198.打家劫舍 198.打家劫舍 思路 dp含义,偷前i个房,切第i个房偷 dp[i]max(dp[i-2],dp[i-3])nums[i] …...
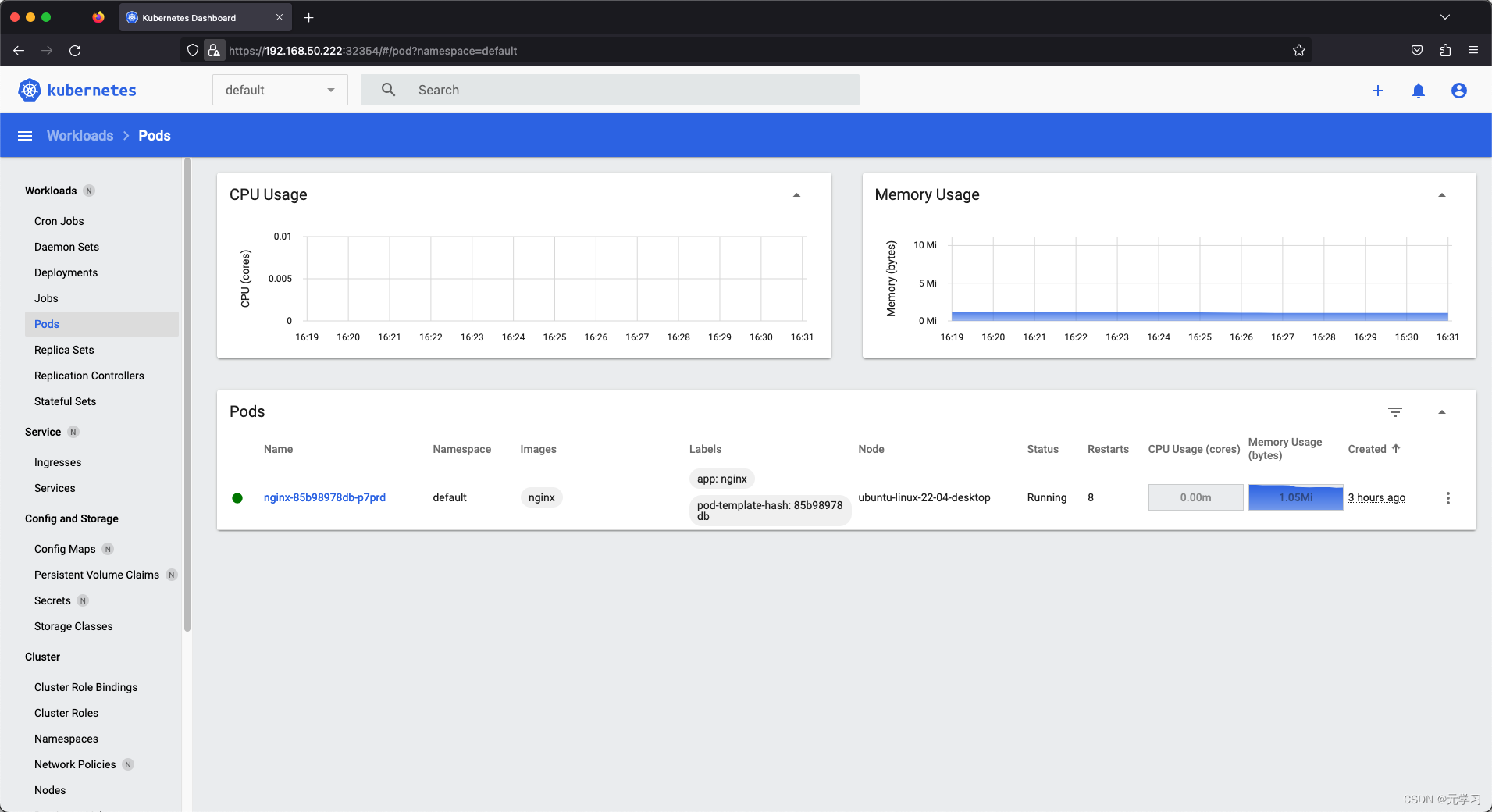
【k8s系列】一分钟搭建MicroK8s Dashboard
本文基于上一篇文章的内容进行Dashboard搭建,如果没有看过上一篇的同学请先查阅上一篇文章 k8s系列】使用MicroK8s 5分钟搭建k8s集群含踩坑经验 使用MicroK8s搭建Dashboard很简单,只需要在Master节点按照以下几步操作 1.启用Dashboard插件 microk8s en…...
ArcEngine二次开发0——入门(下载 部署 组件学习)
折腾一下ArcGIS Engine二次开发。 目录 1、开发环境配置2、部署一个ArcGIS Engine应用程序3、ArcObject组件学习4、报错及解决4、其他 1、开发环境配置 参考:https://blog.csdn.net/H48662654/article/details/113384150 (使用ArcEngine前,…...
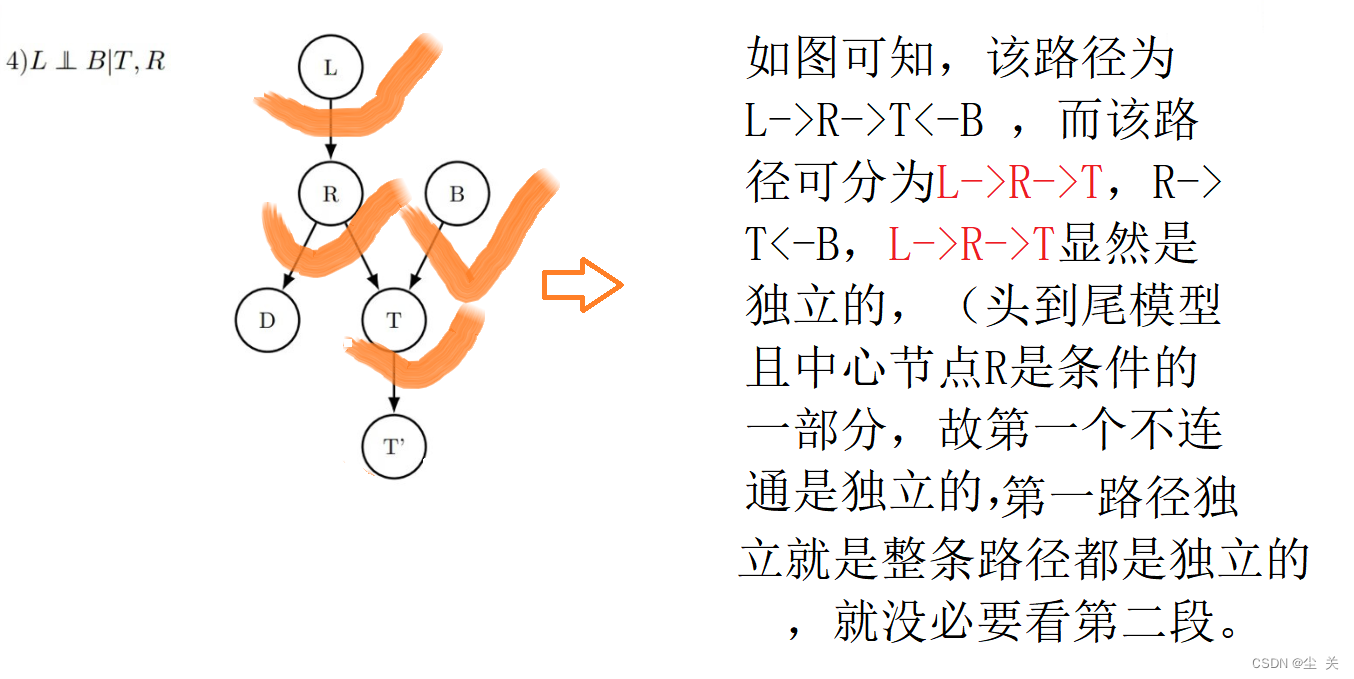
人工智能---D分离
D分离(D-Separation)是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点…...
java spring cloud 企业工程项目管理系统源码-全面的工程项目管理
工程项目管理系统是指从事工程项目管理的企业(以下简称工程项目管理企业)受业主委托,按照合同约定,代表业主对工程项目的组织实施进行全过程或若干阶段的管理和服务。 如今建筑行业竞争激烈,内卷严重,…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
