【人工智能】— 神经网络、前向传播、反向传播、梯度下降、局部最小值、多层前馈网络、缓解过拟合的策略
【人工智能】— 神经网络、前向传播、反向传播
- 前向传播
- 反向传播
- 梯度下降
- 局部最小值
- 多层前馈网络表示能力
- 多层前馈网络局限
- 缓解过拟合的策略
前向传播和反向传播都是神经网络训练中常用的重要算法。
前向传播是指将输入数据从输入层开始经过一系列的权重矩阵和激活函数的计算后,最终得到输出结果的过程。在前向传播中,神经网络会将每一层的输出作为下一层的输入,直到输出层得到最终的结果。
反向传播是指在神经网络训练过程中,通过计算损失函数的梯度,将梯度从输出层开始逆向传播到输入层,以更新每一层的权重参数。在反向传播中,通过计算梯度,可以得到每个神经元的误差,进而调整其权重和偏置,以最小化损失函数。
前向传播
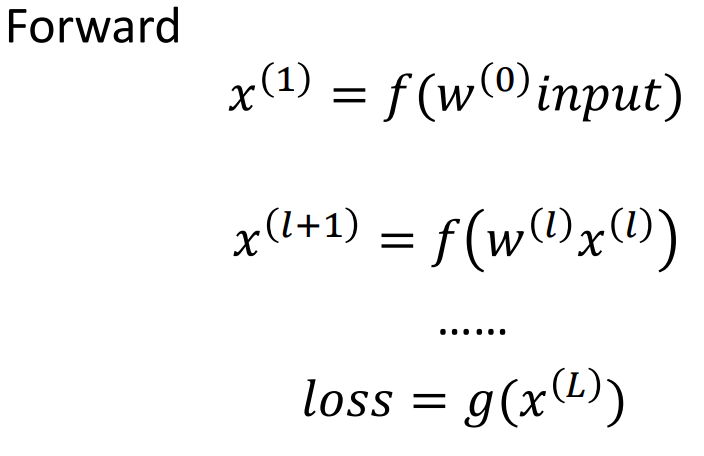
反向传播

-
𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 = 𝑔’(𝑥𝐿)
这个公式表示输出层对输入层的偏导数,它等于激活函数关于输入的导数,即𝑔’。 -
𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿−1 = 𝑊𝐿−1 · (𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1))
这个公式表示倒数第L-1层对第L层的偏导数,它等于第L层权重矩阵𝑊𝐿−1乘以(𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1)),其中𝑓’表示激活函数的导数。 -
𝜕𝑙𝑜𝑠𝑠/𝜕𝑤𝐿−1 = (𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1)) · 𝑥𝐿−1
这个公式表示对第L-1层的权重𝑤𝐿−1求偏导数,它等于(𝜕𝑙𝑜𝑠𝑠/𝜕𝑥𝐿 ⊙ 𝑓’(𝑊𝐿−1𝑥𝐿−1))乘以第L-1层的输入𝑥𝐿−1。
这些公式描述了反向传播算法中的梯度计算过程,它们用于更新神经网络中的权重以最小化损失函数。
梯度下降
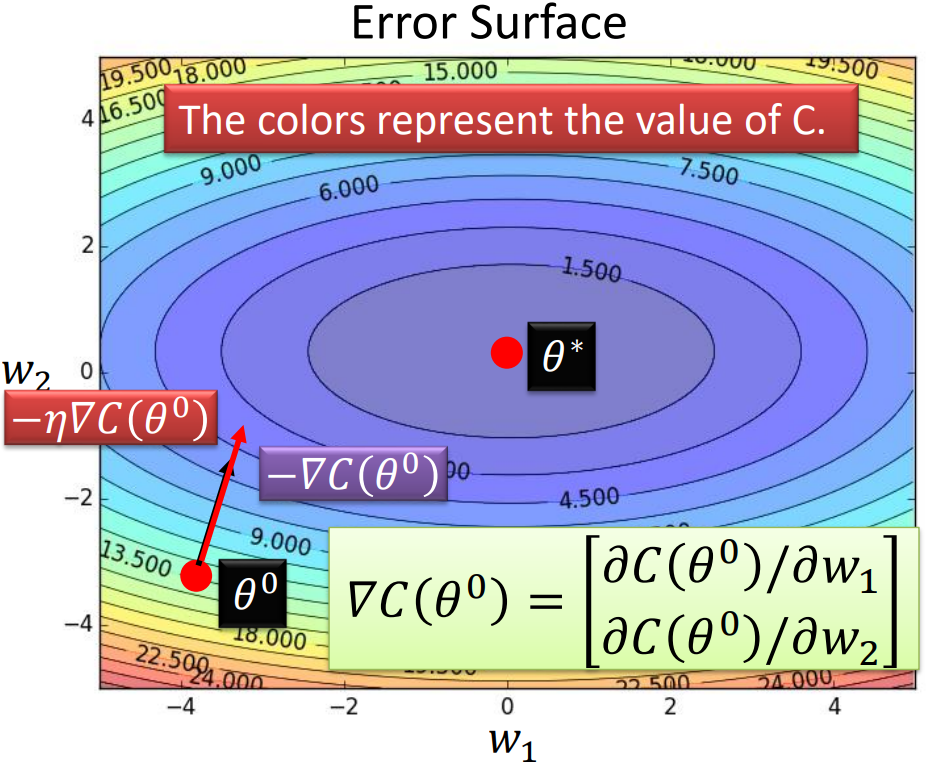
假设神经网络中只有两个参数 w 1 w_1 w1 和 w 2 w_2 w2。在梯度下降算法中,我们通过计算损失函数 C C C 关于参数的偏导数来确定梯度方向,并乘以学习率 η \eta η 来确定参数更新的步幅。这样反复迭代更新参数,直到达到收敛或满足停止条件。
具体步骤如下:
- 随机选择一个起始点 θ 0 \theta_0 θ0。
- 计算在 θ 0 \theta_0 θ0 处的负梯度 − ∇ C ( θ 0 ) -\nabla C(\theta_0) −∇C(θ0)。
- 将负梯度与学习率 η \eta η 相乘。
- 更新参数:
θ 0 = θ 0 − η ⋅ ∇ C ( θ 0 ) \theta_0 = \theta_0 - \eta \cdot \nabla C(\theta_0) θ0=θ0−η⋅∇C(θ0)
其中, ∇ C ( θ 0 ) \nabla C(\theta_0) ∇C(θ0) 是损失函数关于参数的偏导数组成的梯度。在二维空间中,可以表示为 ∇ C ( θ 0 ) = ( ∂ C ( θ 0 ) ∂ w 1 , ∂ C ( θ 0 ) ∂ w 2 ) \nabla C(\theta_0) = \left(\cfrac{\partial C(\theta_0)}{\partial w_1}, \cfrac{\partial C(\theta_0)}{\partial w_2}\right) ∇C(θ0)=(∂w1∂C(θ0),∂w2∂C(θ0))。
通过不断迭代更新参数,我们可以优化网络的性能,使损失函数最小化。

局部最小值
梯度下降算法并不保证能够达到全局最小值。不同的初始点 θ 0 \theta_0 θ0 可能会收敛到不同的局部最小值,因此会得到不同的结果。
这是因为神经网络的损失函数通常是非凸的,存在多个局部最小值。在非凸损失函数的情况下,梯度下降可能会陷入局部最小值而无法达到全局最小值。这就是为什么在训练神经网络时,初始点的选择非常重要。
然而,尽管梯度下降可能无法找到全局最小值,但在实际应用中,局部最小值往往已经足够好。此外,使用正则化和其他技巧可以帮助提高算法的鲁棒性,减少陷入不良局部最小值的风险。
因此,虽然非凸损失函数可能带来挑战,但梯度下降仍然是一种有效的优化方法,广泛应用于训练神经网络和其他机器学习模型中。
多层前馈网络表示能力
只需要一个包含足够多神经元的隐层, 多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数
多层前馈网络局限
• 神经网络由于强大的表示能力, 经常遭遇过拟合. 表现为:训练误差持续降低, 但测试误差却可能上升
• 如何设置隐层神经元的个数仍然是个未决问题. 实际应用中通常使用“试错法”调整
缓解过拟合的策略
• 早停:在训练过程中, 若训练误差降低, 但验证误差升高, 则停止训练
• 正则化:在误差目标函数中增加一项描述网络复杂程度的部分, 例如连接权值与阈值的平方和
相关文章:

【人工智能】— 神经网络、前向传播、反向传播、梯度下降、局部最小值、多层前馈网络、缓解过拟合的策略
【人工智能】— 神经网络、前向传播、反向传播 前向传播反向传播梯度下降局部最小值多层前馈网络表示能力多层前馈网络局限缓解过拟合的策略 前向传播和反向传播都是神经网络训练中常用的重要算法。 前向传播是指将输入数据从输入层开始经过一系列的权重矩阵和激活函数的计算后…...
小文智能自定义变量详解
在小文交互场景设计时,有一个特殊功能,叫做自定义变量。有时,根据外呼对象的不同,需要对用户传达不同的内容,比如称呼、地址、公司名称等等。此时,就可以使用小文交互的自定义变量功能来实现对不同用户呼出…...
平面电磁波的反射与折射,极化滤波作用
目录 引言 反射定律和折射定律 反射系数和折射系数 平面电磁波在理想介质分界面上的全反射和全折射 全反射 全折射 极化滤波作用 平面电磁波在良导体上的反射与折射 引言 再复杂的电磁波我们都可以看作是很多平面电磁波的叠加 我们在前面介绍的时候,我们认…...

键盘当鼠标用
当鼠标坏掉又需要使用电脑时发现触控板也不能用这就很烦那么键盘当鼠标用教程来了 使用键盘当鼠标的步骤如下: 1. 按住“AltShiftNum Lock”快捷键,弹出鼠标键开启咨询框,点击“是”按钮。 小键盘的数字就是方向/和*就是左右键切换5是单击 …...

动态规划part9 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
文章目录 198.打家劫舍思路思路代码官方题解代码 213.打家劫舍II思路思路代码官方代码困难 337.打家劫舍III思路思路代码官方题解代码困难 今日收获 198.打家劫舍 198.打家劫舍 思路 dp含义,偷前i个房,切第i个房偷 dp[i]max(dp[i-2],dp[i-3])nums[i] …...
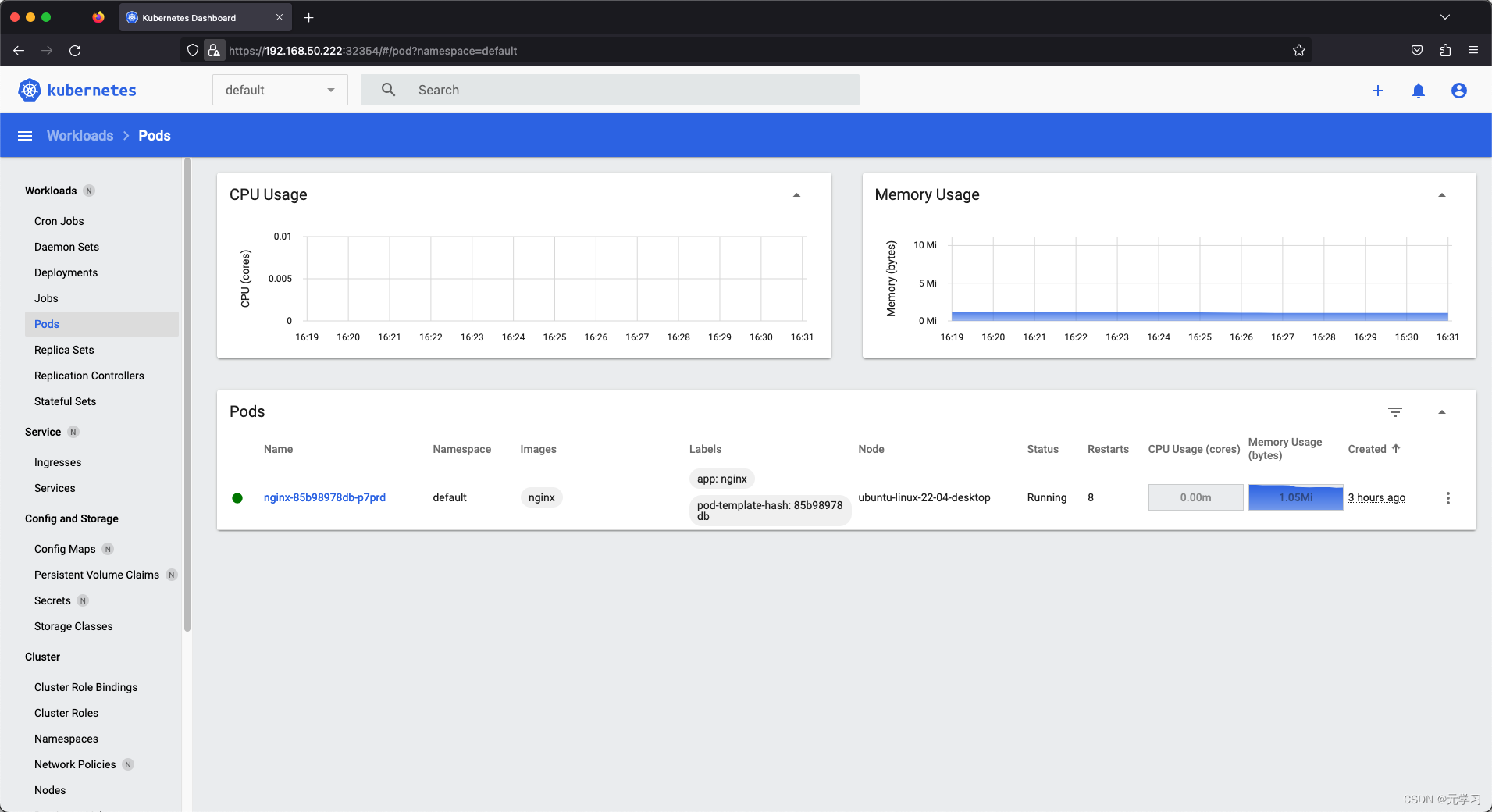
【k8s系列】一分钟搭建MicroK8s Dashboard
本文基于上一篇文章的内容进行Dashboard搭建,如果没有看过上一篇的同学请先查阅上一篇文章 k8s系列】使用MicroK8s 5分钟搭建k8s集群含踩坑经验 使用MicroK8s搭建Dashboard很简单,只需要在Master节点按照以下几步操作 1.启用Dashboard插件 microk8s en…...
ArcEngine二次开发0——入门(下载 部署 组件学习)
折腾一下ArcGIS Engine二次开发。 目录 1、开发环境配置2、部署一个ArcGIS Engine应用程序3、ArcObject组件学习4、报错及解决4、其他 1、开发环境配置 参考:https://blog.csdn.net/H48662654/article/details/113384150 (使用ArcEngine前,…...
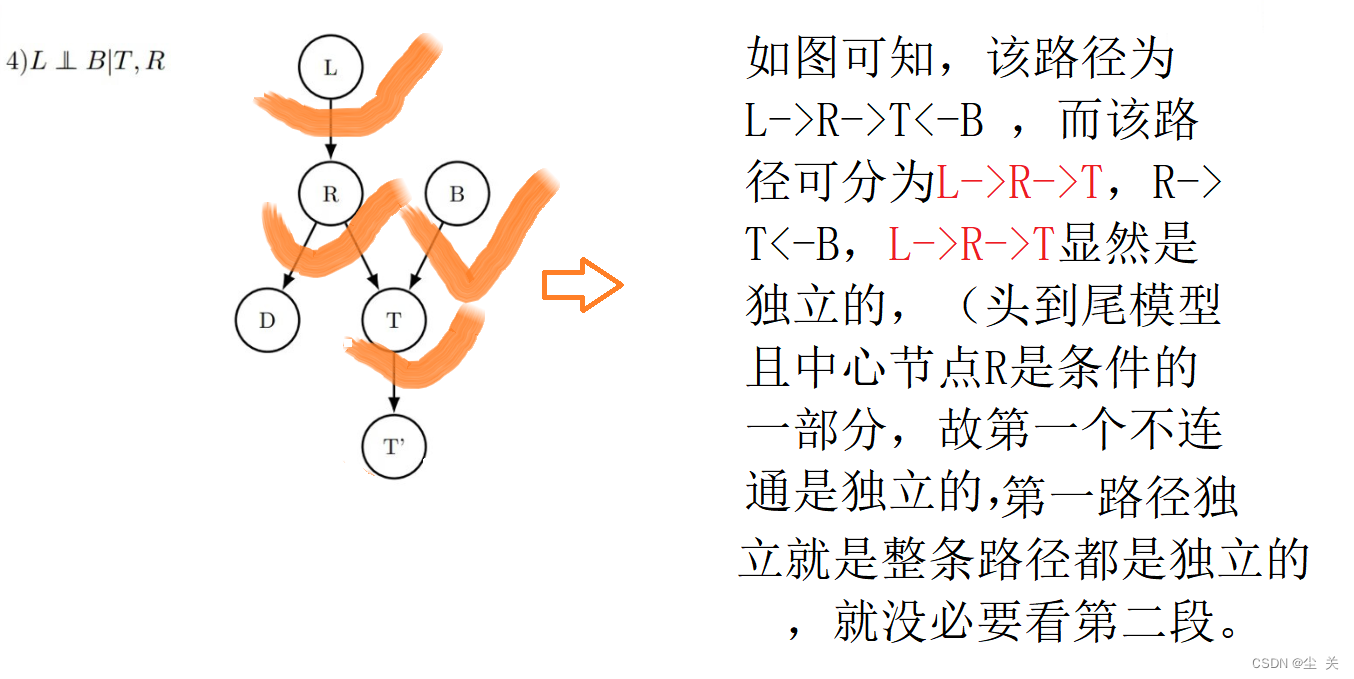
人工智能---D分离
D分离(D-Separation)是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点…...
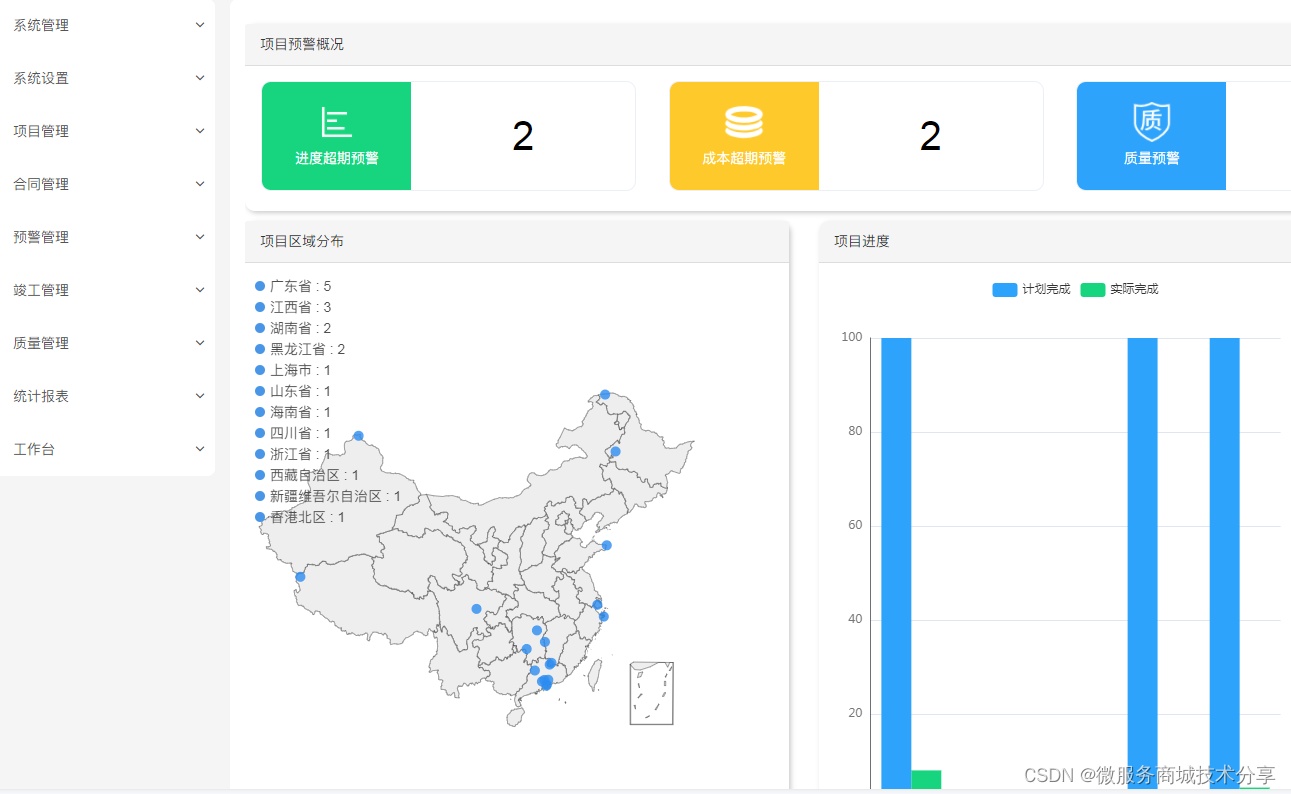
java spring cloud 企业工程项目管理系统源码-全面的工程项目管理
工程项目管理系统是指从事工程项目管理的企业(以下简称工程项目管理企业)受业主委托,按照合同约定,代表业主对工程项目的组织实施进行全过程或若干阶段的管理和服务。 如今建筑行业竞争激烈,内卷严重,…...

2023最新软件测试面试题【1000道题含答案】
1、自动化代码中,用到了哪些设计模式? 单例设计模式 工厂模式PO设计模式数据驱动模式面向接口编程设计模式 2、什么是断言( Assert) ? 断言Assert用于在代码中验证实际结果是不是符合预期结果,如果测试用例执行失败会抛出异常并提供断言日志 3、什么是web自动化测…...

【目标跟踪】MOT数据集GroundTruth可视化
MOT数据集格式简介 MOT15数据集下载:https://pan.baidu.com/s/1foGrBXvsanW8BI4eybqfWg?pwd8888 以下为一行gt示例: 1,1,1367,393,73,225,1,-1,-1,-1 各列数据对应含义如下 <frame>,<id>,<bb_left>,<bb_top>,<bb_width&g…...

软件测试的概念与过程----学习软件测试前的思考
软件测试的概念与过程----学习软件测试前的思考 1、软件测试工作是做什么的?2、那我做软件测试拿到一个软件产品我应该从哪里测试,怎末开始工作?3、测试早做好还是晚一些做好?4、软件测试能将软件测试的一点问题都没有嘛ÿ…...

Streamlit基础教程
streamlit是什么 streamlit是一个开源的python库,它能够快速的帮助我们创建定制化的web应用,而且还非常便于和他人分享,特别是在机器学习和数据科学领域。整个过程不需要你了解任何前端的知识,包括html、css、javascript等&#x…...

内网穿透技术
文章目录 前言1. 安装JAVA2. MCSManager安装3.局域网访问MCSM4.创建我的世界服务器5.局域网联机测试6.安装cpolar内网穿透7. 配置公网访问地址8.远程联机测试9. 配置固定远程联机端口地址9.1 保留一个固定tcp地址9.2 配置固定公网TCP地址9.3 使用固定公网地址远程联机 转载自内…...

计算机网络笔记:内部网关协议RIP
文章目录 1.协议RIP的工作原理2.距离向量算法3.坏消息传播得慢 1.协议RIP的工作原理 RIP的地位:RIP是内部网关协议IGP中最先得到广泛使用的协议,其中文译名为路由信息协议。 RIP概述: RIP是一种分布式的基于距离向量的路由选择协议&#x…...
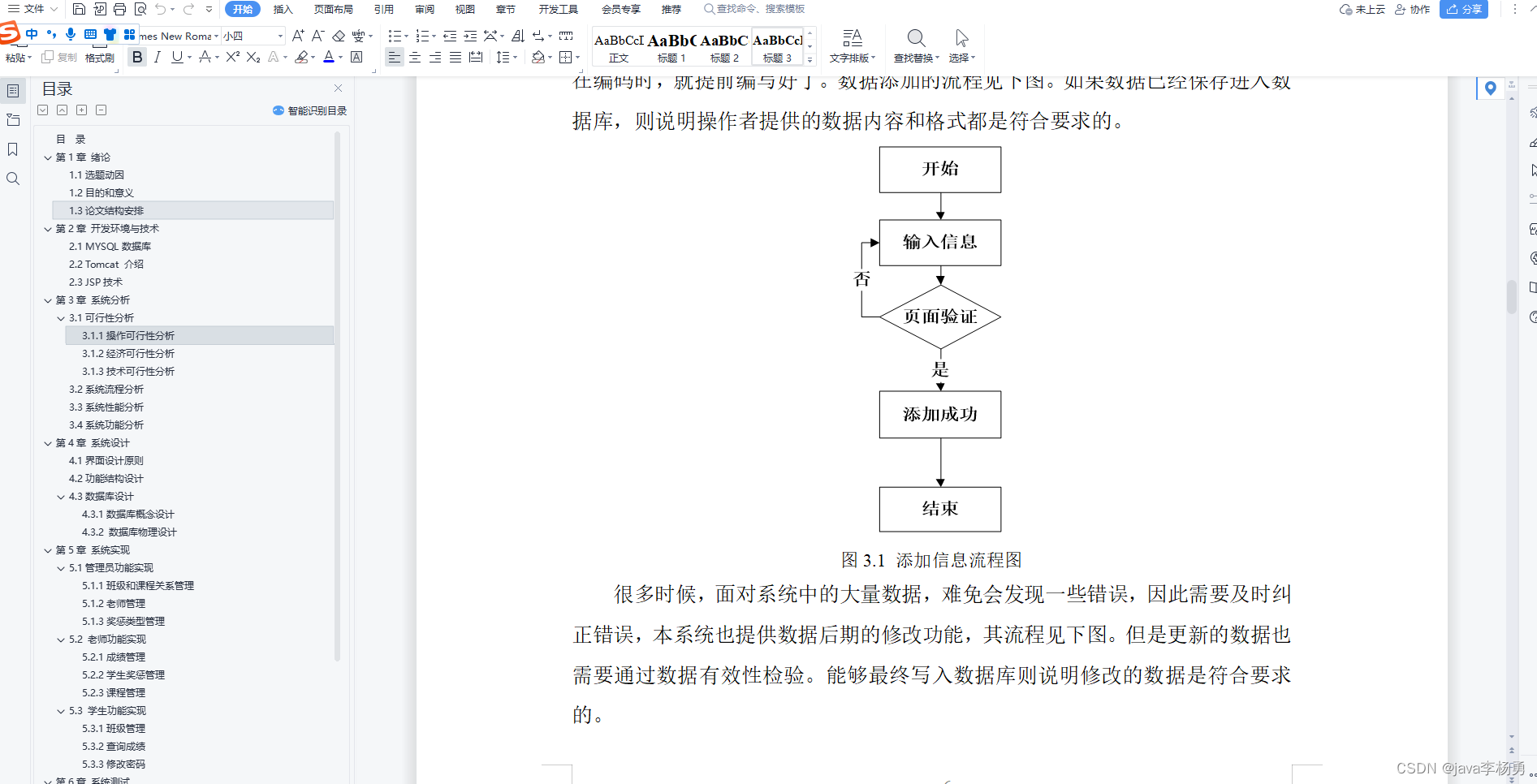
基于Java学生信息管理系统设计实现(源码+lw+部署文档+讲解等)
博主介绍: ✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精…...

PHP简单入门
PHP是一种流行的服务器端编程语言,被广泛用于Web开发。许多著名的网站和应用程序都是使用PHP编写的,例如Facebook、Wikipedia和WordPress等。本篇文章将为您介绍如何入门PHP编程。 环境配置 在开始使用PHP之前,需要先配置开发环境。要在本…...

java 客户端操作HDFS
1、windows上部署hadoop包 部署包win版本 源码包zip包 lib整合:共121个jar包 $HADOOP_PREFIX/share/hadoop/{common,hdfs,mapreduce,yarn,tools}/{lib,.}*.jar 将windows版本hadoop/bin/hadoop.dll 放到c:/windows/system32下 2、windows环境变量配置 hadoop的…...

区块链中的共识机制以及共识算法
目录 什么是共识 什么是共识机制 共识机制类型 1、基于工作证明(Proof of Work PoW)...

【计算机网络自顶向下】DNS简答题总结
主要功能:将域名解析为主机能识别的IP地址 DNS实现的功能 主机到IP地址的转换主机别名的转换邮件服务器别名负载均衡 DNS实现冗余服务器:一个IP地址集合对应同一个规范主机名 域名系统 分布式数据库:一个由多层DNS服务器实现的分布式数据库应…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
