线性代数行列式的几何含义
行列式可以看做是一系列列向量的排列,并且每个列向量的分量可以理解为其对应标准正交基下的坐标。
行列式有非常直观的几何意义,例如:
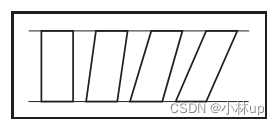
二维行列式按列向量排列依次是 a \mathbf{a} a和 b \mathbf{b} b,可以表示 a \mathbf{a} a和 b \mathbf{b} b构成的平行四边形的面积
∣ a b ∣ = ∣ ( x a x + y a y ) ( x b x + y b y ) ∣ = x a x b ∣ x x ∣ + x a y b ∣ x y ∣ + y a x b ∣ y x ∣ + y a y b ∣ y y ∣ = x a x b ( 0 ) + x a y b ( + 1 ) + y a x b ( − 1 ) + y a y b ( 0 ) = x a y b − y a x b . \begin{aligned} |\mathbf{a b}| & =\left|\left(x_{a} \mathbf{x}+y_{a} \mathbf{y}\right)\left(x_{b} \mathbf{x}+y_{b} \mathbf{y}\right)\right| \\ & =x_{a} x_{b}|\mathbf{x} \mathbf{x}|+x_{a} y_{b}|\mathbf{x y}|+y_{a} x_{b}|\mathbf{y} \mathbf{x}|+y_{a} y_{b}|\mathbf{y} \mathbf{y}| \\ & =x_{a} x_{b}(0)+x_{a} y_{b}(+1)+y_{a} x_{b}(-1)+y_{a} y_{b}(0) \\ & =x_{a} y_{b}-y_{a} x_{b} . \end{aligned} ∣ab∣=∣(xax+yay)(xbx+yby)∣=xaxb∣xx∣+xayb∣xy∣+yaxb∣yx∣+yayb∣yy∣=xaxb(0)+xayb(+1)+yaxb(−1)+yayb(0)=xayb−yaxb.
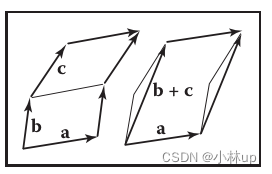
三维行列式按列向量排列依次是 a \mathbf{a} a, b \mathbf{b} b和 c \mathbf{c} c,可以表示 a \mathbf{a} a, b \mathbf{b} b和 b \mathbf{b} b构成的平行六面体的体积
∣ a b c ∣ = ∣ ( x a x + y a y + z a z ) ( x b x + y b y + z b z ) ( x c x + y c y + z c z ) ∣ = x a y b z c − x a z b y c − y a x b z c + y a z b x c + z a x b y c − z a y b x c . \begin{aligned} |\mathbf{a b c}| & =\left|\left(x_{a} \mathbf{x}+y_{a} \mathbf{y}+z_{a} \mathbf{z}\right)\left(x_{b} \mathbf{x}+y_{b} \mathbf{y}+z_{b} \mathbf{z}\right)\left(x_{c} \mathbf{x}+y_{c} \mathbf{y}+z_{c} \mathbf{z}\right)\right| \\ & =x_{a} y_{b} z_{c}-x_{a} z_{b} y_{c}-y_{a} x_{b} z_{c}+y_{a} z_{b} x_{c}+z_{a} x_{b} y_{c}-z_{a} y_{b} x_{c} . \end{aligned} ∣abc∣=∣(xax+yay+zaz)(xbx+yby+zbz)(xcx+ycy+zcz)∣=xaybzc−xazbyc−yaxbzc+yazbxc+zaxbyc−zaybxc.
相关文章:

线性代数行列式的几何含义
行列式可以看做是一系列列向量的排列,并且每个列向量的分量可以理解为其对应标准正交基下的坐标。 行列式有非常直观的几何意义,例如: 二维行列式按列向量排列依次是 a \mathbf{a} a和 b \mathbf{b} b,可以表示 a \mathbf{a} a和…...

python用flask将视频显示在网页上
注意我们的return返回值必须是以下之一,否则会报错 from flask import Flask, render_template, Response import cv2app Flask(__name__)app.route(/) def index():return render_template(index.html)def gen(camera):while True:success, image camera.read(…...
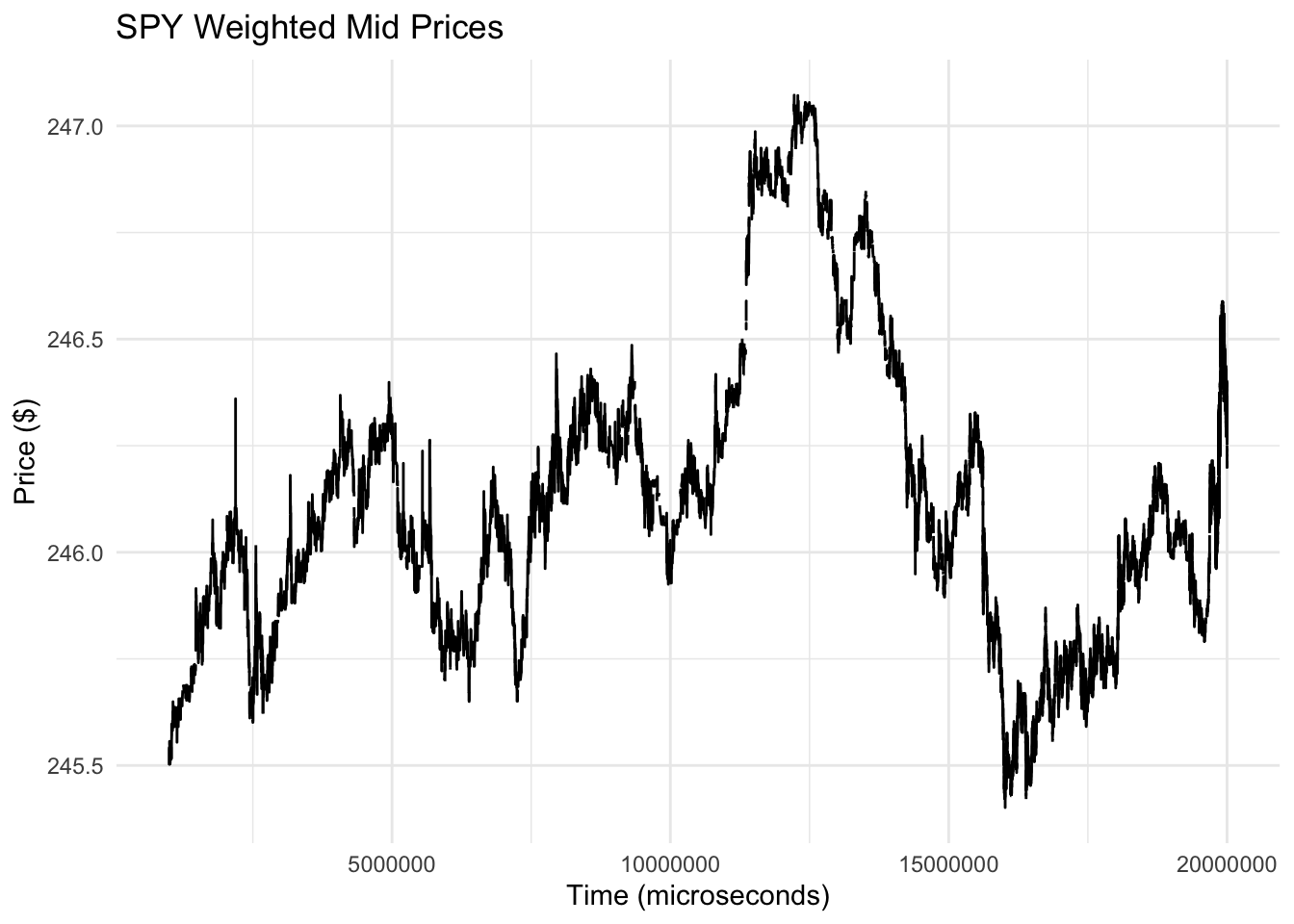
【数据挖掘】时间序列教程【一】
第一章 说明 对于时间序列的研究,可以追溯到19世纪末和20世纪初。当时,许多学者开始对时间相关的经济和社会现象进行研究,尝试发现其规律和趋势。其中最早的时间序列研究可以追溯到法国经济学家易贝尔(Maurice Allais)…...

优化索引粒度参数提升ClickHouse查询性能
当对高基数列进行过滤查询时,总是希望尽可能跳过更多的行。否则需要处理更多数据、需要更多资源。ClickHouse缺省在MergeTree表读取8192行数据块,但我们可以在创建表时调整该index_granularity 参数。本文通过示例说明如何调整该参数优化查询性能。 inde…...

selenium\webdriver\remote\errorhandler.py:242: SessionNotCreatedException问题解决
报错信息: raise exception_class(message, screen, stacktrace) E selenium.common.exceptions.SessionNotCreatedException: Message: session not created: This version of ChromeDriver only supports Chrome version 112 E Current browser versi…...
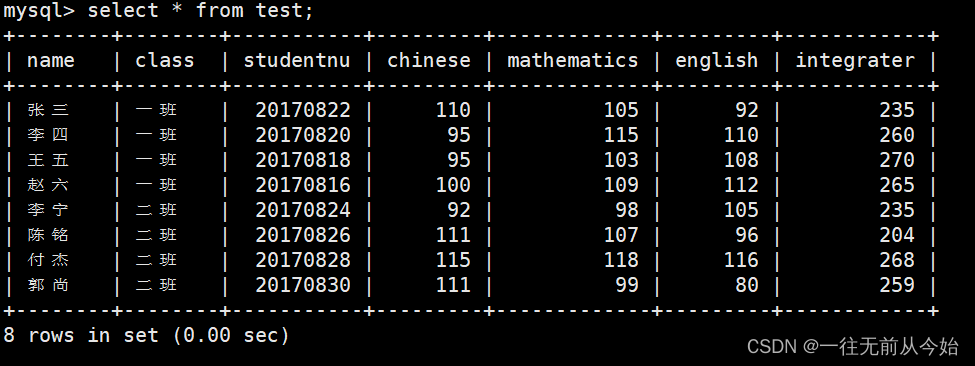
MySQL 备份与恢复
MySQL 备份与恢复 一、数据库备份的分类1.1 数据备份的重要性1.2 数据库备份的分类1.2.1 从物理与逻辑的角度,分为物理备份和逻辑备份1.2.2 从数据库的备份策略角度,分为完全备份,差异备份和增量备份1.2.3 常见的备份方法 二、MySQL完全备份与…...
js中改变this指向的三种方式
js中改变this指向的三种方式 1、call方法2、apply方法3、bind方法 1、call方法 使用 call 方法调用函数,同时指定函数中 this 的值,使用方法如下代码所示: <script>const obj {uname: 刘德华}function fn(x, y) {console.log(this) …...

小程序中如何进行数据传递和通信
103. 小程序中如何进行数据传递和通信? 1. 使用页面参数传递数据: 在小程序中,可以通过页面参数来传递数据。当跳转到一个新页面时,可以将需要传递的数据作为参数传入,然后在目标页面的onLoad函数中获取参数。 示例…...
Vue3项目中引入ElementUI使用详解
目录 Vue3项目中引入 ElementUI1.安装2.引入2.1 全局引入2.2 按需引入viteWebpack 3.使用 Vue3项目中引入 ElementUI ElementUI是一个强大的PC端UI组件框架,它不依赖于vue,但是却是当前和vue配合做项目开发的一个比较好的ui框架,其包含了布局…...

计算机启动
按下主机上的 power 键后,第一个运行的软件是 BIOS,BIOS 全称叫 Base Input & Output System,即基本输入输出系统。 (8086的1MB内存) 地址 0~0x9FFFF 处是 DRAM,顶部的 0xF0000~0xFFFFF&am…...
Unity学习笔记--EventSystem事件系统在使用上需要注意的地方(很基础,但是很多人会忘记!!!)
目录 前言代码Unity 场景配置运行报错分析解决办法拓展(预告) 前言 之前有写过一篇关于事件系统实现以及使用的文章 Unity学习笔记–C#事件系统的实现与应用 最近在使用的时候遇到了一些问题,所以在此记录下,也为看到这篇文章的人…...

高手必备:JVM调优的常用命令和参数一网打尽!
大家好,我是小米!在今天的技术分享中,我将和大家一起探讨JVM调优中的常用命令和参数。作为一名热爱技术的小伙伴,希望通过本篇文章的分享,能够帮助大家更好地理解和掌握JVM调优的方法和技巧。 JVM的结构 首先&#x…...

Uniapp 开发 ①(快速上手)
作者 : SYFStrive 博客首页 : HomePage 📜: UNIAPP开发 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 Ǵ…...

【数据库原理与实践】知识点归纳(下)
第6章 规范化理论 一、关系模式设计中存在的问题 关系、关系模式、关系数据库、关系数据库的模式 关系模式看作三元组:R < U,F >,当且仅当U上的一个关系r满足F时,r称为关系模式R < U,F >的一个关系 第一范式(1NF&…...

代码随想录day34
1005.K次取反后最大化的数组和 本题主要是想到排序的时候要按绝对值大小排序。 class Solution { static bool cmp(int a,int b){return abs(a)>abs(b); } public:int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(),nums.end(),cmp);…...

CSS知识点汇总(八)--Flexbox
1. flexbox(弹性盒布局模型)是什么,适用什么场景? 1. flexbox(弹性盒布局模型)是什么 Flexible Box 简称 flex,意为”弹性布局”,可以简便、完整、响应式地实现各种页面布局。采用…...

ASCII、Unicode、UTF-8、GBK
入门小菜鸟,希望像做笔记记录自己学的东西,也希望能帮助到同样入门的人,更希望大佬们帮忙纠错啦~侵权立删。 目录 一、定义 1、ASCII 2、Unicode 3、UTF-8 4、GB2312 5、GBK 6、\u和\x 二、相互转化 1、str 与 ASCII 2、str与utf-…...

【安全】使用docker安装Nessus
目录 一、准备docker环境服务器(略) 二、安装 2.1 搜索镜像 2.2 拉取镜像 2.3 启动镜像 三、离线更新插件 3.1 获取challenge 3.2 官方注册获取激活码 3.3 使用challenge码和激活码获取插件下载地址 3.4 下载的插件以及许可协议复制到容器内 四…...
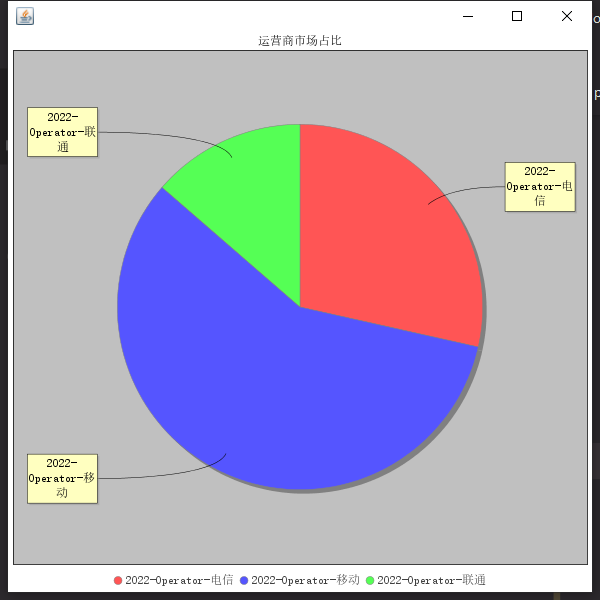
【Hadoop综合实践】手机卖场大数据综合项目分析
🚀 本文章实现了基于MapReduce的手机浏览日志分析 🚀 文章简介:主要包含了数据生成部分,数据处理部分,数据存储部分与数据可视化部分 🚀 【本文仅供参考!!非唯一答案】其中需求实现的…...
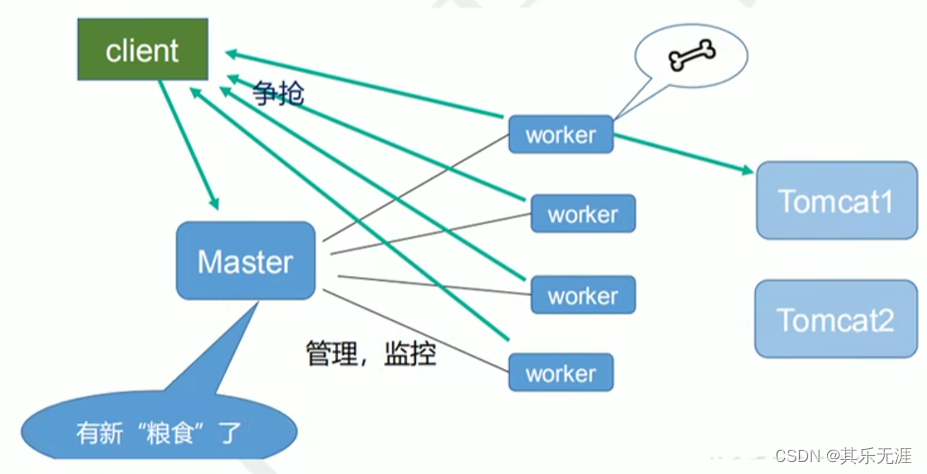
服务器技术(三)--Nginx
Nginx介绍 Nginx是什么、适用场景 Nginx是一个高性能的HTTP和反向代理服务器,特点是占有内存少,并发能力强,事实上nginx的并发能力确实在同类型的网页服务器中表现较好。 Nginx专为性能优化而开发,性能是其最重要的考量…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
