【备战秋招】每日一题:2023.03.26-阿里OD机试(第三题)-数组之和最小值
为了更好的阅读体检,可以查看我的算法学习网站
在线评测链接:P1119
题目内容
塔子哥是一个热爱数学的年轻数学家,他对数字和因子分解有着深入的研究。
有一天,他在一次偶然的探索中发现了一款神奇的游戏,名为“除数游戏”。
在这个游戏中,玩家需要在一个整数数组 a a a 中选择一个大于 1 1 1的数字 a i a_i ai ,并将其除以其中一个素因子 p p p (素因子是能被 a i a_i ai 整除的素数)。接着,玩家可以继续将新数字除以素因子,直到进行了 k k k 次操作。
塔子哥很快就意识到,这个游戏可以为他的研究提供很多有用的信息。他开始探究在最多进行 k k k 次操作的情况下,玩家能够通过该游戏达到的最小数组总和是多少?
输入描述
第一行输入两个正整数 n n n和 k k k,代表数组大小以及操作次数。
第二行输入 n n n个正整数 a i a_i ai,代表数组的元素。
1 ≤ n , k ≤ 200000 1\leq n,k\leq 200000 1≤n,k≤200000
1 ≤ a i ≤ 1 0 6 1\leq a_i\leq 10^6 1≤ai≤106
输出描述
一个整数,代表操作后的所有元素最小的和。
样例
输入
5 2
1 2 3 4 5
输出
9
思路
贪心+优先队列+数论优化
1.贪心策略:由于要最小化数组的总和,那么对于某一个数 a i a_i ai , 要除一定是除它最大的质因子 m a x f a c t o r ( a i ) maxfactor(a_i) maxfactor(ai)。 这样下降的最多,下降量为: Δ i = a i − m a x f a c t o r ( a i ) \Delta_i = a_i - maxfactor(a_i) Δi=ai−maxfactor(ai) 。所以显然每一次操作我们肯定是选择 m a x ( Δ i ) max(\Delta_i) max(Δi) 的位置 i i i 。然后还需要更新这个值。
2.引入高级数据结构:数据量比较大,为了能够快速实现我们这个贪心策略,我们需要一个可以快速 1.寻找最大值 2.删除最大值 3.插入值 的数据结构。这个显然可以使用优先队列维护。
3.引入数论优化:在优先队列的排序过程中,由于我们需要获取 m a x f a c t o r maxfactor maxfactor , 这个东西如果每次都暴力获得,复杂度为 O ( V ) O(\sqrt{V}) O(V) ,那么导致总复杂度为 O ( k ∗ l o g n ∗ V ) O(k*log n * \sqrt{V}) O(k∗logn∗V) 。 这是不可接受的(虽然期望复杂度无法达到这么高,但是我们总是希望有更优的解法!)。所以我们需要先预处理出 [ 1 , V = 1 e 6 ] [1,V=1e6] [1,V=1e6] 中的所有数的 m a x f a c t o r ( i ) maxfactor(i) maxfactor(i) 。
这个预处理方法,我们可以直接使用埃式筛的方法,转移伪代码如下:
for i in 2 ... V:if maxfactor[i] : continuefor j in i -> V , step = imaxfactor[j] = max(maxfactor[j] , i)
这样一来,
m a x f a c t o r ( i ) = { 0 i ∈ p r i m e m a x P r i m e F a c t o r o f i o t h e r \Large maxfactor(i)=\left\{\begin{matrix} 0 & i\ \in\ prime\\ maxPrimeFactor\ of\ i & other \end{matrix}\right. maxfactor(i)=⎩ ⎨ ⎧0maxPrimeFactor of ii ∈ primeother
最后,如果用一句话解释这个题的本质,就是TopK变种罢了 , 具体细节见代码!
类似题目推荐
LeetCode
见 贪心 - 代码随想录 . 这个只是入门,刷完也并不意味着能做出这题。
CodeFun2000
提供一些贪心题
P1014 2022.10.8-美团春招-塔子玩游戏
开胃菜1
P1211 塔子大厂真题模拟赛-第一题-魔法石(Ⅰ)
开胃菜2
P1279 2023.05.06-春招-第三题-塔子哥的游戏
同样是贪心 + 优先队列的经典题目!推荐做一做!
P1239 2023.04.20-华为od-第一题-总最快检测效率
同样是贪心 + 优先队列的经典题目!推荐做一做!
P1148 2023.4.3-阿里巴巴-研发岗-第三题-又一个数论题
虽然不是贪心题。但是也是常见算法套上了数论的优化!
代码
CPP
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 +5;
#define ll long long
int f[maxn] , a[maxn];
// 优先队列的节点
struct Node {int x;// 定义顺序bool operator < (const Node & a) const {int g1 = x - x / f[x];int g2 = a.x - a.x / f[a.x];// 优先下降量大的放堆顶return g1 < g2;}
};
priority_queue<Node> q;
int main (){int n , k;// f 就是 上文的maxfactor , 即最大质因数f[1] = 1;for (int i = 2 ; i < maxn ; i++){if (f[i] != 0) continue;for (int j = i ; j < maxn ; j += i){f[j] = max(f[j] , i);}}cin >> n >> k;// 把a[i] 都放入堆,同时获得最大值ll sum = 0;for (int i = 1 ; i <= n ; i++){cin >> a[i];sum += a[i];q.push({a[i]});}// 模拟操作while (k--){// 每次从堆顶拿出下降量最多的元素Node g = q.top();q.pop();// 更新总和sum -= g.x;sum += g.x / f[g.x];// 重新放入堆q.push({g.x / f[g.x]});}// 输出总和cout << sum << endl;return 0;
}
python
from random import *
import sys
from collections import *
from math import *
from functools import *
from heapq import *def solve(n,k,arr):mx = max(arr)tot = sum(arr)#f 就是 上文的maxfactor , 即最大质因数f = list(range(mx+1))for i in range(2,mx+1):if f[i] != i: continuefor j in range(i*2,mx+1,i):f[j] = i hq = []# 先把所有元素的可能序列都先全部放到序列中for a in arr:while a > 1:hq.append(a//f[a]-a)a //= f[a]# 建堆heapify(hq)# 取前k大for _ in range(k):if not hq: break tot += heappop(hq)return tot # 读入
n, k = list(map(int,input().split()))
arr = list(map(int,input().split()))
print(solve(n,k,arr))
Java
import java.util.*;
public class Main {static int MAXN = 1000010;static int[] prime = new int[MAXN];public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int k = sc.nextInt();prime[1] = 1;PriorityQueue<Node> pq = new PriorityQueue<>();isPrime();// 先将n个数放入优先队列for (int i = 0; i < n; i++) {int x = sc.nextInt();Node node = new Node(x, prime[x]);pq.offer(node);}// 模拟while (k-- > 0){Node node = pq.poll();int data = node.data;int x = data / node.prime;pq.offer(new Node(x, prime[x]));}long ans = 0;while (!pq.isEmpty()){ans += pq.poll().data;}System.out.println(ans);}// 求最大素数private static void isPrime() {for (int i = 2; i < MAXN; i++){if (prime[i] == 0){for (int j = i; j < MAXN; j += i){prime[j] = i;}}}}// 自定义排序static class Node implements Comparable<Node>{int data;int prime;public Node(int data, int prime) {this.data = data;this.prime = prime;}@Overridepublic int compareTo(Node o) {// 下降量最大优先return (o.data - o.data / o.prime) - (this.data - this.data / this.prime);}}
}
Go
package mainimport ("container/heap""fmt"
)const maxn = 1e6 + 5type Node struct {x int
}type PriorityQueue []Nodefunc (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {g1 := pq[i].x - pq[i].x/f[pq[i].x]g2 := pq[j].x - pq[j].x/f[pq[j].x]// 优先下降量大的放堆顶return g1 > g2
}
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }func (pq *PriorityQueue) Push(x interface{}) {node := x.(Node)*pq = append(*pq, node)
}func (pq *PriorityQueue) Pop() interface{} {n := len(*pq)node := (*pq)[n-1]*pq = (*pq)[:n-1]return node
}var f [maxn]int
var a [maxn]intfunc main() {var n, k int// f 就是 上文的 maxfactor,即最大质因数f[1] = 1for i := 2; i < maxn; i++ {if f[i] != 0 {continue}for j := i; j < maxn; j += i {f[j] = max(f[j], i)}}fmt.Scan(&n, &k)// 把 a[i] 都放入堆,同时获得最大值var sum int64 = 0pq := make(PriorityQueue, n)for i := 0; i < n; i++ {fmt.Scan(&a[i])sum += int64(a[i])pq[i] = Node{a[i]}}heap.Init(&pq)// 模拟操作for i := 0; i < k; i++ {// 每次从堆顶拿出下降量最多的元素g := heap.Pop(&pq).(Node)// 更新总和sum -= int64(g.x)sum += int64(g.x / f[g.x])// 重新放入堆heap.Push(&pq, Node{g.x / f[g.x]})}// 输出总和fmt.Println(sum)
}func max(x, y int) int {if x > y {return x}return y
}
Js
注意:已知的OJ上的JavaScript都不提供优先队列,要手写优先队列,这里塔子哥提供一种实现。
// 基于堆实现优先队列 , 函数名参考Java实现的priorityQueue
class Pqueue {constructor(cpr) {this.queue = [];this.size = 0;this.cpr = cpr;}swap(i, j) {let tmp = this.queue[i];this.queue[i] = this.queue[j];this.queue[j] = tmp;}// 上浮swim() {let ch = this.queue.length - 1;while (ch !== 0) {let fa = Math.floor((ch - 1) / 2);const ch_node = this.queue[ch];const fa_node = this.queue[fa];if (this.cpr(ch_node, fa_node) < 0) {this.swap(ch, fa);ch = fa;} else {break;}}}// 下沉sink() {let fa = 0;while (true) {let ch_left = 2 * fa + 1;let ch_right = 2 * fa + 2;let ch_max;let ch_max_node;const fa_node = this.queue[fa];const ch_left_node = this.queue[ch_left];const ch_right_node = this.queue[ch_right];if (ch_left_node && ch_right_node) {// 注意这里应该要>=0,因为左边优先级高if (this.cpr(ch_left_node, ch_right_node) <= 0) {ch_max = ch_left;ch_max_node = ch_left_node;} else {ch_max = ch_right;ch_max_node = ch_right_node;}} else if (ch_left_node && !ch_right_node) {ch_max = ch_left;ch_max_node = ch_left_node;} else if (!ch_left_node && ch_right_node) {ch_max = ch_right;ch_max_node = ch_right_node;} else {break;}// 注意这里应该要>0,因为父优先级高if (this.cpr(ch_max_node, fa_node) < 0) {this.swap(ch_max, fa);fa = ch_max;} else {break;}}}// 向优先队列中加入元素offer(ele) {this.queue.push(ele);this.size++;this.swim();}// 取出最高优先级元素poll() {this.swap(0, this.queue.length - 1);this.size--;const ans = this.queue.pop();this.sink();return ans;}// 只使用最高优先级元素,不取出peek() {return this.queue[0];}
}// 正片const maxn = 1e6 + 5;
let f = new Array(maxn).fill(0);
let a = new Array(maxn).fill(0);let q = new Pqueue((a , b) => {let g1 = a - Math.floor(a / f[a]);let g2 = b - Math.floor(b / f[b]);return g2 - g1;
});
f[1] = 1;
for (let i = 2; i < maxn; i++) {if (f[i] !== 0) continue;for (let j = i; j < maxn; j += i) {f[j] = Math.max(f[j], i);}
}process.stdin.resume();
process.stdin.setEncoding("utf-8");
let input = "";
process.stdin.on("data", (data) => {input += data;return;
});
process.stdin.on("end", () => {const lines = input.trim().split("\n");var [n, k] = lines[0].split(" ").map(Number);var a = lines[1].split(' ').map(Number);let sum = 0;for (let i = 0 ; i < n; i++) {sum += a[i];q.offer(a[i]);}while (k--) {let x = q.poll();sum -= x;sum += Math.floor(x / f[x]);q.offer(Math.floor(x / f[x]));}console.log(sum);
});
题目内容均收集自互联网,如如若此项内容侵犯了原著者的合法权益,可联系我: (CSDN网站注册用户名: 塔子哥学算法) 进行删除
相关文章:
-数组之和最小值)
【备战秋招】每日一题:2023.03.26-阿里OD机试(第三题)-数组之和最小值
为了更好的阅读体检,可以查看我的算法学习网站 在线评测链接:P1119 题目内容 塔子哥是一个热爱数学的年轻数学家,他对数字和因子分解有着深入的研究。 有一天,他在一次偶然的探索中发现了一款神奇的游戏,名为“除数游戏”。 在…...

网站的SEO优化:提升搜索引擎可见性的关键步骤
93. 网站的SEO优化:提升搜索引擎可见性的关键步骤 SEO(Search Engine Optimization)是指通过优化网站的内容、结构、链接和其他因素,以提高网站在搜索引擎结果页面(SERP)中的排名和可见性的过程。 优化网…...

Spring Boot 中的服务注册是什么,原理,如何使用
Spring Boot 中的服务注册是什么,原理,如何使用 Spring Boot 是一个非常流行的 Java 后端框架,它提供了许多便捷的功能和工具,使得开发者可以更加高效地开发微服务应用。其中,服务注册是 Spring Boot 微服务架构中非常…...

spring.factories文件在Spring工程中的说明
说明 spring.factories 是 Spring Boot 框架中一个特殊的配置文件,它用于定义自动配置的实现类以及要注册的其他组件信息。该文件通常位于 META-INF/spring.factories 目录下,Spring Boot 在启动时会自动加载它并读取其中的配置信息。 spring.factorie…...
常见的自动化测试架构有哪些?
目录 前言 常见的自动化架构包括如下。 1.数据驱动测试 2.模块驱动测试 3.关键字驱动测试 优点: 缺点: 总结: 前言 一个自动化测试架构就是一个集成体系,其中定义了一个特殊软件产品的自动化测试规则。这一体系中包含测试…...
Revit中用自适应创建简单的瓦片族和切换构件的材质?
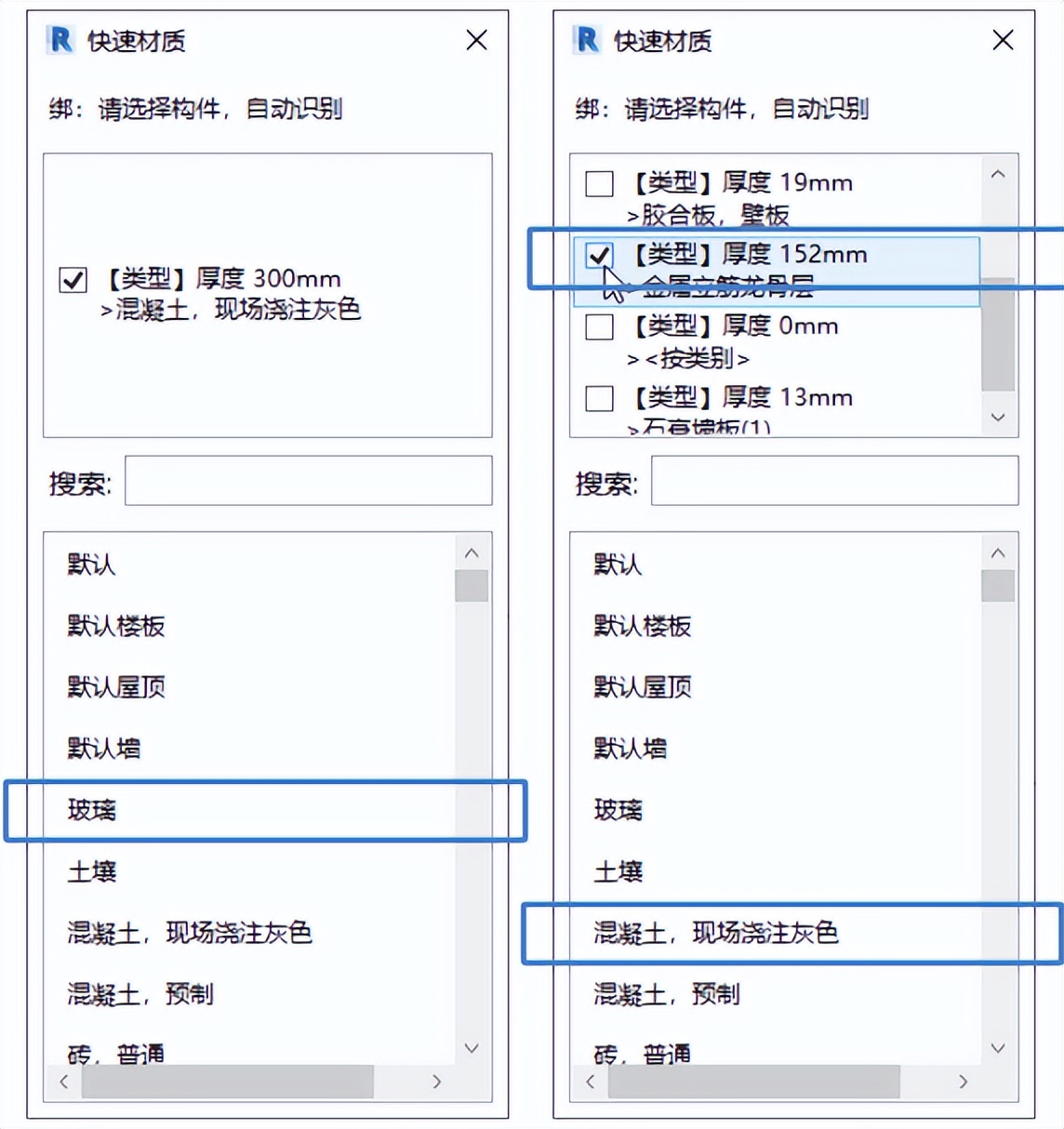
一、Revit中使用自适应创建瓦片族 在我们的日常生活中,屋顶的瓦片是我们经常都能够见到的,瓦片能够挡风遮雨也能够使建筑物带来古香古色的气息,那我们今天来学习如何使用自适应创建简单的瓦片族。 1.首先:我们打开自适应公制常规模…...
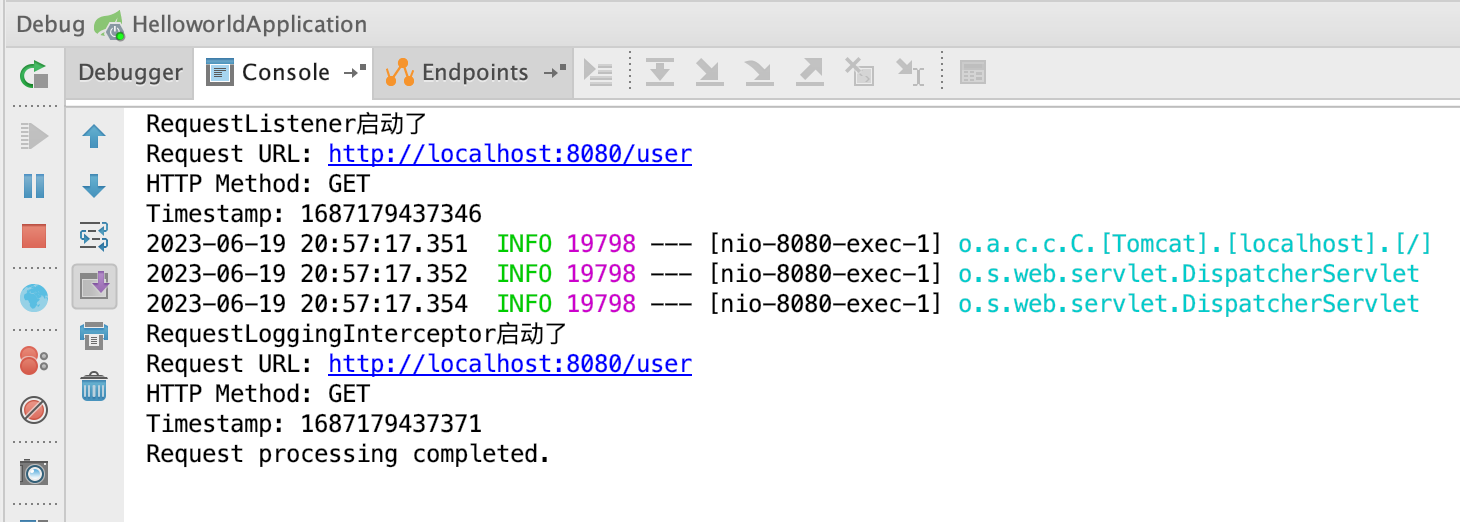
Spring Boot实战:拦截器和监听器的应用指南
当使用Spring Boot时,我们可以通过拦截器(Interceptor)和监听器(Listener)来实现对请求和响应的处理。拦截器和监听器提供了一种可插拔的机制,用于在请求处理过程中进行自定义操作,例如记录日志…...

为什么要搭建数据仓库
数据是企业中最重要的资源之一,因此,随着企业数据量的不断增大和复杂度的提高,建立一个可靠和健全的数据仓库变得越来越重要。在数聚股份看来,一个数据仓库可以作为一个企业数据存储和管理系统,能够更有效地存储、管理…...
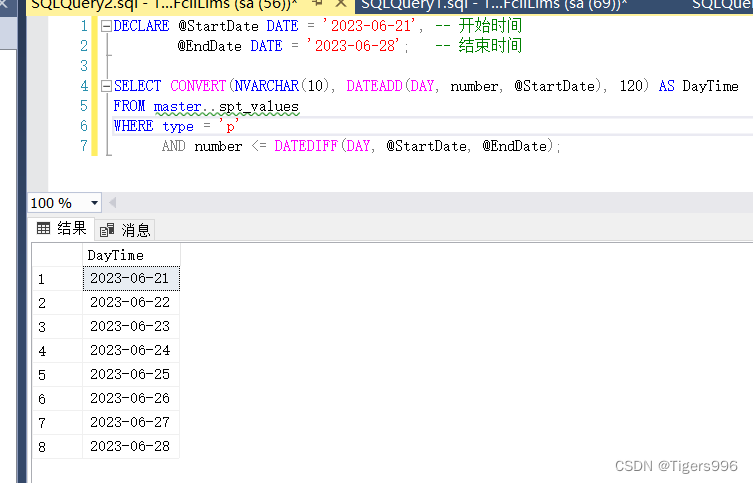
Sql Server 获取连续日期时间
获取连续日期时间 在项目中,有时候需要按日期/时间统计,例如2023-06-21至2023-06-28期间每一天的数据,如果某一天没有数据,也要查询出来,用NULL处理。 1.示例 2.连续日期效果SQL DECLARE StartDate DATE 2023-06-2…...
MIT 6.830数据库系统 -- lab two
MIT 6.830数据库系统 -- lab two 项目拉取Lab Two实现提示练习一 -- Filter and Join练习二 -- Aggregates练习三 -- HeapFile Mutability练习四 -- Insertion & deletion练习五 -- Page eviction练习六 -- Query walkthrough练习七 - 查询解析 项目拉取 原项目使用ant进行…...
)
React基础知识点(一)
React基础知识点 目标 能够说出React是什么能够说出React的特点能够掌握React的基本使用能够使用React脚手架 什么是React (★★★) React是一个用于构建用户界面的javaScript库,起源于facebook的内部项目,后续在13年开源了出…...
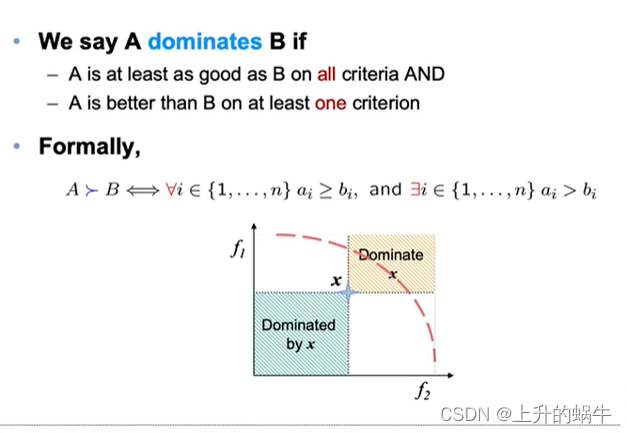
机器学习-进化算法
进化算法 遗传算法(Genetic Algorithm,GA)crossovermutation 进化策略(Evolutionary Strategies,ES)基因编程(Genetic Programming)Multi-objective Evolutionary Algorithms 遗传算…...
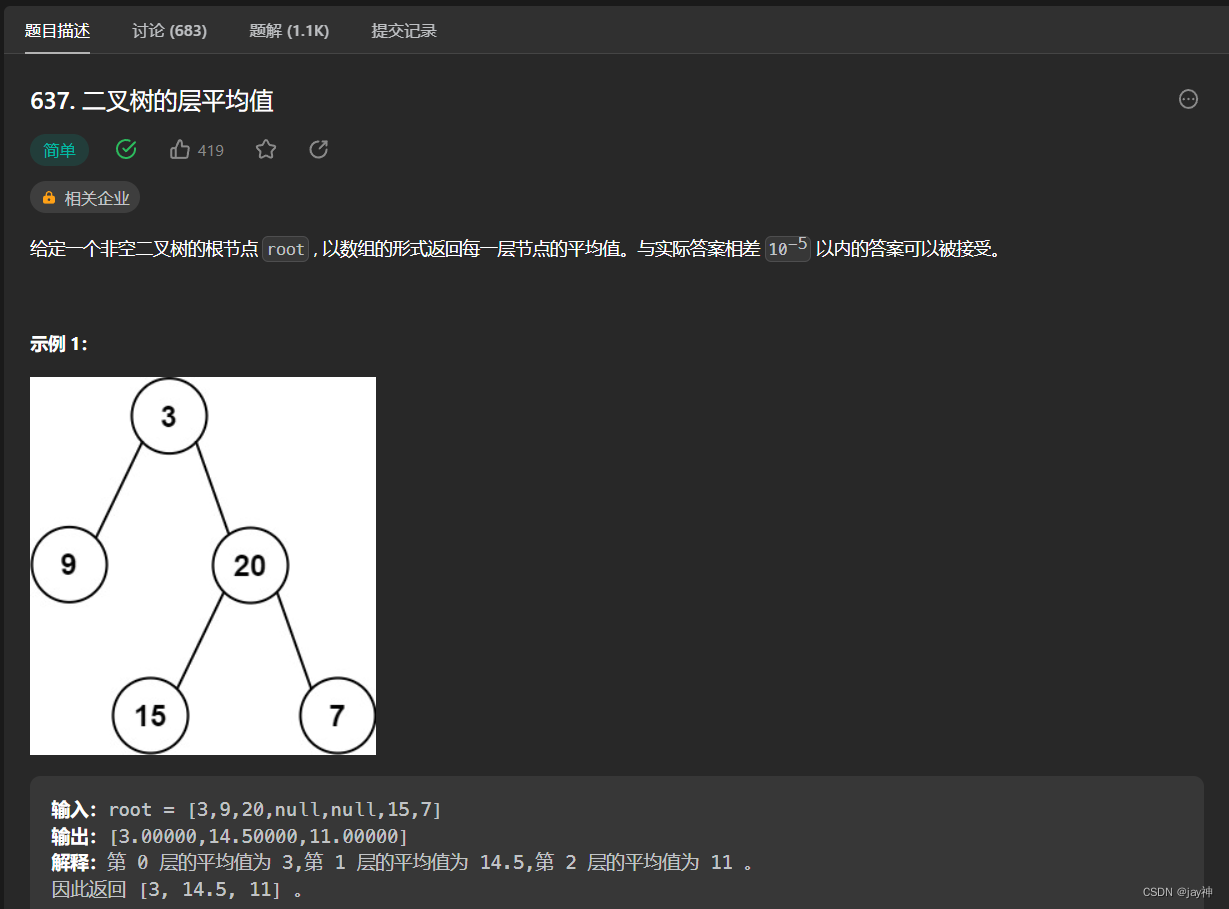
leetcode 637. 二叉树的层平均值
2023.6.29 依旧是层序遍历的变体,在层序遍历的代码中的内层循环求个和,然后出循环之后取个平均值即可实现层平均值,下面上代码: class Solution { public:vector<double> averageOfLevels(TreeNode* root) {vector<doub…...

7-数组创建函数还有哪些?【视频版】
目录 问题视频解答 问题 视频解答 点击观看: 7-数组创建函数还有哪些?...

webrtc源码阅读之P2P流程分析
P2P从宏观原理上其实就是: 收集本地Candidates设置远程Candidates连通性测试及排序 本文我们从Offer端的角度进行源码分析,学习webrtc是如何进行P2P连接的。版本m98。 一、收集本地Candidates examples/peerconnection中,CreateOffer以后&…...
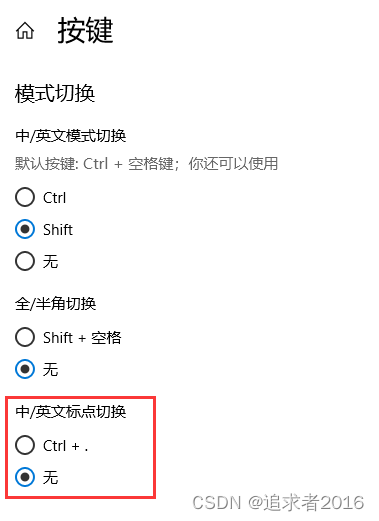
vscode 快速修复(quick fix) 快捷键(Ctrl + .)被占用问题解决方法
vscode 快速修复(quick fix) 快捷键(Ctrl .)被占用 微软拼音的中/英文标点切换的快捷键为Ctrl .,与 vscode 快速修复(quick fix)快捷键冲突。修复方法如下: 切换到微软拼音,在输入法中或英字上,点击右键。 再点设置 - 按键。 …...

阿里云——扩展Linux系统盘
扩展分区和文件系统_Linux系统盘 {#concept_ocb_htw_dhb .concept} 本文提供了如何使用growpart和resize2fs工具完成Linux系统盘分区扩容及文件系统扩展的操作指导。 适用范围 {#section_u9c_3g5_ljs .section} 本文的操作步骤适用于以下分区和文件系统格式的云盘࿱…...

TypeScript ~ 掌握基本类型 ②
作者 : SYFStrive 博客首页 : HomePage 📜: TypeScript ~ TS 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 &…...
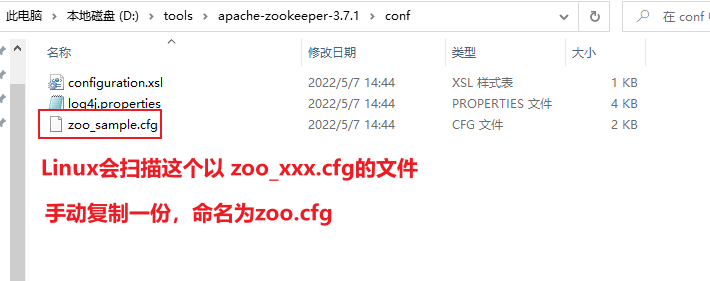
【Zookeeper】win安装随笔
目录 下载地址下载目标解压后目录结构配置文件配置文件详情伪分布式安装LinuxZooKeeper audit is disabled启动解决报错:SLF4J: Class path contains multiple SLF4J bindings. _ 下载地址 https://zookeeper.apache.org/releases.html 下载目标 记住选择带bin的…...
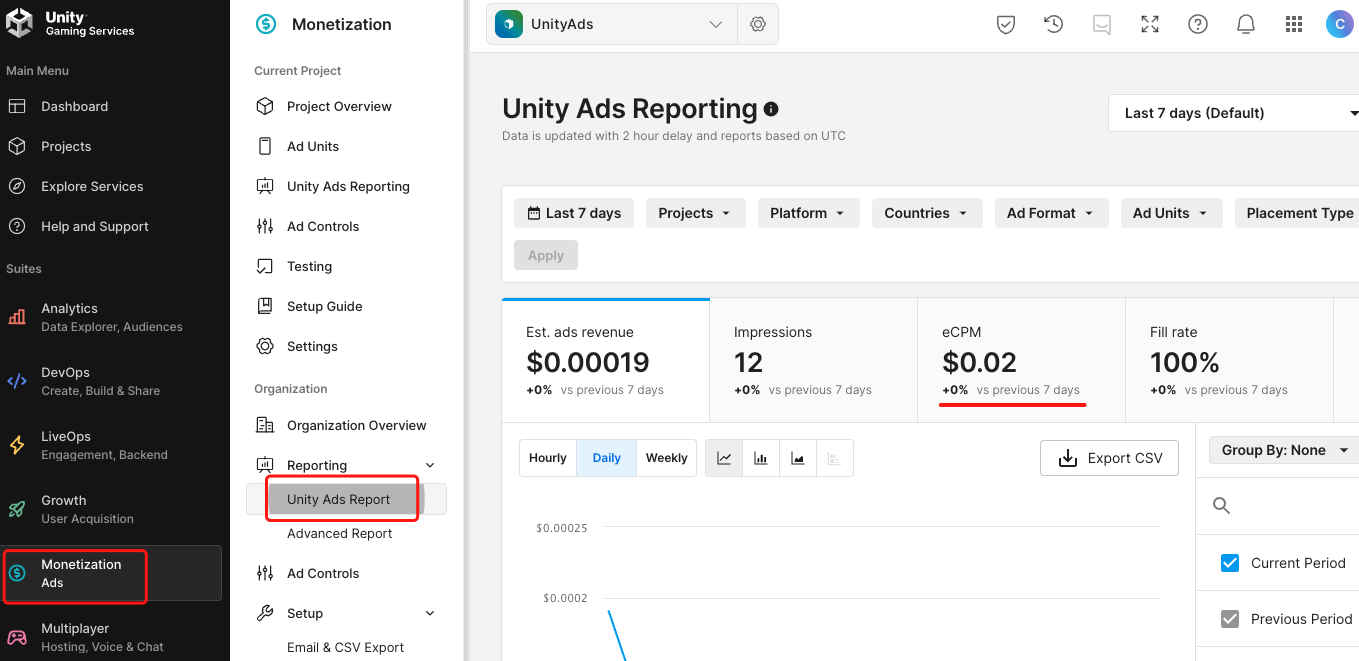
Unity 之 最新原生广告Ads接入 -- 助力增长游戏收益
Unity 之 最新Ads原生广告接入流程详解和工具类分享 一,注册 Unity Ads 广告 SDK二,下载 Unity Ads 广告 SDK三,配置 Unity Ads 广告 SDK3.1 广告位展示流程3.2 代码初始化 四,集成 Unity Ads 广告 SDK4.1 相关介绍4.2 代码分享 五…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

npm install 相关命令
npm install 相关命令 基本安装命令 # 安装 package.json 中列出的所有依赖 npm install npm i # 简写形式# 安装特定包 npm install <package-name># 安装特定版本 npm install <package-name><version>依赖类型选项 # 安装为生产依赖(默认&…...

C#和C++在编译过程中的文件区分
1. .h是头文件(Header File) 用来 声明类、函数、常量等。 通常不包含实际实现,只是“定义接口” // 示例:math_utils.h#pragma once int add(int a, int b); //定义函数名2. .cpp是源文件(Source File&…...

STM32+MPU6050传感器
#创作灵感## 在嵌入式系统开发中,STM32F103C8T6单片机与MPU6050传感器的组合因其高性能、低功耗以及丰富的功能而备受青睐。本文将简单介绍如何在Keil 5开发环境中实现STM32F103C8T6与MPU6050的连接和基本数据采集,带你快速入门智能硬件开发。 一、硬件…...
