【最短路+状压】CF1846 G
Problem - G - Codeforces
题意:

思路:

Code:
#include <bits/stdc++.h>//#define int long longusing namespace std;const int mxn=1e6+10;
const int mxv=1e6+10;
const int mxe=2e3+10;
const int mod=1e9+7;
const int Inf=0x3f3f3f3f;struct ty2{int x,dis;bool operator<(const ty2&a)const{return a.dis<dis;}
};priority_queue<ty2> Q;int N,M,st=0;
int d[mxn],e[mxn],se[mxn];
int vis[(1<<10)+10],dis[(1<<10)+10];char x;void dij(){memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));dis[st]=0;Q.push({st,0});while(!Q.empty()){auto u=Q.top();Q.pop();if(vis[u.x]) continue;vis[u.x]=1;for(int i=1;i<=M;i++){int w=d[i];int v=((u.x&(~e[i]))|se[i]);if(dis[v]>dis[u.x]+w){dis[v]=dis[u.x]+w;Q.push({v,dis[v]});}}}
}
void solve(){st=0ll;while(!Q.empty()) Q.pop();cin>>N>>M;for(int i=1;i<=M;i++){d[i]=e[i]=se[i]=0;}for(int i=0;i<N;i++){cin>>x;st|=((x=='1')<<i);}for(int i=1;i<=M;i++){cin>>d[i];e[i]=se[i]=0;for(int j=0;j<N;j++){cin>>x;e[i]|=((x=='1')<<j);}for(int j=0;j<N;j++){cin>>x;se[i]|=((x=='1')<<j);}}dij();if(dis[0]==Inf) cout<<-1<<'\n';else cout<<dis[0]<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;while(__--)solve();return 0;
}
相关文章:

【最短路+状压】CF1846 G
Problem - G - Codeforces 题意: 思路: Code: #include <bits/stdc.h>//#define int long longusing namespace std;const int mxn1e610; const int mxv1e610; const int mxe2e310; const int mod1e97; const int Inf0x3f3f3f3f;stru…...
vue+elementui实现英雄联盟道具城
目录 一、效果图 1.首页 2.商品列表、分类 二、实现重点讲解 1.首页轮播图 1.1技术实现: 1.2.鼠标聚焦切换图片事件 2.首页tab切换 3.商品列表实现 三、项目结构说明 四、总结 一、效果图 1.首页 项目与官方效果没有太大差异: 游戏导航࿱…...

ruby注释
在Ruby中,可以使用以下两种方式进行注释: 1. 单行注释:使用井号(#)在代码行的开头添加注释。例如: # 这是一个单行注释 puts "Hello, World!" 2. 多行注释:使用begin和end将多行注…...

2023(WAIC)智能驾驶科技峰会丨拓数派大模型下的数据计算系统,助力汽车智能化产业数据增值
2023 智能驾驶科技峰会在上海圆满落幕,本次大会由世界人工智能大会(WAIC)组委会办公室指导,浦东新区人民政府支持,浦东新区科技和经济委员会、中国 (上海)自由贸易试验区管理委员会金桥管理局主…...
牛客周赛 Round 2
小红的环形字符串小红的环形字符串 题目描述 小红拿到了一个环形字符串s。所谓环形字符串,指首尾相接的字符串。 小红想顺时针截取其中一段连续子串正好等于t,一共有多少种截法? 思路分析 环形问题。 将字符串 s 拼接自身,得到新…...
Git 命令提交和分支控制
强大的分支和合并:Git 提供了强大的分支功能,使得开发者可以轻松创建、合并和管理分支。这种灵活性使得团队可以同时进行多个任务和实验性开发,而不会相互干扰 Git 在处理大型代码仓库和版本历史时表现出色。它使用了一种称为“快照”的机制…...
2023 node 接入腾讯云短信服务,实现发送短信功能
1、在 腾讯云开通短信服务,并申请签名和正文模板 腾讯云短信 https://console.cloud.tencent.com/smsv2 a、签名即是短信的开头。例如 【腾讯云短信】xxxxxxx; b、正文模板即短信内容, 变量部分使用{1}, 数字从1开始累推。例如&a…...
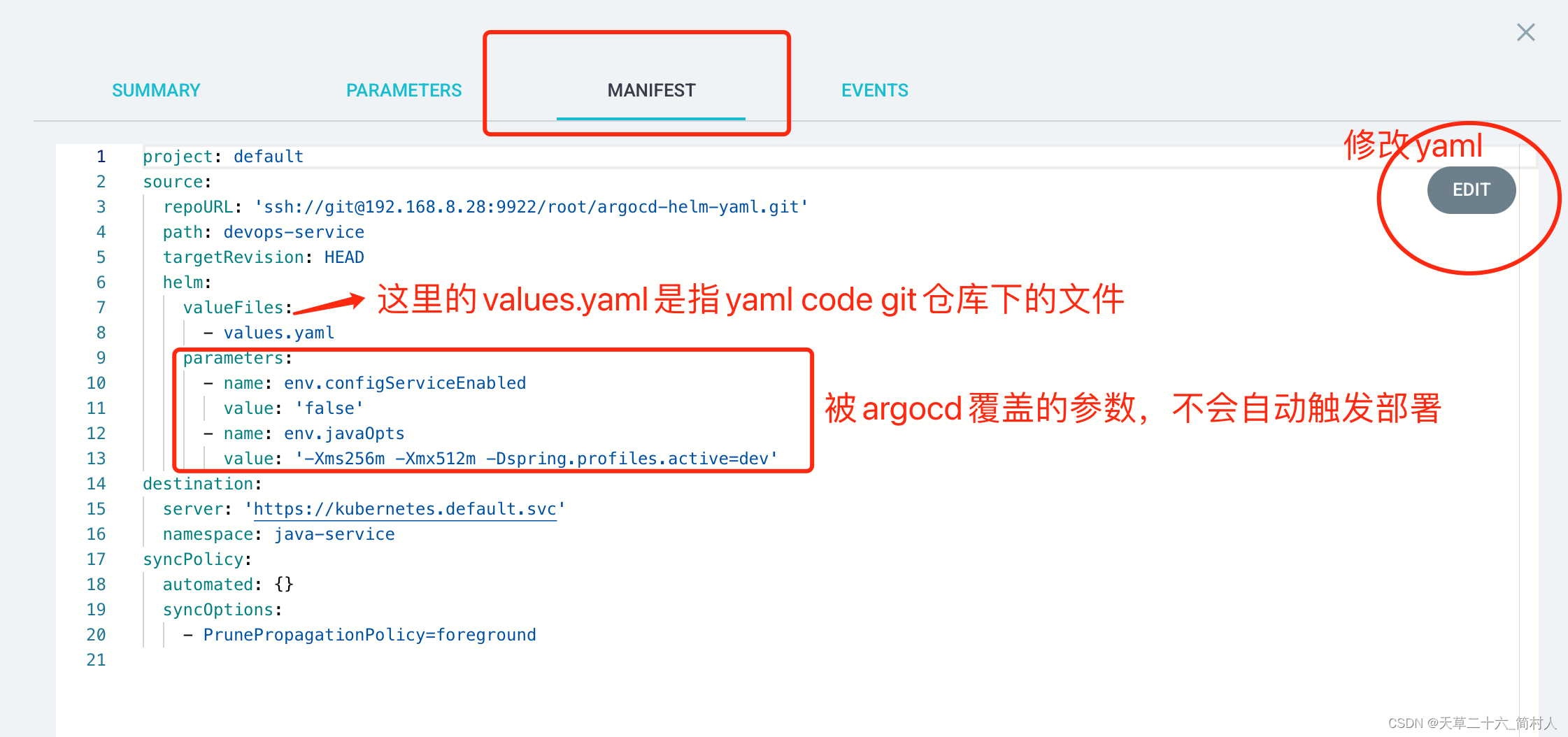
Devops系列四(使用argocd部署java应用到k8s容器)
一、说在前面的话 上文已为我们准备好了以下内容: 制作java应用的docker镜像,并推送至镜像仓库上传helm yaml代码至gitlab仓库(此gitlab和java应用所在的gitlab可以独立,也可以在一起,但是不宜在同一个工程ÿ…...
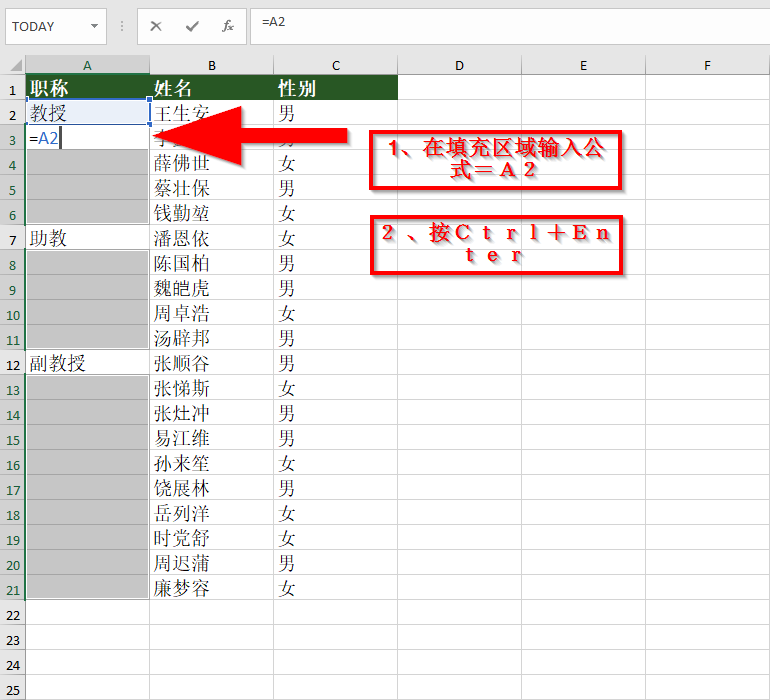
如何在Microsoft Excel中进行不连续区域批量填充
快速填充是 Excel 最令人惊叹的功能之一,它因让一个需要数小时手动执行的乏味任务瞬间自动执行而得名,然而它也有局限性: 结果不是动态的。当你更改其所基于的值时,快速填充值不会更新。你需要再次执行快速填充才能更新值。 快速填充可能并不总是返回结果。该模式对于 Exce…...

k8s+springboot+CronJob 定时任务部署
kubernetesspringbootCronJob 定时任务配置如下代码: cronjob.yaml k8s 文件 apiVersion: batch/v1 kind: CronJob metadata:name: k8s-springboot-demonamespace: rz-dt spec:failedJobsHistoryLimit: 3 #执行失败job任务保留数量successfulJobsHistoryLimit: 5 …...
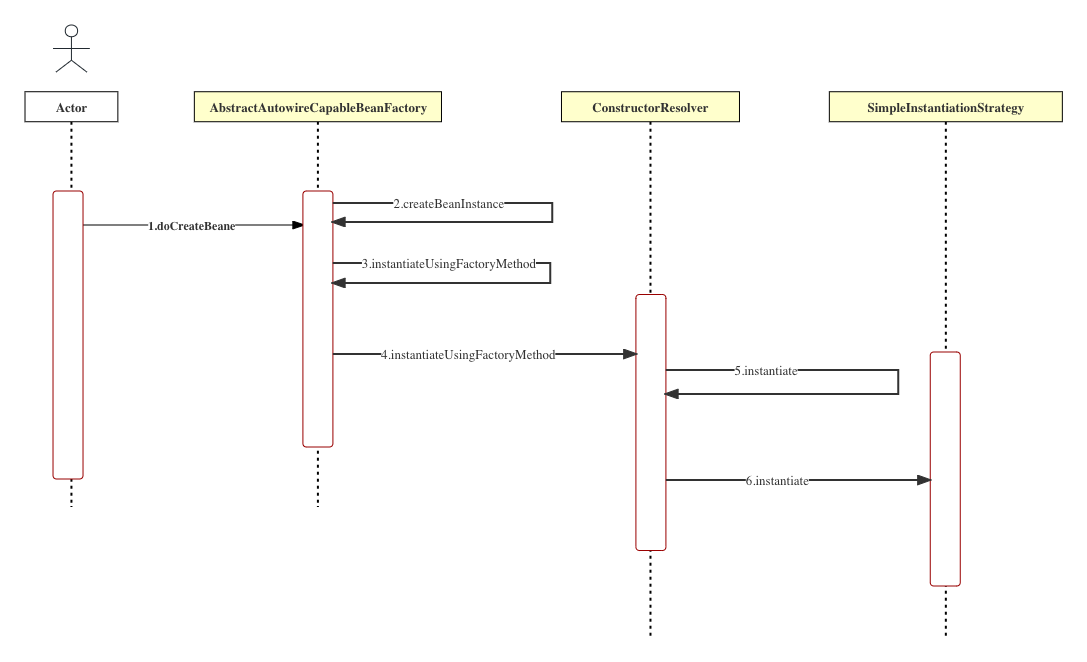
Spring5 中更优雅的第三方 Bean 注入
小伙伴们知道,当我们使用 Spring 容器的时候,如果遇到一些特殊的 Bean,一般来说可以通过如下三种方式进行配置: 静态工厂方法实例工厂方法FactoryBean 不过从 Spring5 开始,在 AbstractBeandefinition 类中多了一个属…...

Yolov5-Face 原理解析及算法解析
YOLOv5-Face 文章目录 YOLOv5-Face1. 为什么人脸检测 一般检测?1.1 YOLOv5Face人脸检测1.2 YOLOv5Face Landmark 2.YOLOv5Face的设计目标和主要贡献2.1 设计目标2.2 主要贡献 3. YOLOv5Face架构3.1 模型架构3.1.1 模型示意图3.1.2 CBS模块3.1.3 Head输出3.1.4 stem…...

通俗易懂讲解CPU、GPU、FPGA的特点
1. CPU vs GPU 大家可以简单的将CPU理解为学识渊博的教授,什么都精通;而GPU则是一堆小学生,只会简单的算数运算。可即使教授再神通广大,也不能一秒钟内计算出500次加减法。因此,对简单重复的计算来说,单单一…...

PIC18 DataRAM 笔记
1.疑似最糟糕的英文技术文档段落 Since up to 16 registers may share the same low-order address, the user must always be careful to ensure that the proper bank is selected before performing a data read or write. For example, writing what should be program dat…...
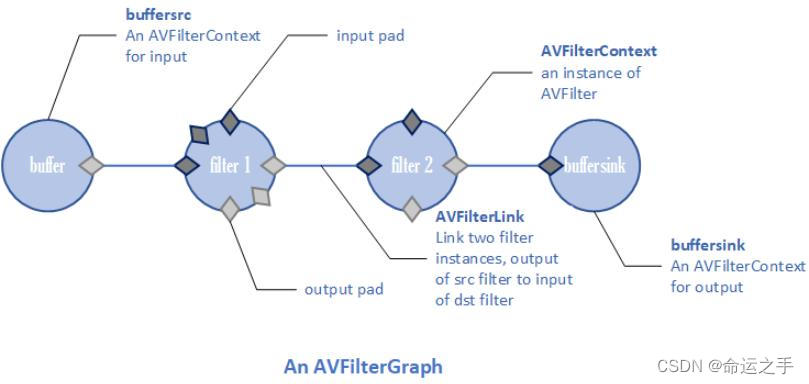
【FFMPEG】AVFilter使用流程
流程图 核心类 AVFilterGraph ⽤于统合这整个滤波过程的结构体 AVFilter 滤波器,滤波器的实现是通过AVFilter以及位于其下的结构体/函数来维护的 AVFilterContext ⼀个滤波器实例,即使是同⼀个滤波器,但是在进⾏实际的滤波时,也…...

爬虫入门06——了解cookie和session
爬虫入门06——了解cookie和session (1)什么是cookie,有什么作用 http请求是无状态的请求协议,不会记住用户的状态和信息,也不清楚你在这之前访问过什么而当网站需要记录用户是否登录时,就需要在用户登录…...

Ubuntu 的移动梦醒了
老实讲,移动版 Ubuntu 在手机、平板上的发展自始至终可能都没有达到过 Canonical 的期望,既然如此,不再勉为其难地坚持下去,或许才是更加明智的做法。 时至今日,官方显然也意识到了这一点,在早些时候发布的…...
RabbitMQ的集群
新建一个虚拟机,重新安装一个RabbitMQ,不会安装的可以看下面的连接: 在Linux中安装RabbitMQ_流殇꧂的博客-CSDN博客 1.修改/etc/hosts映射文件,两台虚拟机都需要修改 vim /etc/hosts 127.0.0.1 node1 localhost.localdomain localhost4 localhost4.localdomain4 ::1 node1 loca…...

超长上下文处理:基于Transformer上下文处理常见方法梳理
原文链接:芝士AI吃鱼 目前已经采用多种方法来增加Transformer的上下文长度,主要侧重于缓解注意力计算的二次复杂度。 例如,Transformer-XL通过缓存先前的上下文,并允许随着层数的增加线性扩展上下文。Longformer采用了一种注意力…...

ChatGPT爆火 但生成式AI并非全新产物
以ChatGPT、Midjourney 为代表的 AIGC 产品横空出世,在全球掀起新一轮的 AI 技术变革新浪潮。近二十年来,我们见证了从「机器学习」算法到「深度学习」,再到「基础模型」的发展。随着数据量大规模膨胀,可扩展的算力,再…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
