C国演义 [第五章]
第五章
- 子集
- 题目理解
- 步骤
- 树形结构
- 递归函数
- 递归结束的条件
- 单层逻辑
- 代码
- 子集II
- 题目理解
- 步骤
- 树形结构
- 递归函数
- 递归结束的条件
- 单层逻辑
- 代码
子集
力扣链接
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
- 提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同
题目理解
一看就是 回溯组合 , 那么跟 回溯组合有什么不同呢?
- 回溯组合中的, 接收结果是在叶子节点, 而这个子集是收集各个节点上的数据
步骤
树形结构

递归函数
首先, 还是两个全局变量, 一个记录单层结果, 一个记录全部结果
vector<int> path; // 记录单层结果
vector<vector<int>> result; // 记录全部结果
函数返回的类型是 void, 组合 — — startindex
void backtracking(vector<int>& nums, int startindex)
递归结束的条件
由于是要收集每个节点上的数据, 所以我们就可以不用写条件, 直接收录
result.push_back(path);
单层逻辑
单层逻辑 和 回溯组合中的 单层逻辑是一样的
for(int i = startindex; i < nums.size(); i++)
{path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();
}
代码
class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums, int startindex){result.push_back(path);for(int i = startindex; i < nums.size(); i++){path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);return result;}
};

子集II
力扣链接
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
- 提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
题目理解
哈哈, 跟上面的子集大体上是一样的, 唯一不同的是 有重复的元素 && 解集不能包含重复的子集
那么下一步的操作肯定就是 去重
步骤
树形结构
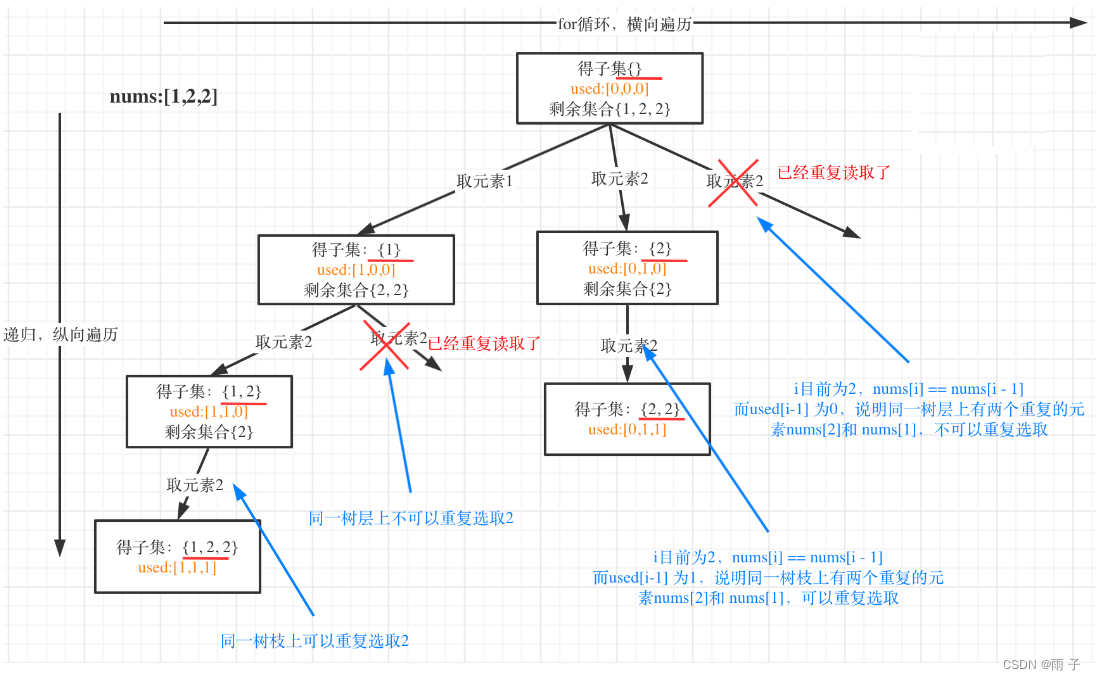
从上面的树形图可以看出:
- 同一树层上的 2 要去重 — — 树层去重
- 同一树枝上的 2 不能去重 — — 树枝不去重
- 树层去重, 树枝不去重的原因:
树层去重 — — 因为已经排序, 那么第一个 2 具有的组合 包含了后面的 2 具有的组合
树枝不去重 — — 因为 [1, 2 ] 和 [1, 2, 2] 是两个不同的结果, 一个是第一个 2, 一个是第二个 2
递归函数
首先, 还是两个全局变量, 一个记录单层结果, 一个记录全部结果
vector<int> path; // 记录单层结果
vector<vector<int>> result; // 记录全部结果
函数返回的类型是 void
组合 — — startindex
去重 — — used数组
void backtracking(vector<int>& nums, vector<bool>& used, int startindex)
递归结束的条件
由于是要收集每个节点上的数据, 所以我们就可以不用写条件, 直接收录
result.push_back(path);
单层逻辑
子集 + 去重
for(int i = startindex; i < nums.size(); i++){// 树层去重, 树枝不去重的关键if(i > 0 && ( nums[i] == nums[i - 1] ) && (used[i - 1] == false)){continue;}path.push_back(nums[i]);used[i] = true;backtracking(nums, used, i + 1);path.pop_back();used[i] = false;}
代码
class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums, vector<bool>& used, int startindex){// 子集是搜集每一个节点, 不需要结束条件result.push_back(path);for(int i = startindex; i < nums.size(); i++){// 树层去重, 树枝不去重的关键if(i > 0 && ( nums[i] == nums[i - 1] ) && (used[i - 1] == false)){continue;}path.push_back(nums[i]);used[i] = true;backtracking(nums, used, i + 1);path.pop_back();used[i] = false;}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<bool> used(nums.size(), false);sort(nums.begin(), nums.end()); // 排序很重要backtracking(nums, used, 0);return result;}
};
要人家服,只能说服,不能压服;压服的结果总是压而不服;以力服人是不行的 — — 毛泽东
相关文章:

C国演义 [第五章]
第五章 子集题目理解步骤树形结构递归函数递归结束的条件单层逻辑 代码 子集II题目理解步骤树形结构递归函数递归结束的条件单层逻辑 代码 子集 力扣链接 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。…...
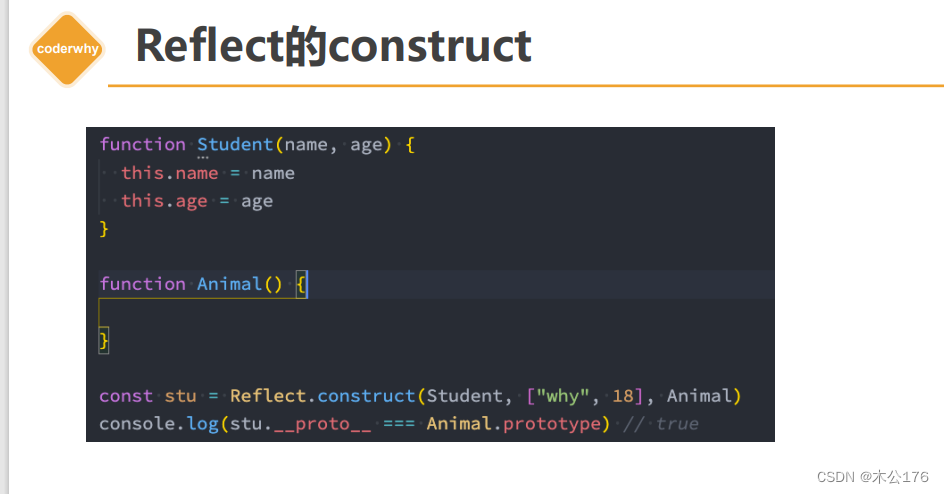
Proxy-Reflect使用详解
1 监听对象的操作 2 Proxy类基本使用 3 Proxy常见捕获器 4 Reflect介绍和作用 5 Reflect的基本使用 6 Reflect的receiver Proxy-监听对象属性的操作(ES5) 通过es5的defineProperty来给对象中的某个参数添加修改和获取时的响应式。 单独设置defineProperty是只能一次设置一…...

【Linux后端服务器开发】Shell外壳——命令行解释器
目录 一、Shell外壳概述 二、描述Shell外壳原理的生动例子 三、C语言模拟实现Shell外壳 一、Shell外壳概述 在狭义上 , 我们称Linux操作系统的内核为 Linux 在广义上 , Linux发行版 Linux内核 外壳程序 就比如市面上现在的redhat, centos, ubuntu等等我们耳熟能详的Linux发…...
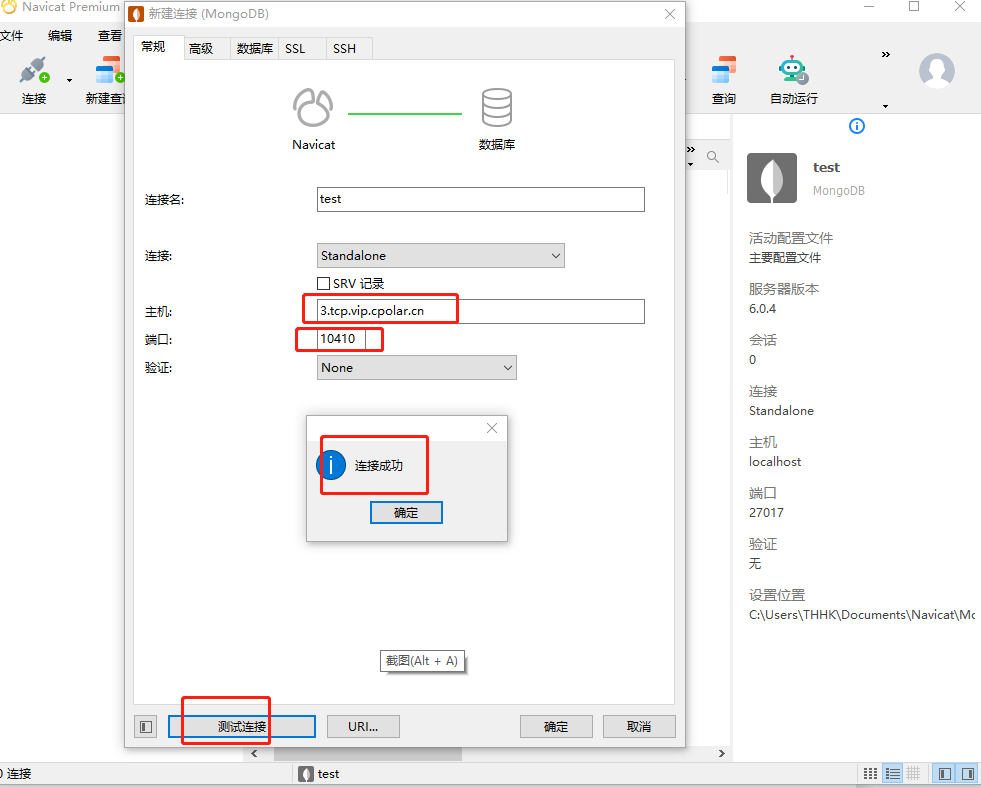
【无公网IP】在外Windows远程连接MongoDB数据库
文章目录 前言1. 安装数据库2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射2.3 测试随机公网地址远程连接 3. 配置固定TCP端口地址3.1 保留一个固定的公网TCP端口地址3.2 配置固定公网TCP端口地址3.3 测试固定地址公网远程访问 转载自cpolar极点云文章:公网远程…...

mac python3 安装virtualenv
第一步,执行安装virtualenv pip3 install virtualenv 注意:如果出现WARNING: The script virtualenv is installed in ‘/home/local/bin’ which is not on PATH. Consider adding this directory to PATH or, if you prefer to suppress this warning,…...
网络安全(自学笔记)
如果你真的想通过自学的方式入门web安全的话,那建议你看看下面这个学习路线图,具体到每个知识点学多久,怎么学,自学时间共计半年左右,亲测有效(文末有惊喜): 1、Web安全相关概念&am…...
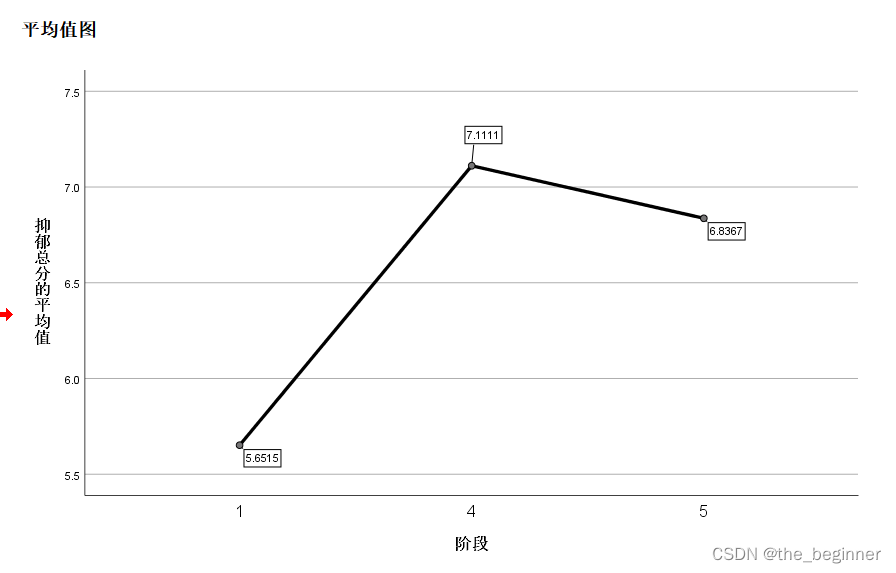
SPSS方差分析
参考文章 导入准备好的数据 选择分析方法 选择参数 选择对比,把组别放入因子框中,把红细胞增加数放进因变量列表 勾选“多项式”,等级取默认“线性” ,继续 接着点击“事后比较”,弹出对话框,勾选“LSD” …...
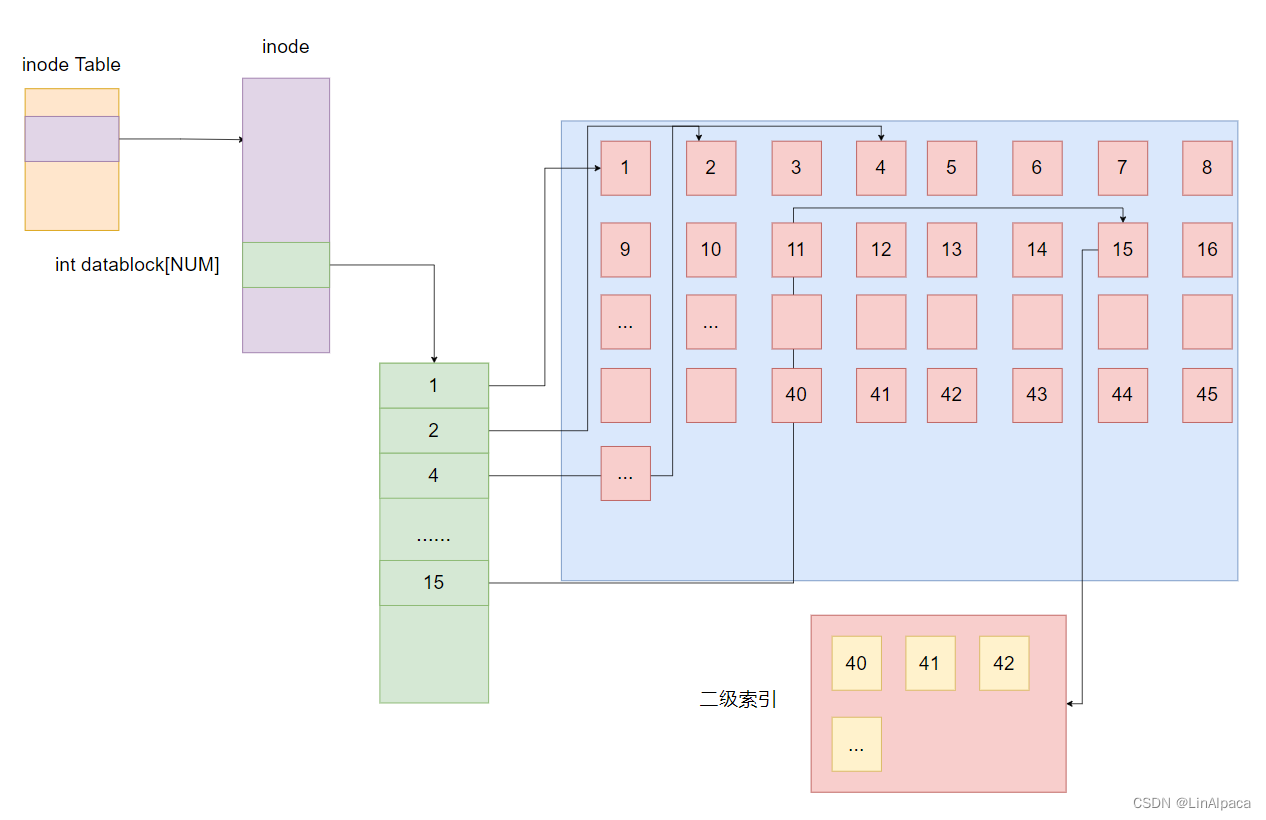
【Linux】深入理解文件系统
系列文章 收录于【Linux】文件系统 专栏 关于文件描述符与文件重定向的相关内容可以移步 文件描述符与重定向操作。 可以到 浅谈文件原理与操作 了解文件操作的系统接口。 想深入理解文件缓冲区还可以看看文件缓冲区。 目录 系列文章 磁盘 结构介绍 定位数据 抽象管理…...

12.9 专用指令
目录 状态寄存器传送指令 读CPSR 写CPSR 软中断指令 协处理器指令 协处理器数据运算指令 协处理器存储器访问指令 协处理器寄存器传送指令 伪指令 空指令 LDR 指令 伪指令 状态寄存器传送指令 专门用来读写CPSR寄存器的指令 读CPSR MRS R1,CPSR R1 CPSR 写CP…...
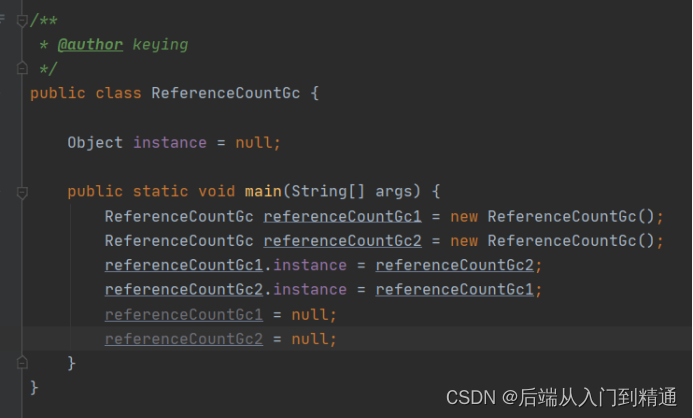
Jvm对象回收算法-JVM(九)
上篇文章介绍了jvm运行时候对象进入老年代的场景,以及如何避免频繁fullGC。 Jvm参数设置-JVM(八) 老年代分配担保机制 这个机制的目的是为了提升效率,在minorGC之前,会有三次判断,之后再次minorGC速度会…...

SpringCloud Alibaba微服务分布式架构组件演变
文章目录 1、SpringCloud版本对应1.1 技术选型依据1.2 cloud组件演变: 2、Eureka2.1 Eureka Server : 提供服务注册服务2.2 EurekaClient : 通过注册中心进行访问2.3 Eureka自我保护 3、Eureka、Zookeeper、Consul三个注册中心的异同点3.1 CP…...
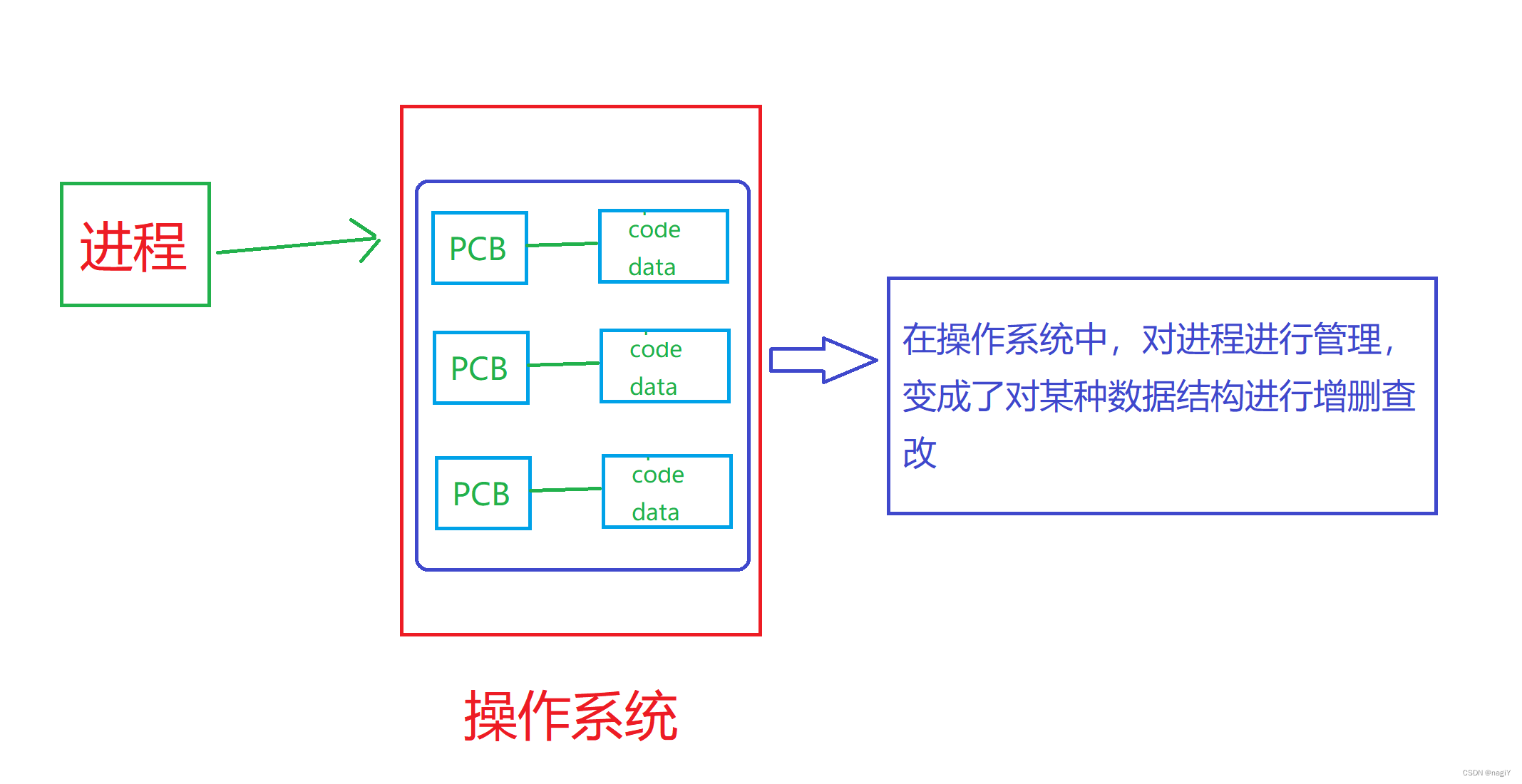
【Linux】初步理解操作系统和进程概念
一.认识操作系统 操作系统是一款纯正的 “搞管理” 的文件。 那操作系统为什么要管理文件? “管理” 又是什么? 它是怎么管理的? 为什么? 1.操作系统帮助用户,管理好底层的软硬件资源; 2.为了给用户提供一个…...

TypeScript 中的字面量类型和联合类型特性
字面量类型和联合类型是 TypeScript 中常用的类型特性。 1. 字面量类型: 字面量类型是指具体的值作为类型。例如,字符串字面量类型可以通过给定的字符串字面量来限制变量的取值范围。 let status: "success" | "error"; // status…...

react+jest+enzyme配置及编写前端单元测试UT
文章目录 安装及配置enzyme渲染测试技巧一、常见测试二、触发ant design组件三、使用redux组件四、使用路由的组件五、mock接口网络请求六、mock不需要的子组件 安装及配置 安装相关库: 首先,使用npm或yarn安装所需的库。 npm install --save-dev jest…...
自学网络安全(黑客)
一、为什么选择网络安全? 这几年随着我国《国家网络空间安全战略》《网络安全法》《网络安全等级保护2.0》等一系列政策/法规/标准的持续落地,网络安全行业地位、薪资随之水涨船高。 未来3-5年,是安全行业的黄金发展期,提前踏入…...

【unity小技巧】委托(Delegate)的基础使用和介绍
文章目录 一、前言1. 什么是委托?2. 使用委托的优点 二、举例说明1. 例12. 例2 三、案例四、泛型委托Action和Func1. Action委托2. Func委托 五、参考六、完结 一、前言 1. 什么是委托? 在Unity中,委托(Delegate)是一…...
)
【MySQL必知必会】第24章 使用游标(学习笔记)
游标 游标(cursor)是一个存储在MySQL服务器上的数据库查询,它不是一条select语句,而是被该语句检索出来的结果集游标主要用于交互式应用,其中用户需要滚动屏幕上的数据,并对数据进行浏览或做出更改只能用于存储过程,不…...

rosbag回放指定话题外的其他话题的方法
假设要回放file.bag包中除/tf话题外的所有话题 方法一 将原本/tf话题转发到另一个“黑洞话题”去,这样/tf话题就没输出了 rosbag play file.bag /tf:/tf_dev_null方法二 使用filter选项,重新生产一个新的不含/tf话题的包 rosbag filter file.bag fi…...
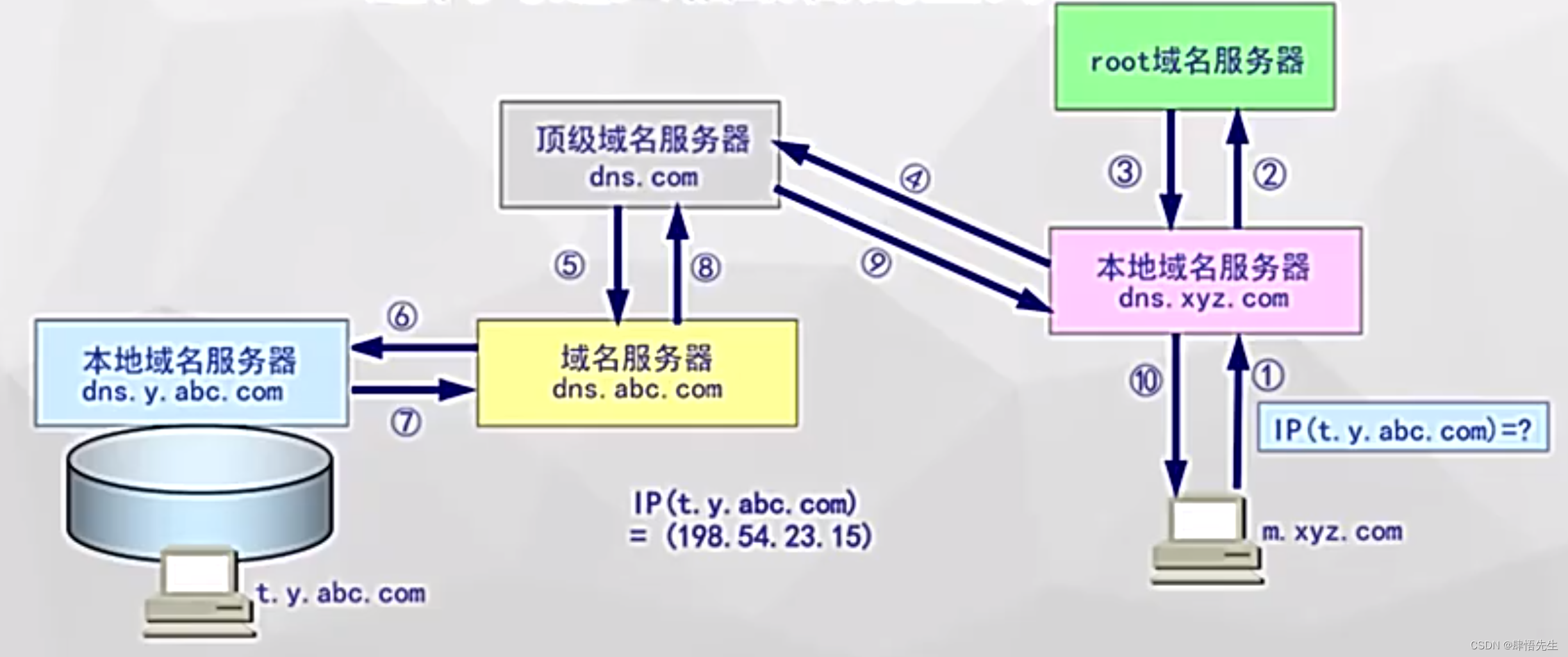
6.2.1 网络基本服务---域名解析系统DNS
6.2.1 网络基本服务—域名解析系统DNS 因特网是需要提供一些最基本的服务的,今天我们就来讨论一下这些基本的服务。 域名系统(DNS)远程登录(Telnet)文件传输协议(FTP)动态主机配置协议&#x…...
通用文字识别OCR 之实现自动化办公
摘要 随着技术的发展,通用文字识别(OCR)已经成为现代办公环境中不可或缺的工具之一。OCR技术可以将印刷或手写文本转换为可编辑或可搜索的数字文本,极大地提高了办公效率并实现了自动化办公。本文将深入探讨OCR技术在实现自动化办…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
